PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Hàm số $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên khoảng $K$ nếu

A. $F'(x) = -f(x), \forall x \in K$.

B. $f'(x) = F(x), \forall x \in K$.

C. $f'(x) = -F(x), \forall x \in K$.

D. $F'(x) = f(x), \forall x \in K$.

Câu 2: Hàm số $F(x)$ là nguyên hàm của hàm số $f(x) = 3x^2$ và $F(0) = 5$. Khi đó, hàm số $F(x)$ là

A. $F(x) = x^3 + 5$.

B. $F(x) = x^3 – 5$.

C. $F(x) = 3x^3 + 5$.

D. $F(x) = 6x + 5$.

Câu 3: Cho hàm số $y = f(x)$ có đạo hàm liên tục trên $[0; 2]$, $f(0) = 1$ và $\int_0^2 f'(x) dx = -3$. Tính $f(2)$?

A. $f(2) = -4$.

B. $f(2) = 4$.

C. $f(2) = -2$.

D. $f(2) = -3$.

Câu 4: Biết $F(x) = x^3$ là một nguyên hàm của hàm số $f(x)$ trên $\mathbb{R}$. Giá trị của $\int_0^2 [-4 + f(x)] dx$ bằng

A. $0$.

B. $-4$.

C. $12$.

D. $2$.

Câu 5: Tính tích phân $\int_0^1 e^{3x+1} dx$ bằng

A. $\frac{1}{3}(e^4 + e)$.

B. $e^3 – e$.

C. $\frac{1}{3}(e^4 – e)$.

D. $e^4 – e$.

Câu 6: Tính tích phân $I = \int_0^{\frac{\pi}{4}} 2 \sin x dx$.

A. $I = 7$.

B. $I = 5 + \frac{\pi}{2}$.

C. $I = 3$.

D. $I = 2$.

Câu 7: Cho hàm số $y = f(x)$ xác định và liên tục trên đoạn $[a; b]$. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$, trục hoành và hai đường thẳng $x = a, x = b$ được tính theo công thức

A. $S = \int_a^b |f(x)| dx$.

B. $S = \int_a^b f(x) dx$.

C. $S = -\int_a^b f(x) dx$.

D. $S = \int_b^a |f(x)| dx$.

Câu 8: Diện tích $S$ của hình phẳng giới hạn bởi các đường $y = 2x^2$, $y = -1$, $x = 0$ và $x = 1$ được tính bởi công thức nào sau đây?

A. $S = \pi \int_0^1 (2x^2 + 1) dx$.

B. $S = \int_0^1 (2x^2 – 1) dx$.

C. $S = \int_0^1 (2x^2 + 1)^2 dx$.

D. $S = \int_0^1 (2x^2 + 1) dx$.

Câu 9: Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $(P): x – 2y + 3z – 1 = 0$. Vector nào dưới đây là một vector pháp tuyến của $(P)$?

A. $\vec{n_1} = (1; 3; -1)$.

B. $\vec{n_2} = (-2; 3; -1)$.

C. $\vec{n_3} = (1; -2; -1)$.

D. $\vec{n_4} = (1; -2; 3)$.

Câu 10: Trong không gian với hệ tọa độ $Oxyz$, phương trình nào dưới đây là phương trình mặt phẳng đi qua điểm $A(1; 2; -3)$ và có vector pháp tuyến $\vec{n} = (1; -2; 3)$?

A. $x – 2y + 3z – 12 = 0$.

B. $x – 2y – 3z + 6 = 0$.

C. $x – 2y + 3z + 12 = 0$.

D. $x – 2y – 3z – 6 = 0$.

Câu 11: Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d: \frac{x-2}{-1} = \frac{y-1}{2} = \frac{z+3}{1}$. Vector nào dưới đây là một vector chỉ phương của $d$?

A. $\vec{u_1} = (2; 1; -3)$.

B. $\vec{u_2} = (-2; -1; 3)$.

C. $\vec{u_3} = (-1; 2; 1)$.

D. $\vec{u_4} = (-1; 2; -1)$.

Câu 12: Trong không gian với hệ tọa độ $Oxyz$, cho bốn điểm $A(-2; 6; 3)$, $B(1; 0; 6)$, $C(0; 2; -1)$, $D(1; 4; 0)$. Phương trình nào dưới đây là phương trình mặt phẳng $(\alpha)$ chứa $AB$ và song song với $CD$?

A. $-x + z + 5 = 0$.

B. $x – 2y + z + 11 = 0$.

C. $x – z + 5 = 0$.

D. $x – 2y + z – 7 = 0$.

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Một viên đạn được bắn thẳng đứng lên trên từ độ cao $2m$ so với mặt đất (coi $t = 0$ giây là thời điểm viên đạn được bắn lên), vận tốc của viên đạn được cho bởi công thức $v(t) = 60 – 10t(m/s)$.

a) Vận tốc của viên đạn tại thời điểm $t = 2$ giây bằng $40(m/s)$.

b) Viên đạn đạt độ cao lớn nhất sau 6 giây.

c) Độ cao của viên đạn tại thời điểm $t$ được xác định bởi công thức $h(t) = 60t – 5t^2$.

d) Độ cao lớn nhất của viên đạn so với mặt đất là 180 (m).

Câu 2. Gọi $(H)$ là hình phẳng giới hạn bởi đồ thị hai hàm số $f(x) = x^2 – 2x + 2$ và $g(x) = x + 2$.

a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = g(x)$ các đường thẳng $x = -1; x = 1$, trục $Ox$ bằng 4.

b) Hoành độ giao điểm của đồ thị hai hàm số $y = f(x)$ và $y = g(x)$ là $x = 0; x = 3$.

c) Hình $(H)$ có diện tích bằng $\frac{2}{3}$.

d) Thể tích khối tròn xoay khi quay hình $(H)$ quanh trục $Ox$ bằng $\frac{117}{5}$.

Câu 3. Cho hình phẳng $(S)$ giới hạn bởi đồ thị hàm số $y = f(x) = \sqrt{25 – x^2}$, trục hoành và hai đường thẳng $x = -5, x = 5$.

a) Đạo hàm của hàm số $f(x)$ bằng $\frac{x}{\sqrt{25 – x^2}}$.

b) Diện tích hình phẳng $(S)$ bằng $25\pi$.

c) Thể tích của khối tròn xoay khi quay $(S)$ quanh $Ox$ là $\frac{500}{3}\pi$.

d) Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$ và đường thẳng $y = 3$ bằng $K = 2\int_0^4 \sqrt{25 – x^2} dx – 12$.

Câu 4. Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(1; -3; 0), B(-5; 1; 2)$. Gọi $(P)$ là mặt phẳng trung trực của đoạn thẳng $AB$. Xét tính đúng sai của các mệnh đề sau

a) $\overrightarrow{AB} = (6; -4; -2)$.

b) Một vector pháp tuyến của mặt phẳng $(P)$ là $\vec{n} = (12; -8; -4)$.

c) Phương trình mặt phẳng $(P)$ là: $-3x + 2y + z – 3 = 0$.

d) Gọi $(Q)$ là mặt phẳng đi qua $C(1; -3; 9)$ và song song với $(P)$ thì mặt phẳng $(Q)$ đi qua gốc tọa độ.

PHẦN III. Câu trắc nghiệm trả lời ngắn.

Thí sinh trả lời từ câu 1 đến câu 6. Ở mỗi câu thí sinh điền đáp án của câu đó.

Câu 1: Nhằm trị ăn người dân địa phương đã luôn tìn tưởng, đồng hành với doanh nghiệp, tập đoàn X đã tổ chức ngày hội cảm ơn vào ngày 10/07/2024. Gọi $B(t)$ là hàm số biểu thị số lượng khách tham quan sau $t$ giờ mở cửa. Khi đó tốc độ thay đổi lượng khách tham quan trong ngày được biểu diễn bằng hàm số $B'(t) = 4t^3 – 3t^2 + 200$ trong đó $t$ tính bằng giờ $(0 \leq t \leq 8)$, $B'(t)$ tính bằng khách/giờ. Sau 2 giờ đã có 1200 người có mặt. Hỏi sau 6 giờ lượng khách tham quan là bao nhiều người?

Câu 2: Một chiếc xe chuyển động với đồ thị vận tốc được biểu diễn theo đường gấp khúc được minh họa trên hệ trục $Otv$ như hình vẽ (mỗi đơn vị trên $Ot$ ứng với 1 phút và mỗi đơn vị trên $Ov$ ứng với $0,4 km/$ phút).

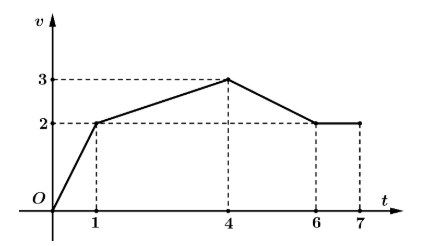
Quãng đường mà xe đã đi chuyển trong 7 phút là bao nhiều km?

Câu 3: Một ô tô đang chạy với vận tốc 54(km/h) thì thay đổi vận tốc với gia tốc được tính theo thời gian là $a(t) = -6 + 2t(m/s^2)$. Tính quãng đường xe ô tô đi được trong khoảng thời gian 3 giây kể từ lúc ô tô bắt đầu tăng tốc (đơn vị là m).

Câu 4: Người ta dự định làm cổng vào một khu tham quan du lịch có dạng parabol với chiều cao bằng $4m$ và đáy $AB = 4m$. Trong đó, phần cửa đi được thiết kế là hình chữ nhật $CDEF$ với $C, F$ thuộc đoạn thẳng $AB$ và $D, E$ thuộc parabol (tham khảo hình vẽ bên dưới). Biết chi phí phần cửa đi là 2 triệu đồng/m² và phần còn lại là 3 triệu đồng/m². Hỏi cần ít nhất bao nhiều triệu đồng để hoàn thành công (làm tròn đến hàng phần mười)?

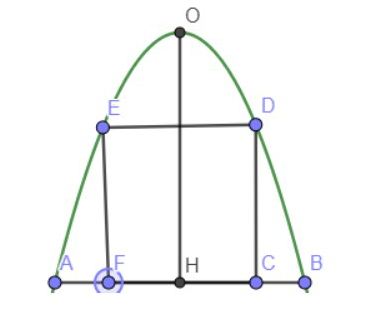
Câu 5: Trong không gian $Oxyz$, cho hai điểm $A(1; 3; 0)$, $B(3; 1; 0)$ và mặt phẳng $(P): x – y + z + 5 = 0$. Mặt phẳng $(Q)$ song song với mặt phẳng $(P)$ và cách đều hai điểm $A; B$ có dạng $x + by + cz + d = 0$. Tính $b + c + d$.

Câu 6: Một phần mềm mô phỏng vận động viên tập bắn bia mục tiêu có kích thước nhỏ $(42 \times 42cm)$ bằng súng tiểu liên AK trong không gian $Oxyz$. Cho biết vận động viên đỗ sử dụng thước ngắm 3 và đứng cách xa bia mục tiêu là $100m$, trục $d$ của nòng súng và cọc đỗ bia $d’$ lần lượt có phương trình

$d: \begin{cases} x = t \ y = 2 \ z = 4 \end{cases}$ và $d’: \begin{cases} x = 1 \ y = 2 \ z = 1 + 3t \end{cases}$. Để bắn trúng hồng tâm (điểm 10) thì vận động viên phải ngắm bắn vào điểm $N(a; b; c) \in d’$ và cách giao điểm của $d$ và $d’$ một khoảng $6cm$. Khi $c < 0$, tính giá trị biểu thức $a – b + c$.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh