PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: Hàm số $F(x)$ có đạo hàm trên $\mathbb{R}$ là hàm số $f(x)$. Khẳng định nào dưới đây đúng?

A. $\int f(x)dx = F(x) + C$.

B. $\int f(x)dx = F'(x) + C$.

C. $\int F'(x)dx = f(x) + C$.

D. $\int F(x)dx = f(x) + C$.

Câu 2: Biết $\int f(x)dx = \frac{5^x}{\ln 5} + 3x + C$. Khi đó $f(x)$ bằng

A. $f(x) = \frac{5^x}{\ln 5} + 3$.

B. $f(x) = \frac{5^x}{\ln 5} + 3x$.

C. $f(x) = 5^x + 3x$.

D. $5^x + 3$.

Câu 3: Cho hàm số $f(x)$ có đạo hàm trên đoạn $[1; 2025]$, $f(1) = 1$ và $f(2025) = 2$. Tích phân $I = \int_1^{2025} f'(x)dx$ bằng

A. $2025$.

B. $1$.

C. $2024$.

D. $2$.

Câu 4: Nếu $\int_2^5 f(x)dx = 3$ thì $\int_2^5 -4f(x)dx$ bằng

A. $-12$.

B. $4$.

C. $12$.

D. $3$.

Câu 5: Biết $\int_0^1 (x^4 – 2x^2 + 3)dx = \frac{a}{b}$ với $a, b \in \mathbb{R}, b \neq 0$ và $\frac{a}{b}$ là phân số tối giản. Tính $T = a + b$.

A. $34$.

B. $53$.

C. $45$.

D. $35$.

Câu 6: Tính $\int_0^{\pi} (3 – \cos x)dx$.

A. $\frac{\pi}{2} – 1$.

B. $\frac{\pi + 1}{2}$.

C. $\frac{\pi – \sqrt{3}}{2}$.

D. $\frac{\pi – 1}{2}$.

Câu 7: Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = x – x^2$, trục hoành và hai đường thẳng $x = -1$, $x = 2$ là

A. $S = \int_{-1}^2 |x – x^2| dx$.

B. $S = \int_{-1}^2 (x – x^2) dx$.

C. $S = \int_{-1}^2 (x^2 – x) dx$.

D. $S = \left|\int_{-1}^2 (x – x^2) dx\right|$.

Câu 8: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = x^3 – 4x$, trục hoành và hai đường thẳng $x = 0; x = 3$.

A. $S = \frac{9}{4}$.

B. $S = \frac{25}{4}$.

C. $S = \frac{41}{4}$.

D. $S = 11$.

Câu 9: Trong không gian với hệ tọa độ $Oxyz$, cho mặt phẳng $(P)$ có phương trình $(P): \frac{x}{2} + \frac{y}{-3} + \frac{z}{6} = 1$. Một véc tơ pháp tuyến của mặt phẳng $(P)$ là

A. $\vec{n} = (2; 3; 6)$.

B. $\vec{n} = \left(\frac{1}{2}; \frac{1}{3}; \frac{1}{6}\right)$.

C. $\vec{n} = (2; -3; 6)$.

D. $\vec{n} = \left(\frac{1}{2}; -\frac{1}{3}; \frac{1}{6}\right)$.

Câu 10: Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A(2; 3; 2), B(0; 1; 4)$, mặt phẳng trung trực của đoạn $AB$ có phương trình là

A. $(P): x + y – z = 0$.

B. $(P): x + y – z + 1 = 0$.

C. $(P): -2x – 2y + 2z + 1 = 0$.

D. $(P): -2x – 2y + 2z + 2 = 0$.

Câu 11: Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $(d)$ có phương trình tham số $(d): \begin{cases} x = -t \ y = 1 \ z = 2 + 3t \end{cases}, t \in \mathbb{R}$. Một véc tơ chỉ phương của đường thẳng $(d)$ là

A. $\vec{u} = (-1; 1; 2)$.

B. $\vec{u} = (-1; 1; 3)$.

C. $\vec{u} = (-1; 0; 2)$.

D. $\vec{u} = (-1; 0; 3)$.

Câu 12: Trong không gian với hệ tọa độ $Oxyz$, phương trình chính tắc của đường thẳng $(d)$ đi qua điểm $M(1; -2; 3)$ và vuông góc với mặt phẳng $(P): x – 2y + 3z – 1 = 0$ là

A. $\frac{x – 1}{1} = \frac{y + 2}{-2} = \frac{z + 3}{3}$.

B. $\frac{x – 1}{1} = \frac{y + 2}{-2} = \frac{z – 3}{3}$.

C. $\frac{x + 1}{1} = \frac{y + 2}{-2} = \frac{z – 3}{3}$.

D. $\frac{x – 1}{1} = \frac{y – 2}{-2} = \frac{z – 3}{3}$.

PHẦN II. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1: Cho hàm số $f(x) = 5$ và hàm số $g(x) = \sin x$.

a) $\int f(x)dx = 5x + C$.

b) $\int [f(x) + g(x)]dx = 5x + \cos x + C_1$.

c) Gọi $G(x)$ là một nguyên hàm của $g(x)$. Biết $G(x) = 3$ thì $G(x) = -\cos x + 2$.

d) Gọi $F(x)$ là một nguyên hàm của $f(x)$. Biết $F(1) = 3$ thì $F(1) + F(2) + … + F(100) = 25560$.

Câu 2: Cho các hàm số $f(x)$ và $F(x)$ liên tục trên $\mathbb{R}$ thỏa $F'(x) = f(x), \forall x \in \mathbb{R}$.

a) $\int_a^b f(x)dx = F(b) – F(a)$.

b) $\int_{2025}^{2025} f(x)dx = 2025$.

c) Nếu $F(0) = 2, F(1) = 8$. Khi đó: $\int_0^1 f(x)dx = -6$.

d) Cho $f(x) = 3^x$ và $\int_0^a f(x)dx = \frac{a}{\ln 3}$. Khi đó $a = 8$.

Câu 3: Trong không gian $Oxyz$, cho mặt phẳng $(P): 2x – y + 2z – 8 = 0$.

a) Điểm $M(2; -1; 2)$ thuộc mặt phẳng $(P)$.

b) Tọa độ một vector pháp tuyến của mặt phẳng $(P)$ là $\vec{n} = (2; -1; 2)$.

c) Mặt phẳng $(Q)$ đi qua điểm $A(3; 2; -1)$ và song song với mặt phẳng $(P)$ có phương trình là $2x – y + 2z – 2 = 0$.

d) Gọi $(R)$ là mặt phẳng vuông góc với mặt phẳng $(P)$ và mặt phẳng $(Oxy)$, đồng thời cách điểm $B(-3; 1; 5)$ một khoảng bằng $\sqrt{5}$. Giả sử $(R)$ có phương trình $ax + by + d = 0, (a > 0, d < 0)$, $a, b \in \mathbb{R}, (a, b) = 1$. Giá trị của biểu thức $b + d = -4$.

Câu 4: Trong không gian $Oxyz$, cho hai điểm $M(1; -1; 0), N(-2; 0; 4)$.

a) Tọa độ một vector chỉ phương của đường thẳng $MN$ là $\vec{d} = (-3; 1; 4)$.

b) Phương trình chính tắc của đường thẳng $MN$ là $\frac{x – 1}{3} = \frac{y + 1}{-1} = \frac{z}{-4}$.

c) Đường thẳng $MN$ và đường thẳng $d: \begin{cases} x = -5 + 3t \ y = 1 – t \ z = 8 – 4t \end{cases}$ song song với nhau.

d) Gọi $\alpha$ là góc giữa đường thẳng $MN$ và trục $Ox$. Khi đó $\sin \alpha = \frac{3\sqrt{26}}{26}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn (Tự luận).

Thí sinh trả lời từ câu 1 đến câu 6. Ở mỗi câu thí sinh điền đáp án của câu đó.

Câu 5: Một chiếc cốc chứa nước ở $95°C$ được đặt trong phòng có nhiệt độ $20°C$. Theo định luật làm mát của Newton, nhiệt độ của nước trong cốc sau $t$ phút (xem $t = 0$ là thời điểm nước ở $95°C$) là một hàm số $T(t)$. Tốc độ giảm nhiệt độ của nước trong cốc tại thời điểm $t$ phút được xác định bởi $T'(t) = -\frac{3}{2}e^{-\frac{t}{20}}$ (°C/phút). Nhiệt độ của nước tại thời điểm $t = 20$ phút bằng bao nhiều độ C? (Kết quả làm tròn đến hàng phần chục)

(nguồn: https://amsi.org.au/ESA_Senior_Years/SeniorTopic3/3e/3e_4history_3.html).

Câu 6: Biết $\int_1^e \frac{1}{x^3 + x} dx = a \ln(e^2 + 1) + b \ln 2 + c$, với $a$, $b$, $c$ là các số hữu tỉ. Tính $S = a + b + c$.

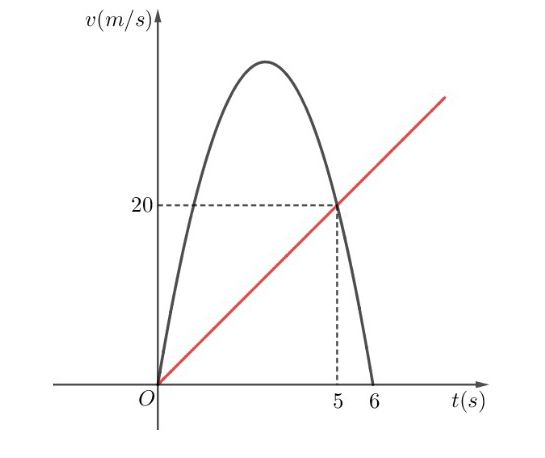
Câu 7: Cho đồ thị biểu diễn vận tốc của 2 chất điểm $A$ và $B$ bắt đầu chuyển động cùng một lúc và cùng vạch xuất phát, cùng chiều trên một con đường. Biết đồ thị biểu diễn vận tốc của chất điểm $A$ là một đường parabol và đồ thị biểu diễn vận tốc của chất điểm $B$ là một đường thẳng như hình vẽ.

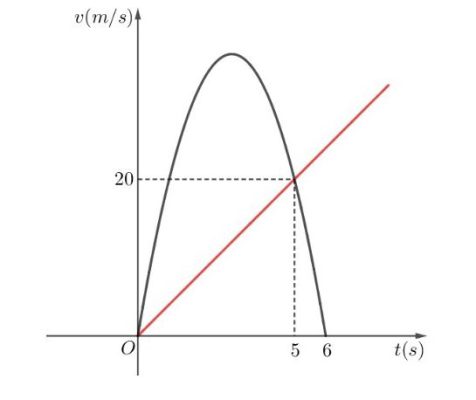
Hỏi sau 8 giây kể từ lúc xuất phát thì khoảng cách giữa hai chất điểm là bao nhiều mét?

(Biết rằng chất điểm $A$ sẽ dừng lại khi vận tốc bằng $0$).

Câu 8: Vào buổi học cuối cùng trước khi học sinh của mình bước vào kì thi Tốt nghiệp trung học phổ thông, Thầy Vinh đã trang trí bảng bằng một câu chúc thật ý nghĩa là “ĐỖ NV1” và đầm chất toán học.

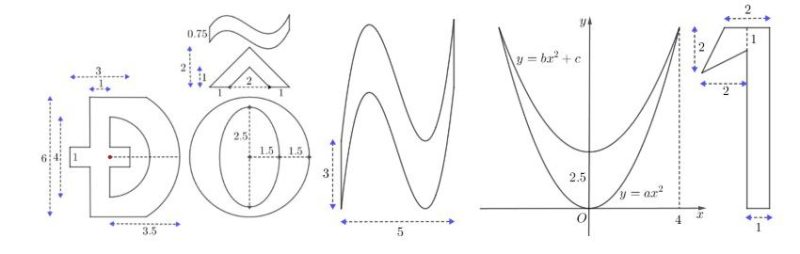
Sau đó để tạo không khí thật vui vẻ, Thầy đã đố cả lớp chữ $V$ trên bảng có diện tích bao nhiêu.

Ai đoán đúng sẽ nhận được phần thưởng là diện tích chữ $V$ nhân với $10.000$ đồng. Hỏi tiền thưởng là bao nhiêu ngàn đồng (làm tròn đến hàng đơn vị)?

Câu 9: Trong không gian với hệ tọa độ $Oxyz$, cho 3 điểm $A(0, 0, 3); B(1, 1, 3); C(0, 1, 1)$. Khoảng cách từ góc tọa độ $O$ đến mặt phẳng $(ABC)$ bằng?

Câu 10: Trong giải đoạn sửa chữa cầu, nhà thầu thi công gia có thêm hệ thống chịu tải là 2 thanh sắt có độ dài bằng nhau (được vẽ nét đứt trong hình)

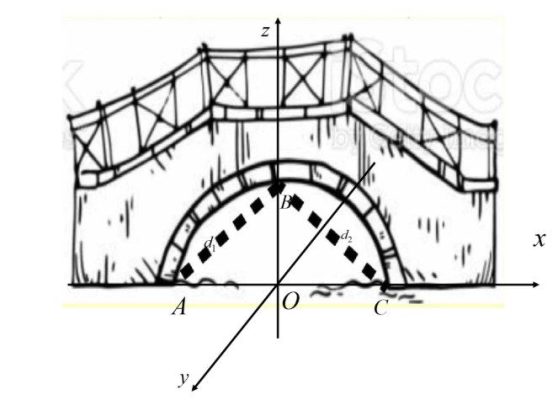
Biết phần cong của dây cầu là nửa đường cong bán kính 2m. Với hệ trục tọa độ như hình vẽ ta có phương trình đường thẳng của những thanh chịu tải là $d_1 \begin{cases} x = mt \ y = 0 \ z = 2 + t \end{cases}$ và $d_2 \begin{cases} x = nt \ y = 0 \ z = 2 + t \end{cases}$ (với $m, n \in \mathbb{R}$).

Xác định $m + n$.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh