PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1: [NB] Cho hàm số $f(x)$ xác định trên khoảng $K$. Hàm số $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên khoảng $K$ nếu

A. $F'(x) = -f(x), \forall x \in K$.

B. $f'(x) = F(x), \forall x \in K$.

C. $F'(x) = f(x), \forall x \in K$.

D. $f'(x) = -F(x), \forall x \in K$.

Câu 2: [NB] Họ tất cả các nguyên hàm của $f(x) = \cos x + \sin x$ là

A. $\sin x + \cos x + C$.

B. $\sin x – \cos x$.

C. $\sin x – \cos x + C$.

D. $-\sin x + \cos x + C$.

Câu 3: [NB] Cho $f(x)$ là hàm số liên tục trên đoạn $[a; b]$ và $F(x)$ là một nguyên hàm của hàm số $f(x)$ trên đoạn $[a; b]$. Tích phân từ $a$ đến $b$ của hàm số $f(x)$ được kí hiệu là

A. $\int_a^b F(x)dx = f(x)\Big|_a^b = f(a) – f(b)$.

B. $\int_a^b f(x)dx = F(x)\Big|_a^b = F(a) – F(b)$.

C. $\int_a^b F(x)dx = f(x)\Big|_a^b = f(b) – f(a)$.

D. $\int_a^b f(x)dx = F(x)\Big|_a^b = F(b) – F(a)$.

Câu 4: [NB] Cho hàm số $f(x), g(x)$ liên tục trên đoạn $[a; b]$. Mệnh đề nào sau đây sai?

A. $\int_a^b kf(x)dx = k\int_a^b f(x)dx$ ($k$ là hằng số).

B. $\int_a^b [f(x) + g(x)]dx = \int_a^b f(x)dx + \int_a^b g(x)dx$.

C. $\int_a^b [f(x).g(x)]dx = \int_a^b f(x)dx \int_a^b g(x)dx$.

D. $\int_a^b f(x)dx = \int_a^c f(x)dx + \int_c^b f(x)dx$ $(a < c < b)$.

Câu 5: [Mức độ 2] Tích phân $\int_1^3 x^2 dx$ bằng

A. $15$.

B. $20$.

C. $30$.

D. $28$.

Câu 6: [Mức độ 1] Tích phân $\int_0^{\frac{\pi}{2}} \cos x dx$ bằng

A. $-1$.

B. $0$.

C. $1$.

D. $2$.

Câu 7: [Mức độ 1] Cho hàm số $y = f(x)$ liên tục trên $[a; b]$. Gọi $D$ là miền hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$, trục hoành và các đường thẳng $x = a$, $x = b(a < b)$. Diện tích của $D$ được cho bởi công thức nào sau đây?

A. $S = \int_a^b |f(x)|dx$.

B. $\int_a^b f(x)dx$.

C. $S = \int_a^b f(x)dx$.

D. $S = \pi \int_a^b f^2(x)dx$.

Câu 8: [Mức độ 2] Diện tích hình phẳng giới hạn bởi các đường $y = x^3 – 6x$ và $y = x^2$ bằng

A. $\frac{125}{12}$.

B. $\frac{253}{12}$.

C. $\frac{63}{4}$.

D. $\frac{16}{3}$.

Câu 9: [Mức độ 2] Trong không gian $Oxyz$ khoảng cách giữa hai mặt phẳng $(P): x + 2y + 3z – 1 = 0$ và $(Q): x + 2y + 3z + 6 = 0$ là

A. $\frac{7}{\sqrt{14}}$.

B. $\frac{8}{\sqrt{14}}$.

C. $14$.

D. $\frac{5}{\sqrt{14}}$.

Câu 10: [Mức độ 2] Trong không gian với hệ tọa độ $Oxyz$, mặt phẳng đi qua ba điểm $A(2; 3; 5)$, $B(3; 2; 4)$ và $C(4; 1; 2)$ có phương trình là

A. $3x – y + 2z – 4 = 0$.

B. $x + y – 5 = 0$.

C. $y – z + 2 = 0$.

D. $2x + y – 7 = 0$.

Câu 11: [Mức độ 1] Trong không gian $Oxyz$, đường thẳng $d: \begin{cases} x = 2 – t \ y = -1 + 2t \ z = 3 + 3t \end{cases}$ có một vector chỉ phương là:

A. $\vec{u_1} = (2; -1; 3)$.

B. $\vec{u_2} = (-1; 2; 3)$.

C. $\vec{u_3} = (2; 1; 3)$.

D. $\vec{u_4} = (1; 2; 3)$.

Câu 12: [Mức độ 1] Trong không gian $Oxyz$, cho hai điểm $M(1; 0; 1)$ và $N(2; 1; 0)$. Đường thẳng $MN$ có phương trình tham số là

A. $\begin{cases} x = 1 + 2t \ y = 2t \ z = 1 + t \end{cases}$

B. $\begin{cases} x = 1 + t \ y = t \ z = 1 + t \end{cases}$

C. $\begin{cases} x = 1 – t \ y = t \ z = 1 + t \end{cases}$

D. $\begin{cases} x = 1 + t \ y = t \ z = 1 – t \end{cases}$

PHẦN II. Câu trắc nghiệm đúng sai.

Câu 1: Một ô tô đang chạy với tốc độ $72 km/h$ thì người lái xe bắt ngờ phát hiện chướng ngại vật trên đường. Người lái xe phản ứng một giây sau đó bằng cách đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ $v(t) = -10t + 30 (m/s)$, trong đó $t$ là thời gian tính bằng giây kể từ lúc đạp phanh. Gọi $s(t)$ là quãng đường xe ô tô đi được trong $t(s)$ kể từ lúc đạp phanh.

a) Công thức biểu diễn hàm số $s(t) = -5t^2 + 30t + 72 (m)$.

b) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là $3$ giây.

c) Sau 3 giây kể từ lúc đạp phanh, quãng đường xe ô tô đi chuyển được là $45 (m)$.

d) Quãng đường xe ô tô đã đi chuyển kể từ lúc người lái xe phát hiện chướng ngại vật trên đường đến khi xe ô tô dừng hẳn là $120 (m)$.

Câu 2: Giả sử lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức $P'(x) = -0,0008x + 10,4$. Ở đây $P(x)$ là lợi nhuận (tính bằng triệu đồng) khi bán được $x$ đơn vị sản phẩm.

a) Lợi nhuận khi bán được $x$ đơn vị sản phẩm được tính bằng công thức $P(x) = -0,0008x^2 + 10,4x$.

b) Lợi nhuận khi bán được $50$ sản phẩm đầu tiên là $519$ triệu đồng.

c) Sự thay đổi của lợi nhuận khi doanh số tăng từ $50$ lên $55$ đơn vị sản phẩm là $49,79$ triệu đồng.

d) Biết sự thay đổi của lợi nhuận khi doanh số tăng từ $50$ lên $a$ đơn vị sản phẩm lớn hơn $517$ triệu đồng, khi đó giá trị nhỏ nhất của $a$ là $100$.

Câu 3: Trong không gian $Oxyz$, cho điểm $A(1; 2; 3), B(2; -3; 1)$ và mặt phẳng $(P): 2x – y + 2z + 5 = 0$. Các khẳng định sau đúng hay sai?

a) Một vector pháp tuyến của mặt phẳng $(P)$ là $\vec{n} = (2; -1; 2)$.

b) Khoảng cách từ điểm $A$ đến mặt phẳng $(P)$ bằng $2$.

c) Phương trình mặt phẳng $(Q)$ đi qua $A$ và song song với mặt phẳng $(P)$ có phương trình là: $2x – y + 2z + 6 = 0$.

d) Giả sử điểm $M(a; b; c)$ thuộc mặt phẳng $(Oxy)$ sao cho $MA + MB$ ngắn nhất. Khi đó tổng $a – b + 2c = \frac{7}{2}$.

Câu 4: Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A(1; 2; -1)$, đường thẳng $d: \begin{cases} x = 3 + t \ y = 3 + 3t, (t \in \mathbb{R}) \ z = 2t \end{cases}$ và mặt phẳng $(P): x + y – z + 3 = 0$. Các khẳng định sau đúng hay sai?

a) Một vector chỉ phương của đường thẳng $(d)$ là $\vec{u} = (1; 3; 2)$.

b) Đường thẳng đi qua $A$ và vuông góc với $(P)$ có phương trình chính tắc là $\frac{x + 1}{1} = \frac{y + 2}{1} = \frac{z – 1}{-1}$.

c) Giả sử $M(a; b; c)$ là giao điểm của đường thẳng $d$ và mặt phẳng $(P)$. Khi đó $a + b + c = 21$.

d) Đường thẳng $(\Delta)$ đi qua $A$, cắt $d$ tại điểm $B$ và song song với mặt phẳng $(P)$. Độ dài đoạn thẳng $AB = \sqrt{6}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn (Tự luận).

Thí sinh trả lời từ câu 1 đến câu 6. Ở mỗi câu thí sinh điền đáp án của câu đó.

Câu 1: Biết $F(x)$ là một nguyên hàm của hàm số 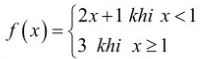. Giá trị $F(-1)$ bằng bao nhiều?

Câu 2: Biết $\int_0^e \frac{e^{-x} + 2}{e^{x-1}} dx = ae + b + \frac{c}{e}$ $(a, b, c \in \mathbb{R})$. Giá trị của $P = a + b + c$ bằng bao nhiều?

Câu 3: Chấp hành theo “Luật trật tự an toàn giao thông đường bộ”, Chị Nga đang lái xe với vận tốc $5m/s$ thì nhận thấy phía trước đèn giao thông đang chuyển sang đèn vàng và muốn giảm tốc độ của xe để dời đến đỏ. Sau khi đạp phanh, xe chuyển động chậm dần đều với vận tốc $v(t) = -0,7t + 5(m/s)$, trong đó $t$ là thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến khi xe dừng hẳn, xe đi chuyển quãng đường bao nhiều mét? (Kết quả làm tròn đến hàng phần mười).

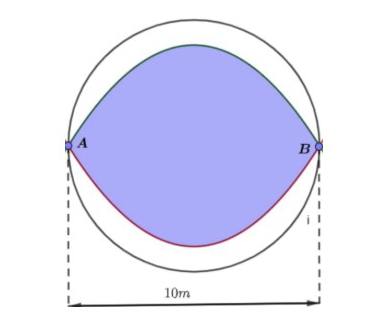
Câu 4: Trong khu vực trung tâm của một công viên lớn, có một miếng đất có dạng hình tròn đường kính $AB = 10(m)$. Người ta trang trí khu vực này bằng hai đường Parabol đối xứng nhau qua $AB$, nằm trong hình tròn, đi qua các điểm $A; B$ và có đỉnh cách mép hình tròn $1m$. Phần giới hạn bởi hai Parabol được trồng hoa với chi phí $300$ nghìn đồng $1m^2$, phần còn lại được lát gạch sứ với chi phí $700$ nghìn đồng $1m^2$. Tính tổng chi phí (triệu đồng) để hoàn thành khu vực này (kết quả làm tròn đến hàng phần mười)?

Câu 5: Từ mặt nước trong một bể nước, tại ba vị trí đối một cách nhau $2m$, người ta thả dây dội để qua dội chạm đáy bể. Phần dây dội (thẳng) nằm trong nước tại ba vị trí đó lần lượt có độ dài $4m; 4,4m; 4,8m$. Biết đáy bể là phẳng. Hỏi đáy bể nghiêng so với mặt phẳng nằm ngang một góc bao nhiều độ? Viết kết quả làm tròn đến hàng phần chục.

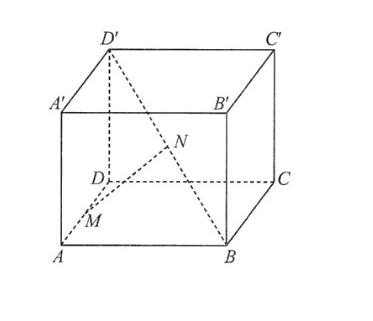
Câu 6: Có một chiếc lồng bằng sắt dạng hình hộp chữ nhật $ABCD.A’B’C’D’$ có $AB = 2m, AD = 3m, AA’ = 1m$. Người thợ hàn muốn hàn một thanh sắt $MN$ nối hai đoạn $AD$ và $BD$ (Hình). Tính chiều dài ngắn nhất của đoạn thanh sắt $MN$ (đơn vị mét) (làm tròn kết quả đến hàng phần trăm).

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh