PHẦN I. Câu trắc  nghiệm nhiều phương án lựa chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu thí sinh chỉ chọn một phương án.

Câu 1: Trong không gian $Oxyz$, mặt phẳng $(P)$ đi qua điểm $A(1;0;2)$ và nhận vectơ $\vec{n} = (1; -3; 5)$ làm vectơ pháp tuyến có phương trình tổng quát là
A. $x + 2z – 11 = 0$
B. $x + 2y – 5 = 0$
C. $x – 3y + 5z – 3 = 0$
D. $x – 3y + 5z – 11 = 0$

Câu 2: Trong không gian $Oxyz$, vectơ nào sau đây không phải là vectơ pháp tuyến của mặt phẳng $(P): x + 3y – 5z + 2 = 0$?
A. $\vec{n} = (-3; -9; 15)$
B. $\vec{n} = (-1; -3; 5)$
C. $\vec{n} = (2; 6; -10)$
D. $\vec{n} = (-2; -6; -10)$

Câu 3: Cho $f(x), g(x)$ là hàm số liên tục trên $K$, $k$ là hằng số khác 0. Mệnh đề nào sau đây là sai?
A. $\int [f(x) – g(x)] dx = \int f(x) dx – \int g(x) dx$
B. $\int [f(x) + g(x)] dx = \int f(x) dx + \int g(x) dx$
C. $\int [f(x) \cdot g(x)] dx = \int f(x) dx \cdot \int g(x) dx$
D. $\int k \cdot f(x) dx = k \cdot \int f(x) dx$

Câu 4: Trong không gian với hệ tọa độ $Oxyz$, cho $A(-3; 4; 2)$, $B(-5; 6; 2)$. Mặt phẳng $(P)$ đi qua $A$ và vuông góc với $AB$ có phương trình là
A. $x – y + 1 = 0$
B. $x – y – 1 = 0$
C. $-2x + 2y – 1 = 0$
D. $2x – 2y – 1 = 0$

Câu 5: Cho $f(x)$ liên tục trên đoạn $[a; b]$. Nếu $F(x)$ là một nguyên hàm của $f(x)$ trên đoạn $[a; b]$ thì $\int_a^b f(x) dx$ bằng
A. $F(b) – F(a)$
B. $F(a) + F(b)$
C. $F(a) – F(b)$
D. $F(b)$

Câu 6: Hàm số $f(x) = x^4 – 3x^2$ có họ nguyên hàm là
A. $F(x) = x^3 – 6x + C$
B. $F(x) = x^5 + x^3 + C$
C. $F(x) = \frac{x^5}{5} – x^3 + C$
D. $F(x) = \frac{x^5}{5} + x^3 + C$

Câu 7: Khoảng cách từ điểm $A(0;4;3)$ đến mặt phẳng $(P):3x-4z+1=0$ bằng
A. 7
B. 3
C. $\frac{16}{5}$
D. $\frac{11}{5}$

Câu 8: Cho $\int_0^2 f(x)dx = 3$ và $\int_0^2 g(x)dx = -1$. Tính $\int_0^2 [5g(x) + f(x)]dx$
A. 12
B. 0
C. 8
D. 10

Câu 9: Trong không gian với hệ tọa độ $Oxyz$, mặt phẳng $(P):x-2y+3z-1=0$ song song với mặt phẳng có phương trình nào sau đây?
A. $x-2y+3=0$
B. $x+2y+3z=0$
C. $x-2y+3z=0$
D. $x-2y-1=0$

Câu 10: Giả sử $F(x)$ là một nguyên hàm của $f(x)$ trên khoảng K và C là hằng số. Mệnh đề nào sau đây đúng?
A. $f'(x)=F(x)$
B. $F(x)=f(x)+C$
C. $F'(x)=f(x)$
D. $f(x)=F(x)+C$

Câu 11: Diện tích hình phẳng giới hạn bởi đường thẳng $y=2x+1$ và đồ thị hàm số $y=x^2-x+3$ là:
A. $\frac{1}{5}$
B. $\frac{1}{6}$
C. $\frac{1}{4}$
D. $\frac{1}{3}$

Câu 12: Trong không gian với hệ tọa độ $Oxyz$, mặt phẳng $(P):x-2y+3z-1=0$ vuông góc với mặt phẳng có phương trình nào sau đây?
A. $x+y-z+3=0$
B. $x-y-z+2=0$
C. $x-2y+3z+1=0$
D. $x-2y-3=0$

PHẦN II. Câu trắc nghiệm đúng sai

Câu 1: Cho hàm số $y = F(x)$ là một nguyên hàm của hàm số $f(x) = 2x – \cos x$ thoả mãn $F(0) = \ln 2$.

a) $\int f(x) dx = \int 2x dx – \int \cos x dx$

b) $F'(\pi) = 2\pi – 1$

c) Hệ số góc của tiếp tuyến với đồ thị hàm số $y = F(x)$ tại điểm có hoành độ $x_0 = \frac{\pi}{2}$ là $k = 2\pi$

d) Nếu $F(-1) = \frac{1 + \sin b}{a \ln a}$ với $a, b \in \mathbb{N}$ thì $a + 2b = 5$

Câu 2: Hình bên dưới minh họa mặt cắt đứng của một bức tường cũ có dạng hình chữ nhật với cổng ra vào có dạng hình parabol với các kích thước được cho như trong hình. Người ta dự định sơn lại mặt ngoài bức tường đó với chi phí là 125000 đồng/m².

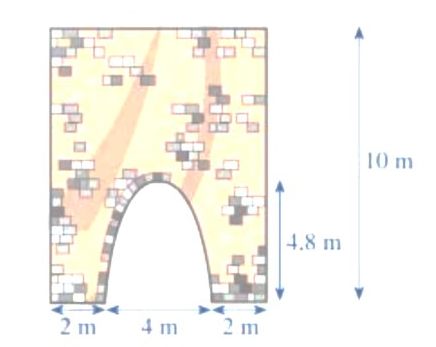
a) Cổng có chiều cao 4,8m.

b) Diện tích bức tường (bao gồm cả phần tường và phần cổng) là 40m².

c) Chọn hệ tọa độ $Oxy$ sao cho trục $Ox$ đi qua 2 chân cổng, trục $Oy$ đi qua đỉnh cổng. Khi đó hình dạng của cổng được mô tả bởi $(P): y = -1,2x^2 + 4,8$.

Câu 3: Trong không gian $Oxyz$, cho ba điểm $A(3;0;0)$, $B(1;2;1)$, $C(2;-1;2)$.

a) Mặt phẳng $(ABC)$ có một cặp vector chỉ phương là: $\overrightarrow{AB}$, $\overrightarrow{AC}$.

b) Mặt phẳng $(ABC)$ có một vector pháp tuyến là $\vec{n} = (5;3;4)$.

c) Biết mặt phẳng $(OBC)$ có một vector pháp tuyến là $(1;b;c)$. Khi đó $b + c = -1$.

d) Gọi $I$ là tâm mặt cầu nội tiếp tứ diện $O.ABC$, $(\alpha)$ là mặt phẳng đi qua 3 điểm $B, C, I$. Biết $(\alpha)$ có một vector pháp tuyến là $(a;b;3)$. Khi đó $a + b = 1$.

Câu 4: Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và thỏa mãn $\int_{1}^{4} f(x) dx = \frac{1186}{45}$. Các mệnh đề sau đây đúng hay sai?

a) Khi $\int_{1}^{9} f(x) dx = \frac{2268}{5}$ thì biểu thức $I = \int_{x}^{9} f(x) dx = \frac{19226}{45}$.

b) $\int_{1}^{4} \left[ \frac{45}{2} f(x) + 2 \right] dx = 559$.

c) Biết hàm số $f(x)$ đồng biến, có đạo hàm trên đoạn $[1;4]$ và thỏa mãn $x + 2x \cdot f(x) = [f'(x)]^2$ với $\forall x \in [1;4]$ thì $\sqrt{x} dx = \sqrt{1 + 2f(x)}$.

d) Cho $f(1) = \frac{3}{2}$ thì hàm số $f(x) = \frac{2}{9} x^3 + \frac{8}{9} x^{\frac{3}{2}} + \frac{4}{3}$.

PHẦN III. Câu trắc nghiệm trả lời ngắn

Câu 1: Hàm cầu liên quan đến giá $P$ của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá $P$ của sản phẩm với mức độ sẵn sàng cung cấp sản phẩm của nhà sản xuất. Điểm cắt nhau $(x_0; p_0)$ của đồ thị hàm cầu $p = D(x)$ và đồ thị hàm cung $p = S(x)$ được gọi là điểm cân bằng. Thặng dư tiêu dùng là diện tích hình phẳng giới hạn bởi đồ thị hàm cầu, đường ngang $p = p_0$ và đường thẳng đứng $x = 0$. Thặng dư sản xuất là diện tích hình phẳng giới hạn bởi đồ thị hàm cung, đường ngang $p = p_0$ và đường thẳng đứng $x = 0$.

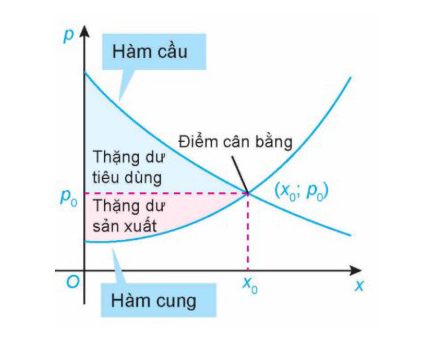
Biết: Đơn đặt hàng của nhà máy cho một loại máy lọc không khí là khoảng 6000 chiếc mỗi tuần khi giá là 375 USD/chiếc và khoảng 8000 chiếc mỗi tuần khi giá là 305 USD/chiếc. Hàm cung được cho bởi $p = S(x) = \frac{1}{55}x$, trong đó $x$ là số lượng máy lọc không khí được bán với giá $P$ USD một chiếc. Tìm thặng dư tiêu dùng (giả sử hàm cầu là hàm số bậc nhất và kết quả làm tròn đến hàng nghìn).

Câu 2: Trong không gian với hệ trục tọa độ $Oxyz$, cho hai mặt phẳng $(P_1): 4x – 3m^2y – 2z + 4 = 0$ và $(P_2): 5x – 2y + 13z + m + 9 = 0$ với $m$ là tham số. Tìm số giá trị nguyên dương của tham số $m$ để $(P_1) \perp (P_2)$.

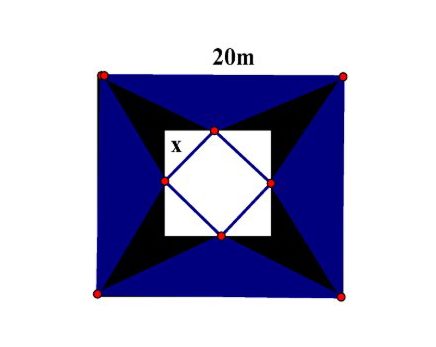
Câu 3: Để làm mô hình kim tự tháp dạng hình chóp tứ giác đều người ta cắt một tấm nhôm hình vuông cạnh bằng $20m$ để dán thành một hình chóp tứ giác đều sao cho bốn đỉnh của hình vuông dán lại thành đỉnh của hình chóp như hình vẽ. Để tận dụng không gian họ định dùng phần ruột của khối chóp đó chứa nước (Coi các phần cắt và dán là không đáng kể). Khi chứa được lượng nước nhiều nhất thì khoảng cách từ đỉnh chóp đến mặt đáy chóp bằng (kết quả làm tròn đến hàng phần trăm).

Câu 4: Cho $f'(x) = 2x – 12$ và $f(1) = 29$. Phương trình $f(x) = 8$ có hai nghiệm $x_1, x_2$. Tổng $S = \log_2 |x_1| + \log_2 |x_2|$ bằng.

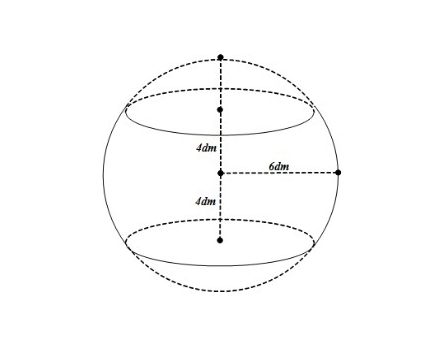
Câu 5: Một hình cầu có bán kính 6dm, người ta cắt bỏ hai phần bằng hai mặt phẳng song song và cùng vuông góc với đường kính để làm mặt xung quanh của một chiếc lu chứa nước (như hình vẽ). Tính thể tích $V(dm^3)$ mà chiếc lu chứa được biết mặt phẳng cách tâm mặt cầu 4dm. (Kết quả làm tròn đến hàng đơn vị).

Câu 6: Cho hàm số $f(x)$ liên tục và có đạo hàm tại mọi $x \in (0; +\infty)$ đồng thời thỏa mãn điều kiện:
$f(x) = x(\sin x + f'(x)) + \cos x$ và $\int_{\frac{\pi}{2}}^{\frac{3\pi}{2}} f(x) \sin x dx = -4$.
Biết $f(\pi) = a\pi + b$. Tính kết quả của $ab$.

Đáp Án

ThS. Lê Thị Thuý Nga

(Người kiểm duyệt, ra đề)

Chức vụ: Trưởng ban biên soạn môn Toán THPT

Trình độ: Thạc sĩ Lý luận dạy học Toán, Chứng chỉ hạng II, Chứng chỉ Tin học, Ngoại ngữ B1

Kinh nghiệm: 11+ năm kinh nghiệm tại Trường THPT Lương Thế Vinh