Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ HÌNH NÓN CỤT
- 1. Hình nón cụt là gì?
- 2. Các thành phần của hình nón cụt
- 3. Phân biệt hình nón và hình nón cụt
- II. CÔNG THỨC DIỆN TÍCH ĐÁY
- 1. Diện tích đáy lớn
- 2. Diện tích đáy nhỏ
- 3. Tổng diện tích hai đáy
- III. CÔNG THỨC DIỆN TÍCH XUNG QUANH
- 1. Công thức diện tích xung quanh
- 2. Công thức tính đường sinh
- 3. Ví dụ minh họa
- IV. CÔNG THỨC DIỆN TÍCH TOÀN PHẦN
- 1. Công thức
- 2. Ví dụ minh họa
- V. CÔNG THỨC THỂ TÍCH HÌNH NÓN CỤT
- 1. Công thức thể tích
- 2. Cách suy ra công thức
- 3. Công thức đặc biệt
- 4. Ví dụ minh họa
- VII. BÀI TẬP MẪU CÓ LỜI GIẢI
- VIII. MẸO VÀ LƯU Ý
- 1. Các sai lầm thường gặp
- 2. Mẹo nhớ công thức thể tích
- 3. Quy tắc vàng giải bài
- 4. Quan hệ đặc biệt
- IX. KẾT LUẬN
- 3 điểm cốt lõi cần nhớ
- Tài liệu tham khảo
I. GIỚI THIỆU VỀ HÌNH NÓN CỤT
1. Hình nón cụt là gì?
Định nghĩa: Hình nón cụt là phần hình nón còn lại sau khi cắt bỏ đỉnh bởi một mặt phẳng song song với đáy.
Hình dung trực quan:
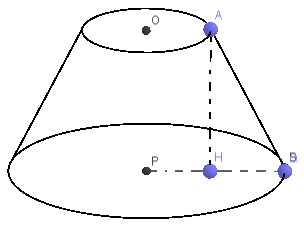
Cách hình thành hình nón cụt:
Bước 1: Xuất phát từ một hình nón đầy đủ có:
- Bán kính đáy: $R$ (đáy lớn)
- Chiều cao: $H$ (chiều cao tổng)
- Đỉnh ở trên cùng
Bước 2: Dùng mặt phẳng song song với đáy cắt ngang hình nón tại một vị trí nào đó:
- Mặt phẳng cắt tạo ra một đường tròn mới có bán kính $r$ (đáy nhỏ)
- Mặt phẳng này phải song song hoàn toàn với đáy ban đầu
Bước 3: Bỏ đi phần đỉnh (nón nhỏ phía trên):
- Phần còn lại chính là hình nón cụt
- Có hai đáy: đáy lớn (R) và đáy nhỏ (r)
- Chiều cao hình nón cụt: $h$ (khoảng cách giữa hai đáy)
2. Các thành phần của hình nón cụt
| Thành phần | Ký hiệu | Mô tả chi tiết |
|---|---|---|
| Đáy lớn | $R$ | Bán kính của đáy lớn (đáy dưới), luôn lớn hơn $r$ |
| Đáy nhỏ | $r$ | Bán kính của đáy nhỏ (đáy trên), luôn nhỏ hơn $R$ |
| Chiều cao | $h$ | Khoảng cách vuông góc giữa hai mặt đáy |
| Đường sinh | $l$ | Độ dài đoạn thẳng nối một điểm trên đường tròn đáy lớn với điểm tương ứng trên đường tròn đáy nhỏ |
Quan hệ Pythagore quan trọng:
Trong hình nón cụt, ba đại lượng $l$, $h$, $(R-r)$ tạo thành một tam giác vuông, do đó:
$$\boxed{l^2 = h^2 + (R – r)^2}$$
Từ đó suy ra:
- $l = \sqrt{h^2 + (R-r)^2}$ (khi biết $h$, $R$, $r$)
- $h = \sqrt{l^2 – (R-r)^2}$ (khi biết $l$, $R$, $r$)
Lưu ý quan trọng: Luôn sử dụng hiệu $(R – r)$, không phải tổng $(R + r)$ trong công thức Pythagore!
3. Phân biệt hình nón và hình nón cụt
| Đặc điểm | Hình nón | Hình nón cụt |
|---|---|---|
| Số đáy | 1 đáy duy nhất | 2 đáy (lớn và nhỏ) |
| Đỉnh | Có đỉnh nhọn | Không có đỉnh (đã cắt bỏ) |
| Cạnh bên | Hội tụ về một điểm | Song song, không hội tụ |
| Công thức | Đơn giản hơn | Phức tạp hơn, có thêm $r$ |
| Hình dạng | Nhọn ở đỉnh | Cụt, phẳng ở trên |
Mối quan hệ: Hình nón là trường hợp đặc biệt của hình nón cụt khi $r = 0$ (đáy nhỏ co lại thành điểm).
II. CÔNG THỨC DIỆN TÍCH ĐÁY
1. Diện tích đáy lớn
Đáy lớn là một hình tròn có bán kính $R$:
$$\boxed{S_{\text{đáy lớn}} = \pi R^2}$$
Trong đó:
- $\pi \approx 3.14$ hoặc $\frac{22}{7}$
- $R$ là bán kính đáy lớn (đơn vị: cm, m, dm)
2. Diện tích đáy nhỏ
Đáy nhỏ là một hình tròn có bán kính $r$:
$$\boxed{S_{\text{đáy nhỏ}} = \pi r^2}$$
Trong đó:
- $r$ là bán kính đáy nhỏ (đơn vị: cm, m, dm)
3. Tổng diện tích hai đáy
Khi cần tính diện tích toàn phần, ta cần tổng diện tích của cả hai đáy:
$$\boxed{S_{\text{2 đáy}} = \pi R^2 + \pi r^2 = \pi(R^2 + r^2)}$$
Ví dụ: Hình nón cụt có $R = 5$ cm, $r = 3$ cm. Tính tổng diện tích hai đáy.
Lời giải:
Cách 1: Tính từng đáy rồi cộng lại
- Diện tích đáy lớn: $S_1 = 3.14 \times 5^2 = 3.14 \times 25 = 78.5$ cm²
- Diện tích đáy nhỏ: $S_2 = 3.14 \times 3^2 = 3.14 \times 9 = 28.26$ cm²
- Tổng: $S = 78.5 + 28.26 = 106.76$ cm²
Cách 2: Dùng công thức rút gọn $$S_{\text{2 đáy}} = \pi(R^2 + r^2) = 3.14(25 + 9) = 3.14 \times 34 = 106.76 \text{ cm}^2$$
Kết luận: Tổng diện tích hai đáy là 106.76 cm².
III. CÔNG THỨC DIỆN TÍCH XUNG QUANH
1. Công thức diện tích xung quanh
Diện tích xung quanh của hình nón cụt là diện tích mặt cong bao quanh (không tính hai đáy):
$$\boxed{S_{xq} = \pi(R + r)l}$$
Trong đó:
- $R$: Bán kính đáy lớn
- $r$: Bán kính đáy nhỏ
- $l$: Đường sinh (độ dài cạnh bên)
Cách nhớ: “Pi nhân tổng hai bán kính nhân đường sinh”
Giải thích công thức:
Khi “trải phẳng” mặt xung quanh của hình nón cụt ra, ta được một hình quạt tròn (hay hình vành khuyên). Diện tích của hình này được tính theo công thức trên.
Lưu ý quan trọng:
- Dùng tổng $(R + r)$ trong công thức diện tích xung quanh
- Khác với công thức Pythagore dùng hiệu $(R – r)$
2. Công thức tính đường sinh
Nếu đề bài không cho sẵn đường sinh $l$, ta phải tính từ các đại lượng khác:
$$\boxed{l = \sqrt{h^2 + (R – r)^2}}$$
Giải thích: Đây là hệ quả trực tiếp của định lý Pythagore trong tam giác vuông được tạo bởi:
- Cạnh huyền: đường sinh $l$
- Cạnh góc vuông thứ nhất: chiều cao $h$
- Cạnh góc vuông thứ hai: hiệu bán kính $(R – r)$
Chú ý: Phải dùng trừ $(R – r)$, không phải cộng!
3. Ví dụ minh họa
Ví dụ 1: Hình nón cụt có $R = 6$ cm, $r = 4$ cm, $l = 5$ cm. Tính diện tích xung quanh.
Lời giải:
Áp dụng công thức: $$S_{xq} = \pi(R + r)l$$ $$= 3.14 \times (6 + 4) \times 5$$ $$= 3.14 \times 10 \times 5$$ $$= 157 \text{ cm}^2$$
Kết luận: Diện tích xung quanh là 157 cm².
Ví dụ 2: Hình nón cụt có $R = 8$ cm, $r = 5$ cm, $h = 4$ cm. Tính diện tích xung quanh.
Lời giải:
Đề bài không cho $l$, nên ta phải tính đường sinh trước.
Bước 1: Tính đường sinh $$l = \sqrt{h^2 + (R-r)^2}$$ $$= \sqrt{4^2 + (8-5)^2}$$ $$= \sqrt{16 + 9}$$ $$= \sqrt{25} = 5 \text{ cm}$$
Bước 2: Tính diện tích xung quanh $$S_{xq} = \pi(R + r)l$$ $$= 3.14 \times (8 + 5) \times 5$$ $$= 3.14 \times 13 \times 5$$ $$= 204.1 \text{ cm}^2$$
Kết luận: Diện tích xung quanh là 204.1 cm².
IV. CÔNG THỨC DIỆN TÍCH TOÀN PHẦN
1. Công thức
Diện tích toàn phần là tổng diện tích xung quanh và diện tích hai đáy:
$$\boxed{S_{tp} = S_{xq} + S_{\text{2 đáy}}}$$
Khai triển: $$S_{tp} = \pi(R + r)l + \pi(R^2 + r^2)$$
Rút gọn: $$\boxed{S_{tp} = \pi[(R + r)l + R^2 + r^2]}$$
Trong đó:
- $S_{xq} = \pi(R + r)l$: Diện tích xung quanh
- $S_{\text{2 đáy}} = \pi(R^2 + r^2)$: Tổng diện tích hai đáy
Công thức này dùng khi: Cần tính lượng vật liệu để làm một vật hình nón cụt kín (có cả hai đáy).
2. Ví dụ minh họa
Ví dụ: Hình nón cụt có $R = 5$ cm, $r = 3$ cm, $l = 4$ cm. Tính diện tích toàn phần.
Lời giải:
Cách 1: Tính từng phần rồi cộng
Bước 1: Tính diện tích xung quanh $$S_{xq} = \pi(R + r)l = 3.14 \times (5+3) \times 4 = 3.14 \times 8 \times 4 = 100.48 \text{ cm}^2$$
Bước 2: Tính tổng diện tích hai đáy $$S_{\text{2 đáy}} = \pi(R^2 + r^2) = 3.14 \times (25 + 9) = 3.14 \times 34 = 106.76 \text{ cm}^2$$
Bước 3: Tính diện tích toàn phần $$S_{tp} = 100.48 + 106.76 = 207.24 \text{ cm}^2$$
Cách 2: Dùng công thức rút gọn
$$S_{tp} = \pi[(R + r)l + R^2 + r^2]$$ $$= 3.14 \times [(8 \times 4) + 25 + 9]$$ $$= 3.14 \times [32 + 25 + 9]$$ $$= 3.14 \times 66$$ $$= 207.24 \text{ cm}^2$$
Kết luận: Diện tích toàn phần là 207.24 cm².
Ứng dụng: Biết diện tích toàn phần giúp tính lượng vật liệu (giấy, tôn, nhựa…) cần dùng để làm vật thể hình nón cụt.
V. CÔNG THỨC THỂ TÍCH HÌNH NÓN CỤT
1. Công thức thể tích
Đây là công thức quan trọng nhất của hình nón cụt:
$$\boxed{V = \frac{1}{3}\pi h(R^2 + Rr + r^2)}$$
Trong đó:
- $h$: Chiều cao (khoảng cách giữa hai đáy)
- $R$: Bán kính đáy lớn
- $r$: Bán kính đáy nhỏ
- $\pi \approx 3.14$ hoặc $\frac{22}{7}$
Cách nhớ: “Một phần ba pi h nhân ngoặc R bình cộng R nhân r cộng r bình”
Đặc điểm quan trọng của công thức:
- Có hệ số $\frac{1}{3}$ (giống hình nón)
- Có ba số hạng trong ngoặc: $R^2$, $Rr$, $r^2$
- Thứ tự: từ lớn đến nhỏ, từ $R$ đến $r$
2. Cách suy ra công thức
Phương pháp: Thể tích nón cụt = Thể tích nón lớn – Thể tích nón nhỏ (bị cắt bỏ)
Giả sử:
- Nón lớn ban đầu có chiều cao $H$, bán kính đáy $R$
- Cắt bỏ phần đỉnh (nón nhỏ) có chiều cao $(H – h)$, bán kính đáy $r$
- Phần còn lại là nón cụt có chiều cao $h$
Tính toán:
Thể tích nón lớn: $$V_{\text{lớn}} = \frac{1}{3}\pi R^2 H$$
Thể tích nón nhỏ bị cắt: $$V_{\text{nhỏ}} = \frac{1}{3}\pi r^2(H – h)$$
Thể tích nón cụt: $$V = V_{\text{lớn}} – V_{\text{nhỏ}} = \frac{1}{3}\pi R^2 H – \frac{1}{3}\pi r^2(H – h)$$
Sau khi biến đổi và rút gọn (sử dụng tính chất tam giác đồng dạng): $$V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$$
3. Công thức đặc biệt
Trường hợp 1: Khi $r = 0$ (đáy nhỏ co lại thành điểm)
Hình nón cụt trở thành hình nón thông thường: $$V = \frac{1}{3}\pi h(R^2 + R \cdot 0 + 0^2) = \frac{1}{3}\pi h R^2$$
Đây chính là công thức thể tích hình nón! ✓
Trường hợp 2: Khi $R = r$ (hai đáy bằng nhau)
Hình nón cụt trở thành hình trụ: $$V = \frac{1}{3}\pi h(R^2 + R \cdot R + R^2) = \frac{1}{3}\pi h \cdot 3R^2 = \pi R^2 h$$
Đây chính là công thức thể tích hình trụ! ✓
4. Ví dụ minh họa
Ví dụ 1: Hình nón cụt có $R = 6$ cm, $r = 4$ cm, $h = 5$ cm. Tính thể tích.
Lời giải:
Áp dụng công thức: $$V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$$
Bước 1: Tính các số hạng trong ngoặc
- $R^2 = 6^2 = 36$
- $Rr = 6 \times 4 = 24$
- $r^2 = 4^2 = 16$
- Tổng: $36 + 24 + 16 = 76$
Bước 2: Tính thể tích $$V = \frac{1}{3} \times 3.14 \times 5 \times 76$$ $$= \frac{1}{3} \times 1193.2$$ $$= 397.73 \text{ cm}^3$$
Kết luận: Thể tích hình nón cụt là 397.73 cm³.
Ví dụ 2: Một cốc nước hình nón cụt có đường kính miệng 8 cm, đường kính đáy 6 cm, chiều cao 10 cm. Tính dung tích cốc (đơn vị: ml).
Lời giải:
Chuyển đổi: Đường kính → bán kính
- Bán kính miệng: $R = \frac{8}{2} = 4$ cm
- Bán kính đáy: $r = \frac{6}{2} = 3$ cm
- Chiều cao: $h = 10$ cm
Tính toán: $$V = \frac{1}{3} \times 3.14 \times 10 \times (16 + 12 + 9)$$ $$= \frac{1}{3} \times 3.14 \times 10 \times 37$$ $$= \frac{1161.8}{3} = 387.93 \text{ cm}^3$$
Chuyển đổi đơn vị: $1$ cm³ $= 1$ ml
Kết luận: Dung tích cốc là 387.93 ml $\approx 388$ ml.
Ví dụ 3: Hình nón cụt có $R = 10$ cm, $r = 5$ cm, đường sinh $l = 13$ cm. Tính thể tích.
Lời giải:
Đề bài cho đường sinh $l$ nhưng công thức thể tích cần chiều cao $h$. Ta phải tính $h$ trước.
Bước 1: Tính chiều cao từ công thức Pythagore $$l^2 = h^2 + (R – r)^2$$ $$13^2 = h^2 + (10 – 5)^2$$ $$169 = h^2 + 25$$ $$h^2 = 144$$ $$h = 12 \text{ cm}$$
Bước 2: Tính thể tích $$V = \frac{1}{3} \times 3.14 \times 12 \times (100 + 50 + 25)$$ $$= \frac{1}{3} \times 3.14 \times 12 \times 175$$ $$= \frac{6594}{3} = 2198 \text{ cm}^3$$
Kết luận: Thể tích là 2198 cm³.
VII. BÀI TẬP MẪU CÓ LỜI GIẢI
Dạng 1: Tính diện tích và thể tích cơ bản
Bài 1: Hình nón cụt có $R = 8$ cm, $r = 5$ cm, $h = 4$ cm. Tính: a) Đường sinh
b) Diện tích xung quanh
c) Thể tích
Lời giải:
Câu a) Tính đường sinh:
Áp dụng công thức Pythagore: $$l = \sqrt{h^2 + (R-r)^2}$$ $$= \sqrt{4^2 + (8-5)^2}$$ $$= \sqrt{16 + 9}$$ $$= \sqrt{25} = 5 \text{ cm}$$
Câu b) Tính diện tích xung quanh:
$$S_{xq} = \pi(R+r)l$$ $$= 3.14 \times (8+5) \times 5$$ $$= 3.14 \times 13 \times 5$$ $$= 204.1 \text{ cm}^2$$
Câu c) Tính thể tích:
$$V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$$ $$= \frac{1}{3} \times 3.14 \times 4 \times (64 + 40 + 25)$$ $$= \frac{1}{3} \times 3.14 \times 4 \times 129$$ $$= \frac{1620.48}{3} = 540.16 \text{ cm}^3$$
Kết luận:
- Đường sinh: 5 cm
- Diện tích xung quanh: 204.1 cm²
- Thể tích: 540.16 cm³
Dạng 2: Bài toán thực tế – Cốc nước
Bài 2: Một cốc giấy hình nón cụt có đường kính miệng 9 cm, đường kính đáy 6 cm, chiều cao 12 cm. a) Tính dung tích cốc (ml)
b) Tính diện tích giấy cần dùng để làm cốc (kể cả đáy)
Lời giải:
Chuyển đổi dữ liệu:
- Bán kính miệng: $R = \frac{9}{2} = 4.5$ cm
- Bán kính đáy: $r = \frac{6}{2} = 3$ cm
- Chiều cao: $h = 12$ cm
Câu a) Tính dung tích:
$$V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$$ $$= \frac{1}{3} \times 3.14 \times 12 \times (20.25 + 13.5 + 9)$$ $$= \frac{1}{3} \times 3.14 \times 12 \times 42.75$$ $$= \frac{1607.58}{3} = 535.86 \text{ cm}^3$$
Chuyển đổi: $535.86$ cm³ $≈ 536$ ml
Câu b) Tính diện tích giấy:
Bước 1: Tính đường sinh $$l = \sqrt{h^2 + (R-r)^2}$$ $$= \sqrt{144 + (1.5)^2}$$ $$= \sqrt{144 + 2.25}$$ $$= \sqrt{146.25} \approx 12.09 \text{ cm}$$
Bước 2: Tính diện tích toàn phần $$S_{tp} = \pi[(R+r)l + R^2 + r^2]$$ $$= 3.14 \times [(7.5 \times 12.09) + 20.25 + 9]$$ $$= 3.14 \times [90.675 + 29.25]$$ $$= 3.14 \times 119.925$$ $$\approx 376.57 \text{ cm}^2$$
Kết luận:
- Dung tích cốc: 536 ml
- Diện tích giấy cần dùng: 376.57 cm²
Dạng 3: Tính ngược chiều cao
Bài 3: Hình nón cụt có $R = 10$ cm, $r = 6$ cm, thể tích $V = 1005.28$ cm³. Tính chiều cao.
Lời giải:
Từ công thức thể tích: $$V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$$
Suy ra: $$h = \frac{3V}{\pi(R^2 + Rr + r^2)}$$
Tính toán:
Bước 1: Tính mẫu số $$R^2 + Rr + r^2 = 100 + 60 + 36 = 196$$
Bước 2: Tính chiều cao $$h = \frac{3 \times 1005.28}{3.14 \times 196}$$ $$= \frac{3015.84}{615.44}$$ $$\approx 4.9 \text{ cm}$$
Kết luận: Chiều cao là 4.9 cm ≈ 5 cm.
Dạng 4: So sánh với hình nón
Bài 4: Cắt hình nón có bán kính đáy $R = 10$ cm, chiều cao 12 cm bởi mặt phẳng song song với đáy, cách đỉnh 3 cm. Tính thể tích phần nón cụt còn lại.
Lời giải:
Phân tích:
- Nón ban đầu: $R = 10$ cm, $H = 12$ cm
- Cắt cách đỉnh 3 cm → chiều cao nón cụt: $h = 12 – 3 = 9$ cm
- Phần bị cắt (nón nhỏ): chiều cao $h_1 = 3$ cm
Bước 1: Tìm bán kính đáy nhỏ $r$
Do tam giác đồng dạng: $$\frac{r}{h_1} = \frac{R}{H}$$ $$\frac{r}{3} = \frac{10}{12}$$ $$r = \frac{10 \times 3}{12} = 2.5 \text{ cm}$$
Bước 2: Tính thể tích nón nhỏ bị cắt $$V_{\text{nhỏ}} = \frac{1}{3}\pi r^2 h_1$$ $$= \frac{1}{3} \times 3.14 \times 6.25 \times 3$$ $$= \frac{58.875}{3} = 19.625 \text{ cm}^3$$
Bước 3: Tính thể tích nón lớn ban đầu $$V_{\text{lớn}} = \frac{1}{3}\pi R^2 H$$ $$= \frac{1}{3} \times 3.14 \times 100 \times 12$$ $$= \frac{3768}{3} = 1256 \text{ cm}^3$$
Bước 4: Tính thể tích nón cụt $$V_{\text{cụt}} = V_{\text{lớn}} – V_{\text{nhỏ}}$$ $$= 1256 – 19.625$$ $$= 1236.375 \text{ cm}^3$$
Kiểm tra bằng công thức trực tiếp: $$V_{\text{cụt}} = \frac{1}{3} \times 3.14 \times 9 \times (100 + 25 + 6.25)$$ $$= \frac{1}{3} \times 3.14 \times 9 \times 131.25 = 1236.375 \text{ cm}^3$$ ✓
Kết luận: Thể tích nón cụt còn lại là 1236.375 cm³.
Dạng 5: Bài toán tối ưu
Bài 5: Một xô nước hình nón cụt bằng sắt có $R = 20$ cm, $r = 15$ cm, $h = 30$ cm. Tính: a) Dung tích xô (lít)
b) Diện tích sắt cần dùng (không kể nắp)
Lời giải:
Câu a) Tính dung tích:
$$V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$$ $$= \frac{1}{3} \times 3.14 \times 30 \times (400 + 300 + 225)$$ $$= \frac{1}{3} \times 3.14 \times 30 \times 925$$ $$= 31.4 \times 925$$ $$= 29045 \text{ cm}^3$$
Chuyển đổi: $29045$ cm³ $= 29.045$ lít
Câu b) Tính diện tích sắt:
Không kể nắp nghĩa là tính: Diện tích xung quanh + Diện tích đáy lớn
Bước 1: Tính đường sinh $$l = \sqrt{h^2 + (R-r)^2}$$ $$= \sqrt{900 + 25}$$ $$= \sqrt{925} \approx 30.41 \text{ cm}$$
Bước 2: Tính diện tích xung quanh $$S_{xq} = \pi(R + r)l$$ $$= 3.14 \times 35 \times 30.41$$ $$\approx 3343.89 \text{ cm}^2$$
Bước 3: Tính diện tích đáy lớn $$S_{\text{đáy}} = \pi R^2 = 3.14 \times 400 = 1256 \text{ cm}^2$$
Bước 4: Tổng diện tích $$S = S_{xq} + S_{\text{đáy}} = 3343.89 + 1256 = 4599.89 \text{ cm}^2$$
Chuyển đổi: $4599.89$ cm² $≈ 0.46$ m²
Kết luận:
- Dung tích xô: 29.045 lít
- Diện tích sắt: 4599.89 cm² ≈ 0.46 m²
VIII. MẸO VÀ LƯU Ý
1. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm $(R – r)$ thành $(R + r)$ trong công thức Pythagore
Sai:
- $l = \sqrt{h^2 + (R + r)^2}$ ❌
Đúng:
- $l = \sqrt{h^2 + (R – r)^2}$ ✓
Giải thích: Trong tam giác vuông, cạnh góc vuông là hiệu hai bán kính, không phải tổng!
❌ SAI LẦM 2: Quên hệ số $\frac{1}{3}$ trong công thức thể tích
Sai:
- $V = \pi h(R^2 + Rr + r^2)$ ❌
Đúng:
- $V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$ ✓
Cách nhớ: Mọi khối có đỉnh (nón, chóp) đều có hệ số $\frac{1}{3}$ trong công thức thể tích!
❌ SAI LẦM 3: Dùng $(R – r)$ thay vì $(R + r)$ khi tính diện tích xung quanh
Sai:
- $S_{xq} = \pi(R – r)l$ ❌
Đúng:
- $S_{xq} = \pi(R + r)l$ ✓
Quy tắc:
- Đường sinh $l$ dùng hiệu $(R – r)$
- Diện tích xung quanh dùng tổng $(R + r)$
❌ SAI LẦM 4: Nhầm công thức thể tích thiếu số hạng $Rr$
Sai:
- $V = \frac{1}{3}\pi h(R^2 + r^2)$ ❌
Đúng:
- $V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$ ✓
Cách nhớ: Ba số hạng theo thứ tự: $R^2$ (lớn nhất), $Rr$ (ở giữa), $r^2$ (nhỏ nhất)
2. Mẹo nhớ công thức thể tích
Công thức: $V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$
Cách nhớ 1: “R bình, R nhân r, r bình” – ba số hạng theo thứ tự giảm dần từ R về r
Cách nhớ 2: “Một phần ba pi h nhân ngoặc R bình cộng tích cộng r bình”
Kiểm tra tính đúng đắn:
Kiểm tra 1: Khi $r = 0$ (nón thường) $$V = \frac{1}{3}\pi h(R^2 + 0 + 0) = \frac{1}{3}\pi h R^2$$ ✓
Kiểm tra 2: Khi $R = r$ (hình trụ) $$V = \frac{1}{3}\pi h(R^2 + R^2 + R^2) = \frac{1}{3}\pi h \times 3R^2 = \pi R^2 h$$ ✓
Cả hai trường hợp đều cho kết quả đúng!
3. Quy tắc vàng giải bài
Bước 1: Xác định dữ liệu
- Gạch chân hoặc đánh dấu: $R$, $r$, $h$, $l$
- Lưu ý: $R$ luôn lớn hơn $r$ ($R > r$)
- Đổi đơn vị nếu cần (đường kính → bán kính, m → cm)
Bước 2: Kiểm tra đầy đủ dữ liệu
Nếu tính diện tích: Cần $R$, $r$, $l$
- Thiếu $l$? → Tính $l = \sqrt{h^2 + (R-r)^2}$
Nếu tính thể tích: Cần $R$, $r$, $h$
- Thiếu $h$? → Tính $h = \sqrt{l^2 – (R-r)^2}$
Bước 3: Áp dụng công thức
- Diện tích → dùng $l$, công thức có $(R + r)$
- Thể tích → dùng $h$, công thức có ba số hạng $R^2 + Rr + r^2$
Bước 4: Tính toán cẩn thận
- Tính từng bước nhỏ
- Kiểm tra đơn vị
- Làm tròn hợp lý (thường 2 chữ số thập phân)
Bước 5: Kiểm tra kết quả
- $V_{\text{nón cụt}}$ phải nhỏ hơn $V_{\text{trụ}}$ cùng $R$, $h$
- Diện tích không thể âm
- So sánh với ước lượng ban đầu
4. Quan hệ đặc biệt
Quan hệ 1: Khi $R = 2r$
Nếu bán kính đáy lớn gấp đôi đáy nhỏ và biết chiều cao $h$:
$$V = \frac{1}{3}\pi h(4r^2 + 2r^2 + r^2) = \frac{7\pi r^2 h}{3}$$
Ví dụ: $r = 3$ cm, $R = 6$ cm, $h = 5$ cm $$V = \frac{7 \times 3.14 \times 9 \times 5}{3} = 329.7 \text{ cm}^3$$
Quan hệ 2: So sánh với hình trụ
Với cùng $R$, $r$, $h$: $$V_{\text{nón cụt}} < V_{\text{trụ (R)}} = \pi R^2 h$$ $$V_{\text{nón cụt}} > V_{\text{trụ (r)}} = \pi r^2 h$$
Quan hệ 3: Tỉ lệ thể tích
Nếu cắt nón ở vị trí chiều cao bằng $\frac{1}{k}$ chiều cao tổng: $$\frac{V_{\text{phần cắt}}}{V_{\text{tổng}}} = \frac{1}{k^3}$$
IX. KẾT LUẬN
Bài viết đã tổng hợp đầy đủ các công thức hình nón cụt, bao gồm:
Công thức Pythagore: $$l^2 = h^2 + (R – r)^2$$
Công thức diện tích:
- Diện tích hai đáy: $\pi(R^2 + r^2)$
- Diện tích xung quanh: $S_{xq} = \pi(R + r)l$
- Diện tích toàn phần: $S_{tp} = \pi[(R+r)l + R^2 + r^2]$
Công thức thể tích: $$V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$$
3 điểm cốt lõi cần nhớ
1. Đường sinh dùng $(R – r)$ (hiệu – TRỪ!) $$l = \sqrt{h^2 + (R-r)^2}$$
2. Diện tích xung quanh dùng $(R + r)$ (tổng – CỘNG!) $$S_{xq} = \pi(R + r)l$$
3. Thể tích có ba số hạng: $R^2 + Rr + r^2$ $$V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$$
Tài liệu tham khảo
Xem thêm các chủ đề liên quan:
- [Công thức hình nón – Đầy đủ và chi tiết]
- [Công thức hình trụ – Bảng tổng hợp]
- [So sánh các khối tròn xoay: Nón, Nón cụt, Trụ]
- [Bài tập hình học không gian – Có lời giải]

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
