Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU
- 1. Góc giữa hai đường thẳng là gì?
- 2. Phân biệt với góc giữa hai vectơ
- 3. Các trường hợp đặc biệt
- 4. Cấu trúc bài viết
- II. CÔNG THỨC TRONG MẶT PHẲNG (2D)
- CÁCH 1: Dùng hệ số góc (Đường thẳng dạng $y = ax + b$)
- CÁCH 2: Dùng vectơ chỉ phương
- CÁCH 3: Dùng vectơ pháp tuyến (VTPT)
- So sánh 3 cách
- III. CÔNG THỨC TRONG KHÔNG GIAN (3D)
- CÔNG THỨC TỔNG QUÁT
- Các dạng phương trình đường thẳng trong không gian
- Ví dụ minh họa
- Lưu ý đặc biệt về trị tuyệt đối
- IV. CÁC TRƯỜNG HỢP ĐẶC BIỆT
- 1. Hai đường thẳng song song
- 2. Hai đường thẳng vuông góc
- 3. Góc giữa đường thẳng và trục tọa độ
- V. BÀI TẬP THỰC TẾ
- Bài tập 1: Góc nghiêng mái nhà
- Bài tập 2: Góc giao đường
- Bài tập 3: Góc hàn trong kỹ thuật
- Bài tập 4: Ranh giới thửa đất
- Bài tập 5: Góc bay máy bay
- VI. BẢNG TỔNG HỢP & MẸO NHỚ
- Bảng công thức tổng hợp
- Bảng trường hợp đặc biệt
- Quy trình 5 bước tính góc
- Mẹo nhớ và lưu ý
- VII. KẾT LUẬN
- Tổng kết
- Tài liệu tham khảo
I. GIỚI THIỆU
1. Góc giữa hai đường thẳng là gì?
Định nghĩa: Góc giữa hai đường thẳng là góc nhỏ nhất tạo bởi chúng khi cắt nhau hoặc khi song song với chúng cắt nhau.
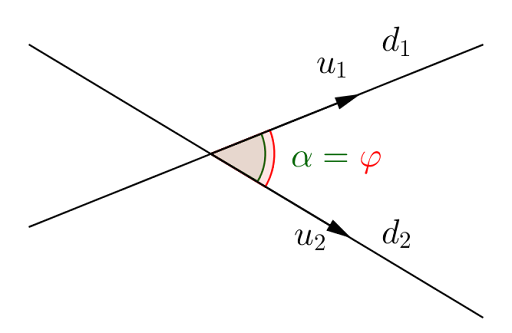
Đặc điểm quan trọng:
- Luôn lấy góc nhỏ hơn hoặc bằng 90°
- Nếu tính được góc > 90°, lấy góc bù: $\alpha = 180° – \alpha’$
Giá trị: $0° \leq \alpha \leq 90°$
2. Phân biệt với góc giữa hai vectơ
Đây là điểm khác biệt quan trọng cần nắm rõ:
- Góc giữa hai vectơ: Từ 0° đến 180°
- Góc giữa hai đường thẳng: Từ 0° đến 90° (chỉ lấy góc nhọn hoặc vuông)
3. Các trường hợp đặc biệt
- Góc 0°: Hai đường thẳng song song hoặc trùng nhau
- Góc 90°: Hai đường thẳng vuông góc
- Góc nhọn: $0° < \alpha < 90°$
4. Cấu trúc bài viết
Bài viết sẽ trình bày:
- Công thức trong mặt phẳng (2D) – 3 cách
- Công thức trong không gian (3D)
- 8 ví dụ minh họa
- 5 bài tập thực tế
- Bảng tổng hợp
II. CÔNG THỨC TRONG MẶT PHẲNG (2D)
CÁCH 1: Dùng hệ số góc (Đường thẳng dạng $y = ax + b$)
Điều kiện: Hai đường thẳng không song song với trục Oy
Cho hai đường thẳng:
- $d_1: y = k_1x + b_1$ (hệ số góc $k_1$)
- $d_2: y = k_2x + b_2$ (hệ số góc $k_2$)
Công thức:
$$\tan\alpha = \left|\frac{k_1 – k_2}{1 + k_1 k_2}\right|$$
Từ đó: $$\alpha = \arctan\left|\frac{k_1 – k_2}{1 + k_1 k_2}\right|$$
Chú ý:
- Nếu $k_1 k_2 = -1$ thì hai đường thẳng vuông góc ($\alpha = 90°$)
- Nếu $k_1 = k_2$ thì hai đường thẳng song song ($\alpha = 0°$)
Ví dụ 1: Tính góc giữa $d_1: y = 2x + 3$ và $d_2: y = -\frac{1}{2}x + 1$
Lời giải:
- $k_1 = 2$, $k_2 = -\frac{1}{2}$
- Kiểm tra: $k_1 \times k_2 = 2 \times (-\frac{1}{2}) = -1$
- Vậy $d_1 \perp d_2$ → $\alpha = 90°$
Ví dụ 2: Tính góc giữa $d_1: y = x + 1$ và $d_2: y = 2x – 3$
Lời giải:
- $k_1 = 1$, $k_2 = 2$
- $\tan\alpha = \left|\frac{1 – 2}{1 + 1 \times 2}\right| = \left|\frac{-1}{3}\right| = \frac{1}{3}$
- $\alpha = \arctan\left(\frac{1}{3}\right) \approx 18.43°$
CÁCH 2: Dùng vectơ chỉ phương
Vectơ chỉ phương (VTCP): Vectơ có giá trùng với đường thẳng
Cho hai đường thẳng:
- $d_1$ có VTCP $\vec{u_1} = (a_1; b_1)$
- $d_2$ có VTCP $\vec{u_2} = (a_2; b_2)$
Công thức:
$$\cos\alpha = \frac{|\vec{u_1} \cdot \vec{u_2}|}{|\vec{u_1}| \cdot |\vec{u_2}|}$$
$$\cos\alpha = \frac{|a_1 a_2 + b_1 b_2|}{\sqrt{a_1^2 + b_1^2} \cdot \sqrt{a_2^2 + b_2^2}}$$
Lưu ý: Dùng trị tuyệt đối để đảm bảo góc ≤ 90°
Cách xác định VTCP:
- Nếu phương trình tổng quát $ax + by + c = 0$: VTCP là $\vec{u} = (b; -a)$ hoặc $(-b; a)$
- Nếu phương trình tham số: $\begin{cases} x = x_0 + at \\ y = y_0 + bt \end{cases}$: VTCP là $\vec{u} = (a; b)$
- Nếu đi qua 2 điểm $A$, $B$: VTCP là $\vec{u} = \overrightarrow{AB}$
Ví dụ 3: Tính góc giữa $d_1: 2x + 3y – 1 = 0$ và $d_2: x – y + 2 = 0$
Lời giải:
- $d_1$ có VTCP: $\vec{u_1} = (3; -2)$ (hoặc $(-3; 2)$)
- $d_2$ có VTCP: $\vec{u_2} = (-1; -1)$ (hoặc $(1; 1)$)
- Tích vô hướng: $\vec{u_1} \cdot \vec{u_2} = 3 \times (-1) + (-2) \times (-1) = -3 + 2 = -1$
- $|\vec{u_1}| = \sqrt{9 + 4} = \sqrt{13}$
- $|\vec{u_2}| = \sqrt{1 + 1} = \sqrt{2}$
- $\cos\alpha = \frac{|-1|}{\sqrt{13} \times \sqrt{2}} = \frac{1}{\sqrt{26}}$
- $\alpha = \arccos\left(\frac{1}{\sqrt{26}}\right) \approx 78.69°$
CÁCH 3: Dùng vectơ pháp tuyến (VTPT)
Vectơ pháp tuyến: Vectơ vuông góc với đường thẳng
Cho hai đường thẳng:
- $d_1$ có VTPT $\vec{n_1} = (a_1; b_1)$
- $d_2$ có VTPT $\vec{n_2} = (a_2; b_2)$
Công thức:
$$\cos\alpha = \frac{|\vec{n_1} \cdot \vec{n_2}|}{|\vec{n_1}| \cdot |\vec{n_2}|}$$
$$\cos\alpha = \frac{|a_1 a_2 + b_1 b_2|}{\sqrt{a_1^2 + b_1^2} \cdot \sqrt{a_2^2 + b_2^2}}$$
Cách xác định VTPT:
- Nếu phương trình tổng quát $ax + by + c = 0$: VTPT là $\vec{n} = (a; b)$
- Nếu VTCP là $\vec{u} = (a; b)$: VTPT là $\vec{n} = (-b; a)$ hoặc $(b; -a)$
Ví dụ 4: Tính góc giữa $d_1: 3x – 4y + 5 = 0$ và $d_2: 5x + 12y – 7 = 0$
Lời giải:
- VTPT: $\vec{n_1} = (3; -4)$, $\vec{n_2} = (5; 12)$
- Tích vô hướng: $\vec{n_1} \cdot \vec{n_2} = 3 \times 5 + (-4) \times 12 = 15 – 48 = -33$
- $|\vec{n_1}| = \sqrt{9 + 16} = 5$
- $|\vec{n_2}| = \sqrt{25 + 144} = 13$
- $\cos\alpha = \frac{|-33|}{5 \times 13} = \frac{33}{65}$
- $\alpha = \arccos\left(\frac{33}{65}\right) \approx 59.49°$
So sánh 3 cách
| Phương pháp | Ưu điểm | Nhược điểm | Khi nào dùng |
|---|---|---|---|
| Hệ số góc | Đơn giản, trực quan | Không dùng cho đt song song Oy | Phương trình dạng $y = kx + b$ |
| VTCP | Linh hoạt, dùng được mọi TH | Cần xác định VTCP | Phương trình tham số hoặc qua 2 điểm |
| VTPT | Trực tiếp với PT tổng quát | Cần xác định VTPT | Phương trình dạng $ax + by + c = 0$ |
III. CÔNG THỨC TRONG KHÔNG GIAN (3D)
CÔNG THỨC TỔNG QUÁT
Trong không gian Oxyz, góc giữa hai đường thẳng luôn dùng vectơ chỉ phương
Cho hai đường thẳng:
- $d_1$ có VTCP $\vec{u_1} = (a_1; b_1; c_1)$
- $d_2$ có VTCP $\vec{u_2} = (a_2; b_2; c_2)$
Công thức:
$$\cos\alpha = \frac{|\vec{u_1} \cdot \vec{u_2}|}{|\vec{u_1}| \cdot |\vec{u_2}|}$$
$$\cos\alpha = \frac{|a_1 a_2 + b_1 b_2 + c_1 c_2|}{\sqrt{a_1^2 + b_1^2 + c_1^2} \cdot \sqrt{a_2^2 + b_2^2 + c_2^2}}$$
Lưu ý quan trọng:
- BẮT BUỘC dùng trị tuyệt đối để góc ≤ 90°
- Nếu không dùng trị tuyệt đối, có thể ra góc > 90°, phải lấy bù
Các dạng phương trình đường thẳng trong không gian
1. Phương trình tham số: $$d: \begin{cases} x = x_0 + a_1t \\ y = y_0 + b_1t \\ z = z_0 + c_1t \end{cases}$$
VTCP: $\vec{u} = (a_1; b_1; c_1)$
2. Phương trình chính tắc (không có mẫu = 0): $$d: \frac{x – x_0}{a_1} = \frac{y – y_0}{b_1} = \frac{z – z_0}{c_1}$$
VTCP: $\vec{u} = (a_1; b_1; c_1)$
3. Đường thẳng đi qua 2 điểm $A(x_1; y_1; z_1)$ và $B(x_2; y_2; z_2)$:
VTCP: $\vec{u} = \overrightarrow{AB} = (x_2 – x_1; y_2 – y_1; z_2 – z_1)$
Ví dụ minh họa
Ví dụ 5: Tính góc giữa hai đường thẳng:
- $d_1: \frac{x-1}{2} = \frac{y+1}{1} = \frac{z}{-1}$
- $d_2: \begin{cases} x = 1 + t \ y = 2 – t \ z = 3 + 2t \end{cases}$
Lời giải:
- VTCP: $\vec{u_1} = (2; 1; -1)$, $\vec{u_2} = (1; -1; 2)$
- Tích vô hướng: $\vec{u_1} \cdot \vec{u_2} = 2 \times 1 + 1 \times (-1) + (-1) \times 2 = 2 – 1 – 2 = -1$
- $|\vec{u_1}| = \sqrt{4 + 1 + 1} = \sqrt{6}$
- $|\vec{u_2}| = \sqrt{1 + 1 + 4} = \sqrt{6}$
- $\cos\alpha = \frac{|-1|}{\sqrt{6} \times \sqrt{6}} = \frac{1}{6}$
- $\alpha = \arccos\left(\frac{1}{6}\right) \approx 80.41°$
Ví dụ 6: Cho tứ diện ABCD với $A(1; 0; 0)$, $B(0; 1; 0)$, $C(0; 0; 1)$, $D(1; 1; 1)$. Tính góc giữa AB và CD.
Lời giải:
- $\overrightarrow{AB} = (-1; 1; 0)$
- $\overrightarrow{CD} = (1; 1; 0)$
- Tích vô hướng: $\overrightarrow{AB} \cdot \overrightarrow{CD} = (-1) \times 1 + 1 \times 1 + 0 \times 0 = 0$
- Vậy $AB \perp CD$ → $\alpha = 90°$
Lưu ý đặc biệt về trị tuyệt đối
Tại sao phải dùng trị tuyệt đối?
Vì góc giữa hai đường thẳng luôn ≤ 90°, nhưng góc giữa hai vectơ có thể > 90°.
Ví dụ minh họa:
- Nếu $\vec{u_1} \cdot \vec{u_2} = -3$ (âm) → góc giữa hai vectơ > 90°
- Nhưng góc giữa hai đường thẳng phải ≤ 90°
- Do đó dùng $|\vec{u_1} \cdot \vec{u_2}|$ để đảm bảo $\cos\alpha > 0$
So sánh:
- Không dùng trị tuyệt đối: $\cos\alpha = \frac{-3}{5} = -0.6$ → $\alpha = 126.87°$ (SAI)
- Dùng trị tuyệt đối: $\cos\alpha = \frac{|-3|}{5} = 0.6$ → $\alpha = 53.13°$ (ĐÚNG)
IV. CÁC TRƯỜNG HỢP ĐẶC BIỆT
1. Hai đường thẳng song song
Điều kiện:
- Mặt phẳng: $k_1 = k_2$ hoặc $\vec{u_1} = k\vec{u_2}$
- Không gian: $\vec{u_1} = k\vec{u_2}$ với $k > 0$
Góc: $\alpha = 0°$
Ví dụ 7:
- $d_1: 2x + 3y – 1 = 0$ có VTPT $(2; 3)$
- $d_2: 4x + 6y + 5 = 0$ có VTPT $(4; 6) = 2(2; 3)$
- $\Rightarrow d_1 \parallel d_2$ → $\alpha = 0°$
2. Hai đường thẳng vuông góc
Điều kiện:
- Mặt phẳng: $k_1 \times k_2 = -1$ hoặc $\vec{u_1} \cdot \vec{u_2} = 0$
- Không gian: $\vec{u_1} \cdot \vec{u_2} = 0$
Góc: $\alpha = 90°$
Ví dụ 8:
- $d_1: 3x – 2y + 1 = 0$ có VTPT $(3; -2)$
- $d_2: 2x + 3y – 5 = 0$ có VTPT $(2; 3)$
- Tích vô hướng: $3 \times 2 + (-2) \times 3 = 0$
- $\Rightarrow d_1 \perp d_2$ → $\alpha = 90°$
3. Góc giữa đường thẳng và trục tọa độ
Trục Ox: VTCP là $\vec{i} = (1; 0)$ (2D) hoặc $(1; 0; 0)$ (3D)
Trục Oy: VTCP là $\vec{j} = (0; 1)$ (2D) hoặc $(0; 1; 0)$ (3D)
Trục Oz: VTCP là $\vec{k} = (0; 0; 1)$ (3D)
Công thức nhanh:
- Góc với Ox: $\cos\alpha = \frac{|a_1|}{|\vec{u}|}$
- Góc với Oy: $\cos\alpha = \frac{|b_1|}{|\vec{u}|}$
- Góc với Oz: $\cos\alpha = \frac{|c_1|}{|\vec{u}|}$
V. BÀI TẬP THỰC TẾ
Bài tập 1: Góc nghiêng mái nhà
Đề bài: Mái nhà có dốc theo phương trình $y = -0.5x + 5$ (m). Mặt đất nằm ngang (trục Ox). Tính góc nghiêng của mái nhà.
Lời giải:
- Mái nhà: $y = -0.5x + 5$ → $k_1 = -0.5$
- Mặt đất (Ox): $y = 0$ → $k_2 = 0$
- $\tan\alpha = \left|\frac{-0.5 – 0}{1 + (-0.5) \times 0}\right| = |-0.5| = 0.5$
- $\alpha = \arctan(0.5) \approx 26.57°$
Ứng dụng: Thiết kế thoát nước, độ dốc chuẩn 18-30°.
Bài tập 2: Góc giao đường
Đề bài: Đường phố A có hướng $\vec{u_1} = (3; 4)$ m, đường phố B có hướng $\vec{u_2} = (1; 7)$ m. Tính góc giao nhau.
Lời giải:
- $\vec{u_1} \cdot \vec{u_2} = 3 \times 1 + 4 \times 7 = 31$
- $|\vec{u_1}| = 5$, $|\vec{u_2}| = \sqrt{50} = 5\sqrt{2}$
- $\cos\alpha = \frac{|31|}{5 \times 5\sqrt{2}} = \frac{31}{25\sqrt{2}}$
- $\alpha = \arccos\left(\frac{31}{25\sqrt{2}}\right) \approx 28.30°$
Ứng dụng: Thiết kế giao lộ, đèn tín hiệu.
Bài tập 3: Góc hàn trong kỹ thuật
Đề bài: Hai thanh kim loại nối với nhau:
- Thanh 1: phương trình $\frac{x-2}{1} = \frac{y-1}{2} = \frac{z}{1}$
- Thanh 2: phương trình $\frac{x}{2} = \frac{y-1}{1} = \frac{z-1}{-1}$
Tính góc hàn.
Lời giải:
- VTCP: $\vec{u_1} = (1; 2; 1)$, $\vec{u_2} = (2; 1; -1)$
- $\vec{u_1} \cdot \vec{u_2} = 1 \times 2 + 2 \times 1 + 1 \times (-1) = 3$
- $|\vec{u_1}| = \sqrt{6}$, $|\vec{u_2}| = \sqrt{6}$
- $\cos\alpha = \frac{|3|}{6} = 0.5$
- $\alpha = 60°$
Ứng dụng: Hàn kim loại, thiết kế khung kết cấu.
Bài tập 4: Ranh giới thửa đất
Đề bài: Thửa đất có hai cạnh ranh giới:
- Cạnh 1: qua $A(0; 0)$, $B(30; 40)$ m
- Cạnh 2: qua $A(0; 0)$, $C(50; 20)$ m
Tính góc tại đỉnh A.
Lời giải:
- $\overrightarrow{AB} = (30; 40)$, $\overrightarrow{AC} = (50; 20)$
- $\overrightarrow{AB} \cdot \overrightarrow{AC} = 30 \times 50 + 40 \times 20 = 2300$
- $|\overrightarrow{AB}| = 50$, $|\overrightarrow{AC}| = \sqrt{2900} = 10\sqrt{29}$
- $\cos\alpha = \frac{2300}{50 \times 10\sqrt{29}} = \frac{23}{5\sqrt{29}}$
- $\alpha = \arccos\left(\frac{23}{5\sqrt{29}}\right) \approx 31.33°$
Ứng dụng: Đo đạc địa chính, phân chia đất.
Bài tập 5: Góc bay máy bay
Đề bài: Máy bay A bay theo hướng $\vec{v_1} = (100; 50; 10)$ km/h, máy bay B bay theo $\vec{v_2} = (80; -60; 5)$ km/h. Tính góc giữa hai hướng bay.
Lời giải:
- $\vec{v_1} \cdot \vec{v_2} = 100 \times 80 + 50 \times (-60) + 10 \times 5 = 8000 – 3000 + 50 = 5050$
- $|\vec{v_1}| = \sqrt{10000 + 2500 + 100} = \sqrt{12600} \approx 112.25$
- $|\vec{v_2}| = \sqrt{6400 + 3600 + 25} = \sqrt{10025} \approx 100.12$
- $\cos\alpha = \frac{5050}{112.25 \times 100.12} \approx 0.449$
- $\alpha \approx 63.31°$
Ứng dụng: Kiểm soát không lưu, tránh va chạm.
VI. BẢNG TỔNG HỢP & MẸO NHỚ
Bảng công thức tổng hợp
| Không gian | Phương pháp | Công thức |
|---|---|---|
| Mặt phẳng | Hệ số góc | $\tan\alpha = \left|\frac{k_1 – k_2}{1 + k_1 k_2}\right|$ |
| Mặt phẳng | VTCP | $\cos\alpha = \frac{|\vec{u_1} \cdot \vec{u_2}|}{|\vec{u_1}| \cdot |\vec{u_2}|}$ |
| Mặt phẳng | VTPT | $\cos\alpha = \frac{|\vec{n_1} \cdot \vec{n_2}|}{|\vec{n_1}| \cdot |\vec{n_2}|}$ |
| Không gian | VTCP (duy nhất) | $\cos\alpha = \frac{|\vec{u_1} \cdot \vec{u_2}|}{|\vec{u_1}| \cdot |\vec{u_2}|}$ |
Bảng trường hợp đặc biệt
| Điều kiện | Góc | Tên gọi |
|---|---|---|
| $k_1 = k_2$ hoặc $\vec{u_1} = k\vec{u_2}$ | $0°$ | Song song |
| $k_1 k_2 = -1$ hoặc $\vec{u_1} \cdot \vec{u_2} = 0$ | $90°$ | Vuông góc |
| $0 < \alpha < 90°$ | Góc nhọn | Góc nhọn |
Quy trình 5 bước tính góc
Bước 1: Viết phương trình hai đường thẳng về dạng chuẩn
Bước 2: Xác định VTCP (hoặc VTPT hoặc hệ số góc)
Bước 3: Tính tích vô hướng (hoặc tính biểu thức tan)
Bước 4: Áp dụng công thức (NHỚ dùng trị tuyệt đối)
Bước 5: Tính góc bằng arccos hoặc arctan
Mẹo nhớ và lưu ý
Mẹo 1: Nhớ công thức nào dùng khi nào
- Phương trình $y = kx + b$ → Dùng hệ số góc
- Phương trình $ax + by + c = 0$ → Dùng VTPT
- Phương trình tham số hoặc qua 2 điểm → Dùng VTCP
Mẹo 2: Kiểm tra nhanh vuông góc
- 2D: $k_1 \times k_2 = -1$ hoặc tích vô hướng = 0
- 3D: Chỉ dùng tích vô hướng = 0
Mẹo 3: Trị tuyệt đối
- BẮT BUỘC khi tính góc giữa đường thẳng
- Không dùng khi tính góc giữa vectơ
Lưu ý quan trọng:
Góc giữa hai đường thẳng: $0° \leq \alpha \leq 90°$
Nếu tính được $\alpha > 90°$, lấy $180° – \alpha$
Trong không gian, chỉ dùng VTCP, không dùng VTPT
Luôn dùng trị tuyệt đối trong công thức
VII. KẾT LUẬN
Tổng kết
Bài viết đã hệ thống hóa công thức tính góc giữa hai đường thẳng:
Trong mặt phẳng (2D) – 3 phương pháp:
- Hệ số góc: $\tan\alpha = \left|\frac{k_1 – k_2}{1 + k_1 k_2}\right|$
- VTCP: $\cos\alpha = \frac{|\vec{u_1} \cdot \vec{u_2}|}{|\vec{u_1}| \cdot |\vec{u_2}|}$
- VTPT: $\cos\alpha = \frac{|\vec{n_1} \cdot \vec{n_2}|}{|\vec{n_1}| \cdot |\vec{n_2}|}$
Trong không gian (3D):
- Chỉ dùng VTCP với công thức tương tự 2D
Đặc điểm: Luôn lấy góc ≤ 90° (dùng trị tuyệt đối)
8 ví dụ lý thuyết + 5 bài tập thực tế
Ứng dụng: Kiến trúc, giao thông, kỹ thuật, địa chính
Tài liệu tham khảo
Xem thêm:
- Công thức góc giữa hai vectơ – Chi tiết
- Phương trình đường thẳng trong mặt phẳng và không gian
- Vị trí tương đối của hai đường thẳng

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
