Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ LỤC GIÁC ĐỀU
- 1. Lục giác đều là gì?
- 2. Tính chất đặc biệt
- II. CÔNG THỨC CHU VI LỤC GIÁC ĐỀU
- Công thức cơ bản – Theo cạnh
- Công thức khi biết bán kính đường tròn ngoại tiếp
- Công thức khi biết bán kính đường tròn nội tiếp
- III. CÔNG THỨC DIỆN TÍCH LỤC GIÁC ĐỀU
- CÔNG THỨC 1: Theo cạnh (Công thức chính)
- CÔNG THỨC 2: Theo bán kính ngoại tiếp
- CÔNG THỨC 3: Theo bán kính nội tiếp
- CÔNG THỨC 4: Theo đường chéo dài
- CÔNG THỨC 5: Theo chu vi
- Bảng tổng hợp công thức diện tích
- IV. CÁC CÔNG THỨC LIÊN QUAN
- 1. Góc trong lục giác đều
- 2. Bán kính đường tròn ngoại tiếp
- 3. Bán kính đường tròn nội tiếp
- 4. Độ dài đường chéo
- 5. Chiều cao tam giác đều thành phần
- 6. Diện tích tam giác đều thành phần
- 7. Số đường chéo
- V. BÀI TẬP THỰC TẾ
- VI. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức diện tích
- 2. Tính chất đặc biệt cần nhớ
- 3. Các sai lầm thường gặp
- 4. Các lời khuyên hữu ích
- 5. Quy trình giải bài tập chuẩn
- 6. Bảng công thức tóm tắt
- VII. KẾT LUẬN
- Tổng kết
- Tài liệu tham khảo và mở rộng
I. GIỚI THIỆU VỀ LỤC GIÁC ĐỀU
1. Lục giác đều là gì?
Định nghĩa: Lục giác đều là một đa giác đều có 6 cạnh bằng nhau và 6 góc bằng nhau. Đây là một trong những hình đa giác đều cơ bản và phổ biến nhất trong toán học và thiên nhiên.
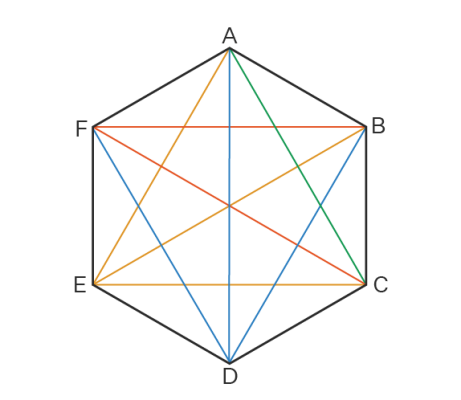
Tên gọi khác:
- Hexagon đều (Regular Hexagon) trong tiếng Anh
- Đa giác 6 cạnh đều
- Lục giác chính quy
Đặc điểm cơ bản:
- 6 cạnh: Tất cả các cạnh có độ dài bằng nhau (ký hiệu là $a$)
- 6 góc: Mỗi góc trong có số đo bằng nhau, đều bằng $120°$
- 6 đỉnh: Các đỉnh đều nằm trên một đường tròn ngoại tiếp
- Tổng các góc trong: $(6-2) \times 180° = 720°$
2. Tính chất đặc biệt
Tính đối xứng:
- 6 trục đối xứng:
- 3 trục nối 2 đỉnh đối diện (qua tâm)
- 3 trục nối trung điểm 2 cạnh đối diện (qua tâm)
- Tâm đối xứng: Có một tâm đối xứng duy nhất
Chia thành tam giác đều:
Một tính chất quan trọng và đẹp đẽ của lục giác đều: Khi nối tâm với các đỉnh, lục giác đều được chia thành 6 tam giác đều bằng nhau.
Điều này có nghĩa:
- Mỗi tam giác có cạnh bằng $a$
- Cả 6 tam giác đều có cùng diện tích
- Đây là cơ sở để tính diện tích lục giác đều
Liên quan đến đường tròn:
- Đường tròn ngoại tiếp:
- Bán kính $R$ từ tâm đến đỉnh
- Tính chất đặc biệt: $R = a$ (bán kính bằng cạnh!)
- Đường tròn nội tiếp:
- Bán kính $r$ từ tâm đến cạnh (vuông góc với cạnh)
- Công thức: $r = \frac{a\sqrt{3}}{2}$
II. CÔNG THỨC CHU VI LỤC GIÁC ĐỀU
Công thức cơ bản – Theo cạnh
Cho lục giác đều có cạnh $a$:
$$\boxed{P = 6a}$$
Giải thích:
- Lục giác đều có 6 cạnh bằng nhau
- Chu vi = Tổng độ dài 6 cạnh = $a + a + a + a + a + a = 6a$
Cách nhớ: “Sáu nhân cạnh”
Ví dụ 1: Tính chu vi lục giác đều có cạnh 5 cm
Lời giải:
- Cạnh: $a = 5$ cm
- Chu vi: $P = 6 \times 5 = 30$ cm
Kết luận: Chu vi lục giác đều là 30 cm.
Công thức khi biết bán kính đường tròn ngoại tiếp
Cho $R$ là bán kính đường tròn ngoại tiếp:
$$\boxed{P = 6R}$$
Lý do: Với lục giác đều, có tính chất đặc biệt là $R = a$ (bán kính ngoại tiếp bằng cạnh).
Chứng minh:
- Khi nối tâm O với hai đỉnh liên tiếp A và B, ta có tam giác OAB
- Do lục giác đều được chia thành 6 phần bằng nhau, góc ở tâm: $\widehat{AOB} = \frac{360°}{6} = 60°$
- Tam giác OAB có $OA = OB = R$ và $\widehat{AOB} = 60°$
- Vậy tam giác OAB là tam giác đều → $AB = OA = OB = R$
- Do đó: $a = R$
Ví dụ 2: Lục giác đều nội tiếp đường tròn bán kính 8 cm. Tính chu vi.
Lời giải:
- Bán kính ngoại tiếp: $R = 8$ cm
- Vì $R = a$ nên cạnh: $a = 8$ cm
- Chu vi: $P = 6 \times 8 = 48$ cm
Kết luận: Chu vi lục giác đều là 48 cm.
Công thức khi biết bán kính đường tròn nội tiếp
Cho $r$ là bán kính đường tròn nội tiếp:
$$\boxed{P = \frac{12r}{\sqrt{3}} = 4r\sqrt{3}}$$
Chứng minh:
- Từ công thức: $r = \frac{a\sqrt{3}}{2}$
- Suy ra: $a = \frac{2r}{\sqrt{3}} = \frac{2r\sqrt{3}}{3}$
- Chu vi: $P = 6a = 6 \times \frac{2r}{\sqrt{3}} = \frac{12r}{\sqrt{3}} = \frac{12r\sqrt{3}}{3} = 4r\sqrt{3}$
Ví dụ 3: Lục giác đều ngoại tiếp đường tròn bán kính $3\sqrt{3}$ cm. Tính chu vi.
Lời giải:
- Bán kính nội tiếp: $r = 3\sqrt{3}$ cm
- Chu vi: $P = 4 \times 3\sqrt{3} \times \sqrt{3} = 12 \times 3 = 36$ cm
Kết luận: Chu vi lục giác đều là 36 cm.
Cách khác:
- Tìm cạnh: $a = \frac{2r}{\sqrt{3}} = \frac{2 \times 3\sqrt{3}}{\sqrt{3}} = 6$ cm
- Chu vi: $P = 6 \times 6 = 36$ cm ✓
III. CÔNG THỨC DIỆN TÍCH LỤC GIÁC ĐỀU
CÔNG THỨC 1: Theo cạnh (Công thức chính)
Cho lục giác đều có cạnh $a$:
$$\boxed{S = \frac{3\sqrt{3}}{2}a^2}$$
Đây là công thức quan trọng nhất và được sử dụng nhiều nhất.
Chứng minh:
Phương pháp: Chia lục giác đều thành 6 tam giác đều.
Bước 1: Nối tâm O với 6 đỉnh, chia lục giác thành 6 tam giác đều, mỗi tam giác có cạnh $a$.
Bước 2: Diện tích một tam giác đều cạnh $a$: $$S_{\triangle} = \frac{a^2\sqrt{3}}{4}$$
Bước 3: Tổng diện tích 6 tam giác: $$S = 6 \times S_{\triangle} = 6 \times \frac{a^2\sqrt{3}}{4} = \frac{6a^2\sqrt{3}}{4} = \frac{3a^2\sqrt{3}}{2}$$
Cách nhớ: “Ba căn ba chia hai, nhân a bình phương”
Giá trị gần đúng: $\frac{3\sqrt{3}}{2} \approx 2.598$
Vậy: $S \approx 2.6a^2$
Ví dụ 4: Tính diện tích lục giác đều có cạnh 4 cm
Lời giải:
- Cạnh: $a = 4$ cm
- Áp dụng công thức: $$S = \frac{3\sqrt{3}}{2} \times 4^2 = \frac{3\sqrt{3}}{2} \times 16 = 24\sqrt{3}$$
- Giá trị gần đúng: $24\sqrt{3} \approx 24 \times 1.732 \approx 41.57$ cm²
Kết luận: Diện tích lục giác đều là $24\sqrt{3} \approx 41.57$ cm².
CÔNG THỨC 2: Theo bán kính ngoại tiếp
Cho $R$ là bán kính đường tròn ngoại tiếp:
$$\boxed{S = \frac{3\sqrt{3}}{2}R^2}$$
Lý do: Vì $R = a$ (tính chất đặc biệt của lục giác đều), nên công thức giống hệt công thức theo cạnh.
Ví dụ 5: Lục giác đều nội tiếp đường tròn bán kính 6 cm. Tính diện tích.
Lời giải:
- Bán kính ngoại tiếp: $R = 6$ cm
- Diện tích: $$S = \frac{3\sqrt{3}}{2} \times 6^2 = \frac{3\sqrt{3}}{2} \times 36 = 54\sqrt{3}$$
- Giá trị gần đúng: $54\sqrt{3} \approx 93.53$ cm²
Kết luận: Diện tích lục giác đều là $54\sqrt{3} \approx 93.53$ cm².
CÔNG THỨC 3: Theo bán kính nội tiếp
Cho $r$ là bán kính đường tròn nội tiếp:
$$\boxed{S = 2r^2\sqrt{3}}$$
Chứng minh:
Từ công thức $r = \frac{a\sqrt{3}}{2}$, ta suy ra: $$a^2 = \frac{4r^2}{3}$$
Thay vào công thức diện tích: $$S = \frac{3\sqrt{3}}{2} \times a^2 = \frac{3\sqrt{3}}{2} \times \frac{4r^2}{3} = \frac{4r^2\sqrt{3}}{2} = 2r^2\sqrt{3}$$
Ví dụ 6: Lục giác đều ngoại tiếp đường tròn bán kính $2\sqrt{3}$ cm. Tính diện tích.
Lời giải:
- Bán kính nội tiếp: $r = 2\sqrt{3}$ cm
- Diện tích: $$S = 2 \times (2\sqrt{3})^2 \times \sqrt{3} = 2 \times 12 \times \sqrt{3} = 24\sqrt{3}$$
- Giá trị gần đúng: $24\sqrt{3} \approx 41.57$ cm²
Kết luận: Diện tích lục giác đều là $24\sqrt{3} \approx 41.57$ cm².
CÔNG THỨC 4: Theo đường chéo dài
Đường chéo dài $d$ là đường chéo nối 2 đỉnh đối diện, đi qua tâm lục giác.
Mối quan hệ: $d = 2a$ (bằng 2 lần cạnh)
Công thức diện tích:
$$\boxed{S = \frac{3\sqrt{3}}{8}d^2}$$
Chứng minh:
- Từ $d = 2a$ suy ra $a = \frac{d}{2}$
- Thay vào công thức cơ bản: $$S = \frac{3\sqrt{3}}{2} \times a^2 = \frac{3\sqrt{3}}{2} \times \frac{d^2}{4} = \frac{3\sqrt{3}d^2}{8}$$
Ví dụ 7: Lục giác đều có đường chéo dài 10 cm. Tính diện tích.
Lời giải:
- Đường chéo dài: $d = 10$ cm
- Diện tích: $$S = \frac{3\sqrt{3}}{8} \times 10^2 = \frac{3\sqrt{3}}{8} \times 100 = \frac{300\sqrt{3}}{8} = \frac{75\sqrt{3}}{2}$$
- Giá trị gần đúng: $\frac{75\sqrt{3}}{2} \approx 64.95$ cm²
Kết luận: Diện tích lục giác đều là $\frac{75\sqrt{3}}{2} \approx 64.95$ cm².
CÔNG THỨC 5: Theo chu vi
Cho chu vi $P$:
$$\boxed{S = \frac{P^2\sqrt{3}}{24}}$$
Chứng minh:
- Từ $P = 6a$ suy ra $a = \frac{P}{6}$
- Thay vào công thức cơ bản: $$S = \frac{3\sqrt{3}}{2} \times a^2 = \frac{3\sqrt{3}}{2} \times \frac{P^2}{36} = \frac{3\sqrt{3}P^2}{72} = \frac{P^2\sqrt{3}}{24}$$
Ví dụ 8: Lục giác đều có chu vi 24 cm. Tính diện tích.
Lời giải:
- Chu vi: $P = 24$ cm
- Diện tích: $$S = \frac{24^2 \times \sqrt{3}}{24} = \frac{576\sqrt{3}}{24} = 24\sqrt{3}$$
- Giá trị gần đúng: $24\sqrt{3} \approx 41.57$ cm²
Kết luận: Diện tích lục giác đều là $24\sqrt{3} \approx 41.57$ cm².
Kiểm tra:
- Cạnh: $a = \frac{24}{6} = 4$ cm
- Diện tích: $S = \frac{3\sqrt{3}}{2} \times 16 = 24\sqrt{3}$ ✓
Bảng tổng hợp công thức diện tích
| Đại lượng cho trước | Công thức diện tích | Ghi chú |
|---|---|---|
| Cạnh $a$ | $S = \frac{3\sqrt{3}}{2}a^2$ | Công thức chính |
| Bán kính ngoại tiếp $R$ | $S = \frac{3\sqrt{3}}{2}R^2$ | Vì $R = a$ |
| Bán kính nội tiếp $r$ | $S = 2r^2\sqrt{3}$ | Rút gọn nhất |
| Đường chéo dài $d$ | $S = \frac{3\sqrt{3}}{8}d^2$ | $d = 2a$ |
| Chu vi $P$ | $S = \frac{P^2\sqrt{3}}{24}$ | Từ $P = 6a$ |
IV. CÁC CÔNG THỨC LIÊN QUAN
1. Góc trong lục giác đều
Công thức tính mỗi góc trong của đa giác đều $n$ cạnh:
$$\alpha = \frac{(n-2) \times 180°}{n}$$
Với lục giác đều ($n = 6$):
$$\boxed{\alpha = \frac{(6-2) \times 180°}{6} = \frac{4 \times 180°}{6} = \frac{720°}{6} = 120°}$$
Kết luận: Mỗi góc trong của lục giác đều bằng $120°$.
Tổng các góc trong: $6 \times 120° = 720°$
Kiểm tra: Công thức tổng góc trong đa giác $n$ cạnh: $(n-2) \times 180° = 4 \times 180° = 720°$ ✓
2. Bán kính đường tròn ngoại tiếp
Bán kính $R$ là khoảng cách từ tâm đến đỉnh của lục giác.
$$\boxed{R = a}$$
Đây là tính chất ĐẶC BIỆT và CỰC KỲ QUAN TRỌNG của lục giác đều:
- Bán kính đường tròn ngoại tiếp bằng đúng cạnh của lục giác
- Không có hình đa giác đều nào khác có tính chất này
Ý nghĩa: Khi nối tâm với các đỉnh, ta được 6 tam giác đều có cạnh bằng $a$.
3. Bán kính đường tròn nội tiếp
Bán kính $r$ là khoảng cách từ tâm đến cạnh (đường vuông góc).
$$\boxed{r = \frac{a\sqrt{3}}{2}}$$
Chứng minh:
- Xét tam giác đều OAB với $O$ là tâm, $A$, $B$ là hai đỉnh liên tiếp
- Chiều cao của tam giác đều cạnh $a$: $h = \frac{a\sqrt{3}}{2}$
- Bán kính nội tiếp $r$ chính là chiều cao này
Mối quan hệ với $R$:
$$r = R \times \frac{\sqrt{3}}{2}$$
Ví dụ: Nếu $a = 6$ cm thì:
- $R = 6$ cm
- $r = \frac{6\sqrt{3}}{2} = 3\sqrt{3} \approx 5.20$ cm
4. Độ dài đường chéo
Lục giác đều có 2 loại đường chéo khác nhau:
a) Đường chéo dài (nối 2 đỉnh đối diện, đi qua tâm):
$$\boxed{d_{\text{dài}} = 2a = 2R}$$
Giải thích: Đường chéo dài bằng đường kính của đường tròn ngoại tiếp.
b) Đường chéo ngắn (nối 2 đỉnh cách nhau 2 vị trí):
$$\boxed{d_{\text{ngắn}} = a\sqrt{3} = R\sqrt{3}}$$
Chứng minh:
- Xét tam giác tạo bởi 2 đỉnh và tâm
- Sử dụng định lý cosin hoặc tính chất hình học
Ví dụ 9: Lục giác đều có cạnh 6 cm. Tính độ dài các đường chéo.
Lời giải:
- Cạnh: $a = 6$ cm
- Đường chéo dài: $d_{\text{dài}} = 2 \times 6 = 12$ cm
- Đường chéo ngắn: $d_{\text{ngắn}} = 6\sqrt{3} \approx 10.39$ cm
Kết luận:
- Đường chéo dài: 12 cm
- Đường chéo ngắn: $6\sqrt{3} \approx 10.39$ cm
5. Chiều cao tam giác đều thành phần
Khi chia lục giác đều thành 6 tam giác đều, mỗi tam giác có:
Chiều cao:
$$\boxed{h = \frac{a\sqrt{3}}{2} = r}$$
Lưu ý: Chiều cao của tam giác đều thành phần chính bằng bán kính đường tròn nội tiếp.
6. Diện tích tam giác đều thành phần
Diện tích mỗi tam giác đều cạnh $a$:
$$\boxed{S_{\triangle} = \frac{a^2\sqrt{3}}{4}}$$
Quan hệ với diện tích lục giác:
$$S_{\text{lục giác}} = 6 \times S_{\triangle} = 6 \times \frac{a^2\sqrt{3}}{4} = \frac{3\sqrt{3}}{2}a^2$$
7. Số đường chéo
Công thức tổng quát cho đa giác $n$ cạnh:
$$\text{Số đường chéo} = \frac{n(n-3)}{2}$$
Với lục giác đều ($n = 6$):
$$\text{Số đường chéo} = \frac{6 \times (6-3)}{2} = \frac{6 \times 3}{2} = 9$$
Kết luận: Lục giác đều có 9 đường chéo.
Phân loại:
- 3 đường chéo dài (qua tâm)
- 6 đường chéo ngắn (không qua tâm)
V. BÀI TẬP THỰC TẾ
Bài tập 1: Tổ ong
Đề bài: Một ô trong tổ ong có dạng lục giác đều với cạnh 0.5 cm.
a) Tính chu vi một ô tổ ong b) Tính diện tích một ô tổ ong c) Nếu một mảng tổ có 100 ô, tính tổng diện tích mảng tổ
Lời giải:
Câu a) Chu vi một ô:
- Cạnh: $a = 0.5$ cm
- Chu vi: $P = 6 \times 0.5 = 3$ cm
Câu b) Diện tích một ô: $$S = \frac{3\sqrt{3}}{2} \times (0.5)^2 = \frac{3\sqrt{3}}{2} \times 0.25 = \frac{3\sqrt{3}}{8}$$ $$S \approx 0.65 \text{ cm}^2$$
Câu c) Tổng diện tích 100 ô: $$S_{\text{tổng}} = 100 \times 0.65 = 65 \text{ cm}^2$$
Kết luận:
- Chu vi một ô: 3 cm
- Diện tích một ô: $\frac{3\sqrt{3}}{8} \approx 0.65$ cm²
- Tổng diện tích 100 ô: 65 cm²
Ứng dụng: Nghiên cứu sinh học ong, thiết kế kết cấu tổ ong trong kỹ thuật, kiến trúc sinh học.
Bài tập 2: Gạch lục giác lát nền
Đề bài: Một viên gạch lục giác đều có cạnh 20 cm. Cần lát nền cho phòng hình chữ nhật có kích thước 4m × 5m. Hỏi cần bao nhiêu viên gạch? (Bỏ qua phần thừa và khe hở)
Lời giải:
Bước 1: Tính diện tích phòng
- Kích thước phòng: 4m × 5m
- Diện tích phòng: $4 \times 5 = 20$ m² = $200,000$ cm²
Bước 2: Tính diện tích một viên gạch
- Cạnh: $a = 20$ cm
- Diện tích: $$S_{\text{gạch}} = \frac{3\sqrt{3}}{2} \times 20^2 = \frac{3\sqrt{3}}{2} \times 400 = 600\sqrt{3}$$ $$S_{\text{gạch}} \approx 1039.2 \text{ cm}^2$$
Bước 3: Tính số viên gạch cần dùng $$\text{Số viên} = \frac{200,000}{1039.2} \approx 192.5$$
Làm tròn lên: Cần khoảng 193 viên gạch
Kết luận: Cần mua khoảng 193 viên gạch (nên mua 200 viên để dự phòng).
Ứng dụng: Tính toán vật liệu xây dựng, thiết kế nội thất, dự toán chi phí thi công.
Bài tập 3: Đai ốc lục giác
Đề bài: Một đai ốc có dạng lục giác đều. Khoảng cách giữa 2 cạnh đối diện (đường kính của đường tròn nội tiếp) là 12 mm.
a) Tính bán kính đường tròn nội tiếp b) Tính độ dài cạnh đai ốc c) Tính diện tích mặt cắt ngang của đai ốc
Lời giải:
Câu a) Bán kính nội tiếp:
- Đường kính nội tiếp: $2r = 12$ mm
- Bán kính nội tiếp: $r = 6$ mm
Câu b) Tính cạnh đai ốc:
Từ công thức $r = \frac{a\sqrt{3}}{2}$, suy ra: $$a = \frac{2r}{\sqrt{3}} = \frac{2 \times 6}{\sqrt{3}} = \frac{12}{\sqrt{3}} = \frac{12\sqrt{3}}{3} = 4\sqrt{3}$$ $$a \approx 6.93 \text{ mm}$$
Câu c) Diện tích mặt cắt: $$S = 2r^2\sqrt{3} = 2 \times 36 \times \sqrt{3} = 72\sqrt{3}$$ $$S \approx 124.7 \text{ mm}^2$$
Kết luận:
- Bán kính nội tiếp: 6 mm
- Cạnh đai ốc: $4\sqrt{3} \approx 6.93$ mm
- Diện tích: $72\sqrt{3} \approx 124.7$ mm²
Ứng dụng: Kỹ thuật cơ khí, thiết kế linh kiện máy móc, chế tạo đai ốc bu lông.
Bài tập 4: Thiết kế sân vườn
Đề bài: Một khu vườn có dạng lục giác đều với chu vi 48 mét.
a) Tính độ dài cạnh và diện tích khu vườn b) Chi phí làm cỏ là 50,000 đồng/m². Tính tổng chi phí
Lời giải:
Câu a) Tính cạnh và diện tích:
- Chu vi: $P = 48$ m
- Cạnh: $a = \frac{P}{6} = \frac{48}{6} = 8$ m
- Diện tích: $$S = \frac{3\sqrt{3}}{2} \times 8^2 = \frac{3\sqrt{3}}{2} \times 64 = 96\sqrt{3}$$ $$S \approx 166.3 \text{ m}^2$$
Câu b) Tính chi phí: $$\text{Chi phí} = 166.3 \times 50,000 = 8,315,000 \text{ đồng}$$
Kết luận:
- Cạnh khu vườn: 8 m
- Diện tích: $96\sqrt{3} \approx 166.3$ m²
- Tổng chi phí làm cỏ: 8,315,000 đồng
Ứng dụng: Thiết kế cảnh quan, quy hoạch công viên, dự toán chi phí thi công sân vườn.
Bài tập 5: Game hex grid
Đề bài: Trong một game chiến thuật, bản đồ sử dụng lưới lục giác đều, mỗi ô có cạnh 1 đơn vị. Tính diện tích vùng đất gồm 7 ô (1 ô trung tâm + 6 ô xung quanh).
Lời giải:
Bước 1: Diện tích một ô $$S_1 = \frac{3\sqrt{3}}{2} \times 1^2 = \frac{3\sqrt{3}}{2}$$
Bước 2: Diện tích 7 ô $$S_7 = 7 \times \frac{3\sqrt{3}}{2} = \frac{21\sqrt{3}}{2}$$ $$S_7 \approx 18.19 \text{ đơn vị}^2$$
Kết luận: Diện tích vùng đất 7 ô là $\frac{21\sqrt{3}}{2} \approx 18.19$ đơn vị vuông.
Ứng dụng: Thiết kế game chiến thuật (Civilization, Catan), lập trình game, tính toán phạm vi ảnh hưởng.
Bài tập 6: Tấm pin mặt trời
Đề bài: Một tấm pin mặt trời có dạng lục giác đều. Đường chéo dài của tấm pin là 80 cm. Tính diện tích thu năng lượng của tấm pin.
Lời giải:
- Đường chéo dài: $d = 80$ cm
- Áp dụng công thức: $$S = \frac{3\sqrt{3}}{8} \times d^2 = \frac{3\sqrt{3}}{8} \times 80^2$$ $$= \frac{3\sqrt{3}}{8} \times 6400 = \frac{19200\sqrt{3}}{8} = 2400\sqrt{3}$$ $$S \approx 4156.9 \text{ cm}^2 = 0.416 \text{ m}^2$$
Kết luận: Diện tích thu năng lượng là $2400\sqrt{3} \approx 4156.9$ cm² = 0.416 m².
Ứng dụng: Năng lượng tái tạo, tính toán công suất pin mặt trời, thiết kế hệ thống năng lượng.
Bài tập 7: Thiết kế logo
Đề bài: Logo của một công ty có dạng lục giác đều nội tiếp trong đường tròn bán kính 5 cm. Tính diện tích phần logo cần in.
Lời giải:
- Bán kính ngoại tiếp: $R = 5$ cm
- Vì $R = a$ nên cạnh: $a = 5$ cm
- Diện tích logo: $$S = \frac{3\sqrt{3}}{2} \times 5^2 = \frac{3\sqrt{3}}{2} \times 25 = \frac{75\sqrt{3}}{2}$$ $$S \approx 64.95 \text{ cm}^2$$
Kết luận: Diện tích logo cần in là $\frac{75\sqrt{3}}{2} \approx 64.95$ cm².
Ứng dụng: Thiết kế đồ họa, branding, tính toán chi phí in ấn, thiết kế logo thương hiệu.
VI. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức diện tích
Khẩu quyết chính:
“Ba căn ba chia hai, nhân a bình phương”
$$S = \frac{3\sqrt{3}}{2}a^2$$
Cách nhớ số:
Hệ số $\frac{3\sqrt{3}}{2}$ có giá trị gần đúng: $$\frac{3\sqrt{3}}{2} \approx 2.598 \approx 2.6$$
Vậy: $S \approx 2.6a^2$
Mẹo kiểm tra nhanh: Diện tích lục giác đều gấp khoảng 2.6 lần bình phương cạnh.
Cách nhớ thứ hai:
Lục giác đều = 6 tam giác đều
$$S = 6 \times \frac{a^2\sqrt{3}}{4} = \frac{6a^2\sqrt{3}}{4} = \frac{3a^2\sqrt{3}}{2}$$
2. Tính chất đặc biệt cần nhớ
$R = a$ – Bán kính ngoại tiếp bằng cạnh (duy nhất lục giác đều!)
$r = \frac{a\sqrt{3}}{2}$ – Bán kính nội tiếp
Góc trong = 120° – Mỗi góc đều 120 độ
Chia thành 6 tam giác đều – Tất cả bằng nhau, cạnh $a$
Đường chéo dài = $2a$, đường chéo ngắn = $a\sqrt{3}$
Có 9 đường chéo – 3 dài + 6 ngắn
3. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm công thức với tam giác đều
Sai:
- Diện tích lục giác = $\frac{a^2\sqrt{3}}{4}$ ❌
Đúng:
- Diện tích tam giác đều = $\frac{a^2\sqrt{3}}{4}$
- Diện tích lục giác đều = $\frac{3\sqrt{3}}{2}a^2$ ✓
❌ SAI LẦM 2: Quên hệ số $\frac{3\sqrt{3}}{2}$
Sai:
- $S = a^2$ hoặc $S = 3a^2$ ❌
Đúng:
- $S = \frac{3\sqrt{3}}{2}a^2$ ✓
- Phải có cả hệ số $3$, $\sqrt{3}$ và $\frac{1}{2}$
❌ SAI LẦM 3: Nhầm bán kính ngoại tiếp và nội tiếp
Cần nhớ rõ:
- $R$ (ngoại tiếp) = từ tâm đến đỉnh = $a$
- $r$ (nội tiếp) = từ tâm đến cạnh = $\frac{a\sqrt{3}}{2}$
- $R > r$ (luôn luôn)
❌ SAI LẦM 4: Tính sai đường chéo
Nhầm lẫn:
- Nghĩ tất cả đường chéo đều bằng nhau ❌
Sự thật:
- Có 2 loại: dài ($2a$) và ngắn ($a\sqrt{3}$) ✓
4. Các lời khuyên hữu ích
Luôn vẽ hình để hình dung lục giác đều và các yếu tố
Ghi nhớ tính chất $R = a$ – Đây là chìa khóa của nhiều bài toán
Kiểm tra đơn vị – Chu vi (cm), diện tích (cm²)
Dùng giá trị gần đúng $\sqrt{3} \approx 1.732$ để ước lượng kết quả
Phân biệt rõ $R$ và $r$ – Vẽ cả hai đường tròn để thấy sự khác biệt
5. Quy trình giải bài tập chuẩn
Bước 1: Đọc kỹ đề, xác định đại lượng đã cho
- Cạnh $a$?
- Bán kính $R$ hay $r$?
- Chu vi $P$?
- Đường chéo $d$?
Bước 2: Chọn công thức phù hợp
- Xem bảng tổng hợp công thức
- Chọn công thức trực tiếp hoặc gián tiếp
Bước 3: Thay số và tính toán
- Thay số cẩn thận
- Chú ý dấu ngoặc, phép tính
Bước 4: Đơn giản hóa
- Rút gọn biểu thức (nếu có $\sqrt{3}$)
- Tính giá trị gần đúng (nếu cần)
Bước 5: Kiểm tra và kết luận
- Đơn vị có đúng không?
- Kết quả có hợp lý không?
- Viết kết luận đầy đủ
6. Bảng công thức tóm tắt
| Công thức | Biểu thức | Ghi chú |
|---|---|---|
| Chu vi | $P = 6a$ | 6 lần cạnh |
| Diện tích (cạnh) | $S = \frac{3\sqrt{3}}{2}a^2$ | Công thức chính |
| Diện tích ($R$) | $S = \frac{3\sqrt{3}}{2}R^2$ | Vì $R = a$ |
| Diện tích ($r$) | $S = 2r^2\sqrt{3}$ | Rút gọn |
| Diện tích ($d$) | $S = \frac{3\sqrt{3}}{8}d^2$ | Theo đường chéo dài |
| Diện tích ($P$) | $S = \frac{P^2\sqrt{3}}{24}$ | Theo chu vi |
| Bán kính ngoại tiếp | $R = a$ | Đặc biệt! |
| Bán kính nội tiếp | $r = \frac{a\sqrt{3}}{2}$ | Chiều cao tam giác |
| Đường chéo dài | $d_{\text{dài}} = 2a$ | Qua tâm |
| Đường chéo ngắn | $d_{\text{ngắn}} = a\sqrt{3}$ | Không qua tâm |
| Góc trong | $\alpha = 120°$ | Mỗi góc |
| Số đường chéo | 9 | 3 dài + 6 ngắn |
VII. KẾT LUẬN
Tổng kết
Bài viết đã trình bày hệ thống công thức lục giác đều đầy đủ và chi tiết:
Công thức chu vi:
- Cơ bản: $P = 6a$
- Theo $R$: $P = 6R$
- Theo $r$: $P = 4r\sqrt{3}$
Công thức diện tích:
- Công thức chính: $S = \frac{3\sqrt{3}}{2}a^2$
- Theo $R$: $S = \frac{3\sqrt{3}}{2}R^2$
- Theo $r$: $S = 2r^2\sqrt{3}$
- Theo đường chéo: $S = \frac{3\sqrt{3}}{8}d^2$
- Theo chu vi: $S = \frac{P^2\sqrt{3}}{24}$
Tính chất đặc biệt:
- Bán kính ngoại tiếp: $R = a$ (quan trọng nhất!)
- Bán kính nội tiếp: $r = \frac{a\sqrt{3}}{2}$
- Góc trong: $120°$
- Chia thành 6 tam giác đều
7 bài tập thực tế ứng dụng:
- Tổ ong, gạch lát nền, đai ốc
- Sân vườn, game, pin mặt trời, logo
Tài liệu tham khảo và mở rộng
Các chủ đề liên quan:
- [Công Thức Tam Giác Đều – Diện Tích và Chu Vi]
- [Công Thức Đa Giác Đều – Tổng Quát n Cạnh]
- [Công Thức Hình Học Phẳng – Tổng Hợp]
- [Lát Mặt Phẳng Với Đa Giác Đều]
- [Đường Tròn Nội Tiếp và Ngoại Tiếp]
- [Kết Cấu Tổ Ong Trong Kỹ Thuật]

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
