Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ TAM GIÁC ĐỀU
- 1. Định nghĩa tam giác đều
- 2. Tính chất đặc biệt
- 3. Ký hiệu thường dùng
- II. CÔNG THỨC CƠ BẢN VỀ TAM GIÁC ĐỀU
- 1. Công thức đường cao
- 2. Công thức diện tích
- 3. Công thức chu vi
- 4. Công thức bán kính đường tròn ngoại tiếp
- 5. Công thức bán kính đường tròn nội tiếp
- III. BẢNG CÔNG THỨC TỔNG HỢP
- Bảng công thức đầy đủ theo cạnh a
- Các công thức ngược (tìm a từ đại lượng khác)
- Liên hệ giữa các đại lượng
- IV. LƯU Ý VỀ "THỂ TÍCH TAM GIÁC ĐỀU"
- 1. Làm rõ khái niệm
- 2. Các khái niệm liên quan (có thể tích)
- 3. Kết luận phân biệt
- V. BÀI TẬP MẪU
- VI. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Lưu ý quan trọng
- VII. KẾT LUẬN
I. GIỚI THIỆU VỀ TAM GIÁC ĐỀU
1. Định nghĩa tam giác đều
Tam giác đều là tam giác đặc biệt có các tính chất sau:
Về cạnh: Ba cạnh bằng nhau $$AB = BC = CA = a$$
Về góc: Ba góc bằng nhau và mỗi góc bằng 60° $$\angle A = \angle B = \angle C = 60°$$
Hình minh họa:
A
/|\
/ | \
a / |h \ a
/ | \
/____|____\
B a C
Đặc điểm nhận dạng:
- Chỉ cần biết một cạnh là biết toàn bộ tam giác
- Là hình có tính đối xứng hoàn hảo nhất trong các tam giác
2. Tính chất đặc biệt
Tam giác đều có những tính chất rất đẹp và đặc biệt:
Về hình học:
- Là tam giác cân đặc biệt, cân tại cả ba đỉnh
- Là tam giác đều và đối xứng hoàn toàn
- Có ba trục đối xứng (ba đường cao)
Về góc:
- Mỗi góc trong = 60°
- Mỗi góc ngoài = 120°
Về các đường đặc biệt:
- Đường cao = Đường trung tuyến = Đường phân giác = Đường trung trực
- Ba đường cao đồng quy tại một điểm
- Ba đường trung tuyến đồng quy tại một điểm
- Ba đường phân giác đồng quy tại một điểm
Về tâm:
- Trọng tâm = Trực tâm = Tâm đường tròn ngoại tiếp = Tâm đường tròn nội tiếp
- Tất cả các tâm đều trùng nhau tại một điểm duy nhất
3. Ký hiệu thường dùng
| Ký hiệu | Ý nghĩa | Đơn vị thường dùng |
|---|---|---|
| a | Độ dài cạnh tam giác đều | cm, m, dm |
| h | Đường cao (= đường trung tuyến) | cm, m, dm |
| S | Diện tích tam giác | cm², m², dm² |
| P | Chu vi tam giác | cm, m, dm |
| R | Bán kính đường tròn ngoại tiếp | cm, m, dm |
| r | Bán kính đường tròn nội tiếp | cm, m, dm |
Lưu ý: Trong tam giác đều, chỉ cần biết một đại lượng (ví dụ: cạnh a) là có thể tính được tất cả các đại lượng khác.
II. CÔNG THỨC CƠ BẢN VỀ TAM GIÁC ĐỀU
1. Công thức đường cao
📌 Công thức:
$$\boxed{h = \frac{a\sqrt{3}}{2}}$$
Trong đó:
- $h$: đường cao của tam giác đều
- $a$: độ dài cạnh tam giác đều
Chứng minh:
Phương pháp: Sử dụng định lý Pythagore
Bước 1: Trong tam giác đều ABC, kẻ đường cao AH từ đỉnh A xuống cạnh BC.
Bước 2: Do tam giác đều nên đường cao AH cũng là đường trung tuyến, do đó: $$BH = HC = \frac{a}{2}$$
Bước 3: Xét tam giác vuông ABH:
- Cạnh huyền: $AB = a$
- Cạnh góc vuông: $BH = \frac{a}{2}$
- Cạnh góc vuông: $AH = h$ (cần tìm)
Bước 4: Áp dụng định lý Pythagore: $$AB^2 = AH^2 + BH^2$$
$$a^2 = h^2 + \left(\frac{a}{2}\right)^2$$
$$a^2 = h^2 + \frac{a^2}{4}$$
$$h^2 = a^2 – \frac{a^2}{4} = \frac{4a^2 – a^2}{4} = \frac{3a^2}{4}$$
$$h = \frac{a\sqrt{3}}{2}$$ ✓
Ví dụ 1: Tam giác đều có cạnh $a = 6$ cm. Tính đường cao.
Lời giải:
Áp dụng công thức: $$h = \frac{a\sqrt{3}}{2} = \frac{6\sqrt{3}}{2} = 3\sqrt{3} \text{ cm}$$
Kết luận: Đường cao $h = 3\sqrt{3} \approx 5.196$ cm.
2. Công thức diện tích
📌 Công thức:
$$\boxed{S = \frac{a^2\sqrt{3}}{4}}$$
Đây là công thức QUAN TRỌNG NHẤT của tam giác đều!
Chứng minh:
Phương pháp: Sử dụng công thức diện tích tam giác thông thường
Bước 1: Diện tích tam giác tổng quát: $$S = \frac{1}{2} \times \text{đáy} \times \text{cao}$$
Bước 2: Trong tam giác đều:
- Đáy = $a$
- Cao = $h = \frac{a\sqrt{3}}{2}$
Bước 3: Thay vào công thức: $$S = \frac{1}{2} \times a \times \frac{a\sqrt{3}}{2}$$
$$S = \frac{a \times a\sqrt{3}}{4}$$
$$S = \frac{a^2\sqrt{3}}{4}$$ ✓
Ví dụ 2: Tam giác đều có cạnh $a = 4$ cm. Tính diện tích.
Lời giải:
Áp dụng công thức: $$S = \frac{a^2\sqrt{3}}{4} = \frac{4^2\sqrt{3}}{4} = \frac{16\sqrt{3}}{4} = 4\sqrt{3} \text{ cm}^2$$
Kết luận: Diện tích $S = 4\sqrt{3} \approx 6.928$ cm².
Lưu ý quan trọng:
⚠️ Công thức này cần nhớ thuộc lòng vì:
- Xuất hiện rất nhiều trong bài tập
- Là cơ sở để tính các đại lượng khác
- Không thể suy ra nhanh trong phòng thi
⚠️ Dễ nhầm: Đừng nhầm thành $\frac{a^2\sqrt{3}}{2}$ (thiếu mẫu số 4)
3. Công thức chu vi
📌 Công thức:
$$\boxed{P = 3a}$$
Giải thích: Chu vi tam giác đều bằng 3 lần độ dài cạnh (vì ba cạnh bằng nhau).
Ví dụ 3: Tam giác đều có cạnh $a = 5$ cm. Tính chu vi.
Lời giải: $$P = 3a = 3 \times 5 = 15 \text{ cm}$$
Kết luận: Chu vi $P = 15$ cm.
4. Công thức bán kính đường tròn ngoại tiếp
📌 Công thức:
$$\boxed{R = \frac{a\sqrt{3}}{3} = \frac{a}{\sqrt{3}}}$$
Hai dạng viết tương đương:
- Dạng rút gọn: $R = \frac{a\sqrt{3}}{3}$
- Dạng chưa rút gọn: $R = \frac{a}{\sqrt{3}}$
Liên hệ với đường cao:
$$R = \frac{2h}{3} = \frac{2}{3} \times \frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{3}$$
Ý nghĩa: Bán kính ngoại tiếp bằng $\frac{2}{3}$ đường cao.
Chứng minh:
Phương pháp 1: Dùng định lý sin
Trong tam giác bất kỳ: $$\frac{a}{\sin A} = 2R$$
Trong tam giác đều, $A = 60°$ nên: $$\frac{a}{\sin 60°} = 2R$$
$$\frac{a}{\frac{\sqrt{3}}{2}} = 2R$$
$$\frac{2a}{\sqrt{3}} = 2R$$
$$R = \frac{a}{\sqrt{3}} = \frac{a\sqrt{3}}{3}$$ ✓
Phương pháp 2: Dùng tính chất trọng tâm
Trong tam giác đều, tâm đường tròn ngoại tiếp trùng với trọng tâm. Trọng tâm cách đỉnh một khoảng bằng $\frac{2}{3}$ đường cao:
$$R = \frac{2h}{3} = \frac{2}{3} \times \frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{3}$$ ✓
Ví dụ 4: Tam giác đều có cạnh $a = 3$ cm. Tính bán kính đường tròn ngoại tiếp.
Lời giải: $$R = \frac{a\sqrt{3}}{3} = \frac{3\sqrt{3}}{3} = \sqrt{3} \text{ cm}$$
Kết luận: $R = \sqrt{3} \approx 1.732$ cm.
5. Công thức bán kính đường tròn nội tiếp
📌 Công thức:
$$\boxed{r = \frac{a\sqrt{3}}{6} = \frac{a}{2\sqrt{3}}}$$
Liên hệ với đường cao:
$$r = \frac{h}{3} = \frac{1}{3} \times \frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{6}$$
Ý nghĩa: Bán kính nội tiếp bằng $\frac{1}{3}$ đường cao.
Liên hệ với bán kính ngoại tiếp:
$$\boxed{r = \frac{R}{2}}$$
Đây là công thức rất quan trọng để kiểm tra kết quả!
Chứng minh:
Phương pháp: Dùng công thức diện tích
Diện tích tam giác bằng chu vi nhân bán kính nội tiếp chia đôi: $$S = \frac{1}{2} \times P \times r$$
Thay vào: $$\frac{a^2\sqrt{3}}{4} = \frac{1}{2} \times 3a \times r$$
$$\frac{a^2\sqrt{3}}{4} = \frac{3ar}{2}$$
$$r = \frac{a^2\sqrt{3}}{4} \times \frac{2}{3a}$$
$$r = \frac{a\sqrt{3}}{6}$$ ✓
Ví dụ 5: Tam giác đều có cạnh $a = 6$ cm. Tính bán kính đường tròn nội tiếp.
Lời giải: $$r = \frac{a\sqrt{3}}{6} = \frac{6\sqrt{3}}{6} = \sqrt{3} \text{ cm}$$
Kiểm tra: Với $a = 6$ cm, ta có:
- $R = \frac{6\sqrt{3}}{3} = 2\sqrt{3}$ cm
- $r = \sqrt{3}$ cm
- Thật vậy: $R = 2r$ → $2\sqrt{3} = 2 \times \sqrt{3}$ ✓
Kết luận: $r = \sqrt{3} \approx 1.732$ cm.
III. BẢNG CÔNG THỨC TỔNG HỢP
Bảng công thức đầy đủ theo cạnh a
| Đại lượng | Công thức | Dạng khác | Giá trị xấp xỉ (với a = 1) |
|---|---|---|---|
| Đường cao | $h = \frac{a\sqrt{3}}{2}$ | $h \approx 0.866a$ | 0.866 |
| Diện tích | $S = \frac{a^2\sqrt{3}}{4}$ | $S \approx 0.433a^2$ | 0.433 |
| Chu vi | $P = 3a$ | – | 3 |
| Bán kính ngoại tiếp | $R = \frac{a\sqrt{3}}{3}$ | $R = \frac{a}{\sqrt{3}} \approx 0.577a$ | 0.577 |
| Bán kính nội tiếp | $r = \frac{a\sqrt{3}}{6}$ | $r = \frac{a}{2\sqrt{3}} \approx 0.289a$ | 0.289 |
Ghi nhớ: Tất cả các công thức (trừ chu vi) đều có chứa $\sqrt{3}$.
Các công thức ngược (tìm a từ đại lượng khác)
Nếu biết đường cao h, tìm a:
$$\boxed{a = \frac{2h}{\sqrt{3}} = \frac{2h\sqrt{3}}{3}}$$
Ví dụ: Biết $h = 3\sqrt{3}$ cm, tìm $a$? $$a = \frac{2 \times 3\sqrt{3}}{\sqrt{3}} = 6 \text{ cm}$$
Nếu biết diện tích S, tìm a:
$$\boxed{a = \sqrt{\frac{4S}{\sqrt{3}}} = 2\sqrt{\frac{S}{\sqrt{3}}}}$$
Hoặc dạng đơn giản hơn: $$a^2 = \frac{4S}{\sqrt{3}} \Rightarrow a = \sqrt{\frac{4S}{\sqrt{3}}}$$
Ví dụ: Biết $S = 9\sqrt{3}$ cm², tìm $a$? $$\frac{a^2\sqrt{3}}{4} = 9\sqrt{3}$$ $$a^2 = 36$$ $$a = 6 \text{ cm}$$
Nếu biết bán kính ngoại tiếp R, tìm a:
$$\boxed{a = R\sqrt{3}}$$
Ví dụ: Biết $R = 2\sqrt{3}$ cm, tìm $a$? $$a = 2\sqrt{3} \times \sqrt{3} = 2 \times 3 = 6 \text{ cm}$$
Nếu biết bán kính nội tiếp r, tìm a:
$$\boxed{a = 2r\sqrt{3}}$$
Ví dụ: Biết $r = \sqrt{3}$ cm, tìm $a$? $$a = 2 \times \sqrt{3} \times \sqrt{3} = 2 \times 3 = 6 \text{ cm}$$
Liên hệ giữa các đại lượng
Quan hệ giữa R và r: $$\boxed{R = 2r}$$
Bán kính ngoại tiếp gấp đôi bán kính nội tiếp.
Quan hệ giữa h và r: $$\boxed{h = 3r}$$
Đường cao gấp ba lần bán kính nội tiếp.
Quan hệ giữa h và R: $$\boxed{h = \frac{3R}{2}}$$
Đường cao bằng $\frac{3}{2}$ bán kính ngoại tiếp.
Bảng tóm tắt:
| Quan hệ | Công thức |
|---|---|
| $R$ và $r$ | $R = 2r$ |
| $h$ và $r$ | $h = 3r$ |
| $h$ và $R$ | $h = \frac{3R}{2}$ |
| $R$ và $a$ | $R = \frac{a\sqrt{3}}{3}$ |
| $r$ và $a$ | $r = \frac{a\sqrt{3}}{6}$ |
IV. LƯU Ý VỀ “THỂ TÍCH TAM GIÁC ĐỀU”
1. Làm rõ khái niệm
⚠️ LƯU Ý CỰC KỲ QUAN TRỌNG:
TAM GIÁC ĐỀU LÀ HÌNH PHẲNG 2 CHIỀU → KHÔNG CÓ THỂ TÍCH!
Tam giác đều CHỈ CÓ:
- ✅ Diện tích (đơn vị: cm², m²)
- ✅ Chu vi (đơn vị: cm, m)
Tam giác đều KHÔNG CÓ:
- ❌ Thể tích (không phải hình khối 3D)
Giải thích:
- Thể tích chỉ áp dụng cho vật thể ba chiều (khối)
- Tam giác đều nằm trong mặt phẳng, chỉ có hai chiều (dài và rộng)
- Do đó không thể tính thể tích cho tam giác đều
2. Các khái niệm liên quan (có thể tích)
Một số hình khối liên quan đến tam giác đều CÓ THỂ TÍCH:
a) Lăng trụ đứng đáy tam giác đều:
Hình minh họa:
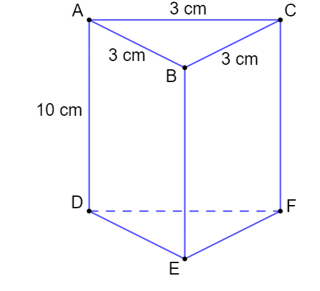
Công thức thể tích: $$\boxed{V = S_{\text{đáy}} \times h_{\text{lăng trụ}} = \frac{a^2\sqrt{3}}{4} \times h}$$
Trong đó:
- $a$: cạnh đáy tam giác đều
- $h$: chiều cao của lăng trụ (khoảng cách giữa hai đáy)
- $S_{\text{đáy}} = \frac{a^2\sqrt{3}}{4}$: diện tích tam giác đều đáy
Ví dụ: Lăng trụ đứng đáy tam giác đều cạnh 4 cm, chiều cao 10 cm. $$V = \frac{4^2\sqrt{3}}{4} \times 10 = 4\sqrt{3} \times 10 = 40\sqrt{3} \text{ cm}^3$$
b) Tứ diện đều (cạnh a):
Hình minh họa:
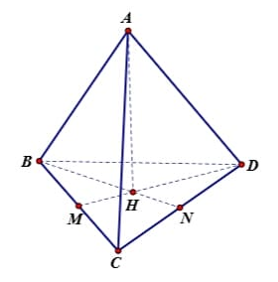
Tứ diện đều là hình không gian có 4 mặt đều là tam giác đều bằng nhau.
Công thức thể tích: $$\boxed{V = \frac{a^3\sqrt{2}}{12}}$$
Đường cao tứ diện đều: $$h = \frac{a\sqrt{6}}{3}$$
Diện tích toàn phần: $$S_{tp} = 4 \times \frac{a^2\sqrt{3}}{4} = a^2\sqrt{3}$$
Ví dụ: Tứ diện đều cạnh $a = 6$ cm. $$V = \frac{6^3\sqrt{2}}{12} = \frac{216\sqrt{2}}{12} = 18\sqrt{2} \text{ cm}^3$$
3. Kết luận phân biệt
| Hình | Số chiều | Có diện tích? | Có thể tích? |
|---|---|---|---|
| Tam giác đều | 2D (phẳng) | ✅ Có: $S = \frac{a^2\sqrt{3}}{4}$ | ❌ Không |
| Lăng trụ đáy tam giác đều | 3D (khối) | ✅ Có (diện tích xung quanh, toàn phần) | ✅ Có: $V = \frac{a^2\sqrt{3}}{4} \times h$ |
| Tứ diện đều | 3D (khối) | ✅ Có (diện tích toàn phần) | ✅ Có: $V = \frac{a^3\sqrt{2}}{12}$ |
Ghi nhớ:
- Tam giác đều: chỉ có diện tích
- Lăng trụ/Tứ diện: có cả diện tích và thể tích
V. BÀI TẬP MẪU
Dạng 1: Tính đường cao
Đề bài: Cho tam giác đều có cạnh $a = 8$ cm. Tính đường cao của tam giác.
Lời giải:
Áp dụng công thức đường cao: $$h = \frac{a\sqrt{3}}{2} = \frac{8\sqrt{3}}{2} = 4\sqrt{3} \text{ cm}$$
Kết luận: Đường cao $h = 4\sqrt{3} \approx 6.928$ cm.
Dạng 2: Tính diện tích
Đề bài: Cho tam giác đều có cạnh $a = 6$ cm. Tính diện tích tam giác.
Lời giải:
Áp dụng công thức diện tích: $$S = \frac{a^2\sqrt{3}}{4} = \frac{6^2\sqrt{3}}{4} = \frac{36\sqrt{3}}{4} = 9\sqrt{3} \text{ cm}^2$$
Kết luận: Diện tích $S = 9\sqrt{3} \approx 15.588$ cm².
Dạng 3: Tìm cạnh khi biết diện tích
Đề bài: Cho tam giác đều có diện tích $S = 16\sqrt{3}$ cm². Tính độ dài cạnh $a$.
Lời giải:
Từ công thức diện tích: $$S = \frac{a^2\sqrt{3}}{4}$$
Thay số: $$16\sqrt{3} = \frac{a^2\sqrt{3}}{4}$$
Nhân cả hai vế với 4: $$64\sqrt{3} = a^2\sqrt{3}$$
Chia cả hai vế cho $\sqrt{3}$: $$a^2 = 64$$
$$a = 8 \text{ cm}$$
Kết luận: Cạnh tam giác đều $a = 8$ cm.
Dạng 4: Tính bán kính ngoại tiếp và nội tiếp
Đề bài: Cho tam giác đều có cạnh $a = 9$ cm. Tính bán kính đường tròn ngoại tiếp $R$ và bán kính đường tròn nội tiếp $r$.
Lời giải:
Tính R: $$R = \frac{a\sqrt{3}}{3} = \frac{9\sqrt{3}}{3} = 3\sqrt{3} \text{ cm}$$
Tính r: $$r = \frac{a\sqrt{3}}{6} = \frac{9\sqrt{3}}{6} = \frac{3\sqrt{3}}{2} \text{ cm}$$
Kiểm tra: $R = 2r$? $$3\sqrt{3} = 2 \times \frac{3\sqrt{3}}{2} = 3\sqrt{3}$$ ✓
Kết luận:
- Bán kính ngoại tiếp: $R = 3\sqrt{3} \approx 5.196$ cm
- Bán kính nội tiếp: $r = \frac{3\sqrt{3}}{2} \approx 2.598$ cm
Dạng 5: Bài toán ngược – Tìm cạnh từ đường cao
Đề bài: Cho tam giác đều có đường cao $h = 5\sqrt{3}$ cm. Tính độ dài cạnh $a$.
Lời giải:
Từ công thức đường cao: $$h = \frac{a\sqrt{3}}{2}$$
Thay số: $$5\sqrt{3} = \frac{a\sqrt{3}}{2}$$
Nhân cả hai vế với 2: $$10\sqrt{3} = a\sqrt{3}$$
Chia cả hai vế cho $\sqrt{3}$: $$a = 10 \text{ cm}$$
Kết luận: Cạnh tam giác đều $a = 10$ cm.
Dạng 6: Thể tích lăng trụ đứng đáy tam giác đều
Đề bài: Một lăng trụ đứng có đáy là tam giác đều cạnh $a = 4$ cm, chiều cao lăng trụ $h = 10$ cm. Tính thể tích lăng trụ.
Lời giải:
Bước 1: Tính diện tích đáy (tam giác đều): $$S_{\text{đáy}} = \frac{a^2\sqrt{3}}{4} = \frac{4^2\sqrt{3}}{4} = \frac{16\sqrt{3}}{4} = 4\sqrt{3} \text{ cm}^2$$
Bước 2: Tính thể tích lăng trụ: $$V = S_{\text{đáy}} \times h = 4\sqrt{3} \times 10 = 40\sqrt{3} \text{ cm}^3$$
Kết luận: Thể tích lăng trụ $V = 40\sqrt{3} \approx 69.28$ cm³.
VI. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Đường cao:
“Cạnh nhân căn ba chia hai”
$$h = \frac{a\sqrt{3}}{2}$$
Cách nhớ: Lấy cạnh $a$, nhân với $\sqrt{3}$, rồi chia cho 2.
Diện tích:
“Cạnh bình nhân căn ba chia bốn”
$$S = \frac{a^2\sqrt{3}}{4}$$
Cách nhớ: Bình phương cạnh $a^2$, nhân $\sqrt{3}$, chia 4.
⚠️ Chú ý: Đây là công thức dễ nhầm nhất! Nhớ kỹ mẫu số là 4, không phải 2.
Bán kính ngoại tiếp:
“Cạnh chia căn ba” hoặc “Cạnh nhân căn ba chia ba”
$$R = \frac{a}{\sqrt{3}} = \frac{a\sqrt{3}}{3}$$
Cách nhớ: Lấy cạnh $a$ chia cho $\sqrt{3}$ (hoặc nhân $\sqrt{3}$ rồi chia 3).
Bán kính nội tiếp:
“Bằng nửa R” hoặc “Cạnh nhân căn ba chia sáu”
$$r = \frac{R}{2} = \frac{a\sqrt{3}}{6}$$
Cách nhớ: Nếu nhớ được $R$ thì $r = \frac{R}{2}$ (đơn giản nhất).
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm công thức diện tích
Sai: $S = \frac{a^2\sqrt{3}}{2}$ ❌
Đúng: $S = \frac{a^2\sqrt{3}}{4}$ ✓
Giải thích: Thiếu mẫu số 4 là sai lầm rất phổ biến!
❌ SAI LẦM 2: Quên rút gọn $\frac{a}{\sqrt{3}}$
Chưa chuẩn: $R = \frac{a}{\sqrt{3}}$ (còn căn ở mẫu)
Chuẩn: $R = \frac{a\sqrt{3}}{3}$ ✓ (đã khử mẫu)
Cách khử mẫu: Nhân cả tử và mẫu với $\sqrt{3}$ $$\frac{a}{\sqrt{3}} = \frac{a \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{a\sqrt{3}}{3}$$
❌ SAI LẦM 3: Nghĩ tam giác đều có thể tích
Sai: “Thể tích tam giác đều = …” ❌
Đúng: Tam giác đều KHÔNG CÓ thể tích, chỉ có diện tích! ✓
Nhớ: Chỉ hình khối 3D mới có thể tích.
❌ SAI LẦM 4: Nhầm $R = r$
Sai: $R = r$ ❌
Đúng: $R = 2r$ ✓
Nhớ: Bán kính ngoại tiếp gấp đôi bán kính nội tiếp.
3. Lưu ý quan trọng
Số $\sqrt{3}$ xuất hiện trong TẤT CẢ công thức (trừ chu vi $P = 3a$)
Tam giác đều đặc biệt: Trọng tâm = Trực tâm = Tâm ngoại tiếp = Tâm nội tiếp (tất cả trùng nhau!)
Góc trong tam giác đều = 60°:
- $\sin 60° = \frac{\sqrt{3}}{2}$
- $\cos 60° = \frac{1}{2}$
- $\tan 60° = \sqrt{3}$
Khi làm bài tập, luôn kiểm tra: $R = 2r$ để đảm bảo tính đúng
Đơn vị:
- Cạnh, đường cao, bán kính: cm, m, dm
- Diện tích: cm², m², dm²
- Thể tích (nếu là khối): cm³, m³, dm³
VII. KẾT LUẬN
Bài viết đã trình bày đầy đủ các công thức về tam giác đều cạnh a:
Đường cao: $$h = \frac{a\sqrt{3}}{2}$$
Diện tích: ← CÔNG THỨC QUAN TRỌNG NHẤT $$S = \frac{a^2\sqrt{3}}{4}$$
Chu vi: $$P = 3a$$
Bán kính đường tròn ngoại tiếp: $$R = \frac{a\sqrt{3}}{3} = \frac{a}{\sqrt{3}}$$
Bán kính đường tròn nội tiếp: $$r = \frac{a\sqrt{3}}{6} = \frac{R}{2}$$
Bài tập mẫu: 6 dạng có lời giải chi tiết
Đặc điểm nhận dạng tam giác đều
Đặc điểm công thức:
- ✨ Tất cả công thức (trừ chu vi) đều chứa $\sqrt{3}$
- ✨ Đơn giản, dễ nhớ, dễ áp dụng
- ✨ Liên hệ chặt chẽ: $R = 2r$, $h = 3r$, $h = \frac{3R}{2}$
Đặc điểm hình học:
- 3 cạnh bằng nhau
- 3 góc bằng nhau (mỗi góc 60°)
- Các tâm trùng nhau
Lời khuyên học tập
📌 Học thuộc 2 công thức cốt lõi: Diện tích và đường cao
📌 Nhớ kỹ: Tam giác đều KHÔNG CÓ thể tích (chỉ có diện tích)
📌 Ghi nhớ công thức kiểm tra: $R = 2r$ (để tự kiểm tra kết quả)
📌 Luyện tập tính ngược: Từ $S$, $h$, $R$, $r$ → tìm cạnh $a$
📌 Phân biệt rõ:
- Tam giác đều: có diện tích
- Lăng trụ đáy tam giác đều: có thể tích
- Tứ diện đều: có thể tích
📌 Vẽ hình minh họa: Giúp hình dung và nhớ lâu hơn
📌 Làm nhiều bài tập: Từ cơ bản đến nâng cao để thành thạo

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
