Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ HÌNH VIÊN PHÂN
- 1. Định nghĩa hình viên phân
- 2. Các yếu tố cơ bản
- 3. Phân loại viên phân
- II. CÔNG THỨC DIỆN TÍCH HÌNH VIÊN PHÂN ⭐
- 1. Công thức tổng quát (Dùng góc ở tâm)
- 2. Phân tích công thức
- 3. Công thức khi góc tính bằng độ
- 4. Ví dụ minh họa chi tiết
- 5. Công thức khi biết chiều cao $h$
- 6. Công thức khi biết dây cung $l$
- III. CÔNG THỨC CHIỀU CAO VIÊN PHÂN
- 1. Định nghĩa chiều cao
- 2. Công thức tính chiều cao
- 3. Ví dụ minh họa
- 4. Mối quan hệ giữa $h$, $R$, $l$
- IV. CÔNG THỨC CHU VI VIÊN PHÂN
- 1. Định nghĩa chu vi
- 2. Công thức tính chu vi
- 3. Ví dụ minh họa
- V. CÁC TRƯỜNG HỢP ĐẶC BIỆT
- 1. Nửa hình tròn (Góc 180°)
- 2. Viên phân góc 60°
- 3. Viên phân góc 90°
- 4. Viên phân góc 120°
- 5. Bảng các giá trị thường gặp
- VI. BẢNG TỔNG HỢP CÔNG THỨC ⭐
- Bảng 1: Công thức chính (Quan trọng nhất)
- Bảng 2: Mối quan hệ các đại lượng
- Bảng 3: Công thức bổ sung
- VII. PHƯƠNG PHÁP GIẢI BÀI TẬP
- Phương pháp 1: Biết $R$ và góc $\alpha$
- Phương pháp 2: Biết $R$ và chiều cao $h$
- Phương pháp 3: Biết $R$ và dây cung $l$
- VIII. BÀI TẬP MẪU
- Bài tập 1: Dạng cơ bản – Biết R và góc
- Bài tập 2: Biết R và dây cung
- Bài tập 3: Biết R và chiều cao
- Bài tập 4: Bài toán thực tế – Cửa sổ
- IX. KẾT LUẬN
- Công thức QUAN TRỌNG NHẤT ⭐
- Quy tắc vàng khi giải bài
I. GIỚI THIỆU VỀ HÌNH VIÊN PHÂN
1. Định nghĩa hình viên phân
Hình viên phân (còn gọi là hình phân giác hoặc segment) là một hình phẳng đặc biệt trong hình học, được tạo thành bởi hai thành phần:
- Một cung tròn – phần đường tròn giới hạn bởi hai điểm
- Một dây cung – đoạn thẳng nối hai đầu mút của cung đó
Nói cách khác: Hình viên phân là phần hình tròn nằm giữa một dây cung và cung tròn tương ứng với dây cung đó.
Hình dung: Khi cắt một quả cam theo đường không qua tâm, phần nhỏ được cắt ra có dạng hình viên phân.
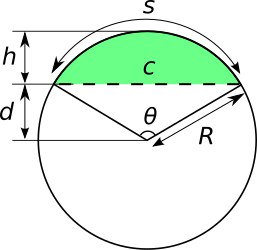
2. Các yếu tố cơ bản
Để xác định và tính toán các đại lượng của hình viên phân, ta cần nắm rõ các yếu tố sau:
Tâm đường tròn: Điểm $O$ – trung tâm của đường tròn chứa viên phân
Bán kính: $R$ – khoảng cách từ tâm $O$ đến bất kỳ điểm nào trên đường tròn
Dây cung: Đoạn thẳng $AB$ nối hai đầu mút của cung, độ dài ký hiệu là $l$
Cung tròn: $\widehat{AB}$ – phần đường tròn nối A và B
Góc ở tâm: $\alpha$ (alpha) – góc $\widehat{AOB}$ tạo bởi hai bán kính $OA$ và $OB$
- Đơn vị: radian (rad) hoặc độ (°)
- Phạm vi: $0 < \alpha < 2\pi$ (hoặc $0° < \alpha < 360°$)
Chiều cao viên phân: $h$ – khoảng cách vuông góc từ điểm giữa cung đến dây cung (còn gọi là độ cao của viên phân)
3. Phân loại viên phân
Dựa vào góc ở tâm, hình viên phân được chia thành các loại:
Viên phân nhỏ (Minor segment):
- Góc ở tâm: $\alpha < \pi$ rad (tức $\alpha < 180°$)
- Diện tích nhỏ hơn nửa hình tròn
- Là loại viên phân thường gặp nhất
Viên phân lớn (Major segment):
- Góc ở tâm: $\alpha > \pi$ rad (tức $\alpha > 180°$)
- Diện tích lớn hơn nửa hình tròn
- Ít gặp trong thực tế
Nửa hình tròn (Semicircle):
- Góc ở tâm: $\alpha = \pi$ rad (tức $\alpha = 180°$)
- Dây cung là đường kính
- Trường hợp đặc biệt của viên phân
II. CÔNG THỨC DIỆN TÍCH HÌNH VIÊN PHÂN ⭐
1. Công thức tổng quát (Dùng góc ở tâm)
Đây là công thức quan trọng nhất và hay sử dụng nhất khi tính diện tích hình viên phân:
NGUYÊN TẮC CƠ BẢN:
$$\boxed{S_{\text{viên phân}} = S_{\text{quạt}} – S_{\text{tam giác}}}$$
Ý nghĩa: Diện tích viên phân bằng diện tích hình quạt tròn trừ đi diện tích tam giác $OAB$.
CÔNG THỨC CHI TIẾT:
$$\boxed{S = \frac{R^2}{2}(\alpha – \sin\alpha)}$$
Trong đó:
- $S$: diện tích hình viên phân (đơn vị: cm², m²,…)
- $R$: bán kính đường tròn
- $\alpha$: góc ở tâm (đơn vị RADIAN – rất quan trọng!)
Cách nhớ: “Diện tích viên phân = Diện tích hình quạt – Diện tích tam giác”
Điều kiện áp dụng:
- $0 < \alpha < 2\pi$ (trong hệ radian)
- $\alpha$ phải tính bằng radian khi áp dụng công thức
2. Phân tích công thức
Để hiểu rõ công thức trên, ta phân tích thành hai phần:
Phần 1: Diện tích hình quạt tròn $OAB$
Hình quạt tròn là hình giới hạn bởi hai bán kính $OA$, $OB$ và cung $\widehat{AB}$.
Công thức: $$S_{\text{quạt}} = \frac{R^2\alpha}{2}$$
Giải thích:
- Diện tích toàn bộ hình tròn: $\pi R^2$
- Hình quạt chiếm tỉ lệ $\frac{\alpha}{2\pi}$ của hình tròn
- Vậy $S_{\text{quạt}} = \pi R^2 \cdot \frac{\alpha}{2\pi} = \frac{R^2\alpha}{2}$
Phần 2: Diện tích tam giác $OAB$
Tam giác $OAB$ có hai cạnh bằng $R$ (là hai bán kính) và góc xen giữa là $\alpha$.
Công thức: $$S_{\text{tam giác}} = \frac{1}{2} \cdot R \cdot R \cdot \sin\alpha = \frac{R^2\sin\alpha}{2}$$
Tổng hợp:
Do viên phân nằm giữa cung và dây cung, ta có: $$S_{\text{viên phân}} = S_{\text{quạt}} – S_{\text{tam giác}}$$ $$= \frac{R^2\alpha}{2} – \frac{R^2\sin\alpha}{2}$$ $$= \frac{R^2}{2}(\alpha – \sin\alpha)$$
3. Công thức khi góc tính bằng độ
Trong thực tế, góc thường được cho bằng độ (°) thay vì radian. Khi đó, ta cần chuyển đổi.
Công thức chuyển đổi:
Để đổi từ độ sang radian: $$\alpha_{\text{(rad)}} = \alpha_{\text{(độ)}} \times \frac{\pi}{180}$$
Ví dụ:
- $60° = 60 \times \frac{\pi}{180} = \frac{\pi}{3}$ rad
- $90° = 90 \times \frac{\pi}{180} = \frac{\pi}{2}$ rad
- $180° = 180 \times \frac{\pi}{180} = \pi$ rad
Quy trình tính toán:
Bước 1: Chuyển góc từ độ sang radian: $$\alpha_{\text{(rad)}} = \alpha_{\text{(độ)}} \times \frac{\pi}{180}$$
Bước 2: Áp dụng công thức: $$S = \frac{R^2}{2}\left(\alpha_{\text{(rad)}} – \sin\alpha_{\text{(độ)}}\right)$$
Chú ý: Khi tính $\sin\alpha$, dùng máy tính ở chế độ DEG (độ)
CÔNG THỨC TRỰC TIẾP KHI DÙNG ĐỘ:
$$\boxed{S = \frac{\pi R^2 \alpha_{\text{(độ)}}}{360} – \frac{R^2\sin\alpha_{\text{(độ)}}}{2}}$$
Công thức này tiện lợi khi không muốn chuyển đổi sang radian.
4. Ví dụ minh họa chi tiết
Ví dụ 1: Tính diện tích viên phân có bán kính $R = 6$ cm và góc ở tâm $\alpha = 60°$
Lời giải:
Cách 1: Chuyển sang radian
Bước 1: Chuyển đổi góc $$\alpha = 60° = 60 \times \frac{\pi}{180} = \frac{\pi}{3} \text{ rad}$$
Bước 2: Tính $\sin 60°$ $$\sin 60° = \frac{\sqrt{3}}{2}$$
Bước 3: Áp dụng công thức $$S = \frac{R^2}{2}(\alpha – \sin\alpha)$$ $$= \frac{36}{2}\left(\frac{\pi}{3} – \frac{\sqrt{3}}{2}\right)$$ $$= 18\left(\frac{\pi}{3} – \frac{\sqrt{3}}{2}\right)$$ $$= 6\pi – 9\sqrt{3}$$
Bước 4: Tính giá trị số $$S \approx 18.85 – 15.59 = \boxed{3.26 \text{ cm}^2}$$
Cách 2: Dùng công thức độ trực tiếp
$$S = \frac{\pi \cdot 36 \cdot 60}{360} – \frac{36 \cdot \frac{\sqrt{3}}{2}}{2}$$ $$= \frac{2160\pi}{360} – \frac{18\sqrt{3}}{2}$$ $$= 6\pi – 9\sqrt{3}$$ $$\approx \boxed{3.26 \text{ cm}^2}$$
Ví dụ 2: Viên phân có bán kính $R = 10$ cm và góc ở tâm $\alpha = 90°$. Tính diện tích.
Lời giải:
Bước 1: Chuyển đổi góc $$\alpha = 90° = \frac{\pi}{2} \text{ rad}$$
Bước 2: Tính $\sin 90°$ $$\sin 90° = 1$$
Bước 3: Áp dụng công thức $$S = \frac{100}{2}\left(\frac{\pi}{2} – 1\right)$$ $$= 50\left(\frac{\pi}{2} – 1\right)$$ $$= 25\pi – 50$$
Bước 4: Tính giá trị số $$S \approx 78.54 – 50 = \boxed{28.54 \text{ cm}^2}$$
Ví dụ 3: Viên phân có bán kính $R = 8$ cm và góc ở tâm $\alpha = 120°$. Tính diện tích.
Lời giải:
Bước 1: Chuyển đổi $$\alpha = 120° = \frac{2\pi}{3} \text{ rad}$$
Bước 2: Tính $\sin 120°$ $$\sin 120° = \sin(180° – 60°) = \sin 60° = \frac{\sqrt{3}}{2}$$
Bước 3: Áp dụng công thức $$S = \frac{64}{2}\left(\frac{2\pi}{3} – \frac{\sqrt{3}}{2}\right)$$ $$= 32\left(\frac{2\pi}{3} – \frac{\sqrt{3}}{2}\right)$$ $$= \frac{64\pi}{3} – 16\sqrt{3}$$
Bước 4: Tính giá trị $$S \approx 67.02 – 27.71 = \boxed{39.31 \text{ cm}^2}$$
5. Công thức khi biết chiều cao $h$
Trong một số bài toán, ta không biết góc $\alpha$ mà chỉ biết chiều cao viên phân $h$.
Phương pháp:
Bước 1: Tính góc $\alpha$ từ chiều cao
Từ công thức chiều cao (sẽ trình bày chi tiết ở phần III): $$h = R(1 – \cos\frac{\alpha}{2})$$
Suy ra: $$\cos\frac{\alpha}{2} = \frac{R – h}{R}$$
$$\frac{\alpha}{2} = \arccos\left(\frac{R – h}{R}\right)$$
$$\alpha = 2\arccos\left(\frac{R – h}{R}\right)$$
Bước 2: Áp dụng công thức diện tích thông thường
CÔNG THỨC TRỰC TIẾP (Phức tạp hơn):
Nếu không muốn tính góc, có thể dùng công thức:
$$\boxed{S = R^2 \arccos\frac{R-h}{R} – (R-h)\sqrt{2Rh – h^2}}$$
Công thức này khó nhớ hơn nhưng tiện lợi khi máy tính có sẵn.
6. Công thức khi biết dây cung $l$
Khi biết bán kính $R$ và độ dài dây cung $l = AB$:
Phương pháp:
Bước 1: Tính góc từ dây cung
Trong tam giác $OAB$ cân tại $O$, kẻ đường cao từ $O$ xuống $AB$ tại trung điểm $H$.
Ta có: $$AH = \frac{l}{2}$$
Trong tam giác vuông $OAH$: $$\sin\frac{\alpha}{2} = \frac{AH}{OA} = \frac{l/2}{R} = \frac{l}{2R}$$
Suy ra: $$\frac{\alpha}{2} = \arcsin\frac{l}{2R}$$
$$\alpha = 2\arcsin\frac{l}{2R}$$
Bước 2: Tính diện tích
Thay $\alpha$ vào công thức diện tích thông thường.
Điều kiện: $l \leq 2R$ (dây cung không thể dài hơn đường kính)
III. CÔNG THỨC CHIỀU CAO VIÊN PHÂN
1. Định nghĩa chiều cao
Chiều cao viên phân (ký hiệu $h$) là khoảng cách vuông góc từ điểm giữa cung tròn xuống dây cung.
Cách xác định:
- Lấy điểm $M$ là điểm giữa của cung $\widehat{AB}$
- Kẻ đường vuông góc từ $M$ xuống dây cung $AB$, cắt $AB$ tại $H$
- Độ dài $MH$ chính là chiều cao $h$
Tính chất:
- $H$ là trung điểm của dây cung $AB$
- $O$, $M$, $H$ thẳng hàng
- $h = OM – OH = R – OH$
2. Công thức tính chiều cao
Công thức 1 (Khi biết $R$ và góc $\alpha$):
$$\boxed{h = R\left(1 – \cos\frac{\alpha}{2}\right)}$$
Chứng minh:
Trong tam giác vuông $OHA$ (với $H$ là trung điểm $AB$): $$OH = OA \cdot \cos\frac{\alpha}{2} = R\cos\frac{\alpha}{2}$$
Chiều cao: $$h = OM – OH = R – R\cos\frac{\alpha}{2} = R\left(1 – \cos\frac{\alpha}{2}\right)$$
Công thức 2 (Khi biết $R$ và độ dài dây cung $l$):
$$\boxed{h = R – \sqrt{R^2 – \frac{l^2}{4}}}$$
Chứng minh:
Trong tam giác vuông $OHA$: $$OH^2 + AH^2 = OA^2$$ $$OH^2 + \left(\frac{l}{2}\right)^2 = R^2$$ $$OH = \sqrt{R^2 – \frac{l^2}{4}}$$
Chiều cao: $$h = R – OH = R – \sqrt{R^2 – \frac{l^2}{4}}$$
3. Ví dụ minh họa
Ví dụ 1: Viên phân có bán kính $R = 10$ cm và góc ở tâm $\alpha = 60°$. Tính chiều cao.
Lời giải:
Bước 1: Tính $\cos 30°$ (vì $\frac{\alpha}{2} = 30°$) $$\cos 30° = \frac{\sqrt{3}}{2}$$
Bước 2: Áp dụng công thức $$h = R\left(1 – \cos\frac{\alpha}{2}\right)$$ $$= 10\left(1 – \frac{\sqrt{3}}{2}\right)$$ $$= 10 – 5\sqrt{3}$$
Bước 3: Tính giá trị $$h \approx 10 – 8.66 = \boxed{1.34 \text{ cm}}$$
Ví dụ 2: Đường tròn có bán kính $R = 13$ cm, dây cung dài $l = 24$ cm. Tính chiều cao viên phân tương ứng.
Lời giải:
Áp dụng công thức: $$h = R – \sqrt{R^2 – \frac{l^2}{4}}$$ $$= 13 – \sqrt{169 – \frac{576}{4}}$$ $$= 13 – \sqrt{169 – 144}$$ $$= 13 – \sqrt{25}$$ $$= 13 – 5$$ $$= \boxed{8 \text{ cm}}$$
Kiểm tra: Với $R = 13$ cm và $h = 8$ cm, ta có thể tính lại $l$ để verify: $$l = 2\sqrt{2Rh – h^2} = 2\sqrt{208 – 64} = 2\sqrt{144} = 24$$ cm ✓
4. Mối quan hệ giữa $h$, $R$, $l$
Từ công thức $h = R – \sqrt{R^2 – \frac{l^2}{4}}$, ta có thể biến đổi:
$$R – h = \sqrt{R^2 – \frac{l^2}{4}}$$
Bình phương hai vế: $$(R – h)^2 = R^2 – \frac{l^2}{4}$$ $$R^2 – 2Rh + h^2 = R^2 – \frac{l^2}{4}$$ $$h^2 – 2Rh = -\frac{l^2}{4}$$ $$2Rh – h^2 = \frac{l^2}{4}$$
CÔNG THỨC QUAN HỆ:
$$\boxed{h(2R – h) = \frac{l^2}{4}}$$
Hoặc:
$$\boxed{l = 2\sqrt{h(2R – h)}}$$
Ứng dụng: Từ công thức này, biết 2 trong 3 đại lượng $h$, $R$, $l$ ta có thể tính đại lượng còn lại.
IV. CÔNG THỨC CHU VI VIÊN PHÂN
1. Định nghĩa chu vi
Chu vi viên phân là tổng độ dài của đường bao quanh hình viên phân, bao gồm:
- Độ dài cung tròn $\widehat{AB}$
- Độ dài dây cung $AB$
Lưu ý: Khác với chu vi hình tròn (chỉ có đường cong), chu vi viên phân có cả phần cong và phần thẳng.
2. Công thức tính chu vi
CÔNG THỨC TỔNG QUÁT:
$$\boxed{P = l_{\text{cung}} + l_{\text{dây}}}$$
Trong đó:
Độ dài cung tròn: $$l_{\text{cung}} = R\alpha$$ (với $\alpha$ tính bằng radian)
Hoặc khi $\alpha$ tính bằng độ: $$l_{\text{cung}} = \frac{2\pi R \alpha_{\text{(độ)}}}{360}$$
Độ dài dây cung:
Từ tam giác cân $OAB$, ta có: $$l_{\text{dây}} = 2R\sin\frac{\alpha}{2}$$
CÔNG THỨC ĐẦY ĐỦ:
$$\boxed{P = R\alpha + 2R\sin\frac{\alpha}{2}}$$
Hoặc viết gọn:
$$\boxed{P = R\left(\alpha + 2\sin\frac{\alpha}{2}\right)}$$
Điều kiện: $\alpha$ tính bằng radian
3. Ví dụ minh họa
Ví dụ 1: Viên phân có bán kính $R = 10$ cm và góc ở tâm $\alpha = 90°$. Tính chu vi.
Lời giải:
Bước 1: Chuyển đổi góc $$\alpha = 90° = \frac{\pi}{2} \text{ rad}$$
Bước 2: Tính các thành phần
Độ dài cung: $$l_{\text{cung}} = 10 \times \frac{\pi}{2} = 5\pi \text{ cm}$$
Độ dài dây cung (với $\frac{\alpha}{2} = 45°$): $$l_{\text{dây}} = 2 \times 10 \times \sin 45° = 20 \times \frac{\sqrt{2}}{2} = 10\sqrt{2} \text{ cm}$$
Bước 3: Tính chu vi $$P = 5\pi + 10\sqrt{2}$$ $$P \approx 15.71 + 14.14$$ $$P \approx \boxed{29.85 \text{ cm}}$$
Ví dụ 2: Viên phân có $R = 6$ cm, $\alpha = 60°$. Tính chu vi.
Lời giải:
Chuyển đổi: $\alpha = 60° = \frac{\pi}{3}$ rad
Độ dài cung: $$l_{\text{cung}} = 6 \times \frac{\pi}{3} = 2\pi \text{ cm}$$
Độ dài dây ($\sin 30° = 0.5$): $$l_{\text{dây}} = 2 \times 6 \times \sin 30° = 12 \times 0.5 = 6 \text{ cm}$$
Chu vi: $$P = 2\pi + 6 \approx 6.28 + 6 = \boxed{12.28 \text{ cm}}$$
V. CÁC TRƯỜNG HỢP ĐẶC BIỆT
1. Nửa hình tròn (Góc 180°)
Khi góc ở tâm $\alpha = 180° = \pi$ rad, dây cung $AB$ chính là đường kính và viên phân trở thành nửa hình tròn.
Diện tích: $$S = \frac{R^2}{2}(\pi – \sin\pi) = \frac{R^2}{2}(\pi – 0) = \frac{\pi R^2}{2}$$
$$\boxed{S_{\text{nửa HT}} = \frac{\pi R^2}{2}}$$
Chu vi: $$P = R\pi + 2R = R(\pi + 2)$$
$$\boxed{P_{\text{nửa HT}} = R(\pi + 2)}$$
Chiều cao: $$h = R(1 – \cos 90°) = R(1 – 0) = R$$
Chiều cao bằng bán kính (từ đường kính lên đỉnh)
2. Viên phân góc 60°
Góc $\alpha = 60° = \frac{\pi}{3}$ rad
Diện tích: $$S = \frac{R^2}{2}\left(\frac{\pi}{3} – \sin 60°\right)$$ $$= \frac{R^2}{2}\left(\frac{\pi}{3} – \frac{\sqrt{3}}{2}\right)$$ $$= R^2\left(\frac{\pi}{6} – \frac{\sqrt{3}}{4}\right)$$
$$\boxed{S_{60°} = R^2\left(\frac{\pi}{6} – \frac{\sqrt{3}}{4}\right) \approx 0.0908R^2}$$
Chiều cao: $$h = R(1 – \cos 30°) = R\left(1 – \frac{\sqrt{3}}{2}\right)$$
Dây cung: $$l = 2R\sin 30° = 2R \times 0.5 = R$$
Dây cung bằng bán kính (tam giác $OAB$ đều)
3. Viên phân góc 90°
Góc $\alpha = 90° = \frac{\pi}{2}$ rad
Diện tích: $$S = \frac{R^2}{2}\left(\frac{\pi}{2} – \sin 90°\right)$$ $$= \frac{R^2}{2}\left(\frac{\pi}{2} – 1\right)$$ $$= R^2\left(\frac{\pi}{4} – \frac{1}{2}\right)$$
$$\boxed{S_{90°} = R^2\left(\frac{\pi}{4} – \frac{1}{2}\right) \approx 0.2854R^2}$$
Chiều cao: $$h = R(1 – \cos 45°) = R\left(1 – \frac{\sqrt{2}}{2}\right)$$
Dây cung: $$l = 2R\sin 45° = 2R \times \frac{\sqrt{2}}{2} = R\sqrt{2}$$
4. Viên phân góc 120°
Góc $\alpha = 120° = \frac{2\pi}{3}$ rad
Diện tích: $$S = \frac{R^2}{2}\left(\frac{2\pi}{3} – \sin 120°\right)$$ $$= \frac{R^2}{2}\left(\frac{2\pi}{3} – \frac{\sqrt{3}}{2}\right)$$ $$= R^2\left(\frac{\pi}{3} – \frac{\sqrt{3}}{4}\right)$$
$$\boxed{S_{120°} = R^2\left(\frac{\pi}{3} – \frac{\sqrt{3}}{4}\right) \approx 0.6145R^2}$$
Chiều cao: $$h = R(1 – \cos 60°) = R\left(1 – \frac{1}{2}\right) = \frac{R}{2}$$
Dây cung: $$l = 2R\sin 60° = 2R \times \frac{\sqrt{3}}{2} = R\sqrt{3}$$
5. Bảng các giá trị thường gặp
| Góc ở tâm | Radian | Diện tích | Hệ số | Dây cung |
|---|---|---|---|---|
| 60° | $\frac{\pi}{3}$ | $R^2\left(\frac{\pi}{6} – \frac{\sqrt{3}}{4}\right)$ | $\approx 0.0908R^2$ | $R$ |
| 90° | $\frac{\pi}{2}$ | $R^2\left(\frac{\pi}{4} – \frac{1}{2}\right)$ | $\approx 0.2854R^2$ | $R\sqrt{2}$ |
| 120° | $\frac{2\pi}{3}$ | $R^2\left(\frac{\pi}{3} – \frac{\sqrt{3}}{4}\right)$ | $\approx 0.6145R^2$ | $R\sqrt{3}$ |
| 180° | $\pi$ | $\frac{\pi R^2}{2}$ | $\approx 1.5708R^2$ | $2R$ |
Cách sử dụng bảng: Nếu biết $R$ và góc, nhân $R^2$ với hệ số tương ứng để được diện tích.
VI. BẢNG TỔNG HỢP CÔNG THỨC ⭐
Bảng 1: Công thức chính (Quan trọng nhất)
| Đại lượng | Công thức | Đơn vị góc | Ghi chú |
|---|---|---|---|
| DIỆN TÍCH | $\boxed{S = \frac{R^2}{2}(\alpha – \sin\alpha)}$ | Radian | ⭐ Quan trọng nhất |
| Diện tích (độ) | $S = \frac{\pi R^2\alpha}{360} – \frac{R^2\sin\alpha}{2}$ | Độ | Dùng khi góc cho bằng độ |
| Chiều cao | $h = R(1 – \cos\frac{\alpha}{2})$ | Radian/Độ | Khoảng cách cung-dây |
| Chiều cao (dây) | $h = R – \sqrt{R^2 – \frac{l^2}{4}}$ | – | Khi biết dây cung |
| Chu vi | $P = R(\alpha + 2\sin\frac{\alpha}{2})$ | Radian | Cung + dây |
| Độ dài dây | $l = 2R\sin\frac{\alpha}{2}$ | Radian/Độ | Dây cung |
| Độ dài cung | $l_c = R\alpha$ | Radian | Cung tròn |
Bảng 2: Mối quan hệ các đại lượng
| Cho trước | Có thể tính | Công thức sử dụng |
|---|---|---|
| $R, \alpha$ | $S, h, P, l$ | Áp dụng trực tiếp các công thức cơ bản |
| $R, h$ | $\alpha, S, P, l$ | $\alpha = 2\arccos\frac{R-h}{R}$ |
| $R, l$ | $\alpha, S, h, P$ | $\alpha = 2\arcsin\frac{l}{2R}$ |
| $h, l$ | $R, \alpha, S, P$ | $R = \frac{h^2 + \frac{l^2}{4}}{2h}$ |
Bảng 3: Công thức bổ sung
| Công thức | Ý nghĩa |
|---|---|
| $h(2R – h) = \frac{l^2}{4}$ | Quan hệ $h$, $R$, $l$ |
| $S_{\text{quạt}} = \frac{R^2\alpha}{2}$ | Diện tích hình quạt |
| $S_{\triangle} = \frac{R^2\sin\alpha}{2}$ | Diện tích tam giác OAB |
| $l_c = \frac{2\pi R\alpha}{360}$ | Độ dài cung (góc độ) |
VII. PHƯƠNG PHÁP GIẢI BÀI TẬP
Phương pháp 1: Biết $R$ và góc $\alpha$
Đây là dạng cơ bản và hay gặp nhất.
Quy trình 4 bước:
Bước 1: Kiểm tra đơn vị góc
- Góc cho bằng độ (°) hay radian (rad)?
Bước 2: Chuyển đổi (nếu cần)
- Nếu góc bằng độ: $\alpha_{\text{(rad)}} = \alpha_{\text{(độ)}} \times \frac{\pi}{180}$
Bước 3: Áp dụng công thức $$S = \frac{R^2}{2}(\alpha – \sin\alpha)$$
Bước 4: Tính toán và kết luận
- Tính giá trị số
- Ghi đơn vị (cm², m²,…)
Phương pháp 2: Biết $R$ và chiều cao $h$
Khi đề bài cho bán kính và chiều cao.
Quy trình:
Bước 1: Tính góc từ chiều cao $$\cos\frac{\alpha}{2} = \frac{R – h}{R}$$ $$\frac{\alpha}{2} = \arccos\frac{R – h}{R}$$ $$\alpha = 2\arccos\frac{R – h}{R}$$
Bước 2: Tính diện tích
Thay $\alpha$ vào công thức: $$S = \frac{R^2}{2}(\alpha – \sin\alpha)$$
HOẶC dùng công thức trực tiếp: $$S = R^2\arccos\frac{R-h}{R} – (R-h)\sqrt{2Rh – h^2}$$
Phương pháp 3: Biết $R$ và dây cung $l$
Khi đề bài cho bán kính và độ dài dây cung.
Quy trình:
Bước 1: Tính góc từ dây cung $$\sin\frac{\alpha}{2} = \frac{l}{2R}$$ $$\frac{\alpha}{2} = \arcsin\frac{l}{2R}$$ $$\alpha = 2\arcsin\frac{l}{2R}$$
Bước 2: Tính diện tích
Thay $\alpha$ vào công thức diện tích.
Kiểm tra: Phải có $l \leq 2R$ (dây cung không dài hơn đường kính)
VIII. BÀI TẬP MẪU
Bài tập 1: Dạng cơ bản – Biết R và góc
Đề bài: Hình viên phân có bán kính $R = 12$ cm và góc ở tâm $\alpha = 60°$. Tính: a) Diện tích viên phân b) Chu vi viên phân c) Chiều cao viên phân
Lời giải:
Câu a) Diện tích:
Bước 1: Chuyển đổi góc $$\alpha = 60° = \frac{\pi}{3} \text{ rad}$$
Bước 2: Tính $\sin 60°$ $$\sin 60° = \frac{\sqrt{3}}{2} \approx 0.866$$
Bước 3: Áp dụng công thức $$S = \frac{R^2}{2}(\alpha – \sin\alpha)$$ $$= \frac{144}{2}\left(\frac{\pi}{3} – \frac{\sqrt{3}}{2}\right)$$ $$= 72\left(1.047 – 0.866\right)$$ $$= 72 \times 0.181$$ $$\approx \boxed{13.03 \text{ cm}^2}$$
Câu b) Chu vi:
Độ dài cung: $$l_c = R\alpha = 12 \times \frac{\pi}{3} = 4\pi \approx 12.57 \text{ cm}$$
Độ dài dây ($\sin 30° = 0.5$): $$l_d = 2 \times 12 \times \sin 30° = 24 \times 0.5 = 12 \text{ cm}$$
Chu vi: $$P = 12.57 + 12 = \boxed{24.57 \text{ cm}}$$
Câu c) Chiều cao:
$$h = R(1 – \cos\frac{\alpha}{2})$$ $$= 12(1 – \cos 30°)$$ $$= 12\left(1 – \frac{\sqrt{3}}{2}\right)$$ $$= 12(1 – 0.866)$$ $$= 12 \times 0.134$$ $$= \boxed{1.61 \text{ cm}}$$
Bài tập 2: Biết R và dây cung
Đề bài: Đường tròn có bán kính $R = 10$ cm, dây cung $AB = 16$ cm. Tính diện tích viên phân ứng với dây cung AB.
Lời giải:
Bước 1: Tính $\sin\frac{\alpha}{2}$ $$\sin\frac{\alpha}{2} = \frac{l}{2R} = \frac{16}{20} = 0.8$$
Bước 2: Tính $\frac{\alpha}{2}$ $$\frac{\alpha}{2} = \arcsin(0.8) \approx 53.13°$$
Bước 3: Tính $\alpha$ $$\alpha \approx 106.26° \approx 1.855 \text{ rad}$$
Bước 4: Tính $\sin\alpha$ $$\sin(106.26°) \approx 0.96$$
Bước 5: Tính diện tích $$S = \frac{100}{2}(1.855 – 0.96)$$ $$= 50 \times 0.895$$ $$\approx \boxed{44.75 \text{ cm}^2}$$
Bài tập 3: Biết R và chiều cao
Đề bài: Viên phân có bán kính $R = 15$ cm và chiều cao $h = 5$ cm. Tính diện tích.
Lời giải:
Bước 1: Tính $\cos\frac{\alpha}{2}$ $$\cos\frac{\alpha}{2} = \frac{R – h}{R} = \frac{15 – 5}{15} = \frac{10}{15} = \frac{2}{3} \approx 0.667$$
Bước 2: Tính $\frac{\alpha}{2}$ $$\frac{\alpha}{2} = \arccos(0.667) \approx 48.19°$$
Bước 3: Tính $\alpha$ $$\alpha \approx 96.38° \approx 1.682 \text{ rad}$$
Bước 4: Tính $\sin\alpha$ $$\sin(96.38°) \approx 0.993$$
Bước 5: Tính diện tích $$S = \frac{225}{2}(1.682 – 0.993)$$ $$= 112.5 \times 0.689$$ $$\approx \boxed{77.5 \text{ cm}^2}$$
Bài tập 4: Bài toán thực tế – Cửa sổ
Đề bài: Một cửa sổ có dạng hình viên phân với đường kính dây cung là 2 mét và chiều cao 0.3 mét. Tính diện tích kính cần dùng.
Lời giải:
Bước 1: Xác định dữ kiện
- Dây cung $l = 2$ m
- Chiều cao $h = 0.3$ m
Bước 2: Tính bán kính từ công thức $$h(2R – h) = \frac{l^2}{4}$$ $$0.3(2R – 0.3) = \frac{4}{4} = 1$$ $$0.6R – 0.09 = 1$$ $$R = \frac{1.09}{0.6} \approx 1.817 \text{ m}$$
Bước 3: Tính góc $$\sin\frac{\alpha}{2} = \frac{l}{2R} = \frac{2}{2 \times 1.817} = \frac{1}{1.817} \approx 0.55$$ $$\alpha \approx 2 \times 33.37° \approx 66.74° \approx 1.165 \text{ rad}$$
Bước 4: Tính diện tích $$S = \frac{R^2}{2}(\alpha – \sin\alpha)$$ $$\approx \frac{3.301}{2}(1.165 – 0.92)$$ $$\approx 1.65 \times 0.245$$ $$\approx \boxed{0.40 \text{ m}^2}$$
IX. KẾT LUẬN
Công thức QUAN TRỌNG NHẤT ⭐
Trong tất cả các công thức về hình viên phân, có 3 công thức cốt lõi cần nhớ:
1. DIỆN TÍCH (Quan trọng nhất!): $$\boxed{S = \frac{R^2}{2}(\alpha – \sin\alpha)}$$
2. CHIỀU CAO: $$\boxed{h = R\left(1 – \cos\frac{\alpha}{2}\right)}$$
3. CHU VI: $$\boxed{P = R\left(\alpha + 2\sin\frac{\alpha}{2}\right)}$$
Quy tắc vàng khi giải bài
Bước 1: Xác định góc $\alpha$
- Đơn vị radian hay độ? → Rất quan trọng!
- Nếu độ, chuyển sang radian: $\alpha_{\text{rad}} = \alpha_{\text{độ}} \times \frac{\pi}{180}$
Bước 2: Nhớ nguyên tắc
- Diện tích viên phân = Diện tích hình quạt – Diện tích tam giác
- $S_{\text{viên phân}} = S_{\text{quạt}} – S_{\triangle OAB}$
Bước 3: Chuyển đổi cẩn thận
- Góc độ → Radian khi tính diện tích
- Nhưng vẫn dùng độ khi tính $\sin\alpha$, $\cos\alpha$
Bước 4: Kiểm tra điều kiện
- $0 < \alpha < 2\pi$ (radian)
- $0° < \alpha < 360°$ (độ)
- Dây cung: $l \leq 2R$
Các chủ đề liên quan:
- Hình quạt tròn
- Diện tích hình tròn
- Độ dài cung tròn
- Góc ở tâm và góc nội tiếp
- Dây cung và tiếp tuyến

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
