Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ LỰC HƯỚNG TÂM
- 1. Lực hướng tâm là gì?
- 2. Đặc điểm quan trọng
- II. CÔNG THỨC GIA TỐC HƯỚNG TÂM
- 1. Gia tốc hướng tâm
- 2. Mối liên hệ giữa v và ω
- 3. Công thức với chu kỳ và tần số
- 4. Ví dụ minh họa
- III. CÔNG THỨC LỰC HƯỚNG TÂM
- 1. Công thức cơ bản
- 2. Các dạng công thức lực hướng tâm
- 3. Đặc điểm của lực hướng tâm
- 4. Ví dụ minh họa
- IV. CÁC TRƯỜNG HỢP ÁP DỤNG
- 1. Vật nối dây quay trong mặt phẳng ngang
- 2. Vật chuyển động trên đường tròn nằm ngang (Xe qua cua)
- 3. Chuyển động tròn đứng (Con lắc dây)
- 4. Vệ tinh quay quanh Trái Đất
- 5. Máy giặt vắt khô
- V. CHUYỂN ĐỘNG TRÒN BIẾN ĐỔI
- 1. Gia tốc tiếp tuyến
- 2. Gia tốc toàn phần
- 3. Lực toàn phần
- VI. BẢNG CÔNG THỨC TÓM TẮT
- A. Gia tốc hướng tâm
- B. Lực hướng tâm
- C. Các trường hợp đặc biệt
- D. Điều kiện quan trọng
- VII. BÀI TẬP MẪU
- Bài 1: Tính lực hướng tâm cơ bản
- VIII. PHƯƠNG PHÁP GIẢI NHANH
- 1. Các bước giải bài toán lực hướng tâm
- 2. Mẹo nhớ công thức
- IX. MẸO VÀ LƯU Ý
- 1. Các sai lầm thường gặp
- 2. Lưu ý quan trọng
- 3. Công thức hay dùng nhất
- X. KẾT LUẬN
- Công thức quan trọng nhất
- Lời khuyên cuối
I. GIỚI THIỆU VỀ LỰC HƯỚNG TÂM
1. Lực hướng tâm là gì?
Định nghĩa: Lực hướng tâm là lực (hoặc hợp lực) tác dụng lên vật chuyển động tròn, gây ra gia tốc hướng tâm và giữ cho vật chuyển động theo quỹ đạo tròn.
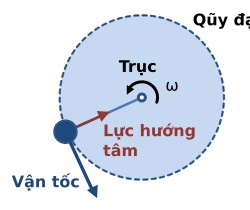
Ký hiệu:
- $\vec{F}_{ht}$ (lực hướng tâm)
- $\vec{F}_n$ (lực pháp tuyến)
Đặc điểm về hướng:
- Lực hướng tâm luôn hướng vào tâm của quỹ đạo tròn
- Vuông góc với vectơ vận tốc tại mọi điểm: $\vec{F}_{ht} \perp \vec{v}$
- Nằm trên bán kính quỹ đạo, hướng từ vật về tâm
Tác dụng:
- Làm thay đổi hướng của vectơ vận tốc
- Giữ cho vật chuyển động theo quỹ đạo tròn
- Trong chuyển động tròn đều: không làm thay đổi độ lớn vận tốc
2. Đặc điểm quan trọng
⚠️ LƯU Ý CỰC KỲ QUAN TRỌNG:
Lực hướng tâm KHÔNG PHẢI là một loại lực riêng biệt!
Lực hướng tâm là tên gọi chung cho các lực (hoặc hợp lực các lực) có tác dụng giữ vật chuyển động theo quỹ đạo tròn. Tùy vào từng trường hợp cụ thể, lực hướng tâm có thể là:
Các lực có thể đóng vai trò lực hướng tâm:
- Lực căng dây ($T$): Khi vật được buộc vào dây và quay tròn
- Lực ma sát ($F_{ms}$): Khi xe ô tô qua đường cong
- Lực hấp dẫn ($F_{hd}$): Khi vệ tinh quay quanh Trái Đất
- Lực đàn hồi ($F_{đh}$): Khi lò xo nối với vật quay tròn
- Thành phần của trọng lực: Trong một số trường hợp chuyển động trên mặt cầu
- Lực nén của thành bình: Trong máy giặt vắt khô
- Hợp lực của nhiều lực: Trong các trường hợp phức tạp
II. CÔNG THỨC GIA TỐC HƯỚNG TÂM
1. Gia tốc hướng tâm
Định nghĩa: Gia tốc hướng tâm là gia tốc của vật trong chuyển động tròn, luôn hướng vào tâm quỹ đạo.
Công thức cơ bản:
$$\boxed{a_{ht} = \frac{v^2}{r} = \omega^2 r}$$
Trong đó:
- $a_{ht}$: Gia tốc hướng tâm (m/s²)
- $v$: Vận tốc dài (vận tốc tuyến tính) (m/s)
- $r$: Bán kính quỹ đạo tròn (m)
- $\omega$: Vận tốc góc (rad/s)
Hướng của gia tốc hướng tâm:
- Luôn luôn hướng vào tâm của quỹ đạo tròn
- Vuông góc với vectơ vận tốc: $\vec{a}_{ht} \perp \vec{v}$
- Độ lớn không đổi trong chuyển động tròn đều
Ý nghĩa:
- Gia tốc hướng tâm đặc trưng cho sự thay đổi hướng của vận tốc
- Càng lớn khi vật chuyển động nhanh (v lớn) hoặc quỹ đạo cong nhiều (r nhỏ)
2. Mối liên hệ giữa v và ω
Công thức liên hệ:
$$\boxed{v = \omega r}$$
Suy ra: $$\omega = \frac{v}{r}$$
Thay vào công thức gia tốc, ta có các dạng:
$$a_{ht} = \frac{v^2}{r} = \omega^2 r = v\omega$$
Chú ý:
- Khi biết hai trong ba đại lượng $v$, $\omega$, $r$ thì có thể tính đại lượng còn lại
- Công thức $v = \omega r$ là cầu nối giữa các đại lượng
3. Công thức với chu kỳ và tần số
Chu kỳ T (chu kì):
Thời gian để vật quay được một vòng tròn:
$$\boxed{T = \frac{2\pi r}{v} = \frac{2\pi}{\omega}}$$
Đơn vị: giây (s)
Tần số f:
Số vòng quay được trong một giây:
$$\boxed{f = \frac{1}{T}}$$
Đơn vị: vòng/giây hay Hz (hertz)
Mối liên hệ: $$\omega = 2\pi f = \frac{2\pi}{T}$$
$$v = \frac{2\pi r}{T} = 2\pi rf$$
Gia tốc hướng tâm theo T và f:
$$\boxed{a_{ht} = \frac{4\pi^2 r}{T^2} = 4\pi^2 f^2 r}$$
4. Ví dụ minh họa
Ví dụ 1: Một vật chuyển động tròn đều trên quỹ đạo có bán kính $r = 2$ m với vận tốc $v = 4$ m/s. Tính gia tốc hướng tâm.
Lời giải:
Áp dụng công thức: $$a_{ht} = \frac{v^2}{r} = \frac{4^2}{2} = \frac{16}{2} = 8 \text{ m/s}^2$$
Đáp án: Gia tốc hướng tâm là 8 m/s².
III. CÔNG THỨC LỰC HƯỚNG TÂM
1. Công thức cơ bản
Từ định luật II Newton:
Theo định luật II Newton: $\vec{F} = m\vec{a}$
Áp dụng cho chuyển động tròn:
$$\boxed{\vec{F}{ht} = m\vec{a}{ht}}$$
Độ lớn của lực hướng tâm:
$$\boxed{F_{ht} = m \cdot a_{ht} = m\frac{v^2}{r} = m\omega^2 r}$$
Trong đó:
- $F_{ht}$: Độ lớn lực hướng tâm (N – Newton)
- $m$: Khối lượng của vật (kg)
- $v$: Vận tốc dài (m/s)
- $r$: Bán kính quỹ đạo (m)
- $\omega$: Vận tốc góc (rad/s)
Hướng: Luôn hướng vào tâm quỹ đạo tròn
2. Các dạng công thức lực hướng tâm
Dạng 1: Theo vận tốc dài $$\boxed{F_{ht} = m\frac{v^2}{r}}$$
Sử dụng khi: Biết khối lượng, vận tốc dài và bán kính
Dạng 2: Theo vận tốc góc $$\boxed{F_{ht} = m\omega^2 r}$$
Sử dụng khi: Biết khối lượng, vận tốc góc và bán kính
Dạng 3: Theo chu kỳ $$\boxed{F_{ht} = m\frac{4\pi^2 r}{T^2}}$$
Sử dụng khi: Biết khối lượng, bán kính và chu kỳ
Dạng 4: Theo tần số $$\boxed{F_{ht} = 4\pi^2 mf^2 r}$$
Sử dụng khi: Biết khối lượng, tần số và bán kính
3. Đặc điểm của lực hướng tâm
Về hướng:
- Luôn hướng vào tâm quỹ đạo tròn
- Nằm trên bán kính, hướng từ vật về tâm
Về quan hệ với vận tốc:
- Vuông góc với vectơ vận tốc: $\vec{F}_{ht} \perp \vec{v}$
- Do đó lực hướng tâm không sinh công: $A = F \cdot s \cdot \cos 90° = 0$
Về tác dụng:
- Chỉ làm thay đổi hướng của vận tốc
- Không làm thay đổi độ lớn của vận tốc (trong chuyển động tròn đều)
Về độ lớn:
- Tỷ lệ thuận với khối lượng: $m$ càng lớn → $F_{ht}$ càng lớn
- Tỷ lệ thuận với bình phương vận tốc: $v$ càng lớn → $F_{ht}$ tăng rất nhanh
- Tỷ lệ nghịch với bán kính: $r$ càng nhỏ (cua gấp) → $F_{ht}$ càng lớn
4. Ví dụ minh họa
Ví dụ 2: Một vật có khối lượng $m = 0.5$ kg chuyển động tròn đều trên quỹ đạo bán kính $r = 1$ m với vận tốc $v = 6$ m/s. Tính lực hướng tâm tác dụng lên vật.
Lời giải:
Áp dụng công thức: $$F_{ht} = m\frac{v^2}{r} = 0.5 \times \frac{6^2}{1} = 0.5 \times \frac{36}{1} = 0.5 \times 36 = 18 \text{ N}$$
Đáp án: Lực hướng tâm là 18 N.
IV. CÁC TRƯỜNG HỢP ÁP DỤNG
1. Vật nối dây quay trong mặt phẳng ngang
Tình huống: Vật được gắn vào đầu một sợi dây, quay tròn đều trong mặt phẳng nằm ngang.
Phân tích:
- Lực căng dây $T$ hướng vào tâm
- Lực căng dây đóng vai trò lực hướng tâm
Công thức: $$\boxed{F_{ht} = T = m\frac{v^2}{r}}$$
Ví dụ 3: Một vật khối lượng $m = 0.2$ kg được buộc vào sợi dây dài $l = 0.5$ m, quay tròn đều trong mặt phẳng ngang với vận tốc $v = 2$ m/s. Tính lực căng dây.
Lời giải: $$T = m\frac{v^2}{r} = 0.2 \times \frac{2^2}{0.5} = 0.2 \times \frac{4}{0.5} = 0.2 \times 8 = 1.6 \text{ N}$$
Đáp án: Lực căng dây là 1.6 N.
2. Vật chuyển động trên đường tròn nằm ngang (Xe qua cua)
Tình huống: Xe ô tô chuyển động qua đoạn đường cong (đường tròn) bán kính $r$ trên mặt đường nằm ngang.
Phân tích:
- Lực ma sát nghỉ giữa bánh xe và mặt đường hướng vào tâm
- Lực ma sát này đóng vai trò lực hướng tâm
Công thức lực hướng tâm: $$\boxed{F_{ht} = F_{ms} = m\frac{v^2}{r}}$$
Điều kiện để xe không trượt:
Lực ma sát cần thiết phải không vượt quá lực ma sát nghỉ cực đại: $$m\frac{v^2}{r} \leq \mu mg$$
Rút gọn: $$v^2 \leq \mu gr$$
$$\boxed{v \leq \sqrt{\mu gr}}$$
Vận tốc tối đa để xe không trượt: $$\boxed{v_{max} = \sqrt{\mu gr}}$$
Trong đó:
- $\mu$: Hệ số ma sát giữa bánh xe và mặt đường
- $g$: Gia tốc trọng trường ($g \approx 10$ m/s²)
Ví dụ 4: Xe ô tô qua đoạn cua có bán kính $r = 50$ m. Hệ số ma sát giữa bánh xe và mặt đường là $\mu = 0.8$. Tính vận tốc tối đa để xe không bị trượt.
Lời giải: $$v_{max} = \sqrt{\mu gr} = \sqrt{0.8 \times 10 \times 50} = \sqrt{400} = 20 \text{ m/s}$$
Đổi ra km/h: $v_{max} = 20 \times 3.6 = 72$ km/h
Đáp án: Vận tốc tối đa là 20 m/s hay 72 km/h.
3. Chuyển động tròn đứng (Con lắc dây)
Tình huống: Vật được treo vào dây, quay tròn trong mặt phẳng thẳng đứng.
a) Tại điểm thấp nhất:
Phân tích lực:
- Lực căng dây $T$ hướng lên (vào tâm)
- Trọng lực $P = mg$ hướng xuống (ra khỏi tâm)
Phương trình lực hướng tâm: $$F_{ht} = T – P = m\frac{v^2}{r}$$
$$\boxed{T = mg + m\frac{v^2}{r}}$$
Nhận xét:
- Lực căng dây tại điểm thấp nhất là lớn nhất: $T_{max}$
- $T > P$ luôn đúng tại điểm thấp nhất
b) Tại điểm cao nhất:
Phân tích lực:
- Cả lực căng dây $T$ và trọng lực $P$ đều hướng xuống (vào tâm)
Phương trình lực hướng tâm: $$F_{ht} = T + P = m\frac{v^2}{r}$$
$$\boxed{T = m\frac{v^2}{r} – mg}$$
Điều kiện dây không chùng:
Để dây không bị chùng, lực căng phải không âm: $$T \geq 0$$
$$m\frac{v^2}{r} – mg \geq 0$$
$$m\frac{v^2}{r} \geq mg$$
$$v^2 \geq gr$$
$$\boxed{v \geq \sqrt{gr}}$$
Vận tốc tối thiểu tại điểm cao nhất: $$\boxed{v_{min} = \sqrt{gr}}$$
Nhận xét:
- Lực căng dây tại điểm cao nhất là nhỏ nhất: $T_{min}$
- Trong trường hợp giới hạn: $T = 0$, vật chỉ còn trọng lực đóng vai trò lực hướng tâm
4. Vệ tinh quay quanh Trái Đất
Tình huống: Vệ tinh nhân tạo chuyển động tròn đều quanh Trái Đất.
Phân tích:
- Lực hấp dẫn giữa Trái Đất và vệ tinh đóng vai trò lực hướng tâm
Công thức:
Lực hướng tâm bằng lực hấp dẫn: $$F_{ht} = F_{hd}$$
$$m\frac{v^2}{r} = G\frac{Mm}{r^2}$$
Trong đó:
- $G$: Hằng số hấp dẫn ($G = 6.67 \times 10^{-11}$ N·m²/kg²)
- $M$: Khối lượng Trái Đất
- $m$: Khối lượng vệ tinh
- $r$: Khoảng cách từ tâm Trái Đất đến vệ tinh
Vận tốc của vệ tinh:
Rút gọn khối lượng vệ tinh: $$\frac{v^2}{r} = G\frac{M}{r^2}$$
$$\boxed{v = \sqrt{\frac{GM}{r}}}$$
Nhận xét:
- Vận tốc vệ tinh không phụ thuộc vào khối lượng của nó
- Vệ tinh càng gần Trái Đất (r nhỏ) thì vận tốc càng lớn
5. Máy giặt vắt khô
Tình huống: Quần áo ướt trong lồng giặt quay tròn với tốc độ cao.
Phân tích:
- Thành lồng giặt cung cấp lực hướng tâm cho quần áo
- Khi lực hướng tâm cần thiết lớn hơn lực mà thành lồng có thể cung cấp, nước sẽ văng ra ngoài qua các lỗ
Nguyên lý:
- Tốc độ quay càng lớn → lực hướng tâm cần thiết càng lớn
- Nước bị văng ra ngoài nhiều hơn → quần áo khô nhanh hơn
Công thức: $$F_{ht} = m\omega^2 r$$
Với $\omega$ lớn → $F_{ht}$ rất lớn → hiệu quả vắt tốt
V. CHUYỂN ĐỘNG TRÒN BIẾN ĐỔI
1. Gia tốc tiếp tuyến
Định nghĩa: Trong chuyển động tròn nhanh dần hoặc chậm dần, ngoài gia tốc hướng tâm còn có gia tốc tiếp tuyến.
Công thức: $$\boxed{a_t = \frac{dv}{dt}}$$
Hoặc trong trường hợp đơn giản: $$a_t = \frac{\Delta v}{\Delta t}$$
Hướng:
- Tiếp tuyến với quỹ đạo tại vị trí của vật
- Cùng chiều với $\vec{v}$ nếu chuyển động nhanh dần
- Ngược chiều với $\vec{v}$ nếu chuyển động chậm dần
2. Gia tốc toàn phần
Công thức vectơ: $$\boxed{\vec{a} = \vec{a}_{ht} + \vec{a}_t}$$
Chú ý quan trọng: $\vec{a}_{ht} \perp \vec{a}_t$ (vuông góc nhau)
Độ lớn gia tốc toàn phần:
Do hai gia tốc vuông góc nên áp dụng định lý Pythagore: $$\boxed{a = \sqrt{a_{ht}^2 + a_t^2}}$$
3. Lực toàn phần
Công thức: $$\boxed{F = ma = m\sqrt{a_{ht}^2 + a_t^2}}$$
Lưu ý:
- Lực hướng tâm vẫn được tính: $F_{ht} = ma_{ht} = m\frac{v^2}{r}$
- Lực tiếp tuyến: $F_t = ma_t$
- Hợp lực: $F = \sqrt{F_{ht}^2 + F_t^2}$
VI. BẢNG CÔNG THỨC TÓM TẮT
A. Gia tốc hướng tâm
| Công thức | Khi nào dùng |
|---|---|
| $a_{ht} = \frac{v^2}{r}$ | Biết vận tốc dài $v$ và bán kính $r$ |
| $a_{ht} = \omega^2 r$ | Biết vận tốc góc $\omega$ và bán kính $r$ |
| $a_{ht} = v\omega$ | Biết cả $v$ và $\omega$ |
| $a_{ht} = \frac{4\pi^2 r}{T^2}$ | Biết chu kỳ $T$ và bán kính $r$ |
| $a_{ht} = 4\pi^2 f^2 r$ | Biết tần số $f$ và bán kính $r$ |
B. Lực hướng tâm
| Công thức | Khi nào dùng |
|---|---|
| $F_{ht} = m\frac{v^2}{r}$ | Biết $m$, $v$, $r$ |
| $F_{ht} = m\omega^2 r$ | Biết $m$, $\omega$, $r$ |
| $F_{ht} = \frac{4\pi^2 mr}{T^2}$ | Biết $m$, $T$, $r$ |
| $F_{ht} = 4\pi^2 mf^2 r$ | Biết $m$, $f$, $r$ |
C. Các trường hợp đặc biệt
| Tình huống | Công thức lực hướng tâm |
|---|---|
| Dây quay ngang | $F_{ht} = T = m\frac{v^2}{r}$ |
| Xe qua cua | $F_{ht} = F_{ms} = m\frac{v^2}{r} \leq \mu mg$ |
| Điểm thấp nhất (dây quay đứng) | $T = mg + m\frac{v^2}{r}$ |
| Điểm cao nhất (dây quay đứng) | $T = m\frac{v^2}{r} – mg$ |
| Vệ tinh quay | $F_{ht} = F_{hd} = G\frac{Mm}{r^2}$ |
D. Điều kiện quan trọng
| Yêu cầu | Công thức điều kiện |
|---|---|
| Xe không trượt khi qua cua | $v \leq \sqrt{\mu gr}$ |
| Dây không chùng tại điểm cao nhất | $v \geq \sqrt{gr}$ |
| Vận tốc tối đa xe qua cua | $v_{max} = \sqrt{\mu gr}$ |
| Vận tốc tối thiểu tại đỉnh (quay đứng) | $v_{min} = \sqrt{gr}$ |
VII. BÀI TẬP MẪU
Bài 1: Tính lực hướng tâm cơ bản
Đề bài: Một vật có khối lượng $m = 1$ kg chuyển động tròn đều với bán kính $r = 2$ m và vận tốc $v = 4$ m/s. Tính lực hướng tâm tác dụng lên vật.
Lời giải:
Áp dụng công thức: $$F_{ht} = m\frac{v^2}{r} = 1 \times \frac{4^2}{2} = 1 \times \frac{16}{2} = 8 \text{ N}$$
Đáp án: $F_{ht} = 8$ N
Bài 2: Xe qua cua – tính vận tốc tối đa
Đề bài: Một xe ô tô chuyển động qua đoạn đường cong có bán kính $r = 100$ m. Hệ số ma sát giữa lốp xe và mặt đường là $\mu = 0.6$. Tính vận tốc tối đa để xe không bị trượt.
Lời giải:
Áp dụng công thức: $$v_{max} = \sqrt{\mu gr} = \sqrt{0.6 \times 10 \times 100} = \sqrt{600} \approx 24.5 \text{ m/s}$$
Đổi ra km/h: $$v_{max} = 24.5 \times 3.6 \approx 88 \text{ km/h}$$
Đáp án: $v_{max} \approx 24.5$ m/s $\approx 88$ km/h
Bài 3: Dây quay đứng – vận tốc tối thiểu
Đề bài: Một vật có khối lượng $m = 0.5$ kg được gắn vào đầu sợi dây dài $l = 1$ m, quay tròn trong mặt phẳng thẳng đứng. Tính vận tốc tối thiểu của vật tại điểm cao nhất để dây không bị chùng.
Lời giải:
Điều kiện dây không chùng tại điểm cao nhất: $$v_{min} = \sqrt{gr} = \sqrt{10 \times 1} = \sqrt{10} \approx 3.16 \text{ m/s}$$
Đáp án: $v_{min} = \sqrt{10} \approx 3.16$ m/s
Bài 4: Lực căng dây tại điểm thấp nhất
Đề bài: (Tiếp theo Bài 3) Nếu vật có vận tốc $v = 6$ m/s tại điểm thấp nhất của quỹ đạo, tính lực căng dây tại vị trí này.
Lời giải:
Tại điểm thấp nhất: $$T = mg + m\frac{v^2}{r}$$ $$T = 0.5 \times 10 + 0.5 \times \frac{6^2}{1}$$ $$T = 5 + 0.5 \times 36$$ $$T = 5 + 18 = 23 \text{ N}$$
Đáp án: $T = 23$ N
Bài 5: Tính chu kỳ từ lực hướng tâm
Đề bài: Một vật có khối lượng $m = 2$ kg chuyển động tròn đều với bán kính $r = 0.5$ m. Lực hướng tâm tác dụng lên vật là $F_{ht} = 40$ N. Tính chu kỳ quay của vật.
Lời giải:
Từ công thức: $$F_{ht} = \frac{4\pi^2 mr}{T^2}$$
Suy ra: $$T^2 = \frac{4\pi^2 mr}{F_{ht}} = \frac{4\pi^2 \times 2 \times 0.5}{40} = \frac{4\pi^2}{40} = \frac{\pi^2}{10}$$
$$T = \sqrt{\frac{\pi^2}{10}} = \frac{\pi}{\sqrt{10}} \approx \frac{3.14}{3.16} \approx 1 \text{ s}$$
Đáp án: $T \approx 1$ giây
VIII. PHƯƠNG PHÁP GIẢI NHANH
1. Các bước giải bài toán lực hướng tâm
Bước 1: Vẽ hình và xác định
- Vẽ quỹ đạo tròn và xác định tâm O
- Đánh dấu vị trí vật đang xét
- Vẽ bán kính từ tâm đến vật
Bước 2: Phân tích các lực
- Liệt kê tất cả các lực tác dụng lên vật
- Xác định hướng của từng lực
Bước 3: Chiếu lên phương hướng tâm
- Chọn chiều dương hướng vào tâm
- Chiếu các lực lên phương này
- Lực nào hướng vào tâm thì dương, ra khỏi tâm thì âm
Bước 4: Áp dụng công thức
- Tổng hợp lực theo phương hướng tâm = Lực hướng tâm
- Áp dụng: $F_{ht} = m\frac{v^2}{r}$
2. Mẹo nhớ công thức
“F bằng m nhân v bình chia r” $$F_{ht} = m\frac{v^2}{r}$$
“a bằng v bình chia r” $$a_{ht} = \frac{v^2}{r}$$
Điểm thấp nhất: T lớn nhất, CỘNG mg $$T_{max} = mg + m\frac{v^2}{r}$$
Điểm cao nhất: T nhỏ nhất, TRỪ mg $$T_{min} = m\frac{v^2}{r} – mg$$
Xe không trượt: v ≤ căn mu g r $$v_{max} = \sqrt{\mu gr}$$
Dây không chùng: v ≥ căn g r $$v_{min} = \sqrt{gr}$$
IX. MẸO VÀ LƯU Ý
1. Các sai lầm thường gặp
❌ SAI LẦM 1: Nghĩ rằng lực hướng tâm là một loại lực độc lập, riêng biệt
ĐÚNG: Lực hướng tâm là tên gọi chung cho lực (hoặc hợp lực) giữ vật chuyển động tròn
❌ SAI LẦM 2: Quên rằng lực hướng tâm luôn hướng vào tâm
ĐÚNG: Lực hướng tâm LUÔN LUÔN hướng vào tâm quỹ đạo, không bao giờ hướng ra ngoài
❌ SAI LẦM 3: Nhầm công thức tại điểm cao và điểm thấp
ĐÚNG:
- Điểm thấp: $T = mg + m\frac{v^2}{r}$ (CỘNG)
- Điểm cao: $T = m\frac{v^2}{r} – mg$ (TRỪ)
❌ SAI LẦM 4: Quên điều kiện $v_{min}$ tại điểm cao nhất
ĐÚNG: Để dây không chùng: $v \geq \sqrt{gr}$
2. Lưu ý quan trọng
✅ Lực hướng tâm KHÔNG phải lực độc lập mà là tên gọi chung cho các lực có tác dụng giữ vật chuyển động tròn
✅ Lực hướng tâm luôn vuông góc với vận tốc: $\vec{F}_{ht} \perp \vec{v}$
✅ Lực hướng tâm không sinh công vì luôn vuông góc với chuyển động: $A = F \cdot s \cdot \cos 90° = 0$
✅ Lực hướng tâm chỉ làm đổi hướng, không làm thay đổi độ lớn vận tốc (trong chuyển động tròn đều)
✅ Trong chuyển động tròn đều: $|\vec{v}|$ = const, nhưng $\vec{v}$ thay đổi về hướng
3. Công thức hay dùng nhất
Ba công thức vàng:
$$\boxed{F_{ht} = m\frac{v^2}{r}}$$
$$\boxed{v_{max} = \sqrt{\mu gr}}$$
$$\boxed{v_{min} = \sqrt{gr}}$$
X. KẾT LUẬN
Bài viết đã trình bày đầy đủ và chi tiết về lực hướng tâm:
Khái niệm cơ bản:
- Lực hướng tâm không phải lực riêng biệt
- Là tên gọi chung cho lực giữ vật chuyển động tròn
- Luôn hướng vào tâm, vuông góc với vận tốc
Công thức gia tốc hướng tâm: $$a_{ht} = \frac{v^2}{r} = \omega^2 r$$
Công thức lực hướng tâm: $$F_{ht} = m\frac{v^2}{r} = m\omega^2 r$$
Điều kiện xe không trượt: $$v_{max} = \sqrt{\mu gr}$$
Điều kiện dây không chùng (tại điểm cao nhất): $$v_{min} = \sqrt{gr}$$
Công thức tại điểm thấp nhất: $$T_{max} = mg + m\frac{v^2}{r}$$
Công thức tại điểm cao nhất: $$T_{min} = m\frac{v^2}{r} – mg$$
Công thức quan trọng nhất
$$\boxed{F_{ht} = m\frac{v^2}{r} = m\omega^2 r}$$
Đây là công thức nền tảng, cần phải nhớ vững để giải mọi bài toán về lực hướng tâm.
Lời khuyên cuối
Hiểu rõ bản chất: Lực hướng tâm không phải một loại lực riêng – đây là điều cực kỳ quan trọng!
Học thuộc công thức cơ bản: $F = m\frac{v^2}{r}$ là công thức vàng
Phân biệt rõ điểm cao và điểm thấp: Một CỘNG, một TRỪ – đừng nhầm lẫn!
Nhớ các điều kiện:
- Không trượt: $v \leq \sqrt{\mu gr}$
- Không chùng dây: $v \geq \sqrt{gr}$
Luyện tập nhiều: Làm nhiều bài tập để thành thạo các trường hợp khác nhau

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
