Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. Giới Thiệu
- 1. Khái niệm cơ bản
- 2. Đơn vị đo góc
- II. Công Thức Tính Độ Dài Cung Tròn
- 1. Công thức cơ bản
- 2. Bảng công thức tổng hợp
- 3. Ví dụ minh họa
- 4. Trường hợp đặc biệt
- III. Công Thức Tính Dây Cung
- 1. Định nghĩa
- 2. Công thức tính dây cung
- 3. Bảng giá trị dây cung đặc biệt
- 4. Ví dụ minh họa
- 5. So sánh độ dài cung và dây cung
- IV. Công Thức Tính Số Đo Cung
- 1. Công thức tính số đo cung (góc ở tâm)
- 2. Công thức tính từ dây cung
- 3. Ví dụ
- V. Công Thức Tính Diện Tích Hình Quạt Tròn
- 1. Khái niệm hình quạt tròn
- 2. Công thức cơ bản
- 3. Bảng công thức tổng hợp
- 4. Các trường hợp đặc biệt
- 5. Ví dụ minh họa
- VI. Công Thức Tính Chu Vi Hình Quạt Tròn
- Công thức
- Ví dụ
- VII. Công Thức Tính Diện Tích Cung Tròn (Hình Viên Phân)
- 1. Khái niệm hình viên phân
- 2. Công thức
- 3. Công thức tam giác trong hình quạt
- 4. Ví dụ minh họa
- VIII. Bảng Tổng Hợp Công Thức
- Bảng 1: Công thức về cung tròn
- Bảng 2: Công thức về hình quạt tròn
- Bảng 3: Giá trị đặc biệt
- IX. Bài Tập Vận Dụng
- Dạng 1: Bài tập về cung tròn
- Dạng 2: Bài tập về hình quạt tròn
- X. Kết Luận
- Tổng kết
- Mẹo nhớ
- Ứng dụng thực tế
I. Giới Thiệu
1. Khái niệm cơ bản
Cung tròn là phần đường tròn được giới hạn bởi hai điểm trên đường tròn đó. Khi nói đến cung tròn, ta thường quan tâm đến độ dài của nó.
Hình quạt tròn là phần hình tròn được giới hạn bởi hai bán kính và một cung tròn nối hai đầu mút của hai bán kính đó.
Phân biệt cung nhỏ và cung lớn:
- Cung nhỏ: Cung có độ dài ngắn hơn, ứng với góc ở tâm nhỏ hơn 180°
- Cung lớn: Cung có độ dài dài hơn, ứng với góc ở tâm lớn hơn 180°
- Khi góc ở tâm = 180°, hai cung bằng nhau (nửa đường tròn)
2. Đơn vị đo góc
Độ (degree):
- 1 vòng tròn = 360°
- 1 góc vuông = 90°
- Ký hiệu: °
Radian:
- 1 vòng tròn = 2π radian
- 1 radian ≈ 57.3°
- Ký hiệu: rad (hoặc không ghi)
Công thức chuyển đổi:
$$\alpha \text{ (độ)} = \alpha \times \frac{\pi}{180} \text{ (radian)}$$
$$\alpha \text{ (radian)} = \alpha \times \frac{180}{\pi} \text{ (độ)}$$
Ví dụ:
- 60° = $\frac{60\pi}{180} = \frac{\pi}{3}$ rad
- $\frac{\pi}{2}$ rad = $\frac{\pi}{2} \times \frac{180}{\pi} = 90°$
II. Công Thức Tính Độ Dài Cung Tròn
1. Công thức cơ bản
Cho đường tròn bán kính $R$, cung tròn có số đo góc ở tâm $\alpha$:
a) Góc tính bằng radian:
$$l = R \cdot \alpha$$
Trong đó:
- $l$: độ dài cung (đơn vị: cm, m, km…)
- $R$: bán kính đường tròn
- $\alpha$: số đo góc ở tâm (radian)
b) Góc tính bằng độ:
$$l = \frac{\pi R \alpha}{180}$$
Hoặc viết dưới dạng:
$$l = \frac{2\pi R \cdot \alpha}{360} = \frac{\pi R \alpha}{180}$$
Giải thích:
- Chu vi đường tròn là $2\pi R$
- Góc $\alpha$ chiếm $\frac{\alpha}{360}$ của cả vòng tròn
- Do đó độ dài cung = $2\pi R \times \frac{\alpha}{360}$
2. Bảng công thức tổng hợp
| Đại lượng cần tìm | Công thức (radian) | Công thức (độ) |
|---|---|---|
| Độ dài cung $l$ | $l = R\alpha$ | $l = \frac{\pi R\alpha}{180}$ |
| Bán kính $R$ | $R = \frac{l}{\alpha}$ | $R = \frac{180l}{\pi\alpha}$ |
| Góc ở tâm $\alpha$ | $\alpha = \frac{l}{R}$ | $\alpha = \frac{180l}{\pi R}$ |
3. Ví dụ minh họa
Ví dụ 1: Tính độ dài cung tròn có bán kính $R = 6$ cm, góc ở tâm $\alpha = 60°$
Lời giải:
Cách 1: Đổi góc sang radian
- $60° = \frac{60\pi}{180} = \frac{\pi}{3}$ rad
- Áp dụng công thức: $l = R\alpha = 6 \times \frac{\pi}{3} = 2\pi$ cm
Cách 2: Dùng công thức với góc độ
- $l = \frac{\pi R\alpha}{180} = \frac{\pi \times 6 \times 60}{180} = 2\pi$ cm
Đáp án: $l = 2\pi$ cm (≈ 6.28 cm)
Ví dụ 2: Cung tròn có độ dài $5\pi$ cm, bán kính 10 cm. Tính số đo góc ở tâm.
Lời giải:
$$\alpha = \frac{l}{R} = \frac{5\pi}{10} = \frac{\pi}{2} \text{ rad}$$
Đổi sang độ: $\alpha = \frac{\pi}{2} \times \frac{180}{\pi} = 90°$
Đáp án: $\alpha = \frac{\pi}{2}$ rad = 90°
Ví dụ 3: Độ dài cung là $12\pi$ cm, góc ở tâm là 120°. Tính bán kính.
Lời giải:
$$R = \frac{180l}{\pi\alpha} = \frac{180 \times 12\pi}{\pi \times 120} = \frac{2160}{120} = 18 \text{ cm}$$
Đáp án: $R = 18$ cm
4. Trường hợp đặc biệt
| Góc ở tâm | Độ dài cung |
|---|---|
| $\alpha = 360°$ (1 vòng) | $l = 2\pi R$ (chu vi) |
| $\alpha = 180°$ (nửa vòng) | $l = \pi R$ |
| $\alpha = 90°$ (1/4 vòng) | $l = \frac{\pi R}{2}$ |
| $\alpha = 60°$ | $l = \frac{\pi R}{3}$ |
| $\alpha = 45°$ | $l = \frac{\pi R}{4}$ |
| $\alpha = 30°$ | $l = \frac{\pi R}{6}$ |
III. Công Thức Tính Dây Cung
1. Định nghĩa
Dây cung là đoạn thẳng nối hai đầu mút của cung tròn.
Lưu ý quan trọng:
- Dây cung là đoạn thẳng
- Độ dài cung là độ dài đường cong
- Dây cung ≠ Độ dài cung
- Độ dài cung > Độ dài dây cung (với cùng góc ở tâm < 180°)
2. Công thức tính dây cung
Cho đường tròn bán kính $R$, góc ở tâm $\alpha$:
$$AB = 2R\sin\frac{\alpha}{2}$$
Trong đó:
- $AB$: độ dài dây cung
- $R$: bán kính đường tròn
- $\alpha$: góc ở tâm (có thể tính bằng radian hoặc độ)
Chứng minh:
Từ tam giác OAB cân tại O, kẻ đường cao OH. Ta có:
- $\widehat{AOH} = \frac{\alpha}{2}$
- $AH = R\sin\frac{\alpha}{2}$
- $AB = 2AH = 2R\sin\frac{\alpha}{2}$
3. Bảng giá trị dây cung đặc biệt
| Góc ở tâm $\alpha$ | Độ dài dây cung $AB$ |
|---|---|
| 60° | $AB = R$ |
| 90° | $AB = R\sqrt{2}$ |
| 120° | $AB = R\sqrt{3}$ |
| 180° | $AB = 2R$ (đường kính) |
4. Ví dụ minh họa
Ví dụ 1: Tính độ dài dây cung AB của đường tròn tâm O, bán kính 10 cm, biết góc AOB = 120°.
Lời giải:
$$AB = 2R\sin\frac{\alpha}{2} = 2 \times 10 \times \sin\frac{120°}{2} = 20 \times \sin 60° = 20 \times \frac{\sqrt{3}}{2} = 10\sqrt{3} \text{ cm}$$
Đáp án: $AB = 10\sqrt{3}$ cm (≈ 17.32 cm)
Ví dụ 2: Đường tròn có bán kính 8 cm, dây cung AB = 8 cm. Tính góc ở tâm.
Lời giải:
$$2R\sin\frac{\alpha}{2} = AB$$
$$\sin\frac{\alpha}{2} = \frac{8}{2 \times 8} = 0.5$$
$$\frac{\alpha}{2} = 30°$$
$$\alpha = 60°$$
Đáp án: $\alpha = 60°$
5. So sánh độ dài cung và dây cung
Với cùng góc ở tâm $\alpha < 180°$:
- Độ dài cung > Độ dài dây cung (vì đường cong dài hơn đường thẳng)
- Khi $\alpha \to 0$: độ dài cung ≈ độ dài dây cung
- Khi $\alpha = 180°$:
- Độ dài cung = $\pi R$ (nửa chu vi)
- Độ dài dây cung = $2R$ (đường kính)
IV. Công Thức Tính Số Đo Cung
1. Công thức tính số đo cung (góc ở tâm)
Khi biết độ dài cung và bán kính:
$$\alpha = \frac{l}{R} \text{ (radian)}$$
$$\alpha = \frac{180l}{\pi R} \text{ (độ)}$$
Trong đó:
- $\alpha$: góc ở tâm (số đo cung)
- $l$: độ dài cung
- $R$: bán kính
2. Công thức tính từ dây cung
Khi biết độ dài dây cung AB và bán kính R:
$$\sin\frac{\alpha}{2} = \frac{AB}{2R}$$
$$\Rightarrow \alpha = 2\arcsin\left(\frac{AB}{2R}\right)$$
3. Ví dụ
Ví dụ 1: Dây cung AB = 6 cm, bán kính R = 5 cm. Tính góc ở tâm.
Lời giải:
$$\sin\frac{\alpha}{2} = \frac{6}{2 \times 5} = \frac{6}{10} = 0.6$$
$$\frac{\alpha}{2} = \arcsin(0.6) \approx 36.87°$$
$$\alpha \approx 73.74°$$
Đáp án: $\alpha \approx 73.74°$
Ví dụ 2: Độ dài cung là $8\pi$ cm, bán kính 12 cm. Tính góc ở tâm bằng độ.
Lời giải:
$$\alpha = \frac{180l}{\pi R} = \frac{180 \times 8\pi}{\pi \times 12} = \frac{1440}{12} = 120°$$
Đáp án: $\alpha = 120°$
V. Công Thức Tính Diện Tích Hình Quạt Tròn
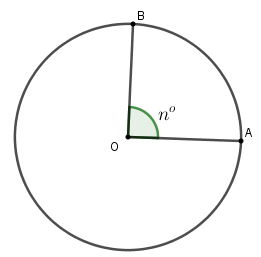
1. Khái niệm hình quạt tròn
Hình quạt tròn là phần hình phẳng được giới hạn bởi:
- Hai bán kính OA và OB
- Cung AB nối hai đầu mút của hai bán kính
Góc ở tâm $\alpha$ (góc AOB) quyết định độ lớn của hình quạt tròn.
2. Công thức cơ bản
a) Góc tính bằng radian:
$$S = \frac{1}{2}R^2\alpha$$
b) Góc tính bằng độ:
$$S = \frac{\pi R^2 \alpha}{360}$$
c) Khi biết độ dài cung l:
$$S = \frac{1}{2}lR$$
Trong đó:
- $S$: diện tích hình quạt tròn
- $R$: bán kính
- $\alpha$: góc ở tâm
- $l$: độ dài cung
Chứng minh công thức c):
Từ $l = R\alpha$ (radian), ta có $\alpha = \frac{l}{R}$
Thay vào công thức a):
$$S = \frac{1}{2}R^2 \times \frac{l}{R} = \frac{1}{2}lR$$
3. Bảng công thức tổng hợp
| Đại lượng cần tìm | Công thức (radian) | Công thức (độ) |
|---|---|---|
| Diện tích $S$ | $S = \frac{1}{2}R^2\alpha$ | $S = \frac{\pi R^2\alpha}{360}$ |
| Bán kính $R$ | $R = \sqrt{\frac{2S}{\alpha}}$ | $R = \sqrt{\frac{360S}{\pi\alpha}}$ |
| Góc $\alpha$ | $\alpha = \frac{2S}{R^2}$ | $\alpha = \frac{360S}{\pi R^2}$ |
4. Các trường hợp đặc biệt
| Góc ở tâm | Diện tích hình quạt |
|---|---|
| $\alpha = 360°$ (toàn phần) | $S = \pi R^2$ (diện tích hình tròn) |
| $\alpha = 180°$ (nửa hình tròn) | $S = \frac{\pi R^2}{2}$ |
| $\alpha = 90°$ (1/4 hình tròn) | $S = \frac{\pi R^2}{4}$ |
| $\alpha = 60°$ | $S = \frac{\pi R^2}{6}$ |
| $\alpha = 45°$ | $S = \frac{\pi R^2}{8}$ |
5. Ví dụ minh họa
Ví dụ 1: Tính diện tích hình quạt tròn có bán kính 8 cm, góc ở tâm 45°.
Lời giải:
$$S = \frac{\pi R^2\alpha}{360} = \frac{\pi \times 64 \times 45}{360} = \frac{2880\pi}{360} = 8\pi \text{ cm}^2$$
Đáp án: $S = 8\pi$ cm² (≈ 25.13 cm²)
Ví dụ 2: Hình quạt có bán kính 6 cm, độ dài cung $4\pi$ cm. Tính diện tích.
Lời giải:
$$S = \frac{1}{2}lR = \frac{1}{2} \times 4\pi \times 6 = 12\pi \text{ cm}^2$$
Đáp án: $S = 12\pi$ cm² (≈ 37.7 cm²)
Ví dụ 3: Diện tích hình quạt là $25\pi$ cm², bán kính 10 cm. Tính góc ở tâm.
Lời giải:
$$\alpha = \frac{360S}{\pi R^2} = \frac{360 \times 25\pi}{\pi \times 100} = \frac{9000}{100} = 90°$$
Đáp án: $\alpha = 90°$
Ví dụ 4: Hình quạt có diện tích $18\pi$ cm², góc ở tâm 120°. Tính bán kính.
Lời giải:
$$R = \sqrt{\frac{360S}{\pi\alpha}} = \sqrt{\frac{360 \times 18\pi}{\pi \times 120}} = \sqrt{\frac{6480}{120}} = \sqrt{54} = 3\sqrt{6} \text{ cm}$$
Đáp án: $R = 3\sqrt{6}$ cm (≈ 7.35 cm)
VI. Công Thức Tính Chu Vi Hình Quạt Tròn
Công thức
Chu vi hình quạt tròn bao gồm 2 bán kính và 1 cung:
$$P = 2R + l$$
Hoặc:
$$P = 2R + R\alpha = R(2 + \alpha)$$
(với $\alpha$ tính bằng radian)
$$P = 2R + \frac{\pi R\alpha}{180}$$
(với $\alpha$ tính bằng độ)
Trong đó:
- $P$: chu vi hình quạt
- $R$: bán kính
- $l$: độ dài cung
- $\alpha$: góc ở tâm
Ví dụ
Ví dụ 1: Tính chu vi hình quạt tròn có bán kính 5 cm, góc ở tâm 60°.
Lời giải:
- Độ dài cung: $l = \frac{\pi \times 5 \times 60}{180} = \frac{300\pi}{180} = \frac{5\pi}{3}$ cm
- Chu vi: $P = 2 \times 5 + \frac{5\pi}{3} = 10 + \frac{5\pi}{3}$ cm
Đáp án: $P = 10 + \frac{5\pi}{3}$ cm (≈ 15.24 cm)
Ví dụ 2: Hình quạt có bán kính 12 cm, chu vi 36 cm. Tính góc ở tâm.
Lời giải:
- Từ $P = 2R + l$: $$36 = 2 \times 12 + l$$ $$l = 36 – 24 = 12 \text{ cm}$$
- Góc ở tâm: $$\alpha = \frac{l}{R} = \frac{12}{12} = 1 \text{ rad}$$
Đổi sang độ: $\alpha = 1 \times \frac{180}{\pi} \approx 57.3°$
Đáp án: $\alpha = 1$ rad ≈ 57.3°
VII. Công Thức Tính Diện Tích Cung Tròn (Hình Viên Phân)
1. Khái niệm hình viên phân
Hình viên phân (hay còn gọi là cung tròn) là phần hình phẳng giới hạn bởi:
- Một cung tròn
- Dây cung nối hai đầu mút của cung đó
Công thức tổng quát:
$$\text{Hình viên phân} = \text{Hình quạt} – \text{Tam giác}$$
2. Công thức
$$S_{\text{viên phân}} = S_{\text{quạt}} – S_{\text{tam giác}}$$
$$S_{\text{viên phân}} = \frac{1}{2}R^2(\alpha – \sin\alpha)$$
(với $\alpha$ tính bằng radian)
Hoặc với góc tính bằng độ:
$$S_{\text{viên phân}} = \frac{\pi R^2\alpha}{360} – \frac{1}{2}R^2\sin\alpha$$
3. Công thức tam giác trong hình quạt
Diện tích tam giác OAB (với O là tâm, A và B là hai đầu cung):
$$S_{\text{tam giác}} = \frac{1}{2}R^2\sin\alpha$$
4. Ví dụ minh họa
Ví dụ 1: Tính diện tích hình viên phân có bán kính 10 cm, góc ở tâm 60°.
Lời giải:
- Đổi góc: $\alpha = 60° = \frac{\pi}{3}$ rad
- Diện tích hình quạt: $$S_{\text{quạt}} = \frac{1}{2} \times 10^2 \times \frac{\pi}{3} = \frac{50\pi}{3} \text{ cm}^2$$
- Diện tích tam giác: $$S_{\text{tam giác}} = \frac{1}{2} \times 10^2 \times \sin 60° = 50 \times \frac{\sqrt{3}}{2} = 25\sqrt{3} \text{ cm}^2$$
- Diện tích hình viên phân: $$S_{\text{viên phân}} = \frac{50\pi}{3} – 25\sqrt{3} \text{ cm}^2$$
$$S_{\text{viên phân}} \approx 52.36 – 43.30 = 9.06 \text{ cm}^2$$
Đáp án: $S = \frac{50\pi}{3} – 25\sqrt{3}$ cm² ≈ 9.06 cm²
Ví dụ 2: Hình viên phân có bán kính 8 cm, góc ở tâm 90°. Tính diện tích.
Lời giải:
$$S_{\text{viên phân}} = \frac{\pi \times 64 \times 90}{360} – \frac{1}{2} \times 64 \times \sin 90°$$
$$S = 16\pi – 32 \text{ cm}^2$$
$$S \approx 50.27 – 32 = 18.27 \text{ cm}^2$$
Đáp án: $S = 16\pi – 32$ cm² ≈ 18.27 cm²
VIII. Bảng Tổng Hợp Công Thức
Bảng 1: Công thức về cung tròn
| Tên | Công thức (radian) | Công thức (độ) |
|---|---|---|
| Độ dài cung | $l = R\alpha$ | $l = \frac{\pi R\alpha}{180}$ |
| Dây cung | $AB = 2R\sin\frac{\alpha}{2}$ | $AB = 2R\sin\frac{\alpha}{2}$ |
| Số đo góc | $\alpha = \frac{l}{R}$ | $\alpha = \frac{180l}{\pi R}$ |
Bảng 2: Công thức về hình quạt tròn
| Tên | Công thức (radian) | Công thức (độ) |
|---|---|---|
| Diện tích quạt | $S = \frac{1}{2}R^2\alpha$ | $S = \frac{\pi R^2\alpha}{360}$ |
| Diện tích quạt (theo cung) | $S = \frac{1}{2}lR$ | $S = \frac{1}{2}lR$ |
| Chu vi quạt | $P = R(2 + \alpha)$ | $P = 2R + \frac{\pi R\alpha}{180}$ |
| Diện tích viên phân | $S = \frac{1}{2}R^2(\alpha – \sin\alpha)$ | $S = \frac{\pi R^2\alpha}{360} – \frac{1}{2}R^2\sin\alpha$ |
Bảng 3: Giá trị đặc biệt
| Góc | Độ dài cung | Diện tích quạt |
|---|---|---|
| 30° | $\frac{\pi R}{6}$ | $\frac{\pi R^2}{12}$ |
| 45° | $\frac{\pi R}{4}$ | $\frac{\pi R^2}{8}$ |
| 60° | $\frac{\pi R}{3}$ | $\frac{\pi R^2}{6}$ |
| 90° | $\frac{\pi R}{2}$ | $\frac{\pi R^2}{4}$ |
| 120° | $\frac{2\pi R}{3}$ | $\frac{\pi R^2}{3}$ |
| 180° | $\pi R$ | $\frac{\pi R^2}{2}$ |
| 360° | $2\pi R$ | $\pi R^2$ |
IX. Bài Tập Vận Dụng
Dạng 1: Bài tập về cung tròn
Bài 1: Bánh xe có bán kính 30 cm quay được 120°. Tính quãng đường bánh xe đi được.
Lời giải:
Quãng đường bánh xe đi được = Độ dài cung
$$l = \frac{\pi R\alpha}{180} = \frac{\pi \times 30 \times 120}{180} = 20\pi \text{ cm}$$
Đáp án: $20\pi$ cm ≈ 62.83 cm
Bài 2: Đường tròn có bán kính 15 cm. Tính độ dài cung ứng với góc ở tâm 150°.
Lời giải:
$$l = \frac{\pi \times 15 \times 150}{180} = \frac{2250\pi}{180} = 12.5\pi \text{ cm}$$
Đáp án: $12.5\pi$ cm ≈ 39.27 cm
Bài 3: Cung tròn có độ dài $18\pi$ cm, góc ở tâm 90°. Tính bán kính.
Lời giải:
$$R = \frac{180l}{\pi\alpha} = \frac{180 \times 18\pi}{\pi \times 90} = \frac{3240}{90} = 36 \text{ cm}$$
Đáp án: R = 36 cm
Bài 4: Kim phút của đồng hồ dài 12 cm. Tính quãng đường đầu kim phút đi được trong 20 phút.
Lời giải:
- 20 phút = $\frac{20}{60}$ vòng = $\frac{1}{3}$ vòng
- Góc quay: $\alpha = \frac{1}{3} \times 360° = 120°$
- Quãng đường:
$$l = \frac{\pi \times 12 \times 120}{180} = 8\pi \text{ cm}$$
Đáp án: $8\pi$ cm ≈ 25.13 cm
Bài 5: Đường tròn có chu vi 60π cm. Tính độ dài cung ứng với góc ở tâm 72°.
Lời giải:
- Từ chu vi: $2\pi R = 60\pi \Rightarrow R = 30$ cm
- Độ dài cung:
$$l = \frac{\pi \times 30 \times 72}{180} = 12\pi \text{ cm}$$
Đáp án: $12\pi$ cm ≈ 37.7 cm
Bài 6: Hai cung tròn cùng góc ở tâm 60° có độ dài lần lượt là $5\pi$ cm và $8\pi$ cm. Tính tỷ số hai bán kính.
Lời giải:
- Cung 1: $l_1 = R_1\alpha \Rightarrow 5\pi = R_1 \times \frac{\pi}{3} \Rightarrow R_1 = 15$ cm
- Cung 2: $l_2 = R_2\alpha \Rightarrow 8\pi = R_2 \times \frac{\pi}{3} \Rightarrow R_2 = 24$ cm
- Tỷ số: $\frac{R_1}{R_2} = \frac{15}{24} = \frac{5}{8}$
Đáp án: Tỷ số bán kính là 5:8
Bài 7: Độ dài cung AB là $10\pi$ cm. Nếu tăng bán kính lên gấp đôi và giữ nguyên góc ở tâm thì độ dài cung mới là bao nhiêu?
Lời giải:
Vì $l = R\alpha$, khi tăng R lên gấp đôi thì độ dài cung cũng tăng gấp đôi:
$$l_{\text{mới}} = 2 \times 10\pi = 20\pi \text{ cm}$$
Đáp án: $20\pi$ cm
Bài 8: Đường tròn có bán kính 20 cm. Hai điểm A, B trên đường tròn sao cho dây AB = $20\sqrt{2}$ cm. Tính độ dài cung nhỏ AB.
Lời giải:
- Tính góc ở tâm từ dây cung: $$AB = 2R\sin\frac{\alpha}{2}$$ $$20\sqrt{2} = 2 \times 20 \times \sin\frac{\alpha}{2}$$ $$\sin\frac{\alpha}{2} = \frac{\sqrt{2}}{2}$$ $$\frac{\alpha}{2} = 45° \Rightarrow \alpha = 90°$$
- Độ dài cung: $$l = \frac{\pi \times 20 \times 90}{180} = 10\pi \text{ cm}$$
Đáp án: $10\pi$ cm ≈ 31.42 cm
Dạng 2: Bài tập về hình quạt tròn
Bài 9: Một cái quạt có bán kính 25 cm, góc giữa 2 cánh quạt là 30°. Tính diện tích 1 cánh quạt.
Lời giải:
$$S = \frac{\pi R^2\alpha}{360} = \frac{\pi \times 625 \times 30}{360} = \frac{18750\pi}{360} = \frac{625\pi}{12} \text{ cm}^2$$
Đáp án: $\frac{625\pi}{12}$ cm² ≈ 163.62 cm²
Bài 10: Hình quạt có chu vi 28 cm, bán kính 7 cm. Tính diện tích hình quạt.
Lời giải:
- Từ chu vi tính độ dài cung: $$P = 2R + l \Rightarrow 28 = 14 + l \Rightarrow l = 14 \text{ cm}$$
- Diện tích: $$S = \frac{1}{2}lR = \frac{1}{2} \times 14 \times 7 = 49 \text{ cm}^2$$
Đáp án: S = 49 cm²
Bài 11: Logo hình quạt có diện tích $36\pi$ cm², góc ở tâm 120°. Tính bán kính.
Lời giải:
$$R = \sqrt{\frac{360S}{\pi\alpha}} = \sqrt{\frac{360 \times 36\pi}{\pi \times 120}} = \sqrt{\frac{12960}{120}} = \sqrt{108} = 6\sqrt{3} \text{ cm}$$
Đáp án: $R = 6\sqrt{3}$ cm ≈ 10.39 cm
Bài 12: Hình quạt tròn có bán kính 10 cm, diện tích $50\pi$ cm². Tính độ dài cung và chu vi hình quạt.
Lời giải:
- Tính độ dài cung từ diện tích: $$S = \frac{1}{2}lR \Rightarrow 50\pi = \frac{1}{2} \times l \times 10$$ $$l = 10\pi \text{ cm}$$
- Chu vi: $$P = 2R + l = 20 + 10\pi \text{ cm}$$
Đáp án: $l = 10\pi$ cm, $P = 20 + 10\pi$ cm ≈ 51.42 cm
Bài 13: Từ hình tròn bán kính 12 cm, cắt bỏ hình quạt có góc ở tâm 90°. Tính diện tích phần còn lại.
Lời giải:
- Diện tích hình tròn: $$S_{\text{tròn}} = \pi \times 12^2 = 144\pi \text{ cm}^2$$
- Diện tích hình quạt bị cắt: $$S_{\text{quạt}} = \frac{\pi \times 144 \times 90}{360} = 36\pi \text{ cm}^2$$
- Diện tích còn lại: $$S = 144\pi – 36\pi = 108\pi \text{ cm}^2$$
Đáp án: $108\pi$ cm² ≈ 339.29 cm²
Bài 14: Hai hình quạt có cùng bán kính 15 cm, góc ở tâm lần lượt là 60° và 120°. Tính tỷ số diện tích của chúng.
Lời giải:
Vì $S = \frac{\pi R^2\alpha}{360}$ nên với cùng bán kính:
$$\frac{S_1}{S_2} = \frac{\alpha_1}{\alpha_2} = \frac{60}{120} = \frac{1}{2}$$
Đáp án: Tỷ số diện tích là 1:2
Bài 15: Hình quạt có chu vi 40 cm, diện tích 75 cm². Tính bán kính và góc ở tâm.
Lời giải:
Từ $P = 2R + l$ và $S = \frac{1}{2}lR$:
$$l = P – 2R = 40 – 2R$$
$$S = \frac{1}{2}(40 – 2R)R = 75$$
$$20R – R^2 = 75$$
$$R^2 – 20R + 75 = 0$$
$$(R – 5)(R – 15) = 0$$
$$R = 5 \text{ hoặc } R = 15$$
- Nếu $R = 5$: $l = 40 – 10 = 30$ cm → $\alpha = \frac{30}{5} = 6$ rad ≈ 343.77° (vô lý vì > 360°)
- Nếu $R = 15$: $l = 40 – 30 = 10$ cm → $\alpha = \frac{10}{15} = \frac{2}{3}$ rad ≈ 38.2°
Đáp án: $R = 15$ cm, $\alpha = \frac{2}{3}$ rad ≈ 38.2°
Bài 16: Hình quạt tròn có diện tích bằng $\frac{1}{6}$ diện tích hình tròn tương ứng. Tính góc ở tâm.
Lời giải:
- Diện tích hình tròn: $S_{\text{tròn}} = \pi R^2$
- Diện tích hình quạt: $S_{\text{quạt}} = \frac{1}{6}\pi R^2$
Từ công thức: $$\frac{\pi R^2\alpha}{360} = \frac{\pi R^2}{6}$$
$$\frac{\alpha}{360} = \frac{1}{6}$$
$$\alpha = 60°$$
Đáp án: $\alpha = 60°$
X. Kết Luận
Tổng kết
Bài viết đã tổng hợp đầy đủ các công thức về cung tròn và hình quạt tròn:
Độ dài cung tròn:
- $l = R\alpha$ (radian)
- $l = \frac{\pi R\alpha}{180}$ (độ)
Độ dài dây cung:
- $AB = 2R\sin\frac{\alpha}{2}$
Số đo cung (góc ở tâm):
- $\alpha = \frac{l}{R}$ (radian)
- $\alpha = \frac{180l}{\pi R}$ (độ)
Diện tích hình quạt tròn:
- $S = \frac{1}{2}R^2\alpha$ (radian)
- $S = \frac{\pi R^2\alpha}{360}$ (độ)
- $S = \frac{1}{2}lR$ (khi biết độ dài cung)
Chu vi hình quạt tròn:
- $P = 2R + l$
Diện tích hình viên phân:
- $S = \frac{1}{2}R^2(\alpha – \sin\alpha)$
Mẹo nhớ
Công thức độ dài cung: “l = R × α” (với radian)
Công thức diện tích quạt: “S = 1/2 × R² × α” hoặc “S = 1/2 × l × R”
Luôn chú ý đơn vị góc: Độ hay radian? Chuyển đổi đúng!
Chu vi quạt = 2 bán kính + 1 cung
Ứng dụng thực tế
Các công thức này được sử dụng rộng rãi trong:
- Thiết kế đồ họa: Logo, biểu tượng hình quạt
- Kiến trúc: Mái vòm, cổng vòm, cầu thang xoắn
- Cơ khí: Bánh răng, bánh xe, quạt, đĩa
- Toán học: Lượng giác, hình học phẳng và không gian
- Đời sống: Đo đạc, tính toán quãng đường

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
