Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU
- 1. Khái niệm cơ bản
- 2. So sánh nhanh
- II. VECTƠ PHÁP TUYẾN CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
- 1. VTPT của đường thẳng trong mặt phẳng
- 2. VTPT của mặt phẳng trong không gian
- 3. Cách tìm VTPT của mặt phẳng
- 4. Tính chất của VTPT
- III. VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG
- 1. Định nghĩa
- 2. Cách tìm VTCP trong mặt phẳng
- 3. Cách tìm VTCP trong không gian
- IV. MỐI LIÊN HỆ GIỮA VTPT VÀ VTCP
- 1. Trong mặt phẳng
- 2. Trong không gian
- V. BẢNG CÔNG THỨC TÓM TẮT
- A. Vectơ pháp tuyến
- B. Vectơ chỉ phương
- C. Mối liên hệ
- VI. CÁCH TÌM NHANH
- 1. Tìm VTPT
- 2. Tìm VTCP
- 3. Mẹo nhớ
- VII. BÀI TẬP MẪU
- VIII. MẸO VÀ LƯU Ý
- 1. Các sai lầm thường gặp
- 2. Kiểm tra nhanh kết quả
- IX. KẾT LUẬN
- Tổng kết
- Công thức quan trọng nhất
- Tài liệu tham khảo
I. GIỚI THIỆU
1. Khái niệm cơ bản
Vectơ pháp tuyến (VTPT):
Vectơ pháp tuyến của một đường thẳng hoặc mặt phẳng là vectơ có giá vuông góc với đường thẳng hoặc mặt phẳng đó.
- Ký hiệu: $\vec{n}$ (từ chữ “normal” trong tiếng Anh)
- Đặc điểm: Vuông góc với mọi vectơ nằm trên đường thẳng/mặt phẳng
- Vai trò: Xác định hướng vuông góc, lập phương trình

Vectơ chỉ phương (VTCP):
Vectơ chỉ phương của một đường thẳng là vectơ có giá song song hoặc trùng với đường thẳng đó.
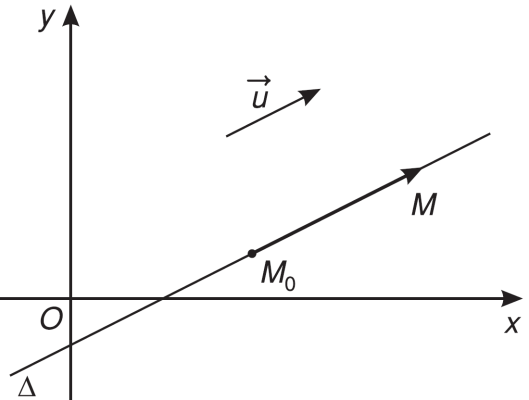
- Ký hiệu: $\vec{u}$ (từ chữ “direction” – hướng)
- Đặc điểm: Song song với đường thẳng
- Vai trò: Chỉ hướng của đường thẳng, lập phương trình tham số
Vai trò trong hình học giải tích:
Hai loại vectơ này là công cụ quan trọng nhất để:
- Lập phương trình đường thẳng và mặt phẳng
- Xác định vị trí tương đối (song song, vuông góc, cắt nhau)
- Tính góc giữa các đối tượng hình học
- Tìm giao tuyến, giao điểm
2. So sánh nhanh
| Tiêu chí | Vectơ Pháp Tuyến (VTPT) | Vectơ Chỉ Phương (VTCP) |
|---|---|---|
| Ký hiệu | $\vec{n}$ | $\vec{u}$ |
| Quan hệ với đối tượng | Vuông góc | Song song |
| Dùng cho | Đường thẳng (mặt phẳng), Mặt phẳng (không gian) | Đường thẳng (mặt phẳng và không gian) |
| Phương trình liên quan | Phương trình tổng quát | Phương trình tham số, chính tắc |
| Công thức kiểm tra | $\vec{n} \cdot \vec{v} = 0$ với $\vec{v}$ trên đối tượng | $\vec{u} = k\vec{v}$ với $\vec{v}$ song song |
II. VECTƠ PHÁP TUYẾN CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
1. VTPT của đường thẳng trong mặt phẳng
Định nghĩa:
Vectơ $\vec{n}$ được gọi là vectơ pháp tuyến của đường thẳng $d$ trong mặt phẳng nếu: $$\vec{n} \perp d$$
Hay nói cách khác, $\vec{n}$ vuông góc với mọi vectơ chỉ phương của $d$.
Công thức từ phương trình:
Đường thẳng có phương trình tổng quát: $$ax + by + c = 0$$
Thì có vectơ pháp tuyến: $$\boxed{\vec{n} = (a; b)}$$
Cách nhớ: “Đọc hệ số của x và y”
Ví dụ 1: Tìm VTPT của đường thẳng $d: 2x – 3y + 5 = 0$
Lời giải:
- Hệ số: $a = 2$, $b = -3$
- Vectơ pháp tuyến: $\vec{n} = (2; -3)$
Kiểm tra: Nếu $\vec{u}$ là VTCP của $d$ thì $\vec{n} \cdot \vec{u} = 0$ ✓
Tính chất quan trọng:
✅ Tính chất 1: Nếu $\vec{n} = (a; b)$ là VTPT thì $k\vec{n} = (ka; kb)$ với $k \neq 0$ cũng là VTPT
Ví dụ: $\vec{n} = (2; -3)$ → $2\vec{n} = (4; -6)$ cũng là VTPT
✅ Tính chất 2: $\vec{n}$ vuông góc với mọi vectơ chỉ phương của đường thẳng
Hay: $\vec{n} \cdot \vec{u} = 0$ với mọi VTCP $\vec{u}$ của $d$
✅ Tính chất 3: Đường thẳng có vô số VTPT (tất cả cùng phương với nhau)
2. VTPT của mặt phẳng trong không gian
Định nghĩa:
Vectơ $\vec{n}$ được gọi là vectơ pháp tuyến của mặt phẳng $(P)$ nếu: $$\vec{n} \perp (P)$$
Hay $\vec{n}$ vuông góc với mọi vectơ nằm trong mặt phẳng $(P)$.
Công thức từ phương trình:
Mặt phẳng có phương trình tổng quát: $$Ax + By + Cz + D = 0$$
Thì có vectơ pháp tuyến: $$\boxed{\vec{n} = (A; B; C)}$$
Cách nhớ: “Đọc hệ số của x, y và z”
Ví dụ 2: Tìm VTPT của mặt phẳng $(P): 2x – y + 3z – 4 = 0$
Lời giải:
- Hệ số: $A = 2$, $B = -1$, $C = 3$
- Vectơ pháp tuyến: $\vec{n} = (2; -1; 3)$
Lưu ý: Hệ số $D = -4$ không ảnh hưởng đến VTPT
3. Cách tìm VTPT của mặt phẳng
Phương pháp 1: Từ phương trình tổng quát
Đây là cách đơn giản nhất – chỉ cần đọc hệ số.
Ví dụ 3:
- $(P): 3x + 4y – 5z + 7 = 0$ → $\vec{n} = (3; 4; -5)$
- $(Q): x – 2z = 0$ → $\vec{n} = (1; 0; -2)$
- $(R): y + z – 1 = 0$ → $\vec{n} = (0; 1; 1)$
Phương pháp 2: Qua 3 điểm không thẳng hàng
Mặt phẳng đi qua ba điểm $A$, $B$, $C$ có VTPT: $$\boxed{\vec{n} = \overrightarrow{AB} \times \overrightarrow{AC}}$$
Công thức tích có hướng: $$\overrightarrow{AB} \times \overrightarrow{AC} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ x_{AB} & y_{AB} & z_{AB} \\ x_{AC} & y_{AC} & z_{AC} \end{vmatrix}$$
Ví dụ 4: Tìm VTPT của mặt phẳng qua $A(1; 0; 0)$, $B(0; 1; 0)$, $C(0; 0; 1)$
Lời giải:
Bước 1: Tính các vectơ
- $\overrightarrow{AB} = (0-1; 1-0; 0-0) = (-1; 1; 0)$
- $\overrightarrow{AC} = (0-1; 0-0; 1-0) = (-1; 0; 1)$
Bước 2: Tính tích có hướng $$\vec{n} = \overrightarrow{AB} \times \overrightarrow{AC} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ -1 & 1 & 0 \\ -1 & 0 & 1 \end{vmatrix}$$
$$= \vec{i}(1 \cdot 1 – 0 \cdot 0) – \vec{j}((-1) \cdot 1 – 0 \cdot (-1)) + \vec{k}((-1) \cdot 0 – 1 \cdot (-1))$$
$$= \vec{i}(1) – \vec{j}(-1) + \vec{k}(1) = (1; 1; 1)$$
Đáp án: $\vec{n} = (1; 1; 1)$
Phương pháp 3: Qua 1 điểm và 2 VTCP
Nếu mặt phẳng $(P)$ đi qua điểm $M$ và có hai vectơ chỉ phương không cùng phương $\vec{u_1}$, $\vec{u_2}$, thì: $$\boxed{\vec{n} = \vec{u_1} \times \vec{u_2}}$$
Ví dụ 5: Mặt phẳng qua $M(1; 2; 3)$ và có hai VTCP $\vec{u_1} = (1; 0; 1)$, $\vec{u_2} = (0; 1; 1)$. Tìm VTPT.
Lời giải: $$\vec{n} = \vec{u_1} \times \vec{u_2} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 1 & 0 & 1 \\ 0 & 1 & 1 \end{vmatrix}$$
$$= \vec{i}(0-1) – \vec{j}(1-0) + \vec{k}(1-0) = (-1; -1; 1)$$
Có thể rút gọn: $\vec{n} = (1; 1; -1)$ (nhân với -1)
Phương pháp 4: Mặt phẳng vuông góc với đường thẳng
Nếu mặt phẳng $(P)$ vuông góc với đường thẳng $d$, thì: $$\text{VTCP của } d \text{ chính là VTPT của } (P)$$
Ví dụ 6: Mặt phẳng $(P)$ đi qua $M(1; 2; 3)$ và vuông góc với đường thẳng $d$ có VTCP $\vec{u} = (2; -1; 3)$. Tìm VTPT của $(P)$.
Lời giải:
- VTPT của $(P)$ chính là VTCP của $d$: $\vec{n} = (2; -1; 3)$
4. Tính chất của VTPT
Tính chất 1: $\vec{n}$ vuông góc với mọi vectơ nằm trong mặt phẳng
Tức là: $\vec{n} \perp \overrightarrow{MN}$ với mọi $M$, $N$ thuộc mặt phẳng
Tính chất 2: Nếu $\vec{n}$ là VTPT thì $k\vec{n}$ ($k \neq 0$) cũng là VTPT
Tính chất 3: Điều kiện để hai mặt phẳng song song
$(P_1) // (P_2) \Leftrightarrow \vec{n_1} = k\vec{n_2}$ (hai VTPT cùng phương)
Tính chất 4: Điều kiện để hai mặt phẳng vuông góc
$(P_1) \perp (P_2) \Leftrightarrow \vec{n_1} \cdot \vec{n_2} = 0$ (hai VTPT vuông góc)
Tính chất 5: Kiểm tra điểm thuộc mặt phẳng
Nếu $A$, $B$ cùng thuộc $(P)$ thì: $$\vec{n} \cdot \overrightarrow{AB} = 0$$
III. VECTƠ CHỈ PHƯƠNG CỦA ĐƯỜNG THẲNG
1. Định nghĩa
Vectơ chỉ phương $\vec{u}$ của đường thẳng $d$ là vectơ có giá song song hoặc trùng với $d$.
Ý nghĩa: $\vec{u}$ chỉ hướng của đường thẳng, cho biết đường thẳng đi theo phương nào.
Tính chất cơ bản:
✅ $\vec{u}$ song song với đường thẳng $d$
✅ Nếu $\vec{u}$ là VTCP thì $k\vec{u}$ ($k \neq 0$) cũng là VTCP
✅ Một đường thẳng có vô số VTCP (tất cả cùng phương với nhau)
✅ Nếu $A$, $B$ thuộc $d$ thì $\overrightarrow{AB}$ là một VTCP của $d$
2. Cách tìm VTCP trong mặt phẳng
Phương pháp 1: Từ phương trình tổng quát
Đường thẳng có phương trình: $$ax + by + c = 0$$
Có VTPT: $\vec{n} = (a; b)$
Thì có VTCP: $$\boxed{\vec{u} = (-b; a) \text{ hoặc } \vec{u} = (b; -a)}$$
Mẹo nhớ: “Đổi chỗ hai số và đổi dấu một trong hai”
Ví dụ 7: Tìm VTCP của đường thẳng $d: 2x – 3y + 5 = 0$
Lời giải:
- VTPT: $\vec{n} = (2; -3)$
- VTCP: $\vec{u} = (3; 2)$ hoặc $\vec{u} = (-3; -2)$
Kiểm tra: $\vec{n} \cdot \vec{u} = 2 \times 3 + (-3) \times 2 = 6 – 6 = 0$ ✓
Phương pháp 2: Từ phương trình tham số
Đường thẳng có phương trình tham số: $$\begin{cases} x = x_0 + at \\ y = y_0 + bt \end{cases}$$
Thì có VTCP: $$\boxed{\vec{u} = (a; b)}$$
Cách nhớ: “Đọc hệ số của tham số t”
Ví dụ 8: Đường thẳng $d: \begin{cases} x = 1 + 2t \\ y = -3 + 5t \end{cases}$
Lời giải: VTCP là $\vec{u} = (2; 5)$
Phương pháp 3: Qua 2 điểm
Đường thẳng đi qua hai điểm $A(x_A; y_A)$ và $B(x_B; y_B)$ có VTCP: $$\boxed{\vec{u} = \overrightarrow{AB} = (x_B – x_A; y_B – y_A)}$$
Ví dụ 9: Đường thẳng qua $A(1; 2)$ và $B(4; 6)$
Lời giải: $$\vec{u} = \overrightarrow{AB} = (4-1; 6-2) = (3; 4)$$
3. Cách tìm VTCP trong không gian
Phương pháp 1: Từ phương trình tham số
Đường thẳng có phương trình tham số: $$\begin{cases} x = x_0 + at \\ y = y_0 + bt \\ z = z_0 + ct \end{cases}$$
Thì có VTCP: $$\boxed{\vec{u} = (a; b; c)}$$
Ví dụ 10: Đường thẳng $d: \begin{cases} x = 2 + 3t \\ y = -1 + 2t \\ z = 4 – t \end{cases}$
Lời giải: VTCP là $\vec{u} = (3; 2; -1)$
Phương pháp 2: Từ phương trình chính tắc
Đường thẳng có phương trình chính tắc: $$\frac{x – x_0}{a} = \frac{y – y_0}{b} = \frac{z – z_0}{c}$$
Thì có VTCP: $$\boxed{\vec{u} = (a; b; c)}$$
Cách nhớ: “Đọc các mẫu số”
Ví dụ 11: Đường thẳng $d: \frac{x-1}{2} = \frac{y+1}{-3} = \frac{z}{4}$
Lời giải: VTCP là $\vec{u} = (2; -3; 4)$
Phương pháp 3: Qua 2 điểm trong không gian
Đường thẳng đi qua hai điểm $A(x_A; y_A; z_A)$ và $B(x_B; y_B; z_B)$ có VTCP: $$\boxed{\vec{u} = \overrightarrow{AB} = (x_B – x_A; y_B – y_A; z_B – z_A)}$$
Ví dụ 12: Đường thẳng qua $A(1; 2; 3)$ và $B(4; 5; 7)$
Lời giải: $$\vec{u} = \overrightarrow{AB} = (3; 3; 4)$$
Phương pháp 4: Giao tuyến của 2 mặt phẳng
Đường thẳng $d$ là giao tuyến của hai mặt phẳng $(P_1)$ và $(P_2)$ có:
- VTPT của $(P_1)$: $\vec{n_1}$
- VTPT của $(P_2)$: $\vec{n_2}$
Thì VTCP của $d$: $$\boxed{\vec{u} = \vec{n_1} \times \vec{n_2}}$$
Giải thích: Vì $d$ nằm trong cả hai mặt phẳng nên $\vec{u}$ phải vuông góc với cả $\vec{n_1}$ và $\vec{n_2}$.
Ví dụ 13: Tìm VTCP của giao tuyến của:
- $(P_1): x + y + z = 0$
- $(P_2): x – y + 2z = 0$
Lời giải:
Bước 1: Xác định VTPT
- $\vec{n_1} = (1; 1; 1)$
- $\vec{n_2} = (1; -1; 2)$
Bước 2: Tính tích có hướng $$\vec{u} = \vec{n_1} \times \vec{n_2} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 1 & 1 & 1 \\ 1 & -1 & 2 \end{vmatrix}$$
$$= \vec{i}(2-(-1)) – \vec{j}(2-1) + \vec{k}(-1-1)$$ $$= \vec{i}(3) – \vec{j}(1) + \vec{k}(-2)$$ $$= (3; -1; -2)$$
Đáp án: $\vec{u} = (3; -1; -2)$
IV. MỐI LIÊN HỆ GIỮA VTPT VÀ VTCP
1. Trong mặt phẳng
Quan hệ vuông góc:
VTPT và VTCP của cùng một đường thẳng luôn vuông góc với nhau: $$\boxed{\vec{n} \perp \vec{u} \Leftrightarrow \vec{n} \cdot \vec{u} = 0}$$
Chứng minh: Vì $\vec{n}$ vuông góc với đường thẳng, mà $\vec{u}$ song song với đường thẳng, nên $\vec{n} \perp \vec{u}$.
Từ VTPT tìm VTCP:
Nếu $\vec{n} = (a; b)$ là VTPT của đường thẳng, thì: $$\boxed{\vec{u} = (-b; a) \text{ hoặc } (b; -a)}$$
Ví dụ 14:
- VTPT: $\vec{n} = (2; 3)$
- VTCP: $\vec{u} = (-3; 2)$ hoặc $(3; -2)$
Kiểm tra: $\vec{n} \cdot \vec{u} = 2 \times (-3) + 3 \times 2 = -6 + 6 = 0$ ✓
Từ VTCP tìm VTPT:
Nếu $\vec{u} = (a; b)$ là VTCP của đường thẳng, thì: $$\boxed{\vec{n} = (-b; a) \text{ hoặc } (b; -a)}$$
Ví dụ 15:
- VTCP: $\vec{u} = (4; 5)$
- VTPT: $\vec{n} = (-5; 4)$ hoặc $(5; -4)$
2. Trong không gian
Đối với đường thẳng:
- Một đường thẳng có vô số VTCP (tất cả cùng phương)
- Một đường thẳng có vô số VTPT (tất cả vuông góc với VTCP)
- Tất cả các VTPT của đường thẳng tạo thành một mặt phẳng vuông góc với đường thẳng
Đối với mặt phẳng:
- Một mặt phẳng có vô số VTPT (tất cả cùng phương)
- Một mặt phẳng có vô số VTCP (tất cả song song với mặt phẳng)
- VTCP và VTPT của mặt phẳng luôn vuông góc: $\vec{n} \cdot \vec{u} = 0$
Mối liên hệ quan trọng:
Nếu đường thẳng $d$ vuông góc với mặt phẳng $(P)$: $$\text{VTCP của } d = \text{VTPT của } (P)$$
Ví dụ: Đường thẳng $d$ vuông góc với $(P): 2x – y + 3z = 0$
- VTPT của $(P)$: $\vec{n} = (2; -1; 3)$
- VTCP của $d$: $\vec{u} = (2; -1; 3)$
Nếu đường thẳng $d$ nằm trong mặt phẳng $(P)$: $$\text{VTCP của } d \perp \text{VTPT của } (P)$$
Hay: $\vec{u} \cdot \vec{n} = 0$
V. BẢNG CÔNG THỨC TÓM TẮT
A. Vectơ pháp tuyến
| Đối tượng | Phương trình | VTPT | Ghi chú |
|---|---|---|---|
| Đường thẳng (mặt phẳng) | $ax + by + c = 0$ | $\vec{n} = (a; b)$ | Đọc hệ số x, y |
| Mặt phẳng (không gian) | $Ax + By + Cz + D = 0$ | $\vec{n} = (A; B; C)$ | Đọc hệ số x, y, z |
| Mp qua 3 điểm | $A$, $B$, $C$ | $\vec{n} = \overrightarrow{AB} \times \overrightarrow{AC}$ | Tích có hướng |
| Mp qua M, có 2 VTCP | $M$, $\vec{u_1}$, $\vec{u_2}$ | $\vec{n} = \vec{u_1} \times \vec{u_2}$ | Tích có hướng |
| Mp vuông góc đường thẳng | $(P) \perp d$, $\vec{u}$ là VTCP của $d$ | $\vec{n} = \vec{u}$ | VTCP = VTPT |
B. Vectơ chỉ phương
| Đối tượng | Phương trình/Điều kiện | VTCP | Ghi chú |
|---|---|---|---|
| Đ.thẳng từ VTPT (mp) | $ax+by+c=0$, $\vec{n}=(a;b)$ | $\vec{u} = (-b; a)$ | Đổi chỗ, đổi dấu |
| PT tham số (mp) | $\begin{cases} x=x_0+at \\ y=y_0+bt \end{cases}$ | $\vec{u} = (a; b)$ | Đọc hệ số t |
| PT chính tắc (kg) | $\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$ | $\vec{u} = (a; b; c)$ | Đọc mẫu số |
| PT tham số (kg) | $\begin{cases} x=x_0+at \\ y=y_0+bt \\ z=z_0+ct \end{cases}$ | $\vec{u} = (a; b; c)$ | Đọc hệ số t |
| Qua 2 điểm | $A$, $B$ | $\vec{u} = \overrightarrow{AB}$ | Cuối trừ đầu |
| Giao 2 mặt phẳng | $(P_1)$: $\vec{n_1}$, $(P_2)$: $\vec{n_2}$ | $\vec{u} = \vec{n_1} \times \vec{n_2}$ | Tích có hướng |
C. Mối liên hệ
| Không gian | Quan hệ | Công thức |
|---|---|---|
| Mặt phẳng Oxy | VTPT ⊥ VTCP | $\vec{n} \cdot \vec{u} = 0$ |
| Mặt phẳng Oxy | Từ VTPT → VTCP | $\vec{n}=(a;b)$ → $\vec{u}=(-b;a)$ |
| Mặt phẳng Oxy | Từ VTCP → VTPT | $\vec{u}=(a;b)$ → $\vec{n}=(-b;a)$ |
| Không gian Oxyz | Đường ⊥ Mặt | VTCP đường = VTPT mặt |
| Không gian Oxyz | Đường ⊂ Mặt | $\vec{u} \cdot \vec{n} = 0$ |
VI. CÁCH TÌM NHANH
1. Tìm VTPT
QUY TRÌNH 3 BƯỚC:
✅ Bước 1: Xác định dạng bài
- Có phương trình tổng quát? → Đọc hệ số
- Có 3 điểm không thẳng hàng? → Tích có hướng
- Mặt phẳng vuông góc với đường thẳng? → Lấy VTCP của đường
✅ Bước 2: Áp dụng công thức tương ứng
- Phương trình: $\vec{n} = (A; B; C)$
- Ba điểm: $\vec{n} = \overrightarrow{AB} \times \overrightarrow{AC}$
- Vuông góc: $\vec{n} = \vec{u}$ (VTCP của đường)
✅ Bước 3: Rút gọn (nếu cần)
- Chia cho ước chung lớn nhất
- Hoặc nhân với -1 để có số dương đầu tiên
Ví dụ nhanh:
- $(P): 6x – 9y + 12z = 0$ → $\vec{n} = (6; -9; 12)$ → Rút gọn: $\vec{n} = (2; -3; 4)$
2. Tìm VTCP
QUY TRÌNH 3 BƯỚC:
Bước 1: Xác định dạng bài
- Có PTTS hoặc chính tắc? → Đọc trực tiếp
- Có 2 điểm? → Tính $\overrightarrow{AB}$
- Có phương trình tổng quát (mp)? → Từ VTPT
- Giao 2 mặt phẳng? → Tích có hướng VTPT
Bước 2: Tính toán
- PTTS/chính tắc: Đọc hệ số
- Hai điểm: $\vec{u} = (x_B-x_A; y_B-y_A; z_B-z_A)$
- Từ VTPT: $\vec{n}=(a;b)$ → $\vec{u}=(-b;a)$
- Giao tuyến: $\vec{u} = \vec{n_1} \times \vec{n_2}$
Bước 3: Kiểm tra
- $\vec{n} \cdot \vec{u} = 0$ (vuông góc với VTPT)
- Hoặc thay điểm vào phương trình
3. Mẹo nhớ
Cho VTPT:
“Vuông góc” → Dùng tích vô hướng kiểm tra: $\vec{n} \cdot \vec{v} = 0$
Cho VTCP:
“Song song” → Dùng tỷ lệ kiểm tra: $\frac{x_1}{x_2} = \frac{y_1}{y_2} = \frac{z_1}{z_2}$
Mặt phẳng → VTPT:
“Đọc hệ số $(A; B; C)$” từ $Ax + By + Cz + D = 0$
Đường thẳng → VTCP:
“Đọc mẫu số” từ phương trình chính tắc $\frac{x-x_0}{a} = \frac{y-y_0}{b} = \frac{z-z_0}{c}$
Từ VTPT tìm VTCP (mặt phẳng):
“Đổi chỗ và đổi dấu một số”: $(a; b)$ → $(-b; a)$
VII. BÀI TẬP MẪU
Bài 1: Tìm VTPT của mặt phẳng
Đề bài: Cho mặt phẳng $(P): 2x – 3y + z – 5 = 0$. Tìm một vectơ pháp tuyến của $(P)$.
Lời giải:
Từ phương trình tổng quát, đọc hệ số của $x$, $y$, $z$: $$\vec{n} = (2; -3; 1)$$
Đáp án: $\vec{n} = (2; -3; 1)$
Bài 2: Tìm VTPT qua 3 điểm
Đề bài: Tìm vectơ pháp tuyến của mặt phẳng đi qua ba điểm $A(1; 0; 0)$, $B(0; 2; 0)$, $C(0; 0; 3)$.
Lời giải:
Bước 1: Tính các vectơ
- $\overrightarrow{AB} = (0-1; 2-0; 0-0) = (-1; 2; 0)$
- $\overrightarrow{AC} = (0-1; 0-0; 3-0) = (-1; 0; 3)$
Bước 2: Tính tích có hướng $$\vec{n} = \overrightarrow{AB} \times \overrightarrow{AC} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ -1 & 2 & 0 \\ -1 & 0 & 3 \end{vmatrix}$$
$$= \vec{i}(6-0) – \vec{j}(-3-0) + \vec{k}(0-(-2))$$ $$= 6\vec{i} + 3\vec{j} + 2\vec{k}$$
Đáp án: $\vec{n} = (6; 3; 2)$ hoặc rút gọn không được vì đã tối giản
Bài 3: Tìm VTCP từ phương trình chính tắc
Đề bài: Đường thẳng $d$ có phương trình: $\frac{x-1}{2} = \frac{y+1}{-3} = \frac{z}{4}$. Tìm vectơ chỉ phương của $d$.
Lời giải:
Đọc mẫu số của phương trình chính tắc: $$\vec{u} = (2; -3; 4)$$
Đáp án: $\vec{u} = (2; -3; 4)$
Bài 4: Tìm VTCP từ VTPT
Đề bài: Đường thẳng $d$ trong mặt phẳng Oxy có phương trình: $3x – 4y + 5 = 0$. Tìm một vectơ chỉ phương của $d$.
Lời giải:
Bước 1: Tìm VTPT $$\vec{n} = (3; -4)$$
Bước 2: Từ VTPT, tìm VTCP bằng cách đổi chỗ và đổi dấu $$\vec{u} = (4; 3) \text{ hoặc } (-4; -3)$$
Kiểm tra: $\vec{n} \cdot \vec{u} = 3 \times 4 + (-4) \times 3 = 12 – 12 = 0$ ✓
Đáp án: $\vec{u} = (4; 3)$ hoặc $\vec{u} = (-4; -3)$
Bài 5: Tìm VTCP của giao tuyến hai mặt phẳng
Đề bài: Cho hai mặt phẳng:
- $(P_1): x + y + z = 0$
- $(P_2): x – y + 2z = 0$
Tìm vectơ chỉ phương của giao tuyến $d = (P_1) \cap (P_2)$.
Lời giải:
Bước 1: Xác định VTPT của mỗi mặt phẳng
- $\vec{n_1} = (1; 1; 1)$
- $\vec{n_2} = (1; -1; 2)$
Bước 2: VTCP của giao tuyến là tích có hướng hai VTPT $$\vec{u} = \vec{n_1} \times \vec{n_2} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 1 & 1 & 1 \\ 1 & -1 & 2 \end{vmatrix}$$
$$= \vec{i}(2-(-1)) – \vec{j}(2-1) + \vec{k}(-1-1)$$ $$= 3\vec{i} – \vec{j} – 2\vec{k}$$
Đáp án: $\vec{u} = (3; -1; -2)$
VIII. MẸO VÀ LƯU Ý
1. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm lẫn VTPT và VTCP
Nhớ:
- VTPT: Vuông góc (perpendicular)
- VTCP: Song song (direction)
❌ SAI LẦM 2: Quên đổi dấu khi tìm VTCP từ VTPT
Sai: $\vec{n} = (3; 4)$ → $\vec{u} = (4; 3)$ ❌
Đúng: $\vec{n} = (3; 4)$ → $\vec{u} = (-4; 3)$ hoặc $(4; -3)$ ✓
❌ SAI LẦM 3: Đọc sai hệ số từ phương trình
Sai: $2x – 3y + 5 = 0$ → $\vec{n} = (2; 3)$ ❌
Đúng: $2x – 3y + 5 = 0$ → $\vec{n} = (2; -3)$ ✓
Chú ý dấu âm!
❌ SAI LẦM 4: Quên rằng $k\vec{n}$ cũng là VTPT/VTCP
Nếu $\vec{n} = (2; 3; 4)$ là VTPT thì:
- $2\vec{n} = (4; 6; 8)$ cũng là VTPT ✓
- $-\vec{n} = (-2; -3; -4)$ cũng là VTPT ✓
2. Kiểm tra nhanh kết quả
Kiểm tra 1: VTPT ⊥ VTCP
$$\vec{n} \cdot \vec{u} = 0$$
Nếu tích vô hướng khác 0 → Sai!
Kiểm tra 2: Thay tọa độ điểm vào phương trình
Nếu điểm $M(x_0; y_0; z_0)$ thuộc mặt phẳng thì phải thỏa mãn phương trình.
Kiểm tra 3: Kiểm tra tỷ lệ nếu song song
Hai vectơ $\vec{u_1} = (a_1; b_1; c_1)$ và $\vec{u_2} = (a_2; b_2; c_2)$ cùng phương khi: $$\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}$$
IX. KẾT LUẬN
Tổng kết
Bài viết đã trình bày đầy đủ kiến thức về vectơ pháp tuyến và vectơ chỉ phương:
Vectơ pháp tuyến (VTPT):
- Vectơ vuông góc với đường thẳng/mặt phẳng
- Đọc hệ số từ phương trình tổng quát
- Hoặc dùng tích có hướng qua 3 điểm
Vectơ chỉ phương (VTCP):
- Vectơ song song với đường thẳng
- Đọc từ phương trình tham số/chính tắc
- Hoặc tính $\overrightarrow{AB}$ qua 2 điểm
Mối liên hệ:
- $\vec{n} \perp \vec{u}$ → $\vec{n} \cdot \vec{u} = 0$
- Chuyển đổi: $(a; b)$ → $(-b; a)$
Công thức quan trọng nhất
BA CÔNG THỨC CỐT LÕI:
Mặt phẳng: $$Ax + By + Cz + D = 0 \quad \Rightarrow \quad \vec{n} = (A; B; C)$$
Đường thẳng (chính tắc): $$\frac{x-x_0}{a} = \frac{y-y_0}{b} = \frac{z-z_0}{c} \quad \Rightarrow \quad \vec{u} = (a; b; c)$$
Qua 3 điểm: $$\vec{n} = \overrightarrow{AB} \times \overrightarrow{AC}$$
Tài liệu tham khảo
Các chủ đề liên quan:
- [Phương trình mặt phẳng trong không gian]
- [Phương trình đường thẳng – Tham số và chính tắc]
- [Tích có hướng của hai vectơ]
- [Vị trí tương đối giữa đường thẳng và mặt phẳng]
- [Góc giữa đường thẳng và mặt phẳng]

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
