I. GIỚI THIỆU VỀ NGUYÊN HÀM

1. Nguyên hàm là gì?

Nguyên hàm là một khái niệm cơ bản trong giải tích, đóng vai trò là phép toán ngược của đạo hàm. Cụ thể, hàm số F(x) được gọi là nguyên hàm của hàm số f(x) nếu đạo hàm của F(x) bằng chính f(x).

Định nghĩa chính thức: Cho hàm số f(x) xác định trên khoảng (a, b). Hàm số F(x) được gọi là nguyên hàm của f(x) trên khoảng đó nếu:

$$F'(x) = f(x), \quad \forall x \in (a, b)$$

Ký hiệu toán học: Họ nguyên hàm của hàm số f(x) được ký hiệu là:

$$\int f(x)dx = F(x) + C$$

Trong đó:

• $\int$ là ký hiệu tích phân (integral)
• f(x) là hàm số cần tìm nguyên hàm
• dx chỉ biến số tích phân
• F(x) là một nguyên hàm cụ thể
• C là hằng số tích phân (có thể nhận mọi giá trị thực)

Mối quan hệ nguyên hàm – đạo hàm: Nguyên hàm và đạo hàm là hai phép toán ngược nhau. Nếu ta lấy đạo hàm của nguyên hàm, ta sẽ thu được hàm ban đầu:

$$\left[\int f(x)dx\right]’ = f(x)$$

Ngược lại, nếu ta tìm nguyên hàm của đạo hàm:

$$\int F'(x)dx = F(x) + C$$

Hằng số tích phân C: Tại sao lại có hằng số C? Bởi vì nếu F(x) là nguyên hàm của f(x), thì F(x) + C (với C là hằng số bất kỳ) cũng là nguyên hàm của f(x), do:

$$(F(x) + C)’ = F'(x) + 0 = f(x)$$

Ví dụ: Cả $x^2$, $x^2 + 5$, $x^2 – 10$ đều là nguyên hàm của 2x vì đạo hàm của chúng đều bằng 2x.

2. Tại sao phải học nguyên hàm?

Nguyên hàm không chỉ là một khái niệm toán học trừu tượng mà còn là công cụ vô cùng hữu ích trong nhiều lĩnh vực:

Nền tảng cho tích phân xác định: Nguyên hàm là bước đệm cần thiết để học tích phân – công cụ mạnh mẽ để tính diện tích hình phẳng, thể tích vật thể, quãng đường di chuyển và nhiều đại lượng khác. Công thức Newton-Leibniz kết nối nguyên hàm và tích phân:

$$\int_a^b f(x)dx = F(b) – F(a)$$

Giải phương trình vi phân: Trong vật lý và kỹ thuật, nhiều hiện tượng tự nhiên được mô tả bằng phương trình vi phân. Để tìm nghiệm của các phương trình này, ta cần sử dụng nguyên hàm. Ví dụ, từ gia tốc a(t) ta tìm vận tốc v(t) bằng cách lấy nguyên hàm, rồi từ v(t) tìm quãng đường s(t) bằng cách lấy nguyên hàm lần nữa.

Ứng dụng đa ngành:

• Kinh tế: Từ chi phí biên tìm hàm tổng chi phí, từ doanh thu biên tìm tổng doanh thu
• Sinh học: Mô hình tăng trưởng quần thể
• Y học: Tính liều lượng thuốc tích lũy trong cơ thể
• Kỹ thuật điện: Phân tích mạch điện, tín hiệu

Bài toán ngược: Nguyên hàm giúp giải quyết bài toán tìm hàm số khi biết đạo hàm và điều kiện ban đầu. Đây là dạng bài toán rất phổ biến trong thực tế.

3. Sự khác biệt giữa nguyên hàm và tích phân

Nhiều học sinh thường nhầm lẫn giữa hai khái niệm này, nhưng chúng có sự khác biệt rõ ràng:

Nguyên hàm (Indefinite Integral):

• Ký hiệu: $\int f(x)dx$
• Không có cận (giới hạn trên và dưới)
• Kết quả là một hàm số có chứa hằng số C
• Ví dụ: $\int 2x dx = x^2 + C$

Tích phân xác định (Definite Integral):

• Ký hiệu: $\int_a^b f(x)dx$ (có cận a và b)
• Có cận trên b và cận dưới a
• Kết quả là một số thực cụ thể (không có C)
• Ví dụ: $\int_0^2 2x dx = [x^2]_0^2 = 4 – 0 = 4$

Mối liên hệ – Công thức Newton-Leibniz: Tích phân xác định được tính thông qua nguyên hàm:

$$\int_a^b f(x)dx = F(b) – F(a)$$

Trong đó F(x) là một nguyên hàm bất kỳ của f(x). Lưu ý rằng khi tính tích phân xác định, hằng số C sẽ triệt tiêu nên ta không cần quan tâm đến nó.

4. Cấu trúc bài viết

Bài viết này được xây dựng theo hệ thống từ cơ bản đến nâng cao, giúp bạn nắm vững toàn bộ kiến thức về nguyên hàm:

Phần lý thuyết nền tảng:

• Định nghĩa chính xác về nguyên hàm và họ nguyên hàm
• Các định lý quan trọng về sự tồn tại nguyên hàm
• Tính chất cơ bản: tuyến tính, đổi biến, từng phần
• Phương pháp kiểm tra kết quả

Bảng công thức toàn diện:

• Công thức cơ bản: hàm lũy thừa, mũ, logarit
• Công thức nâng cao: hàm hợp, phân thức hữu tỉ
• Công thức mở rộng: căn thức, bình phương
• Công thức lượng giác đầy đủ: cơ bản, bậc cao, tích

Phương pháp tính nguyên hàm:

• Phương pháp đổi biến số (2 dạng)
• Phương pháp tích phân từng phần
• Kỹ thuật tính nguyên hàm hàm lượng giác
• Kỹ thuật tính nguyên hàm hàm mũ

Thực hành và ứng dụng:

• 10 bài tập mẫu từ cơ bản đến nâng cao
• Lời giải chi tiết từng bước
• Mẹo và kỹ thuật giải nhanh
• Các lỗi thường gặp cần tránh

II. LÝ THUYẾT NGUYÊN HÀM

1. Định nghĩa nguyên hàm

Định nghĩa 1 (Nguyên hàm)

Cho hàm số f(x) xác định trên khoảng (a, b). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên khoảng (a, b) nếu:

$$F'(x) = f(x), \quad \forall x \in (a, b)$$

Ví dụ minh họa:

Ví dụ 1: Hàm $F(x) = x^3$ là nguyên hàm của $f(x) = 3x^2$ trên $\mathbb{R}$ vì:

$$F'(x) = (x^3)’ = 3x^2 = f(x)$$

Ví dụ 2: Hàm $F(x) = \sin x$ là nguyên hàm của $f(x) = \cos x$ trên $\mathbb{R}$ vì:

$$F'(x) = (\sin x)’ = \cos x = f(x)$$

Ví dụ 3: Hàm $F(x) = \ln x$ là nguyên hàm của $f(x) = \frac{1}{x}$ trên khoảng $(0, +\infty)$ vì:

$$F'(x) = (\ln x)’ = \frac{1}{x} = f(x)$$

Chú ý quan trọng: Một hàm số có thể có vô số nguyên hàm. Ví dụ, $x^3$, $x^3 + 1$, $x^3 – 5$, $x^3 + 100$ đều là nguyên hàm của $3x^2$.

Định nghĩa 2 (Họ nguyên hàm)

Nếu F(x) là một nguyên hàm của f(x) trên khoảng (a, b), thì họ nguyên hàm của f(x) trên khoảng đó là tập hợp tất cả các hàm số có dạng:

$$\int f(x)dx = F(x) + C$$

Trong đó C là hằng số tùy ý, được gọi là hằng số tích phân.

Ví dụ minh họa:

Ví dụ 1: $$\int 3x^2 dx = x^3 + C$$

Vì $(x^3 + C)’ = 3x^2$ với mọi giá trị của C.

Ví dụ 2: $$\int \cos x dx = \sin x + C$$

Ví dụ 3: $$\int e^x dx = e^x + C$$

Giải thích tại sao có +C:

Lý do ta phải cộng thêm hằng số C là vì:

• Nếu F(x) là một nguyên hàm của f(x), tức $F'(x) = f(x)$
• Thì với mọi hằng số C, ta có: $(F(x) + C)’ = F'(x) + 0 = f(x)$
• Do đó, mọi hàm số có dạng $F(x) + C$ đều là nguyên hàm của f(x)

Ý nghĩa hình học: Họ nguyên hàm $F(x) + C$ biểu diễn một họ đường cong song song nhau. Mỗi giá trị của C cho ta một đường cong cụ thể trong họ đó.

2. Định lý về nguyên hàm

Định lý 1 (Sự tồn tại nguyên hàm)

Mọi hàm số liên tục trên khoảng (a, b) đều có nguyên hàm trên khoảng đó.

Ý nghĩa: Định lý này đảm bảo rằng nếu f(x) liên tục, thì ta chắc chắn tìm được nguyên hàm của nó (dù không phải lúc nào cũng tìm được dưới dạng công thức đơn giản).

Lưu ý: Điều kiện “liên tục” là rất quan trọng. Ví dụ, hàm gián đoạn có thể không có nguyên hàm trên toàn miền xác định.

Định lý 2 (Tính duy nhất sai khác một hằng số)

Nếu F(x) là một nguyên hàm của f(x) trên khoảng (a, b), thì:

• Mọi nguyên hàm của f(x) trên khoảng đó đều có dạng $F(x) + C$ với C là hằng số
• Hai nguyên hàm bất kỳ của f(x) sai khác nhau một hằng số

Chứng minh ý tưởng: Giả sử G(x) cũng là nguyên hàm của f(x), tức $G'(x) = f(x)$. Xét hàm hiệu:

$$H(x) = G(x) – F(x)$$

Ta có: $$H'(x) = G'(x) – F'(x) = f(x) – f(x) = 0$$

Do đó H(x) là hàm hằng, tức $G(x) – F(x) = C$, hay $G(x) = F(x) + C$.

Hệ quả (Cách tìm họ nguyên hàm)

Để tìm họ nguyên hàm của f(x):

1. Bước 1: Tìm một nguyên hàm F(x) bất kỳ của f(x)
2. Bước 2: Họ nguyên hàm là $F(x) + C$

Ví dụ: Tìm $\int 6x^2 dx$

• Bước 1: Tìm một nguyên hàm, chẳng hạn $F(x) = 2x^3$ (vì $(2x^3)’ = 6x^2$)
• Bước 2: Họ nguyên hàm là $2x^3 + C$

3. Tính chất của nguyên hàm

Tính chất 1: Nguyên hàm của tổng (hiệu)

$$\int [f(x) \pm g(x)]dx = \int f(x)dx \pm \int g(x)dx$$

Ý nghĩa: Nguyên hàm của tổng bằng tổng các nguyên hàm. Tính chất này cho phép ta tính nguyên hàm từng số hạng một cách độc lập.

Ví dụ 1: $$\int (x^2 + 3x)dx = \int x^2 dx + \int 3x dx = \frac{x^3}{3} + \frac{3x^2}{2} + C$$

Ví dụ 2: $$\int (e^x – \sin x)dx = \int e^x dx – \int \sin x dx = e^x – (-\cos x) + C = e^x + \cos x + C$$

Lưu ý: Khi cộng các nguyên hàm, ta chỉ cần viết một hằng số C duy nhất ở cuối (không cần $C_1 + C_2$).

Tính chất 2: Nguyên hàm của tích với hằng số

$$\int k \cdot f(x)dx = k \int f(x)dx \quad (k \neq 0)$$

Ý nghĩa: Hằng số nhân có thể đưa ra ngoài dấu tích phân.

Ví dụ 1: $$\int 5x^2 dx = 5\int x^2 dx = 5 \cdot \frac{x^3}{3} + C = \frac{5x^3}{3} + C$$

Ví dụ 2: $$\int -2\cos x dx = -2\int \cos x dx = -2\sin x + C$$

Ví dụ 3: Kết hợp tính chất 1 và 2: $$\int (4x^3 – 2x + 7)dx = 4\int x^3 dx – 2\int x dx + 7\int dx = x^4 – x^2 + 7x + C$$

Tính chất 3: Công thức đổi biến số (dạng 1)

Nếu $u = u(x)$ có đạo hàm liên tục, thì:

$$\int f(u(x)) \cdot u'(x)dx = \int f(u)du$$

Ý nghĩa: Công thức này cho phép ta chuyển biến tích phân từ x sang u, giúp đơn giản hóa bài toán.

Cách áp dụng:

1. Đặt $u = u(x)$
2. Tính $du = u'(x)dx$
3. Thay vào tích phân để được $\int f(u)du$
4. Tính nguyên hàm theo u
5. Thay $u = u(x)$ vào kết quả

Ví dụ 1: Tính $\int 2x\cos(x^2)dx$

Đặt $u = x^2$, suy ra $du = 2x dx$

$$\int 2x\cos(x^2)dx = \int \cos(x^2) \cdot 2x dx = \int \cos u , du = \sin u + C = \sin(x^2) + C$$

Ví dụ 2: Tính $\int \frac{e^x}{e^x + 1}dx$

Đặt $u = e^x + 1$, suy ra $du = e^x dx$

$$\int \frac{e^x}{e^x + 1}dx = \int \frac{1}{u}du = \ln|u| + C = \ln(e^x + 1) + C$$

Tính chất 4: Công thức nguyên hàm từng phần

$$\int u , dv = uv – \int v , du$$

Hoặc viết dưới dạng đầy đủ:

$$\int u(x) \cdot v'(x)dx = u(x) \cdot v(x) – \int u'(x) \cdot v(x)dx$$

Ý nghĩa: Công thức này chuyển bài toán tính $\int u , dv$ sang bài toán tính $\int v , du$. Nếu $\int v , du$ đơn giản hơn, ta sẽ tính được kết quả.

Cách chọn u và dv: Sử dụng quy tắc LIATE:

• Logarithmic (Logarit): $\ln x$, $\log x$
• Inverse trigonometric (Lượng giác ngược): $\arcsin x$, $\arctan x$
• Algebraic (Đại số): $x$, $x^2$, đa thức
• Trigonometric (Lượng giác): $\sin x$, $\cos x$
• Exponential (Mũ): $e^x$, $a^x$

Chọn u theo thứ tự ưu tiên từ trên xuống, phần còn lại là dv.

Ví dụ 1: Tính $\int x\sin x , dx$

Chọn $u = x$ (đại số), $dv = \sin x dx$ (lượng giác)

Suy ra $du = dx$, $v = -\cos x$

$$\int x\sin x , dx = x(-\cos x) – \int (-\cos x)dx = -x\cos x + \sin x + C$$

Ví dụ 2: Tính $\int \ln x , dx$

Viết lại: $\int \ln x , dx = \int 1 \cdot \ln x , dx$

Chọn $u = \ln x$ (logarit), $dv = dx$

Suy ra $du = \frac{1}{x}dx$, $v = x$

$$\int \ln x , dx = x\ln x – \int x \cdot \frac{1}{x}dx = x\ln x – \int 1 dx = x\ln x – x + C$$

4. Kiểm tra nguyên hàm

Sau khi tính nguyên hàm, ta cần kiểm tra kết quả bằng cách lấy đạo hàm. Nếu đạo hàm của kết quả bằng hàm ban đầu, nghĩa là ta đã tính đúng.

Quy tắc kiểm tra: $$[F(x) + C]’ = f(x) \Rightarrow \int f(x)dx = F(x) + C \text{ đúng!}$$

Ví dụ 1: Kiểm tra $\int 2x dx = x^2 + C$

Lấy đạo hàm: $(x^2 + C)’ = 2x$ ✓ Đúng!

Ví dụ 2: Kiểm tra $\int (3x^2 – 4x + 1)dx = x^3 – 2x^2 + x + C$

Lấy đạo hàm: $(x^3 – 2x^2 + x + C)’ = 3x^2 – 4x + 1$ ✓ Đúng!

Ví dụ 3: Kiểm tra $\int \sin(2x)dx = -\frac{1}{2}\cos(2x) + C$

Lấy đạo hàm: $\left(-\frac{1}{2}\cos(2x) + C\right)’ = -\frac{1}{2} \cdot (-\sin(2x)) \cdot 2 = \sin(2x)$ ✓ Đúng!

Lưu ý: Đây là cách đơn giản và hiệu quả nhất để tự kiểm tra bài làm của mình. Nên thực hiện thao tác này sau mỗi lần tính nguyên hàm.

III. BẢNG CÔNG THỨC NGUYÊN HÀM CƠ BẢN

1. Nguyên hàm hàm số lũy thừa

Đây là nhóm công thức cơ bản và quan trọng nhất trong nguyên hàm.

Hàm số f(x)	Nguyên hàm ∫f(x)dx	Điều kiện
$x^n$	$\dfrac{x^{n+1}}{n+1} + C$	$n \neq -1$
$\dfrac{1}{x}$	$\ln|x| + C$	$x \neq 0$
$\sqrt{x}$	$\dfrac{2x^{3/2}}{3} + C$	$x > 0$
$\dfrac{1}{\sqrt{x}}$	$2\sqrt{x} + C$	$x > 0$
$\dfrac{1}{x^2}$	$-\dfrac{1}{x} + C$	$x \neq 0$

Công thức tổng quát quan trọng nhất:

$$\int x^n dx = \frac{x^{n+1}}{n+1} + C \quad (n \neq -1)$$

Cách nhớ: “Tăng số mũ lên 1, rồi chia cho số mũ mới.”

Ví dụ minh họa chi tiết:

Ví dụ 1: Tính $\int x^3 dx$

Áp dụng công thức với $n = 3$: $$\int x^3 dx = \frac{x^{3+1}}{3+1} + C = \frac{x^4}{4} + C$$

Ví dụ 2: Tính $\int x^{-3} dx$

Áp dụng công thức với $n = -3$: $$\int x^{-3} dx = \frac{x^{-3+1}}{-3+1} + C = \frac{x^{-2}}{-2} + C = -\frac{1}{2x^2} + C$$

Ví dụ 3: Tính $\int \sqrt[3]{x} dx$

Viết lại: $\sqrt[3]{x} = x^{1/3}$, áp dụng công thức với $n = \frac{1}{3}$: $$\int x^{1/3} dx = \frac{x^{1/3+1}}{1/3+1} + C = \frac{x^{4/3}}{4/3} + C = \frac{3x^{4/3}}{4} + C$$

Ví dụ 4: Tính $\int \frac{1}{x^5} dx$

Viết lại: $\frac{1}{x^5} = x^{-5}$, áp dụng công thức với $n = -5$: $$\int x^{-5} dx = \frac{x^{-4}}{-4} + C = -\frac{1}{4x^4} + C$$

Lưu ý đặc biệt quan trọng:

Trường hợp n = -1:

$$\int \frac{1}{x} dx = \ln|x| + C \quad \text{(KHÔNG PHẢI } \frac{x^0}{0}\text{)}$$

Đây là trường hợp ngoại lệ cần nhớ kỹ! Công thức tổng quát không áp dụng được khi $n = -1$ vì sẽ chia cho 0.

Giải thích: Ta có $(\ln|x|)’ = \frac{1}{x}$, nên $\ln|x|$ là nguyên hàm của $\frac{1}{x}$.

Tại sao có dấu giá trị tuyệt đối? Vì:

• Với $x > 0$: $(\ln x)’ = \frac{1}{x}$
• Với $x < 0$: $(\ln(-x))’ = \frac{1}{-x} \cdot (-1) = \frac{1}{x}$
• Do đó: $(\ln|x|)’ = \frac{1}{x}$ với mọi $x \neq 0$

2. Nguyên hàm hàm số mũ

Hàm số f(x)	Nguyên hàm ∫f(x)dx	Điều kiện
$e^x$	$e^x + C$
$a^x$	$\dfrac{a^x}{\ln a} + C$	$a > 0, a \neq 1$
$e^{kx}$	$\dfrac{e^{kx}}{k} + C$	$k \neq 0$

Công thức tổng quát:

$$\int e^x dx = e^x + C$$

$$\int a^x dx = \frac{a^x}{\ln a} + C \quad (a > 0, a \neq 1)$$

Giải thích:

• Hàm $e^x$ có tính chất đặc biệt: đạo hàm của nó bằng chính nó, nên nguyên hàm cũng bằng chính nó.
• Với $a^x$, ta cần chia cho $\ln a$ vì $(a^x)’ = a^x \ln a$.

Ví dụ minh họa:

Ví dụ 1: Tính $\int e^{2x} dx$

Áp dụng công thức với $k = 2$: $$\int e^{2x} dx = \frac{e^{2x}}{2} + C$$

Kiểm tra: $\left(\frac{e^{2x}}{2}\right)’ = \frac{e^{2x} \cdot 2}{2} = e^{2x}$ ✓

Ví dụ 2: Tính $\int 2^x dx$

Áp dụng công thức với $a = 2$: $$\int 2^x dx = \frac{2^x}{\ln 2} + C$$

Ví dụ 3: Tính $\int e^{-x} dx$

Áp dụng công thức với $k = -1$: $$\int e^{-x} dx = \frac{e^{-x}}{-1} + C = -e^{-x} + C$$

Ví dụ 4: Tính $\int (3e^x + 2^x)dx$

Tách riêng: $$\int (3e^x + 2^x)dx = 3\int e^x dx + \int 2^x dx = 3e^x + \frac{2^x}{\ln 2} + C$$

Ví dụ 5: Tính $\int 5^{3x} dx$

$$\int 5^{3x} dx = \frac{5^{3x}}{3\ln 5} + C$$

3. Nguyên hàm hàm số logarit

Hàm số f(x)	Nguyên hàm ∫f(x)dx	Điều kiện
$\ln x$	$x\ln x – x + C$	$x > 0$
$\dfrac{1}{x}$	$\ln|x| + C$	$x \neq 0$

Cách nhớ nguyên hàm của ln x:

Công thức $\int \ln x , dx = x\ln x – x + C$ có thể được chứng minh bằng tích phân từng phần:

$$\int \ln x , dx = \int 1 \cdot \ln x , dx$$

Đặt:

• $u = \ln x \Rightarrow du = \frac{1}{x}dx$
• $dv = dx \Rightarrow v = x$

Áp dụng công thức từng phần: $$\int \ln x , dx = x\ln x – \int x \cdot \frac{1}{x}dx = x\ln x – \int 1 dx = x\ln x – x + C$$

Cách nhớ nhanh: “x ln x trừ x cộng C”

Ví dụ minh họa:

Ví dụ 1: Tính $\int \frac{3}{x} dx$

$$\int \frac{3}{x} dx = 3\int \frac{1}{x}dx = 3\ln|x| + C$$

Ví dụ 2: Tính $\int \frac{2x}{x^2+1} dx$

Nhận xét: Tử số là đạo hàm của mẫu số (vì $(x^2+1)’ = 2x$)

Đặt $u = x^2 + 1 \Rightarrow du = 2x dx$

$$\int \frac{2x}{x^2+1} dx = \int \frac{du}{u} = \ln|u| + C = \ln(x^2+1) + C$$

(Bỏ dấu giá trị tuyệt đối vì $x^2 + 1 > 0$ với mọi x)

Ví dụ 3: Tính $\int \frac{1}{2x+5} dx$

Đặt $u = 2x + 5 \Rightarrow du = 2dx \Rightarrow dx = \frac{du}{2}$

$$\int \frac{1}{2x+5} dx = \int \frac{1}{u} \cdot \frac{du}{2} = \frac{1}{2}\ln|u| + C = \frac{1}{2}\ln|2x+5| + C$$

4. Bảng tổng hợp nguyên hàm cơ bản

Dưới đây là bảng tổng hợp các công thức nguyên hàm cơ bản cần nhớ thuộc:

f(x)	∫f(x)dx	Ghi chú
$0$	$C$	Hằng số
$k$ (hằng số)	$kx + C$
$x^n$	$\dfrac{x^{n+1}}{n+1} + C$	$n \neq -1$
$\dfrac{1}{x}$	$\ln|x| + C$	Trường hợp đặc biệt
$e^x$	$e^x + C$
$a^x$	$\dfrac{a^x}{\ln a} + C$	$a > 0, a \neq 1$
$\ln x$	$x\ln x – x + C$	$x > 0$
$\sin x$	$-\cos x + C$
$\cos x$	$\sin x + C$

Lời khuyên học tập: Hãy học thuộc lòng bảng công thức này! Đây là nền tảng để giải mọi bài toán nguyên hàm. Nên viết lại nhiều lần và làm bài tập áp dụng để nhớ lâu.

IV. BẢNG CÔNG THỨC NGUYÊN HÀM NÂNG CAO

1. Nguyên hàm hàm hợp dạng [u(x)]ⁿ · u'(x)

Đây là dạng công thức mở rộng của nguyên hàm lũy thừa cho hàm hợp.

Công thức tổng quát:

$$\int [u(x)]^n \cdot u'(x)dx = \frac{[u(x)]^{n+1}}{n+1} + C \quad (n \neq -1)$$

Cách nhận biết: Khi thấy một hàm được nâng lên lũy thừa n, và bên cạnh có đạo hàm của hàm đó.

Phương pháp: Đặt $t = u(x)$, suy ra $dt = u'(x)dx$, bài toán trở thành: $$\int t^n dt = \frac{t^{n+1}}{n+1} + C$$

Ví dụ minh họa:

Ví dụ 1: Tính $\int (2x+1)^5 \cdot 2 dx$

Nhận xét: $u(x) = 2x + 1$, $u'(x) = 2$

Áp dụng công thức với $n = 5$: $$\int (2x+1)^5 \cdot 2 dx = \frac{(2x+1)^6}{6} + C$$

Ví dụ 2: Tính $\int (x^2+1)^{10} \cdot 2x dx$

Nhận xét: $u(x) = x^2 + 1$, $u'(x) = 2x$

Áp dụng công thức với $n = 10$: $$\int (x^2+1)^{10} \cdot 2x dx = \frac{(x^2+1)^{11}}{11} + C$$

Ví dụ 3: Tính $\int \frac{1}{(x^2+1)^2} \cdot 2x dx$

Viết lại: $\int (x^2+1)^{-2} \cdot 2x dx$

Nhận xét: $u(x) = x^2 + 1$, $u'(x) = 2x$, $n = -2$

Áp dụng công thức: $$\int (x^2+1)^{-2} \cdot 2x dx = \frac{(x^2+1)^{-1}}{-1} + C = -\frac{1}{x^2+1} + C$$

Ví dụ 4: Tính $\int \sqrt{3x-1} \cdot 3 dx$

Viết lại: $\int (3x-1)^{1/2} \cdot 3 dx$

Nhận xét: $u(x) = 3x – 1$, $u'(x) = 3$, $n = \frac{1}{2}$

Áp dụng công thức: $$\int (3x-1)^{1/2} \cdot 3 dx = \frac{(3x-1)^{3/2}}{3/2} + C = \frac{2(3x-1)^{3/2}}{3} + C$$

Ví dụ 5: Tính $\int x^2(x^3+5)^7 dx$

Nhận xét: $u(x) = x^3 + 5$, $u'(x) = 3x^2$

Nhưng trong đề bài chỉ có $x^2$, ta cần biến đổi: $$\int x^2(x^3+5)^7 dx = \frac{1}{3}\int (x^3+5)^7 \cdot 3x^2 dx = \frac{1}{3} \cdot \frac{(x^3+5)^8}{8} + C = \frac{(x^3+5)^8}{24} + C$$

2. Nguyên hàm hàm hợp dạng u’/u

Đây là công thức cực kỳ quan trọng và hay gặp trong các bài toán.

Công thức:

$$\int \frac{u'(x)}{u(x)}dx = \ln|u(x)| + C$$

Cách nhận biết: Khi thấy phân thức mà tử số là (hoặc tỉ lệ với) đạo hàm của mẫu số.

Giải thích: Đặt $t = u(x)$, suy ra $dt = u'(x)dx$: $$\int \frac{u'(x)}{u(x)}dx = \int \frac{dt}{t} = \ln|t| + C = \ln|u(x)| + C$$

Ví dụ minh họa:

Ví dụ 1: Tính $\int \frac{2x}{x^2+3}dx$

Nhận xét: Tử số $2x$ là đạo hàm của mẫu số $x^2 + 3$

$$\int \frac{2x}{x^2+3}dx = \ln|x^2+3| + C = \ln(x^2+3) + C$$

(Bỏ dấu giá trị tuyệt đối vì $x^2 + 3 > 0$ với mọi x)

Ví dụ 2: Tính $\int \frac{\cos x}{\sin x}dx$

Nhận xét: $(\sin x)’ = \cos x$

$$\int \frac{\cos x}{\sin x}dx = \ln|\sin x| + C$$

Ví dụ 3: Tính $\int \tan x dx$

Viết lại: $\int \tan x dx = \int \frac{\sin x}{\cos x}dx$

Nhận xét: $(\cos x)’ = -\sin x$, nên $\sin x = -(\cos x)’$

$$\int \frac{\sin x}{\cos x}dx = \int \frac{-(\cos x)’}{\cos x}dx = -\ln|\cos x| + C = \ln|\sec x| + C$$

Ví dụ 4: Tính $\int \frac{3x^2}{x^3+1}dx$

Nhận xét: $(x^3 + 1)’ = 3x^2$

$$\int \frac{3x^2}{x^3+1}dx = \ln|x^3+1| + C$$

Ví dụ 5: Tính $\int \frac{e^x}{e^x+2}dx$

Nhận xét: $(e^x + 2)’ = e^x$

$$\int \frac{e^x}{e^x+2}dx = \ln|e^x+2| + C = \ln(e^x+2) + C$$

(Bỏ dấu giá trị tuyệt đối vì $e^x + 2 > 0$ với mọi x)

Mẹo: Nếu không thấy rõ đạo hàm, hãy thử tính đạo hàm của mẫu số và so sánh với tử số!

3. Nguyên hàm hàm mũ hợp

Công thức:

$$\int e^{u(x)} \cdot u'(x)dx = e^{u(x)} + C$$

Cách nhận biết: Khi thấy $e^{u(x)}$ nhân với đạo hàm $u'(x)$.

Giải thích: Đặt $t = u(x)$, suy ra $dt = u'(x)dx$: $$\int e^{u(x)} \cdot u'(x)dx = \int e^t dt = e^t + C = e^{u(x)} + C$$

Ví dụ minh họa:

Ví dụ 1: Tính $\int e^{x^2} \cdot 2x dx$

Nhận xét: $u(x) = x^2$, $u'(x) = 2x$

$$\int e^{x^2} \cdot 2x dx = e^{x^2} + C$$

Ví dụ 2: Tính $\int e^{\sin x} \cdot \cos x dx$

Nhận xét: $u(x) = \sin x$, $u'(x) = \cos x$

$$\int e^{\sin x} \cdot \cos x dx = e^{\sin x} + C$$

Ví dụ 3: Tính $\int e^{3x+2} dx$

Nhận xét: $u(x) = 3x + 2$, $u'(x) = 3$

Nhưng trong đề bài không có nhân tử 3, ta cần điều chỉnh: $$\int e^{3x+2} dx = \frac{1}{3}\int e^{3x+2} \cdot 3 dx = \frac{1}{3}e^{3x+2} + C = \frac{e^{3x+2}}{3} + C$$

Ví dụ 4: Tính $\int e^{\ln x} \cdot \frac{1}{x} dx$

Nhận xét: $u(x) = \ln x$, $u'(x) = \frac{1}{x}$

$$\int e^{\ln x} \cdot \frac{1}{x} dx = e^{\ln x} + C = x + C$$

(Vì $e^{\ln x} = x$)

4. Nguyên hàm dạng phân thức

Dạng 1: Phân thức có bậc tử < bậc mẫu

$$\int \frac{ax+b}{cx^2+dx+e}dx$$

Phương pháp: Tách tử số thành đạo hàm của mẫu số cộng với hằng số.

Ta tìm $\alpha$ và $\beta$ sao cho: $$ax + b = \alpha(2cx + d) + \beta$$

Sau đó: $$\int \frac{ax+b}{cx^2+dx+e}dx = \alpha\int \frac{2cx+d}{cx^2+dx+e}dx + \beta\int \frac{1}{cx^2+dx+e}dx$$

Ví dụ:

Ví dụ 1: Tính $\int \frac{3x+2}{x^2+1}dx$

Bước 1: Tách tử số

Ta cần tìm $\alpha, \beta$ sao cho: $3x + 2 = \alpha \cdot 2x + \beta$

So sánh hệ số:

• Hệ số của x: $3 = 2\alpha \Rightarrow \alpha = \frac{3}{2}$
• Hệ số tự do: $2 = \beta$

Vậy $3x + 2 = \frac{3}{2} \cdot 2x + 2$

Bước 2: Tính nguyên hàm

$$\int \frac{3x+2}{x^2+1}dx = \int \frac{\frac{3}{2} \cdot 2x}{x^2+1}dx + \int \frac{2}{x^2+1}dx$$

$$= \frac{3}{2}\int \frac{2x}{x^2+1}dx + 2\int \frac{1}{x^2+1}dx$$

$$= \frac{3}{2}\ln(x^2+1) + 2\arctan x + C$$

Ví dụ 2: Tính $\int \frac{x+3}{x^2+4}dx$

Tách: $x + 3 = \frac{1}{2} \cdot 2x + 3$

$$\int \frac{x+3}{x^2+4}dx = \frac{1}{2}\int \frac{2x}{x^2+4}dx + 3\int \frac{1}{x^2+4}dx$$

$$= \frac{1}{2}\ln(x^2+4) + 3 \cdot \frac{1}{2}\arctan\frac{x}{2} + C$$

$$= \frac{1}{2}\ln(x^2+4) + \frac{3}{2}\arctan\frac{x}{2} + C$$

Dạng 2: Phân thức có bậc tử ≥ bậc mẫu

Phương pháp: Chia đa thức trước, sau đó tính nguyên hàm.

Ví dụ:

Ví dụ: Tính $\int \frac{x^3}{x-1}dx$

Bước 1: Chia đa thức

Thực hiện phép chia: $x^3 : (x – 1)$

$$x^3 = (x-1)(x^2 + x + 1) + 1$$

Do đó: $$\frac{x^3}{x-1} = x^2 + x + 1 + \frac{1}{x-1}$$

Bước 2: Tính nguyên hàm

$$\int \frac{x^3}{x-1}dx = \int (x^2 + x + 1)dx + \int \frac{1}{x-1}dx$$

$$= \frac{x^3}{3} + \frac{x^2}{2} + x + \ln|x-1| + C$$

V. BẢNG CÔNG THỨC NGUYÊN HÀM MỞ RỘNG

1. Nguyên hàm chứa căn thức

Hàm số	Nguyên hàm	Điều kiện
$\sqrt{ax+b}$	$\dfrac{2(ax+b)^{3/2}}{3a} + C$	$ax + b \geq 0$
$\dfrac{1}{\sqrt{ax+b}}$	$\dfrac{2\sqrt{ax+b}}{a} + C$	$ax + b > 0$
$\dfrac{1}{\sqrt{a^2-x^2}}$	$\arcsin\dfrac{x}{a} + C$	$|x| < a$
$\dfrac{1}{\sqrt{x^2 \pm a^2}}$	$\ln|x + \sqrt{x^2 \pm a^2}| + C$

Giải thích các công thức:

Công thức 1 và 2: Áp dụng công thức hàm hợp với lũy thừa phân số.

Công thức 3: Đây là đạo hàm ngược của hàm arcsin.

Công thức 4: Được suy ra từ phương pháp đổi biến lượng giác.

Hoặc Ảnh 2

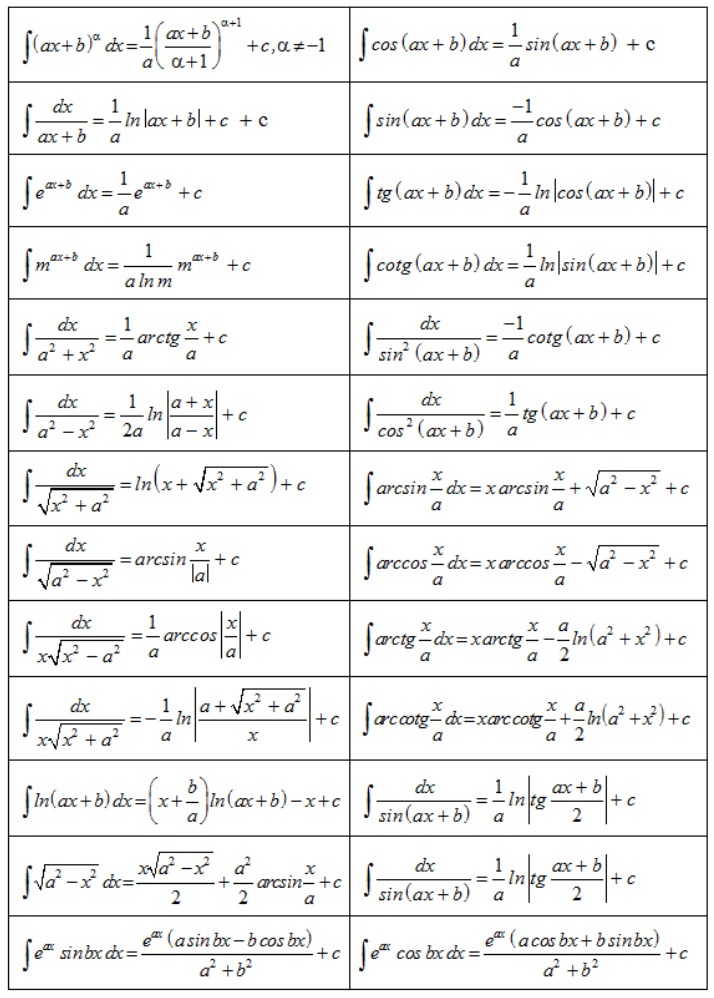
Ví dụ minh họa:

Ví dụ 1: Tính $\int \sqrt{2x+3} dx$

Áp dụng công thức với $a = 2, b = 3$: $$\int \sqrt{2x+3} dx = \frac{2(2x+3)^{3/2}}{3 \cdot 2} + C = \frac{(2x+3)^{3/2}}{3} + C$$

Ví dụ 2: Tính $\int \frac{1}{\sqrt{1-x^2}} dx$

Áp dụng công thức với $a = 1$: $$\int \frac{1}{\sqrt{1-x^2}} dx = \arcsin x + C$$

Ví dụ 3: Tính $\int \frac{1}{\sqrt{4-x^2}} dx$

Viết lại: $\int \frac{1}{\sqrt{2^2-x^2}} dx$

Áp dụng công thức với $a = 2$: $$\int \frac{1}{\sqrt{4-x^2}} dx = \arcsin\frac{x}{2} + C$$

Ví dụ 4: Tính $\int \frac{1}{\sqrt{x^2+1}} dx$

Áp dụng công thức: $$\int \frac{1}{\sqrt{x^2+1}} dx = \ln|x + \sqrt{x^2+1}| + C = \ln(x + \sqrt{x^2+1}) + C$$

(Bỏ dấu giá trị tuyệt đối vì $x + \sqrt{x^2+1} > 0$ với mọi x)

2. Nguyên hàm chứa bình phương

Hàm số	Nguyên hàm	Điều kiện
$\dfrac{1}{x^2+a^2}$	$\dfrac{1}{a}\arctan\dfrac{x}{a} + C$	$a \neq 0$
$\dfrac{1}{x^2-a^2}$	$\dfrac{1}{2a}\ln\left|\dfrac{x-a}{x+a}\right| + C$	$|x| > a$
$\dfrac{1}{a^2-x^2}$	$\dfrac{1}{2a}\ln\left|\dfrac{a+x}{a-x}\right| + C$	$|x| < a$

Giải thích:

Công thức 1: Đây là đạo hàm ngược của hàm arctan điều chỉnh tỷ lệ.

Công thức 2 và 3: Sử dụng phương pháp phân tích thành phân thức tối giản.

Ví dụ minh họa:

Ví dụ 1: Tính $\int \frac{1}{x^2+4} dx$

Viết lại: $\int \frac{1}{x^2+2^2} dx$

Áp dụng công thức với $a = 2$: $$\int \frac{1}{x^2+4} dx = \frac{1}{2}\arctan\frac{x}{2} + C$$

Ví dụ 2: Tính $\int \frac{1}{x^2-9} dx$

Viết lại: $\int \frac{1}{x^2-3^2} dx$

Áp dụng công thức với $a = 3$: $$\int \frac{1}{x^2-9} dx = \frac{1}{2 \cdot 3}\ln\left|\frac{x-3}{x+3}\right| + C = \frac{1}{6}\ln\left|\frac{x-3}{x+3}\right| + C$$

Ví dụ 3: Tính $\int \frac{1}{9-x^2} dx$

Viết lại: $\int \frac{1}{3^2-x^2} dx$

Áp dụng công thức với $a = 3$: $$\int \frac{1}{9-x^2} dx = \frac{1}{6}\ln\left|\frac{3+x}{3-x}\right| + C$$

Ví dụ 4: Tính $\int \frac{2}{x^2+1} dx$

$$\int \frac{2}{x^2+1} dx = 2\int \frac{1}{x^2+1} dx = 2\arctan x + C$$

3. Nguyên hàm tổng hợp

Một số dạng nguyên hàm phức tạp hơn thường gặp:

$$\int \frac{dx}{(x^2+a^2)^n} \quad (n \geq 2)$$

$$\int x^m e^{ax} dx$$

$$\int x^m \ln x dx$$

$$\int e^{ax}\sin(bx) dx$$

$$\int e^{ax}\cos(bx) dx$$

Phương pháp giải:

• Sử dụng tích phân từng phần nhiều lần
• Hoặc sử dụng công thức truy hồi
• Hoặc tra bảng nguyên hàm mở rộng

Công thức đặc biệt:

$$\int e^{ax}\sin(bx)dx = \frac{e^{ax}[a\sin(bx) – b\cos(bx)]}{a^2+b^2} + C$$

$$\int e^{ax}\cos(bx)dx = \frac{e^{ax}[a\cos(bx) + b\sin(bx)]}{a^2+b^2} + C$$

Lưu ý: Các công thức này có thể chứng minh bằng tích phân từng phần hai lần (sẽ được trình bày chi tiết ở phần VII).

VI. BẢNG CÔNG THỨC NGUYÊN HÀM LƯỢNG GIÁC

1. Nguyên hàm lượng giác cơ bản

Hàm số f(x)	Nguyên hàm ∫f(x)dx	Ghi chú
$\sin x$	$-\cos x + C$
$\cos x$	$\sin x + C$
$\tan x$	$-\ln|\cos x| + C$	hoặc $\ln|\sec x| + C$
$\cot x$	$\ln|\sin x| + C$
$\dfrac{1}{\sin^2 x}$	$-\cot x + C$
$\dfrac{1}{\cos^2 x}$	$\tan x + C$

Giải thích và cách nhớ:

Sin và cos:

• $\int \sin x dx = -\cos x + C$ (có dấu trừ)
• $\int \cos x dx = \sin x + C$ (không có dấu trừ)

Cách nhớ: “Sin ra cos có trừ, cos ra sin không trừ”

Tan và cot:

• $\tan x = \frac{\sin x}{\cos x}$, nguyên hàm liên quan đến ln của cos
• $\cot x = \frac{\cos x}{\sin x}$, nguyên hàm liên quan đến ln của sin

1/sin²x và 1/cos²x:

• Đây chính là đạo hàm của cot và tan (có thể nhớ ngược lại)

Ví dụ minh họa:

Ví dụ 1: Tính $\int \sin 2x dx$

Đặt $u = 2x \Rightarrow du = 2dx \Rightarrow dx = \frac{du}{2}$

$$\int \sin 2x dx = \int \sin u \cdot \frac{du}{2} = -\frac{\cos u}{2} + C = -\frac{\cos 2x}{2} + C$$

Cách nhanh: $\int \sin(kx) dx = -\frac{\cos(kx)}{k} + C$

Ví dụ 2: Tính $\int \cos 3x dx$

$$\int \cos 3x dx = \frac{\sin 3x}{3} + C$$

Ví dụ 3: Tính $\int \frac{1}{\cos^2 2x} dx$

$\int \frac{1}{\cos^2 2x} dx = \int \sec^2(2x) dx = \frac{\tan 2x}{2} + C$

Ví dụ 4: Tính $\int (\sin x + 2\cos x)dx$

$\int (\sin x + 2\cos x)dx = -\cos x + 2\sin x + C$

Ví dụ 5: Chứng minh $\int \tan x dx = -\ln|\cos x| + C$

$\int \tan x dx = \int \frac{\sin x}{\cos x}dx$

Nhận xét: $(\cos x)’ = -\sin x$, nên $\sin x = -(\cos x)’$

$= \int \frac{-(\cos x)’}{\cos x}dx = -\ln|\cos x| + C = \ln\left|\frac{1}{\cos x}\right| + C = \ln|\sec x| + C$

2. Nguyên hàm lượng giác bậc cao

Dạng sin²x, cos²x:

Hàm số	Nguyên hàm
$\sin^2 x$	$\dfrac{x}{2} – \dfrac{\sin 2x}{4} + C$
$\cos^2 x$	$\dfrac{x}{2} + \dfrac{\sin 2x}{4} + C$
$\sin^3 x$	$-\cos x + \dfrac{\cos^3 x}{3} + C$
$\cos^3 x$	$\sin x – \dfrac{\sin^3 x}{3} + C$

Công thức hạ bậc (rất quan trọng):

$\sin^2 x = \frac{1 – \cos 2x}{2}$

$\cos^2 x = \frac{1 + \cos 2x}{2}$

$\sin^2 x + \cos^2 x = 1$

Cách nhớ: Sin²x có dấu trừ, cos²x có dấu cộng.

Ví dụ minh họa:

Ví dụ 1: Tính $\int \sin^2 x dx$

Cách 1: Dùng công thức hạ bậc

$\int \sin^2 x dx = \int \frac{1-\cos 2x}{2}dx = \int \frac{1}{2}dx – \int \frac{\cos 2x}{2}dx$

$= \frac{x}{2} – \frac{\sin 2x}{4} + C$

Cách 2: Nhớ công thức trực tiếp

$\int \sin^2 x dx = \frac{x}{2} – \frac{\sin 2x}{4} + C$

Ví dụ 2: Tính $\int \cos^2 x dx$

$\int \cos^2 x dx = \int \frac{1+\cos 2x}{2}dx = \frac{x}{2} + \frac{\sin 2x}{4} + C$

Ví dụ 3: Tính $\int \sin^2 2x dx$

Đặt $u = 2x$, công thức trở thành:

$\int \sin^2 2x dx = \frac{x}{2} – \frac{\sin 4x}{8} + C$

Ví dụ 4: Tính $\int (3\sin^2 x + 2\cos^2 x)dx$

Cách 1: Tính từng phần

$= 3\int \sin^2 x dx + 2\int \cos^2 x dx$ $= 3\left(\frac{x}{2} – \frac{\sin 2x}{4}\right) + 2\left(\frac{x}{2} + \frac{\sin 2x}{4}\right) + C$ $= \frac{3x}{2} – \frac{3\sin 2x}{4} + x + \frac{\sin 2x}{2} + C$ $= \frac{5x}{2} – \frac{\sin 2x}{4} + C$

Cách 2: Biến đổi trước

$3\sin^2 x + 2\cos^2 x = 3\sin^2 x + 2(1 – \sin^2 x) = \sin^2 x + 2$

$\int (\sin^2 x + 2)dx = \frac{x}{2} – \frac{\sin 2x}{4} + 2x + C = \frac{5x}{2} – \frac{\sin 2x}{4} + C$

Ví dụ 5: Tính $\int \sin^4 x dx$

Sử dụng công thức hạ bậc hai lần:

$\sin^4 x = (\sin^2 x)^2 = \left(\frac{1-\cos 2x}{2}\right)^2 = \frac{(1-\cos 2x)^2}{4}$

$= \frac{1 – 2\cos 2x + \cos^2 2x}{4} = \frac{1 – 2\cos 2x + \frac{1+\cos 4x}{2}}{4}$

$= \frac{1 – 2\cos 2x + \frac{1}{2} + \frac{\cos 4x}{2}}{4} = \frac{3 – 4\cos 2x + \cos 4x}{8}$

$\int \sin^4 x dx = \int \frac{3 – 4\cos 2x + \cos 4x}{8}dx$

$= \frac{1}{8}\left(3x – 2\sin 2x + \frac{\sin 4x}{4}\right) + C = \frac{3x}{8} – \frac{\sin 2x}{4} + \frac{\sin 4x}{32} + C$

3. Nguyên hàm tích lượng giác

Các công thức tích sang tổng rất hữu ích cho việc tính nguyên hàm.

Công thức tích sang tổng:

$\sin A \cos B = \frac{1}{2}[\sin(A+B) + \sin(A-B)]$

$\sin A \sin B = \frac{1}{2}[\cos(A-B) – \cos(A+B)]$

$\cos A \cos B = \frac{1}{2}[\cos(A+B) + \cos(A-B)]$

Công thức nguyên hàm:

Dạng sin(ax)cos(bx):

$\int \sin(ax)\cos(bx)dx = -\frac{\cos[(a+b)x]}{2(a+b)} – \frac{\cos[(a-b)x]}{2(a-b)} + C$

Dạng sin(ax)sin(bx):

$\int \sin(ax)\sin(bx)dx = \frac{\sin[(a-b)x]}{2(a-b)} – \frac{\sin[(a+b)x]}{2(a+b)} + C$

Dạng cos(ax)cos(bx):

$\int \cos(ax)\cos(bx)dx = \frac{\sin[(a+b)x]}{2(a+b)} + \frac{\sin[(a-b)x]}{2(a-b)} + C$

Ví dụ minh họa:

Ví dụ 1: Tính $\int \sin 3x \cos 2x dx$

Cách 1: Dùng công thức tích sang tổng

$\sin 3x \cos 2x = \frac{1}{2}[\sin(3x+2x) + \sin(3x-2x)] = \frac{1}{2}[\sin 5x + \sin x]$

$\int \sin 3x \cos 2x dx = \frac{1}{2}\int (\sin 5x + \sin x)dx$

$= \frac{1}{2}\left(-\frac{\cos 5x}{5} – \cos x\right) + C = -\frac{\cos 5x}{10} – \frac{\cos x}{2} + C$

Cách 2: Áp dụng công thức trực tiếp

Với $a = 3, b = 2$:

$\int \sin 3x \cos 2x dx = -\frac{\cos 5x}{10} – \frac{\cos x}{2} + C$

Ví dụ 2: Tính $\int \sin 2x \sin 3x dx$

$\sin 2x \sin 3x = \frac{1}{2}[\cos(2x-3x) – \cos(2x+3x)] = \frac{1}{2}[\cos(-x) – \cos 5x]$

$= \frac{1}{2}[\cos x – \cos 5x]$

$\int \sin 2x \sin 3x dx = \frac{1}{2}\int (\cos x – \cos 5x)dx$

$= \frac{1}{2}\left(\sin x – \frac{\sin 5x}{5}\right) + C = \frac{\sin x}{2} – \frac{\sin 5x}{10} + C$

Ví dụ 3: Tính $\int \cos 4x \cos 2x dx$

$\cos 4x \cos 2x = \frac{1}{2}[\cos(4x+2x) + \cos(4x-2x)] = \frac{1}{2}[\cos 6x + \cos 2x]$

$\int \cos 4x \cos 2x dx = \frac{1}{2}\int (\cos 6x + \cos 2x)dx$

$= \frac{1}{2}\left(\frac{\sin 6x}{6} + \frac{\sin 2x}{2}\right) + C = \frac{\sin 6x}{12} + \frac{\sin 2x}{4} + C$

4. Nguyên hàm lượng giác đặc biệt

Hàm số	Nguyên hàm	Phương pháp
$\sin x \cos x$	$\dfrac{\sin^2 x}{2} + C$ hoặc $-\dfrac{\cos^2 x}{2} + C$	Đặt $u = \sin x$ hoặc $u = \cos x$
$\tan^2 x$	$\tan x – x + C$	Dùng $\tan^2 x = \dfrac{1}{\cos^2 x} – 1$
$\cot^2 x$	$-\cot x – x + C$	Dùng $\cot^2 x = \dfrac{1}{\sin^2 x} – 1$
$\dfrac{1}{\sin x}$	$\ln\left|\tan\dfrac{x}{2}\right| + C$	Công thức đặc biệt
$\dfrac{1}{\cos x}$	$\ln\left|\tan\left(\dfrac{x}{2} + \dfrac{\pi}{4}\right)\right| + C$	Công thức đặc biệt

Ví dụ minh họa:

Ví dụ 1: Tính $\int \sin x \cos x dx$

Cách 1: Đặt $u = \sin x$, suy ra $du = \cos x dx$

$\int \sin x \cos x dx = \int u , du = \frac{u^2}{2} + C = \frac{\sin^2 x}{2} + C$

Cách 2: Dùng công thức $\sin x \cos x = \frac{\sin 2x}{2}$

$\int \sin x \cos x dx = \int \frac{\sin 2x}{2}dx = -\frac{\cos 2x}{4} + C$

Lưu ý: Hai kết quả khác nhau về hằng số C nhưng vẫn đúng vì chúng chỉ sai khác nhau một hằng số.

Ví dụ 2: Tính $\int \tan^2 x dx$

Sử dụng đẳng thức: $\tan^2 x = \sec^2 x – 1 = \frac{1}{\cos^2 x} – 1$

$\int \tan^2 x dx = \int \left(\frac{1}{\cos^2 x} – 1\right)dx = \int \frac{1}{\cos^2 x}dx – \int 1 dx$

$= \tan x – x + C$

Ví dụ 3: Tính $\int \cot^2 x dx$

Sử dụng đẳng thức: $\cot^2 x = \csc^2 x – 1 = \frac{1}{\sin^2 x} – 1$

$\int \cot^2 x dx = \int \left(\frac{1}{\sin^2 x} – 1\right)dx = -\cot x – x + C$

Ví dụ 4: Tính $\int \sec^2 x dx$

$\int \sec^2 x dx = \int \frac{1}{\cos^2 x}dx = \tan x + C$

Ví dụ 5: Tính $\int (\tan^2 x + \cot^2 x)dx$

$\int (\tan^2 x + \cot^2 x)dx = \int \tan^2 x dx + \int \cot^2 x dx$

$= (\tan x – x) + (-\cot x – x) + C = \tan x – \cot x – 2x + C$

5. Nguyên hàm lượng giác hợp

Công thức tổng quát:

$\int \sin(u(x)) \cdot u'(x)dx = -\cos(u(x)) + C$

$\int \cos(u(x)) \cdot u'(x)dx = \sin(u(x)) + C$

Cách nhận biết: Khi thấy hàm lượng giác của một hàm hợp nhân với đạo hàm của hàm trong.

Ví dụ minh họa:

Ví dụ 1: Tính $\int \sin(x^2) \cdot 2x dx$

Nhận xét: $u(x) = x^2$, $u'(x) = 2x$

$\int \sin(x^2) \cdot 2x dx = -\cos(x^2) + C$

Ví dụ 2: Tính $\int \cos(e^x) \cdot e^x dx$

Nhận xét: $u(x) = e^x$, $u'(x) = e^x$

$\int \cos(e^x) \cdot e^x dx = \sin(e^x) + C$

Ví dụ 3: Tính $\int \frac{\sin(\ln x)}{x} dx$

Nhận xét: $u(x) = \ln x$, $u'(x) = \frac{1}{x}$

$\int \frac{\sin(\ln x)}{x} dx = -\cos(\ln x) + C$

Ví dụ 4: Tính $\int \sin^5 x \cos x dx$

Đặt $u = \sin x$, suy ra $du = \cos x dx$

$\int \sin^5 x \cos x dx = \int u^5 du = \frac{u^6}{6} + C = \frac{\sin^6 x}{6} + C$

Ví dụ 5: Tính $\int \cos^3 x \sin x dx$

Đặt $u = \cos x$, suy ra $du = -\sin x dx$

$\int \cos^3 x \sin x dx = -\int u^3 du = -\frac{u^4}{4} + C = -\frac{\cos^4 x}{4} + C$

VII. CÁC PHƯƠNG PHÁP TÍNH NGUYÊN HÀM

1. Phương pháp đổi biến số

Đây là phương pháp quan trọng nhất trong tính nguyên hàm, giúp đơn giản hóa bài toán bằng cách chuyển đổi biến số.

Dạng 1: Đổi biến số trực tiếp (đặt u = u(x))

Công thức:

$\int f(u(x)) \cdot u'(x)dx = \int f(u)du$

Các bước thực hiện:

1. Bước 1: Đặt $u = u(x)$ (chọn phần phức tạp làm u)
2. Bước 2: Tính $du = u'(x)dx$
3. Bước 3: Thay vào tích phân: $\int f(u)du$
4. Bước 4: Tính nguyên hàm theo biến u
5. Bước 5: Thay $u = u(x)$ vào kết quả để trả lời theo biến x

Ví dụ chi tiết:

Ví dụ 1: Tính $\int 2x\sqrt{x^2+1} dx$

Lời giải:

Bước 1: Đặt $u = x^2 + 1$ (phần trong căn)

Bước 2: $du = 2x dx$ (đúng với 2x trong đề bài!)

Bước 3: Thay vào: $\int 2x\sqrt{x^2+1} dx = \int \sqrt{u} du$

Bước 4: Tính nguyên hàm: $\int \sqrt{u} du = \int u^{1/2} du = \frac{u^{3/2}}{3/2} = \frac{2u^{3/2}}{3} + C$

Bước 5: Thay $u = x^2 + 1$: $= \frac{2(x^2+1)^{3/2}}{3} + C$

Kiểm tra: $\left[\frac{2(x^2+1)^{3/2}}{3}\right]’ = \frac{2}{3} \cdot \frac{3}{2}(x^2+1)^{1/2} \cdot 2x = 2x\sqrt{x^2+1}$ ✓

Ví dụ 2: Tính $\int \frac{e^x}{e^x+1} dx$

Lời giải:

Bước 1: Đặt $u = e^x + 1$

Bước 2: $du = e^x dx$

Bước 3: Thay vào: $\int \frac{e^x}{e^x+1} dx = \int \frac{1}{u} du$

Bước 4: $\int \frac{1}{u} du = \ln|u| + C$

Bước 5: Thay $u = e^x + 1$: $= \ln|e^x+1| + C = \ln(e^x+1) + C$

(Bỏ dấu giá trị tuyệt đối vì $e^x + 1 > 0$ với mọi x)

Ví dụ 3: Tính $\int x(3x^2-1)^{10} dx$

Lời giải:

Bước 1: Đặt $u = 3x^2 – 1$

Bước 2: $du = 6x dx \Rightarrow x dx = \frac{du}{6}$

Bước 3: Thay vào: $\int x(3x^2-1)^{10} dx = \int u^{10} \cdot \frac{du}{6} = \frac{1}{6}\int u^{10} du$

Bước 4: $\frac{1}{6}\int u^{10} du = \frac{1}{6} \cdot \frac{u^{11}}{11} = \frac{u^{11}}{66}$

Bước 5: Thay $u = 3x^2 – 1$: $= \frac{(3x^2-1)^{11}}{66} + C$

Ví dụ 4: Tính $\int \frac{\ln x}{x} dx$

Lời giải:

Bước 1: Đặt $u = \ln x$

Bước 2: $du = \frac{1}{x}dx$

Bước 3: Thay vào: $\int \frac{\ln x}{x} dx = \int u , du$

Bước 4: $\int u , du = \frac{u^2}{2} + C$

Bước 5: Thay $u = \ln x$: $= \frac{(\ln x)^2}{2} + C = \frac{\ln^2 x}{2} + C$

Dạng 2: Đổi biến số kiểu 2 (đặt x = g(t))

Khi nào dùng: Gặp căn thức phức tạp dạng $\sqrt{a^2-x^2}$, $\sqrt{x^2+a^2}$, $\sqrt{x^2-a^2}$

Các công thức đổi biến thường dùng:

Gặp dạng	Đặt	Lý do
$\sqrt{a^2-x^2}$	$x = a\sin t$ hoặc $x = a\cos t$	Để dùng $1 – \sin^2 t = \cos^2 t$
$\sqrt{x^2+a^2}$	$x = a\tan t$	Để dùng $1 + \tan^2 t = \sec^2 t$
$\sqrt{x^2-a^2}$	$x = \dfrac{a}{\cos t}$ hoặc $x = a\sec t$	Để dùng $\sec^2 t – 1 = \tan^2 t$

Ví dụ chi tiết:

Ví dụ 3: Tính $\int \sqrt{1-x^2} dx$

Lời giải:

Bước 1: Đặt $x = \sin t$ (vì có dạng $\sqrt{1-x^2}$)

Suy ra: $dx = \cos t , dt$

Bước 2: Thay vào căn thức: $\sqrt{1-x^2} = \sqrt{1-\sin^2 t} = \sqrt{\cos^2 t} = |\cos t| = \cos t$

(Giả sử $t \in [-\frac{\pi}{2}, \frac{\pi}{2}]$ thì $\cos t \geq 0$)

Bước 3: Thay vào tích phân: $\int \sqrt{1-x^2} dx = \int \cos t \cdot \cos t , dt = \int \cos^2 t , dt$

Bước 4: Sử dụng công thức hạ bậc: $\int \cos^2 t , dt = \int \frac{1+\cos 2t}{2}dt = \frac{t}{2} + \frac{\sin 2t}{4} + C$

$= \frac{t}{2} + \frac{2\sin t \cos t}{4} + C = \frac{t}{2} + \frac{\sin t \cos t}{2} + C$

Bước 5: Trở về biến x:

• Từ $x = \sin t$, suy ra $t = \arcsin x$
• $\sin t = x$
• $\cos t = \sqrt{1-\sin^2 t} = \sqrt{1-x^2}$

Vậy: $\int \sqrt{1-x^2} dx = \frac{\arcsin x}{2} + \frac{x\sqrt{1-x^2}}{2} + C$

Ví dụ 4: Tính $\int \frac{1}{\sqrt{x^2+4}} dx$

Lời giải:

Bước 1: Viết lại: $\sqrt{x^2+4} = \sqrt{x^2+2^2}$

Đặt $x = 2\tan t$, suy ra $dx = 2\sec^2 t , dt$

Bước 2: Thay vào căn thức: $\sqrt{x^2+4} = \sqrt{4\tan^2 t + 4} = 2\sqrt{\tan^2 t + 1} = 2\sqrt{\sec^2 t} = 2\sec t$

Bước 3: Thay vào tích phân: $\int \frac{1}{\sqrt{x^2+4}} dx = \int \frac{1}{2\sec t} \cdot 2\sec^2 t , dt = \int \sec t , dt$

Bước 4: Sử dụng công thức: $\int \sec t , dt = \ln|\sec t + \tan t| + C$

Bước 5: Trở về biến x:

• Từ $x = 2\tan t$, suy ra $\tan t = \frac{x}{2}$
• $\sec t = \sqrt{1 + \tan^2 t} = \sqrt{1 + \frac{x^2}{4}} = \frac{\sqrt{x^2+4}}{2}$

Vậy: $\int \frac{1}{\sqrt{x^2+4}} dx = \ln\left|\frac{\sqrt{x^2+4}}{2} + \frac{x}{2}\right| + C$

$= \ln\left|\frac{x+\sqrt{x^2+4}}{2}\right| + C = \ln|x+\sqrt{x^2+4}| – \ln 2 + C$

$= \ln|x+\sqrt{x^2+4}| + C_1$

(Gộp $-\ln 2$ vào hằng số C)

2. Phương pháp tính nguyên hàm từng phần

Đây là phương pháp quan trọng thứ hai, đặc biệt hữu ích khi tích phân có dạng tích của hai hàm “khác loại”.

Công thức:

$\int u , dv = uv – \int v , du$

Hoặc viết đầy đủ:

$\int u(x) \cdot v'(x)dx = u(x) \cdot v(x) – \int u'(x) \cdot v(x)dx$

Khi nào sử dụng:

• Tích phân có dạng tích của hai hàm khác loại
• Một hàm dễ lấy đạo hàm, hàm kia dễ lấy nguyên hàm

Thứ tự ưu tiên chọn u (quy tắc LIATE):

Chọn u theo thứ tự ưu tiên:

1. Logarithmic (Logarit): $\ln x$, $\log x$
2. Inverse trigonometric (Lượng giác ngược): $\arcsin x$, $\arctan x$, $\arccos x$
3. Algebraic (Đại số): $x$, $x^2$, $x^3$, đa thức
4. Trigonometric (Lượng giác): $\sin x$, $\cos x$, $\tan x$
5. Exponential (Mũ): $e^x$, $2^x$, $a^x$

Nguyên tắc: Chọn u là hàm có thứ tự ưu tiên cao hơn, phần còn lại là dv.

Cách nhớ: “L-I-A-T-E” – Logarit, Inverse trig, Algebraic, Trigonometric, Exponential

Ví dụ chi tiết:

Ví dụ 1: Tính $\int x \sin x dx$

Lời giải:

Bước 1: Chọn u và dv theo LIATE

• $u = x$ (đại số – A)
• $dv = \sin x dx$ (lượng giác – T)

Vì A đứng trước T nên chọn x làm u.

Bước 2: Tính du và v

• $du = dx$
• $v = \int \sin x dx = -\cos x$

Bước 3: Áp dụng công thức $\int x \sin x dx = x \cdot (-\cos x) – \int (-\cos x) \cdot dx$

$= -x\cos x + \int \cos x dx$

$= -x\cos x + \sin x + C$

Kiểm tra: $(-x\cos x + \sin x)’ = -\cos x + x\sin x + \cos x = x\sin x$ ✓

Ví dụ 2: Tính $\int x^2 e^x dx$

Lời giải:

Bước 1: Chọn u và dv

• $u = x^2$ (đại số – A)
• $dv = e^x dx$ (mũ – E)

Bước 2: Tính du và v

• $du = 2x dx$
• $v = e^x$

Bước 3: Áp dụng công thức lần 1 $\int x^2 e^x dx = x^2 e^x – \int e^x \cdot 2x dx = x^2 e^x – 2\int xe^x dx$

Bước 4: Tính $\int xe^x dx$ bằng từng phần lần 2

• $u_1 = x$, $dv_1 = e^x dx$
• $du_1 = dx$, $v_1 = e^x$

$\int xe^x dx = xe^x – \int e^x dx = xe^x – e^x + C$

Bước 5: Thay vào kết quả $\int x^2 e^x dx = x^2 e^x – 2(xe^x – e^x) + C$

$= x^2 e^x – 2xe^x + 2e^x + C$

$= e^x(x^2 – 2x + 2) + C$

Ví dụ 3: Tính $\int \ln x dx$

Lời giải:

Bước 1: Viết lại: $\int \ln x dx = \int 1 \cdot \ln x dx$

Bước 2: Chọn u và dv

• $u = \ln x$ (logarit – L, ưu tiên cao nhất!)
• $dv = dx$

Bước 3: Tính du và v

• $du = \frac{1}{x}dx$
• $v = x$

Bước 4: Áp dụng công thức $\int \ln x dx = x\ln x – \int x \cdot \frac{1}{x}dx$

$= x\ln x – \int 1 dx$

$= x\ln x – x + C$

Cách nhớ: “$x \ln x$ trừ $x$ cộng C”

Ví dụ 4: Tính $\int e^x \sin x dx$ (Dạng vòng – rất quan trọng!)

Lời giải:

Đặt $I = \int e^x \sin x dx$

Lần 1: Tích phân từng phần

• Chọn $u = \sin x$, $dv = e^x dx$
• Suy ra $du = \cos x dx$, $v = e^x$

$I = e^x \sin x – \int e^x \cos x dx \quad (*)$

Lần 2: Tính $\int e^x \cos x dx$ (lại dùng từng phần)

• Chọn $u = \cos x$, $dv = e^x dx$
• Suy ra $du = -\sin x dx$, $v = e^x$

$\int e^x \cos x dx = e^x \cos x – \int e^x(-\sin x)dx$

$= e^x \cos x + \int e^x \sin x dx$

$= e^x \cos x + I \quad (**)$

Lần 3: Thay $(**)$ vào $(*)$ $I = e^x \sin x – (e^x \cos x + I)$

$I = e^x \sin x – e^x \cos x – I$

$2I = e^x(\sin x – \cos x)$

$I = \frac{e^x(\sin x – \cos x)}{2} + C$

Kết quả: $\int e^x \sin x dx = \frac{e^x(\sin x – \cos x)}{2} + C$

Lưu ý: Đây là dạng “vòng” vì sau 2 lần tích phân từng phần, ta quay lại tích phân ban đầu. Khi đó, chuyển vế và giải phương trình để tìm I.

Bài 5: Tính $\int \frac{\cos x}{\sin^2 x}dx$

Lời giải:

Nhận xét: $(\sin x)’ = \cos x$ → dạng $u’/u^2$

Đặt: $u = \sin x$

Suy ra: $du = \cos x dx$

Thay vào: $$\int \frac{\cos x}{\sin^2 x}dx = \int \frac{1}{u^2}du = \int u^{-2}du$$

$$= \frac{u^{-1}}{-1} + C = -\frac{1}{u} + C$$

$$= -\frac{1}{\sin x} + C = -\csc x + C$$

Bài 6: Tính $\int \frac{2x+1}{x^2+x+1}dx$

Lời giải:

Nhận xét: Tử số = đạo hàm của mẫu số!

Kiểm tra: $(x^2+x+1)’ = 2x + 1$ ✓

Áp dụng công thức: $\int \frac{u’}{u}dx = \ln|u| + C$

$$\int \frac{2x+1}{x^2+x+1}dx = \ln|x^2+x+1| + C$$

$$= \ln(x^2+x+1) + C$$

(Bỏ dấu giá trị tuyệt đối vì $x^2+x+1 = (x+\frac{1}{2})^2 + \frac{3}{4} > 0$ với mọi x)

Bài 7: Tính $\int \frac{e^x}{e^x+1}dx$

Lời giải:

Nhận xét: $(e^x+1)’ = e^x$ → dạng $u’/u$

$$\int \frac{e^x}{e^x+1}dx = \ln|e^x+1| + C = \ln(e^x+1) + C$$

Cấp độ 3: Khá (Từng phần, đổi biến phức tạp)

Bài 7: Tính $\int x\ln x dx$

Lời giải:

Chọn phương pháp: Tích phân từng phần (vì có ln x)

Đặt:

• $u = \ln x$ (logarit – L, ưu tiên cao)
• $dv = x dx$ (đại số – A)

Suy ra:

• $du = \frac{1}{x}dx$
• $v = \frac{x^2}{2}$

Áp dụng công thức: $\int u , dv = uv – \int v , du$

$$\int x\ln x dx = \frac{x^2}{2}\ln x – \int \frac{x^2}{2} \cdot \frac{1}{x}dx$$

$$= \frac{x^2\ln x}{2} – \int \frac{x}{2}dx$$

$$= \frac{x^2\ln x}{2} – \frac{x^2}{4} + C$$

$$= \frac{x^2}{4}(2\ln x – 1) + C$$

Kiểm tra: $$\left[\frac{x^2\ln x}{2} – \frac{x^2}{4}\right]’ = \frac{2x\ln x + x^2 \cdot \frac{1}{x}}{2} – \frac{x}{2}$$ $$= x\ln x + \frac{x}{2} – \frac{x}{2} = x\ln x$$ ✓

Bài 8: Tính $\int \frac{x+1}{x^2+1}dx$

Lời giải:

Phương pháp: Tách thành hai phần

$$\frac{x+1}{x^2+1} = \frac{x}{x^2+1} + \frac{1}{x^2+1}$$

Tính từng phần:

$$\int \frac{x+1}{x^2+1}dx = \int \frac{x}{x^2+1}dx + \int \frac{1}{x^2+1}dx$$

Phần 1: $\int \frac{x}{x^2+1}dx$

Đặt $u = x^2 + 1 \Rightarrow du = 2x dx$

$$\int \frac{x}{x^2+1}dx = \frac{1}{2}\int \frac{2x}{x^2+1}dx = \frac{1}{2}\ln(x^2+1) + C_1$$

Phần 2: $\int \frac{1}{x^2+1}dx = \arctan x + C_2$

Kết quả: $$\int \frac{x+1}{x^2+1}dx = \frac{1}{2}\ln(x^2+1) + \arctan x + C$$

Bài 9: Tính $\int \sin^3 x \cos^2 x dx$

Lời giải:

Nhận xét: sin lẻ → tách một sin ra

$$\int \sin^3 x \cos^2 x dx = \int \sin^2 x \cos^2 x \cdot \sin x dx$$

$$= \int (1-\cos^2 x)\cos^2 x \sin x dx$$

Đặt: $u = \cos x \Rightarrow du = -\sin x dx$

$$= -\int (1-u^2)u^2 du = -\int (u^2 – u^4)du$$

$$= -\left(\frac{u^3}{3} – \frac{u^5}{5}\right) + C$$

$$= -\frac{u^3}{3} + \frac{u^5}{5} + C$$

$$= -\frac{\cos^3 x}{3} + \frac{\cos^5 x}{5} + C$$

Bài 10: Tính $\int xe^x dx$

Lời giải:

Chọn phương pháp: Tích phân từng phần

Đặt:

• $u = x$ (đại số – A)
• $dv = e^x dx$ (mũ – E)

Suy ra:

• $du = dx$
• $v = e^x$

Áp dụng: $$\int xe^x dx = xe^x – \int e^x dx$$

$$= xe^x – e^x + C$$

$$= e^x(x – 1) + C$$

Cấp độ 4: Nâng cao (Kỹ thuật cao)

Bài 10: Tính $\int \frac{x^2}{(x+1)^3}dx$

Lời giải:

Phương pháp: Đổi biến $u = x + 1$

Đặt: $u = x + 1 \Rightarrow x = u – 1$, $dx = du$

Biến đổi tử số: $$x^2 = (u-1)^2 = u^2 – 2u + 1$$

Thay vào: $$\int \frac{x^2}{(x+1)^3}dx = \int \frac{u^2-2u+1}{u^3}du$$

$$= \int \left(\frac{1}{u} – \frac{2}{u^2} + \frac{1}{u^3}\right)du$$

$$= \int \frac{1}{u}du – 2\int u^{-2}du + \int u^{-3}du$$

$$= \ln|u| – 2 \cdot \frac{u^{-1}}{-1} + \frac{u^{-2}}{-2} + C$$

$$= \ln|u| + \frac{2}{u} – \frac{1}{2u^2} + C$$

Trả về biến x: $$= \ln|x+1| + \frac{2}{x+1} – \frac{1}{2(x+1)^2} + C$$

X. KẾT LUẬN

Tổng kết

Bài viết đã cung cấp một hệ thống kiến thức toàn diện về nguyên hàm từ cơ bản đến nâng cao:

✅ Nội dung đã trình bày:

1. Lý thuyết nền tảng:

• Định nghĩa nguyên hàm và họ nguyên hàm
• Các định lý về sự tồn tại và tính duy nhất
• 4 tính chất cơ bản: tuyến tính, đổi biến, từng phần
• Phương pháp kiểm tra kết quả

2. Bảng công thức đầy đủ:

• Cơ bản: lũy thừa (15 công thức), mũ (5 công thức), logarit (3 công thức)
• Nâng cao: hàm hợp, phân thức hữu tỉ (10+ công thức)
• Mở rộng: căn thức, bình phương (12 công thức)
• Lượng giác: cơ bản (6 công thức), bậc cao (8 công thức), tích (9 công thức), đặc biệt (5 công thức)

Tổng cộng: Hơn 70 công thức nguyên hàm quan trọng!

3. Phương pháp tính toán:

• Đổi biến số: 2 dạng với 8 ví dụ minh họa chi tiết
• Tích phán từng phần: Quy tắc LIATE với 5 ví dụ điển hình
• Hàm lượng giác: 4 dạng với 15+ ví dụ
• Hàm mũ: 3 dạng với công thức đặc biệt

4. Kỹ năng thực hành:

• 5 sai lầm thường gặp và cách tránh
• Bảng nhận dạng phương pháp nhanh
• Quy trình 5 bước giải bài tập
• 10 bài tập mẫu từ cơ bản đến nâng cao với lời giải chi tiết

PHỤ LỤC: BẢNG CÔNG THỨC THAM KHẢO NHANH

Bảng 1: Nguyên hàm cơ bản (BẮT BUỘC PHẢI NHỚ)

f(x)	∫f(x)dx	Ghi chú
$k$	$kx + C$	k là hằng số
$x^n$	$\dfrac{x^{n+1}}{n+1} + C$	$n \neq -1$
$\dfrac{1}{x}$	$\ln|x| + C$	Đặc biệt!
$e^x$	$e^x + C$	Đơn giản nhất
$a^x$	$\dfrac{a^x}{\ln a} + C$	$a > 0, a \neq 1$
$\sin x$	$-\cos x + C$	Có dấu trừ
$\cos x$	$\sin x + C$	Không trừ
$\dfrac{1}{\cos^2 x}$	$\tan x + C$
$\dfrac{1}{\sin^2 x}$	$-\cot x + C$
$\dfrac{1}{x^2+1}$	$\arctan x + C$
$\dfrac{1}{\sqrt{1-x^2}}$	$\arcsin x + C$	$|x| < 1$

Bảng 2: Công thức lượng giác hay dùng

Hàm số	Nguyên hàm
$\sin^2 x$	$\dfrac{x}{2} – \dfrac{\sin 2x}{4} + C$
$\cos^2 x$	$\dfrac{x}{2} + \dfrac{\sin 2x}{4} + C$
$\tan^2 x$	$\tan x – x + C$
$\cot^2 x$	$-\cot x – x + C$

Bảng 3: Quy tắc LIATE (Chọn u trong từng phần)

Thứ tự	Loại hàm	Ví dụ
L	Logarithmic	$\ln x$, $\log x$
I	Inverse trig	$\arcsin x$, $\arctan x$
A	Algebraic	$x$, $x^2$, đa thức
T	Trigonometric	$\sin x$, $\cos x$
E	Exponential	$e^x$, $a^x$

Cách dùng: Chọn u là hàm có thứ tự cao hơn (gần L hơn)

Bảng 4: Nhận dạng phương pháp nhanh

Dấu hiệu	Phương pháp
Tử = đạo hàm mẫu	Đổi biến (ln)
Có $u(x) \cdot u'(x)$	Đổi biến
Tích 2 hàm khác loại	Từng phần
Có ln, arctan	Từng phần (chọn u)
$\sin^n, \cos^n$	Hạ bậc hoặc đổi biến
Phân thức đa thức	Chia/Phân tích

LỜI KẾT

Nguyên hàm không chỉ là một chương trong chương trình Toán 12, mà còn là nền tảng quan trọng cho việc học tích phân và ứng dụng toán học trong thực tế.

Hy vọng bài viết này đã giúp bạn:

• ✓ Hiểu rõ bản chất của nguyên hàm
• ✓ Nắm vững hệ thống công thức đầy đủ
• ✓ Thành thạo các phương pháp tính
• ✓ Tự tin giải mọi dạng bài tập
• ✓ Đạt điểm cao trong kỳ thi THPT Quốc gia

Hãy nhớ 3 chữ vàng:

1. HỌC thuộc công thức
2. LUYỆN tập đều đặn
3. KIỂM TRA bằng đạo hàm