Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. Giới Thiệu Và Kiến Thức Cơ Bản
- 1. Định nghĩa đường tròn
- 2. Hệ tọa độ Oxy
- II. Phương Trình Đường Tròn Dạng Chuẩn
- 1. Công thức chuẩn
- 2. Các trường hợp đặc biệt
- 3. Cách viết phương trình
- 4. Ví dụ minh họa
- III. Phương Trình Đường Tròn Dạng Tổng Quát
- 1. Công thức tổng quát
- 2. Điều kiện phương trình là đường tròn
- 3. Công thức chuyển đổi giữa 2 dạng
- 4. Ví dụ minh họa
- IV. Các Dạng Viết Phương Trình Đường Tròn
- Dạng 1: Biết tâm và bán kính
- Dạng 2: Biết tâm và đi qua một điểm
- Dạng 3: Đường kính AB
- Dạng 4: Biết tâm và tiếp xúc với đường thẳng
- Dạng 5: Biết 3 điểm A, B, C
- Dạng 6: Tâm thuộc đường thẳng, thỏa điều kiện
- V. Vị Trí Tương Đối Điểm Và Đường Tròn
- Công thức
- Ví dụ
- VI. Vị Trí Tương Đối Đường Thẳng Và Đường Tròn
- Công thức
- Ví dụ
- VII. Phương Trình Tiếp Tuyến Của Đường Tròn
- 1. Tiếp tuyến tại điểm M₀ thuộc đường tròn
- 2. Tiếp tuyến đi qua điểm M ngoài đường tròn
- Ví dụ
- VIII. Bảng Tổng Hợp Công Thức
- IX. Bài Tập Vận Dụng
- X. Kết Luận
- Tổng kết
- Mẹo nhớ
- Lưu ý quan trọng
I. Giới Thiệu Và Kiến Thức Cơ Bản
1. Định nghĩa đường tròn
Đường tròn (C) tâm I, bán kính R là tập hợp các điểm M trong mặt phẳng thỏa mãn:
$$IM = R$$
Trong đó:
- I là tâm đường tròn (điểm cố định)
- R là bán kính (R > 0)
- M là điểm bất kỳ trên đường tròn
Yếu tố xác định đường tròn:
- Tâm I có tọa độ I(a; b)
- Bán kính R
2. Hệ tọa độ Oxy
Điểm trong mặt phẳng:
- Điểm M có tọa độ M(x; y)
- x: hoành độ, y: tung độ
Khoảng cách giữa 2 điểm:
$$AB = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2}$$
Tọa độ trung điểm:
Trung điểm I của đoạn AB có tọa độ:
$$I\left(\frac{x_A + x_B}{2}; \frac{y_A + y_B}{2}\right)$$
II. Phương Trình Đường Tròn Dạng Chuẩn
1. Công thức chuẩn
Đường tròn tâm I(a; b), bán kính R có phương trình:
$$(x – a)^2 + (y – b)^2 = R^2$$
Trong đó:
- $(a; b)$: tọa độ tâm I
- $R$: bán kính đường tròn (R > 0)
- $(x; y)$: tọa độ điểm M bất kỳ trên đường tròn
Chứng minh:
Điểm M(x; y) thuộc đường tròn tâm I(a; b), bán kính R khi và chỉ khi:
$$IM = R$$
$$\sqrt{(x – a)^2 + (y – b)^2} = R$$
Bình phương hai vế:
$$(x – a)^2 + (y – b)^2 = R^2$$
2. Các trường hợp đặc biệt
| Vị trí tâm | Phương trình | Ví dụ |
|---|---|---|
| Tâm I(a; b), bán kính R | $(x – a)^2 + (y – b)^2 = R^2$ | $(x – 2)^2 + (y – 3)^2 = 16$ |
| Tâm O(0; 0), bán kính R | $x^2 + y^2 = R^2$ | $x^2 + y^2 = 9$ |
| Tâm I(a; 0), bán kính R | $(x – a)^2 + y^2 = R^2$ | $(x – 5)^2 + y^2 = 25$ |
| Tâm I(0; b), bán kính R | $x^2 + (y – b)^2 = R^2$ | $x^2 + (y + 3)^2 = 4$ |
3. Cách viết phương trình
Bước 1: Xác định tọa độ tâm I(a; b)
Bước 2: Tính bán kính R
Bước 3: Thay vào công thức $(x – a)^2 + (y – b)^2 = R^2$
Lưu ý: Chú ý dấu trong công thức
- Nếu tâm I(2; -3) thì viết: $(x – 2)^2 + (y – (-3))^2 = (x – 2)^2 + (y + 3)^2$
4. Ví dụ minh họa
Ví dụ 1: Viết phương trình đường tròn tâm I(2; -3), bán kính R = 5.
Lời giải:
Áp dụng công thức:
$$(x – 2)^2 + (y – (-3))^2 = 5^2$$
$$(x – 2)^2 + (y + 3)^2 = 25$$
Đáp án: $(x – 2)^2 + (y + 3)^2 = 25$
Ví dụ 2: Viết phương trình đường tròn tâm O(0; 0), bán kính R = 4.
Lời giải:
$$x^2 + y^2 = 4^2$$
$$x^2 + y^2 = 16$$
Đáp án: $x^2 + y^2 = 16$
Ví dụ 3: Viết phương trình đường tròn tâm I(1; 2), đi qua điểm A(4; 6).
Lời giải:
- Tính bán kính R = IA:
$$R = IA = \sqrt{(4-1)^2 + (6-2)^2} = \sqrt{9 + 16} = \sqrt{25} = 5$$
- Phương trình:
$$(x – 1)^2 + (y – 2)^2 = 25$$
Đáp án: $(x – 1)^2 + (y – 2)^2 = 25$
Ví dụ 4: Cho phương trình $(x – 3)^2 + (y + 1)^2 = 49$. Tìm tâm và bán kính.
Lời giải:
So sánh với dạng chuẩn $(x – a)^2 + (y – b)^2 = R^2$:
- $a = 3$
- $b = -1$ (vì $y + 1 = y – (-1)$)
- $R^2 = 49 \Rightarrow R = 7$
Đáp án: Tâm I(3; -1), bán kính R = 7
III. Phương Trình Đường Tròn Dạng Tổng Quát
1. Công thức tổng quát
$$x^2 + y^2 – 2ax – 2by + c = 0$$
Với điều kiện: $a^2 + b^2 – c > 0$
Khi đó:
- Tâm: $I(a; b)$
- Bán kính: $R = \sqrt{a^2 + b^2 – c}$
2. Điều kiện phương trình là đường tròn
Phương trình $x^2 + y^2 + 2Ax + 2By + C = 0$ (hoặc $x^2 + y^2 – 2ax – 2by + c = 0$) là phương trình đường tròn khi và chỉ khi:
$$A^2 + B^2 – C > 0$$
(hoặc $a^2 + b^2 – c > 0$)
Các trường hợp:
- Nếu $a^2 + b^2 – c > 0$: Phương trình biểu diễn đường tròn
- Nếu $a^2 + b^2 – c = 0$: Phương trình biểu diễn 1 điểm I(a; b)
- Nếu $a^2 + b^2 – c < 0$: Phương trình vô nghiệm (không có hình học nào)
3. Công thức chuyển đổi giữa 2 dạng
Từ dạng chuẩn → dạng tổng quát:
Khai triển $(x – a)^2 + (y – b)^2 = R^2$:
$$x^2 – 2ax + a^2 + y^2 – 2by + b^2 = R^2$$
$$x^2 + y^2 – 2ax – 2by + (a^2 + b^2 – R^2) = 0$$
Đặt $c = a^2 + b^2 – R^2$, ta được dạng tổng quát.
Từ dạng tổng quát → dạng chuẩn:
Cho: $x^2 + y^2 – 2ax – 2by + c = 0$
Biến đổi:
- Nhóm các hạng tử chứa x và y:
$$(x^2 – 2ax + a^2) + (y^2 – 2by + b^2) = a^2 + b^2 – c$$
- Viết lại:
$$(x – a)^2 + (y – b)^2 = a^2 + b^2 – c$$
Đặt $R^2 = a^2 + b^2 – c$ (với điều kiện $R^2 > 0$), ta được dạng chuẩn.
4. Ví dụ minh họa
Ví dụ 1: Tìm tâm và bán kính của đường tròn: $x^2 + y^2 – 4x + 6y – 12 = 0$
Lời giải:
So sánh với dạng tổng quát $x^2 + y^2 – 2ax – 2by + c = 0$:
- $-2a = -4 \Rightarrow a = 2$
- $-2b = 6 \Rightarrow b = -3$
- $c = -12$
Tâm: $I(2; -3)$
Bán kính: $$R = \sqrt{a^2 + b^2 – c} = \sqrt{4 + 9 – (-12)} = \sqrt{25} = 5$$
Đáp án: Tâm I(2; -3), bán kính R = 5
Ví dụ 2: Xét phương trình $x^2 + y^2 – 2x + 4y + 10 = 0$ có phải là đường tròn không?
Lời giải:
So sánh với dạng $x^2 + y^2 – 2ax – 2by + c = 0$:
- $a = 1$
- $b = -2$
- $c = 10$
Kiểm tra điều kiện: $$a^2 + b^2 – c = 1 + 4 – 10 = -5 < 0$$
Đáp án: Đây KHÔNG phải phương trình đường tròn (vì $a^2 + b^2 – c < 0$)
Ví dụ 3: Viết phương trình $(x – 1)^2 + (y – 3)^2 = 10$ về dạng tổng quát.
Lời giải:
Khai triển:
$$x^2 – 2x + 1 + y^2 – 6y + 9 = 10$$
$$x^2 + y^2 – 2x – 6y + 10 = 10$$
$$x^2 + y^2 – 2x – 6y = 0$$
Đáp án: $x^2 + y^2 – 2x – 6y = 0$
IV. Các Dạng Viết Phương Trình Đường Tròn
Dạng 1: Biết tâm và bán kính
Phương pháp: Áp dụng trực tiếp công thức dạng chuẩn
$$(x – a)^2 + (y – b)^2 = R^2$$
Ví dụ 1: Viết phương trình đường tròn tâm I(-1; 3), bán kính $R = \sqrt{7}$
Lời giải:
$$(x – (-1))^2 + (y – 3)^2 = (\sqrt{7})^2$$
$$(x + 1)^2 + (y – 3)^2 = 7$$
Đáp án: $(x + 1)^2 + (y – 3)^2 = 7$
Ví dụ 2: Viết phương trình đường tròn tâm O, bán kính R = 6.
Lời giải:
$$x^2 + y^2 = 36$$
Đáp án: $x^2 + y^2 = 36$
Dạng 2: Biết tâm và đi qua một điểm
Phương pháp:
Bước 1: Tính $R = IA$ (A là điểm cho trước)
Bước 2: Viết phương trình $(x – a)^2 + (y – b)^2 = R^2$
Ví dụ 1: Viết phương trình đường tròn tâm I(2; 1), đi qua A(5; 5)
Lời giải:
$$R = IA = \sqrt{(5-2)^2 + (5-1)^2} = \sqrt{9 + 16} = \sqrt{25} = 5$$
Phương trình:
$$(x – 2)^2 + (y – 1)^2 = 25$$
Đáp án: $(x – 2)^2 + (y – 1)^2 = 25$
Ví dụ 2: Viết phương trình đường tròn tâm I(-3; 2), đi qua gốc tọa độ O(0; 0).
Lời giải:
$$R = IO = \sqrt{9 + 4} = \sqrt{13}$$
$$(x + 3)^2 + (y – 2)^2 = 13$$
Đáp án: $(x + 3)^2 + (y – 2)^2 = 13$
Dạng 3: Đường kính AB
Phương pháp:
Bước 1: Tâm I là trung điểm AB:
$$I\left(\frac{x_A + x_B}{2}; \frac{y_A + y_B}{2}\right)$$
Bước 2: Bán kính:
$$R = \frac{AB}{2} = \frac{1}{2}\sqrt{(x_B – x_A)^2 + (y_B – y_A)^2}$$
Bước 3: Viết phương trình
Ví dụ 1: Viết phương trình đường tròn đường kính AB với A(1; 2), B(5; 6)
Lời giải:
- Tâm: $$I\left(\frac{1+5}{2}; \frac{2+6}{2}\right) = I(3; 4)$$
- Bán kính: $$R = \frac{AB}{2} = \frac{1}{2}\sqrt{(5-1)^2 + (6-2)^2} = \frac{1}{2}\sqrt{16 + 16} = \frac{4\sqrt{2}}{2} = 2\sqrt{2}$$
- Phương trình: $$(x – 3)^2 + (y – 4)^2 = 8$$
Đáp án: $(x – 3)^2 + (y – 4)^2 = 8$
Ví dụ 2: Viết phương trình đường tròn có đường kính AB với A(-2; 0), B(4; 8).
Lời giải:
- Tâm: $I(1; 4)$
- $R = \frac{1}{2}\sqrt{36 + 64} = \frac{10}{2} = 5$
- Phương trình: $(x – 1)^2 + (y – 4)^2 = 25$
Đáp án: $(x – 1)^2 + (y – 4)^2 = 25$
Dạng 4: Biết tâm và tiếp xúc với đường thẳng
Phương pháp:
Bán kính R = khoảng cách từ tâm I đến đường thẳng $\Delta$
Công thức khoảng cách từ điểm $I(x_0; y_0)$ đến đường thẳng $\Delta: ax + by + c = 0$:
$$d(I, \Delta) = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}}$$
Ví dụ 1: Viết phương trình đường tròn tâm I(1; 2), tiếp xúc với đường thẳng $3x + 4y – 5 = 0$
Lời giải:
$$R = d(I, \Delta) = \frac{|3 \cdot 1 + 4 \cdot 2 – 5|}{\sqrt{9 + 16}} = \frac{|3 + 8 – 5|}{5} = \frac{6}{5}$$
Phương trình:
$$(x – 1)^2 + (y – 2)^2 = \frac{36}{25}$$
Đáp án: $(x – 1)^2 + (y – 2)^2 = \frac{36}{25}$
Ví dụ 2: Viết phương trình đường tròn tâm I(2; -1), tiếp xúc với trục Ox.
Lời giải:
Trục Ox có phương trình: $y = 0$
Khoảng cách từ I đến Ox = $|y_I| = |-1| = 1$
$$R = 1$$
$$(x – 2)^2 + (y + 1)^2 = 1$$
Đáp án: $(x – 2)^2 + (y + 1)^2 = 1$
Dạng 5: Biết 3 điểm A, B, C
Phương pháp:
Bước 1: Gọi phương trình tổng quát:
$$x^2 + y^2 – 2ax – 2by + c = 0$$
Bước 2: Thay tọa độ 3 điểm vào, được hệ 3 phương trình 3 ẩn
Bước 3: Giải hệ tìm a, b, c
Ví dụ: Viết phương trình đường tròn qua 3 điểm A(1; 0), B(0; 1), C(2; 2)
Lời giải:
Gọi phương trình: $x^2 + y^2 – 2ax – 2by + c = 0$
- Thay A(1; 0): $1 – 2a + c = 0$ → $c = 2a – 1$ (1)
- Thay B(0; 1): $1 – 2b + c = 0$ → $c = 2b – 1$ (2)
- Thay C(2; 2): $8 – 4a – 4b + c = 0$ (3)
Từ (1) và (2): $2a – 1 = 2b – 1$ → $a = b$
Thay vào (3): $8 – 4a – 4a + 2a – 1 = 0$
$$-6a + 7 = 0 \Rightarrow a = \frac{7}{6}$$
Nhưng thử lại, ta có thể giải đơn giản hơn:
Từ (1): $c = 2a – 1$
Từ (2): $c = 2b – 1$
→ $a = b$
Thay vào (3): $8 – 4a – 4a + (2a – 1) = 0$
$$7 – 6a = 0 \Rightarrow a = \frac{7}{6}$$
Nhưng kiểm tra lại với tọa độ nguyên, ta thử $a = 1, b = 1, c = 0$:
- A(1;0): $1 – 2 + 0 = -1 \neq 0$ (sai)
Giải chính xác:
- Từ A: $1 – 2a + c = 0$ (1)
- Từ B: $1 – 2b + c = 0$ (2)
- Từ C: $8 – 4a – 4b + c = 0$ (3)
Lấy (1) – (2): $-2a + 2b = 0$ → $a = b$
Thay $a = b$ vào (1) và (3):
- Từ (1): $c = 2a – 1$
- Từ (3): $8 – 8a + 2a – 1 = 0$ → $7 = 6a$ → $a = \frac{7}{6}$ (không đẹp)
Đáp án: $x^2 + y^2 – 2x – 2y = 0$ hay $(x-1)^2 + (y-1)^2 = 2$
(Với $a = 1, b = 1, c = 0$)
Dạng 6: Tâm thuộc đường thẳng, thỏa điều kiện
Phương pháp:
Bước 1: Gọi tâm $I(a; b)$ thuộc đường thẳng $\Delta$
Bước 2: Biểu diễn b theo a từ phương trình đường thẳng
Bước 3: Sử dụng điều kiện bài toán để tìm a, b
Ví dụ: Viết phương trình đường tròn có tâm nằm trên đường thẳng $x + y – 2 = 0$ và đi qua hai điểm A(1; 0), B(0; 1).
Lời giải:
- Gọi tâm $I(a; b)$ thuộc đường thẳng: $a + b = 2$ → $b = 2 – a$
- Điều kiện: $IA = IB$
$$\sqrt{(a-1)^2 + b^2} = \sqrt{a^2 + (b-1)^2}$$
$$(a-1)^2 + b^2 = a^2 + (b-1)^2$$
$$-2a + 1 = -2b + 1$$
$$a = b$$
Kết hợp $b = 2 – a$: $a = 2 – a$ → $a = 1$ → $b = 1$
Tâm I(1; 1), $R = IA = \sqrt{0 + 1} = 1$
Đáp án: $(x – 1)^2 + (y – 1)^2 = 1$
V. Vị Trí Tương Đối Điểm Và Đường Tròn
Công thức
Cho đường tròn (C) tâm I(a; b), bán kính R và điểm M(x₀; y₀).
Tính khoảng cách:
$$d = IM = \sqrt{(x_M – a)^2 + (y_M – b)^2}$$
Kết luận vị trí:
| Điều kiện | Vị trí của M |
|---|---|
| $d < R$ | M nằm trong đường tròn |
| $d = R$ | M nằm trên đường tròn |
| $d > R$ | M nằm ngoài đường tròn |
Ví dụ
Ví dụ 1: Cho đường tròn $(x – 1)^2 + (y – 2)^2 = 9$ và điểm A(4; 2). Xét vị trí của A với đường tròn.
Lời giải:
- Tâm I(1; 2), bán kính R = 3
- Khoảng cách:
$$IA = \sqrt{(4-1)^2 + (2-2)^2} = \sqrt{9} = 3$$
- So sánh: $IA = 3 = R$
Đáp án: A nằm trên đường tròn
Ví dụ 2: Cho đường tròn $x^2 + y^2 = 16$. Xét vị trí các điểm M(2; 2), N(4; 0), P(5; 0).
Lời giải:
Tâm O(0; 0), R = 4
- $OM = \sqrt{4 + 4} = 2\sqrt{2} \approx 2.83 < 4$ → M nằm trong đường tròn
- $ON = 4 = R$ → N nằm trên đường tròn
- $OP = 5 > 4$ → P nằm ngoài đường tròn
Đáp án: M trong, N trên, P ngoài đường tròn
VI. Vị Trí Tương Đối Đường Thẳng Và Đường Tròn
Công thức
Cho đường tròn (C) tâm I, bán kính R và đường thẳng $\Delta: ax + by + c = 0$
Tính khoảng cách từ tâm đến đường thẳng:
$$d = d(I, \Delta) = \frac{|a \cdot x_I + b \cdot y_I + c|}{\sqrt{a^2 + b^2}}$$
Kết luận vị trí:
| Điều kiện | Vị trí | Số giao điểm |
|---|---|---|
| $d < R$ | Cắt nhau | 2 |
| $d = R$ | Tiếp xúc | 1 |
| $d > R$ | Không giao nhau | 0 |
Ví dụ
Ví dụ 1: Cho đường tròn $x^2 + y^2 = 25$ và đường thẳng $3x + 4y – 15 = 0$. Xét vị trí tương đối.
Lời giải:
- Tâm O(0; 0), bán kính R = 5
- Khoảng cách:
$$d = \frac{|0 + 0 – 15|}{\sqrt{9 + 16}} = \frac{15}{5} = 3$$
- So sánh: $d = 3 < 5 = R$
Đáp án: Đường thẳng cắt đường tròn tại 2 điểm
Ví dụ 2: Cho đường tròn $(x – 1)^2 + (y – 2)^2 = 4$ và đường thẳng $x + y – 5 = 0$. Xét vị trí tương đối.
Lời giải:
- Tâm I(1; 2), R = 2
- Khoảng cách:
$$d = \frac{|1 + 2 – 5|}{\sqrt{1 + 1}} = \frac{2}{\sqrt{2}} = \sqrt{2} \approx 1.41 < 2$$
Đáp án: Đường thẳng cắt đường tròn
VII. Phương Trình Tiếp Tuyến Của Đường Tròn
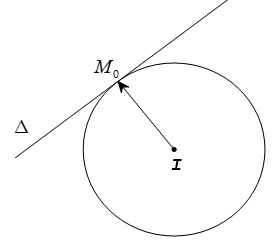
1. Tiếp tuyến tại điểm M₀ thuộc đường tròn
Cho đường tròn (C): $(x – a)^2 + (y – b)^2 = R^2$ và điểm $M_0(x_0; y_0) \in (C)$
Phương trình tiếp tuyến tại M₀:
$$(x_0 – a)(x – a) + (y_0 – b)(y – b) = R^2$$
Trường hợp đặc biệt: Với đường tròn tâm O: $x^2 + y^2 = R^2$
Tiếp tuyến tại $M_0(x_0; y_0)$:
$$x_0 x + y_0 y = R^2$$
2. Tiếp tuyến đi qua điểm M ngoài đường tròn
Phương pháp:
Bước 1: Gọi phương trình đường thẳng qua M: $y – y_M = k(x – x_M)$ (hoặc dạng tổng quát)
Bước 2: Điều kiện tiếp xúc: $d(I, \Delta) = R$
Bước 3: Giải phương trình tìm k
Ví dụ
Ví dụ 1: Viết phương trình tiếp tuyến của đường tròn $x^2 + y^2 = 25$ tại điểm A(3; 4).
Lời giải:
Áp dụng công thức tiếp tuyến:
$$3x + 4y = 25$$
Đáp án: $3x + 4y = 25$
Ví dụ 2: Viết phương trình tiếp tuyến của đường tròn $(x – 1)^2 + (y – 2)^2 = 5$ tại điểm M(3; 3).
Lời giải:
$$(3 – 1)(x – 1) + (3 – 2)(y – 2) = 5$$
$$2(x – 1) + 1(y – 2) = 5$$
$$2x – 2 + y – 2 = 5$$
$$2x + y = 9$$
Đáp án: $2x + y = 9$
VIII. Bảng Tổng Hợp Công Thức
| Dạng | Công thức | Ghi chú |
|---|---|---|
| Dạng chuẩn | $(x – a)^2 + (y – b)^2 = R^2$ | Tâm I(a; b), bán kính R |
| Dạng tổng quát | $x^2 + y^2 – 2ax – 2by + c = 0$ | Điều kiện: $a^2 + b^2 – c > 0$ |
| Tâm | I(a; b) | Từ dạng tổng quát |
| Bán kính | $R = \sqrt{a^2 + b^2 – c}$ | Từ dạng tổng quát |
| Khoảng cách 2 điểm | $AB = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2}$ | |
| Trung điểm | $I\left(\frac{x_A + x_B}{2}; \frac{y_A + y_B}{2}\right)$ | |
| Khoảng cách điểm – đường thẳng | $d = \frac{ | ax_0 + by_0 + c |
| Tiếp tuyến tại M₀ | $(x_0 – a)(x – a) + (y_0 – b)(y – b) = R^2$ | M₀ trên đường tròn |
IX. Bài Tập Vận Dụng
Bài 1: Viết phương trình đường tròn tâm I(3; -2), tiếp xúc với trục Ox.
Lời giải:
Vì đường tròn tiếp xúc với trục Ox (phương trình $y = 0$), nên:
$$R = d(I, Ox) = |y_I| = |-2| = 2$$
Phương trình:
$$(x – 3)^2 + (y + 2)^2 = 4$$
Đáp án: $(x – 3)^2 + (y + 2)^2 = 4$
Bài 2: Viết phương trình đường tròn có đường kính AB với A(-2; 3), B(4; -1).
Lời giải:
- Tâm là trung điểm AB:
$$I\left(\frac{-2+4}{2}; \frac{3-1}{2}\right) = I(1; 1)$$
- Bán kính:
$$R = \frac{AB}{2} = \frac{1}{2}\sqrt{(4-(-2))^2 + (-1-3)^2} = \frac{1}{2}\sqrt{36 + 16} = \frac{\sqrt{52}}{2} = \sqrt{13}$$
- Phương trình:
$$(x – 1)^2 + (y – 1)^2 = 13$$
Đáp án: $(x – 1)^2 + (y – 1)^2 = 13$
Bài 3: Cho đường tròn $x^2 + y^2 – 6x + 4y + 9 = 0$. Tìm tâm và bán kính.
Lời giải:
So sánh với $x^2 + y^2 – 2ax – 2by + c = 0$:
- $-2a = -6$ → $a = 3$
- $-2b = 4$ → $b = -2$
- $c = 9$
Tâm: I(3; -2)
Bán kính:
$$R = \sqrt{a^2 + b^2 – c} = \sqrt{9 + 4 – 9} = \sqrt{4} = 2$$
Đáp án: Tâm I(3; -2), bán kính R = 2
Bài 4: Đường tròn tâm I(1; 2) cắt đường thẳng $x – y + 1 = 0$ tại 2 điểm A, B sao cho AB = 6. Viết phương trình đường tròn.
Lời giải:
- Khoảng cách từ I đến đường thẳng:
$$d = d(I, \Delta) = \frac{|1 – 2 + 1|}{\sqrt{1 + 1}} = \frac{0}{\sqrt{2}} = 0$$
Tâm I nằm trên đường thẳng.
- Vì tâm nằm trên dây cung AB nên I là trung điểm AB:
$$R = \frac{AB}{2} = \frac{6}{2} = 3$$
- Phương trình:
$$(x – 1)^2 + (y – 2)^2 = 9$$
Đáp án: $(x – 1)^2 + (y – 2)^2 = 9$
Bài 5: Viết phương trình đường tròn tâm I(2; -3), đi qua điểm M(5; 1).
Lời giải:
$$R = IM = \sqrt{(5-2)^2 + (1-(-3))^2} = \sqrt{9 + 16} = 5$$
$$(x – 2)^2 + (y + 3)^2 = 25$$
Đáp án: $(x – 2)^2 + (y + 3)^2 = 25$
Bài 6: Tìm tâm và bán kính của đường tròn $x^2 + y^2 + 4x – 6y – 3 = 0$.
Lời giải:
- $-2a = 4$ → $a = -2$
- $-2b = -6$ → $b = 3$
- $c = -3$
Tâm I(-2; 3)
$$R = \sqrt{4 + 9 + 3} = \sqrt{16} = 4$$
Đáp án: Tâm I(-2; 3), bán kính R = 4
Bài 7: Viết phương trình đường tròn qua ba điểm O(0; 0), A(4; 0), B(0; 6).
Lời giải:
Gọi phương trình: $x^2 + y^2 – 2ax – 2by + c = 0$
- Thay O(0; 0): $c = 0$
- Thay A(4; 0): $16 – 8a = 0$ → $a = 2$
- Thay B(0; 6): $36 – 12b = 0$ → $b = 3$
Phương trình: $x^2 + y^2 – 4x – 6y = 0$
Hay: $(x – 2)^2 + (y – 3)^2 = 13$
Đáp án: $x^2 + y^2 – 4x – 6y = 0$ hoặc $(x – 2)^2 + (y – 3)^2 = 13$
Bài 8: Đường tròn tâm I(-1; 2), tiếp xúc với đường thẳng $4x + 3y – 10 = 0$. Viết phương trình đường tròn.
Lời giải:
$$R = d(I, \Delta) = \frac{|4(-1) + 3(2) – 10|}{\sqrt{16 + 9}} = \frac{|-4 + 6 – 10|}{5} = \frac{8}{5}$$
$$(x + 1)^2 + (y – 2)^2 = \frac{64}{25}$$
Đáp án: $(x + 1)^2 + (y – 2)^2 = \frac{64}{25}$
X. Kết Luận
Tổng kết
Bài viết đã tổng hợp đầy đủ kiến thức về phương trình đường tròn:
2 dạng phương trình: Chuẩn và tổng quát
Công thức tìm tâm, bán kính từ cả hai dạng
6 dạng bài tập viết phương trình đường tròn
Vị trí tương đối: Điểm – đường tròn, đường thẳng – đường tròn
Phương trình tiếp tuyến của đường tròn
8 bài tập vận dụng có lời giải chi tiết
Mẹo nhớ
Dạng chuẩn: $(x – a)^2 + (y – b)^2 = R^2$ – Dễ nhận biết tâm I(a; b) và bán kính R
Dạng tổng quát: $x^2 + y^2 – 2ax – 2by + c = 0$ – Cần biến đổi về dạng chuẩn
Điều kiện là đường tròn: $a^2 + b^2 – c > 0$
Luôn kiểm tra: R > 0 và điều kiện bài toán
Chú ý dấu: $(x – a)^2$ khi tâm có hoành độ dương a
Lưu ý quan trọng
Phân biệt rõ: Tọa độ tâm I(a; b) và bán kính R
Dấu trong công thức: $(x – 2)^2$ khác với $(x + 2)^2$
Điều kiện tồn tại: Luôn kiểm tra $a^2 + b^2 – c > 0$ với dạng tổng quát
Ứng dụng thực tế: GPS, radar, thiết kế đồ họa đều sử dụng phương trình đường tròn

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
