Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ HÌNH BÌNH HÀNH
- 1. Hình bình hành là gì?
- 2. Tính chất cơ bản của hình bình hành
- 3. Các dạng đặc biệt của hình bình hành
- 4. Cấu trúc bài viết
- II. CÔNG THỨC CHU VI HÌNH BÌNH HÀNH
- 1. Định nghĩa chu vi
- 2. Công thức tính chu vi cơ bản
- 3. Công thức chu vi khi biết các yếu tố khác
- 4. Lưu ý khi tính chu vi
- 5. Bài tập tự luyện
- III. CÔNG THỨC DIỆN TÍCH HÌNH BÌNH HÀNH
- 1. Định nghĩa diện tích
- 2. Công thức diện tích cơ bản
- 3. Công thức diện tích khi biết hai cạnh và góc
- 4. Công thức diện tích khi biết đường chéo
- 5. Công thức diện tích trong hệ tọa độ
- 6. Các công thức phụ liên quan đến diện tích
- 7. So sánh diện tích hình bình hành với các hình khác
- IV. CÔNG THỨC ĐƯỜNG CHÉO HÌNH BÌNH HÀNH
- 1. Tính chất đường chéo
- 2. Công thức tính độ dài đường chéo
- 3. Công thức tính đường chéo khi biết cạnh và góc
- 4. Công thức đường chéo trong hệ tọa độ
- 5. Tính góc giữa hai đường chéo
- V. CÁC CÔNG THỨC LIÊN QUAN KHÁC
- 1. Công thức tính chiều cao
- 2. Công thức tính góc
- 3. Công thức tính cạnh
- 4. Bảng tổng hợp các công thức quan trọng
- VI. CÁCH NHẬN BIẾT VÀ CHỨNG MINH HÌNH BÌNH HÀNH
- 1. Dấu hiệu nhận biết hình bình hành
- 2. Phương pháp chứng minh
- 3. Phân biệt hình bình hành với các hình khác
- VII. VÍ DỤ TỔNG HỢP VÀ BÀI TẬP ÁP DỤNG
- Dạng 1: Tính chu vi hình bình hành
- Dạng 2: Tính diện tích hình bình hành
- Dạng 3: Tính đường chéo
- Dạng 4: Bài toán tổng hợp
- VIII. MẸO VÀ LƯU Ý KHI HỌC HÌNH BÌNH HÀNH
- 1. Các sai lầm thường gặp
- 2. Mẹo nhớ công thức
- 3. Phương pháp giải bài tập hiệu quả
- 4. Kỹ thuật vẽ hình bình hành chuẩn
- IX. ỨNG DỤNG THỰC TẾ CỦA HÌNH BÌNH HÀNH
- 1. Trong kiến trúc và xây dựng
- 2. Trong kỹ thuật cơ khí
- 3. Trong đồ chơi và giải trí
- 4. Trong nghệ thuật và thiết kế
- 5. Trong khoa học
- X. KẾT LUẬN
- Tổng kết
- Tầm quan trọng của hình bình hành
I. GIỚI THIỆU VỀ HÌNH BÌNH HÀNH
1. Hình bình hành là gì?
Định nghĩa: Hình bình hành là tứ giác có các cạnh đối song song với nhau.
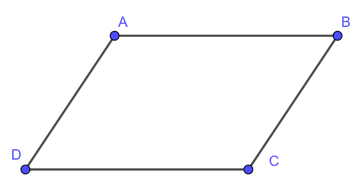
Ký hiệu: ABCD là hình bình hành, viết: $ABCD$ hoặc $\square ABCD$
Vị trí trong hình học: Hình bình hành thuộc họ tứ giác đặc biệt, là trường hợp riêng của hình thang (có hai đáy song song và bằng nhau).
2. Tính chất cơ bản của hình bình hành
Các tính chất quan trọng:
- Về cạnh: Các cạnh đối bằng nhau ($AB = CD$, $BC = AD$)
- Về góc: Các góc đối bằng nhau ($\angle A = \angle C$, $\angle B = \angle D$)
- Góc kề: Hai góc kề bù nhau ($\angle A + \angle B = 180°$)
- Đường chéo: Hai đường chéo cắt nhau tại trung điểm mỗi đường ($OA = OC$, $OB = OD$)
- Tâm đối xứng: Điểm cắt O của hai đường chéo là tâm đối xứng
3. Các dạng đặc biệt của hình bình hành
Hình bình hành có 3 dạng đặc biệt:
- Hình chữ nhật: Hình bình hành có một góc vuông (→ có 4 góc vuông)
- Hình thoi: Hình bình hành có hai cạnh kề bằng nhau (→ có 4 cạnh bằng nhau)
- Hình vuông: Hình bình hành vừa là hình chữ nhật, vừa là hình thoi
4. Cấu trúc bài viết
Bài viết sẽ tổng hợp đầy đủ:
- Công thức tính chu vi hình bình hành
- Công thức tính diện tích hình bình hành (nhiều cách)
- Công thức tính đường chéo hình bình hành
- Các công thức liên quan (chiều cao, góc, cạnh)
- Ví dụ minh họa chi tiết
- Bài tập áp dụng có lời giải
II. CÔNG THỨC CHU VI HÌNH BÌNH HÀNH
1. Định nghĩa chu vi
Chu vi hình bình hành là tổng độ dài tất cả các cạnh của hình bình hành.
Ký hiệu: $P$ (Perimeter)
2. Công thức tính chu vi cơ bản
Công thức 1: Khi biết độ dài 2 cạnh kề
$$P = 2(a + b)$$
Trong đó:
- $P$: Chu vi hình bình hành
- $a$: Độ dài cạnh đáy
- $b$: Độ dài cạnh bên
Giải thích: Vì hình bình hành có các cạnh đối bằng nhau nên chu vi = 2 lần tổng hai cạnh kề.
Ví dụ 1:
- Cho hình bình hành ABCD có $AB = 8$ cm, $BC = 5$ cm
- Tính chu vi: $P = 2(AB + BC) = 2(8 + 5) = 2 \times 13 = 26$ cm
- Đáp số: 26 cm
3. Công thức chu vi khi biết các yếu tố khác
Công thức 2: Trong hệ tọa độ
Cho hình bình hành ABCD với tọa độ:
- $A(x_1, y_1)$, $B(x_2, y_2)$, $D(x_4, y_4)$
Chu vi: $$P = 2(AB + AD)$$
Trong đó:
- $AB = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}$
- $AD = \sqrt{(x_4 – x_1)^2 + (y_4 – y_1)^2}$
Ví dụ 2:
- Cho $A(1, 2)$, $B(4, 3)$, $D(2, 5)$
- Tính $AB = \sqrt{(4-1)^2 + (3-2)^2} = \sqrt{9 + 1} = \sqrt{10}$
- Tính $AD = \sqrt{(2-1)^2 + (5-2)^2} = \sqrt{1 + 9} = \sqrt{10}$
- Chu vi: $P = 2(\sqrt{10} + \sqrt{10}) = 4\sqrt{10}$ (đơn vị)
- Đáp số: $4\sqrt{10}$ ≈ 12.65 đơn vị
4. Lưu ý khi tính chu vi
- Đơn vị đo phải thống nhất (cm, m, dm…)
- Chu vi luôn là số dương
- Nếu đề cho một cạnh và chu vi, có thể suy ra cạnh còn lại: $b = \frac{P}{2} – a$
5. Bài tập tự luyện
Bài 1: Hình bình hành có chu vi 36 cm, một cạnh dài 10 cm. Tính cạnh còn lại.
Lời giải:
- $2(a + b) = 36$, với $a = 10$
- $2(10 + b) = 36$
- $20 + 2b = 36$
- $2b = 16$, $b = 8$ cm
- Đáp số: 8 cm
Bài 2: Hình bình hành có hai cạnh kề tỉ lệ 3:5 và chu vi 48 cm. Tính độ dài mỗi cạnh.
Lời giải:
- Gọi hai cạnh là $3x$ và $5x$
- $P = 2(3x + 5x) = 16x = 48$
- $x = 3$
- Hai cạnh: $3 \times 3 = 9$ cm và $5 \times 3 = 15$ cm
- Đáp số: 9 cm và 15 cm
III. CÔNG THỨC DIỆN TÍCH HÌNH BÌNH HÀNH
1. Định nghĩa diện tích
Diện tích hình bình hành là số đo phần mặt phẳng giới hạn bởi hình bình hành.
Ký hiệu: $S$ (Surface area)
Đơn vị: cm², m², dm², km²…
2. Công thức diện tích cơ bản
Công thức 1: Diện tích = Đáy × Chiều cao
$$S = a \times h$$
Trong đó:
- $S$: Diện tích hình bình hành
- $a$: Độ dài cạnh đáy
- $h$: Chiều cao tương ứng với cạnh đáy (khoảng cách từ đỉnh đến đáy)
Giải thích:
- Chiều cao $h$ là đoạn vuông góc từ một đỉnh xuống cạnh đối diện (hoặc kéo dài của nó)
- Công thức này giống công thức diện tích hình chữ nhật
Ví dụ 3:
- Cho hình bình hành ABCD có đáy $AB = 12$ cm, chiều cao $h = 5$ cm
- Diện tích: $S = 12 \times 5 = 60$ cm²
- Đáp số: 60 cm²
3. Công thức diện tích khi biết hai cạnh và góc
Công thức 2: Sử dụng sin của góc
$$S = a \times b \times \sin \alpha$$
Trong đó:
- $a$, $b$: Độ dài hai cạnh kề
- $\alpha$: Góc giữa hai cạnh đó
- $\sin \alpha$: Sin của góc $\alpha$
Giải thích:
- Từ công thức $S = a \times h$
- Ta có: $h = b \times \sin \alpha$ (chiều cao trong tam giác)
- Nên: $S = a \times (b \times \sin \alpha) = a \times b \times \sin \alpha$
Ví dụ 4:
- Cho hình bình hành có $a = 8$ cm, $b = 6$ cm, $\alpha = 30°$
- Diện tích: $S = 8 \times 6 \times \sin 30° = 48 \times 0.5 = 24$ cm²
- Đáp số: 24 cm²
Lưu ý quan trọng:
- Có thể dùng góc $\alpha$ hoặc góc kề bù $(180° – \alpha)$ vì $\sin \alpha = \sin(180° – \alpha)$
- Nếu $\alpha = 90°$ thì hình bình hành trở thành hình chữ nhật: $S = a \times b$
4. Công thức diện tích khi biết đường chéo
Công thức 3: Sử dụng hai đường chéo và góc giữa chúng
$$S = \frac{1}{2} \times d_1 \times d_2 \times \sin \theta$$
Trong đó:
- $d_1$, $d_2$: Độ dài hai đường chéo
- $\theta$: Góc giữa hai đường chéo
Giải thích:
- Hai đường chéo chia hình bình hành thành 4 tam giác
- Diện tích mỗi tam giác = $\frac{1}{4} d_1 \times d_2 \times \sin \theta$
- Tổng diện tích = $4 \times \frac{1}{4} d_1 \times d_2 \times \sin \theta = \frac{1}{2} d_1 \times d_2 \times \sin \theta$
Ví dụ 5:
- Cho hình bình hành có hai đường chéo $d_1 = 10$ cm, $d_2 = 8$ cm
- Góc giữa hai đường chéo $\theta = 60°$
- Diện tích: $S = \frac{1}{2} \times 10 \times 8 \times \sin 60° = \frac{1}{2} \times 10 \times 8 \times \frac{\sqrt{3}}{2} = 20\sqrt{3}$ cm²
- Đáp số: $20\sqrt{3}$ cm² ≈ 34.64 cm²
Trường hợp đặc biệt:
- Nếu hai đường chéo vuông góc ($\theta = 90°$), thì $\sin 90° = 1$
- $\Rightarrow S = \frac{1}{2} d_1 \times d_2$ (công thức diện tích hình thoi)
5. Công thức diện tích trong hệ tọa độ
Công thức 4: Sử dụng tọa độ các đỉnh
Cho hình bình hành ABCD với tọa độ $A(x_1, y_1)$, $B(x_2, y_2)$, $D(x_4, y_4)$
$$S = |\overrightarrow{AB} \times \overrightarrow{AD}|$$
Trong đó:
- $\overrightarrow{AB} = (x_2 – x_1, y_2 – y_1)$
- $\overrightarrow{AD} = (x_4 – x_1, y_4 – y_1)$
- Tích có hướng: $\overrightarrow{AB} \times \overrightarrow{AD} = (x_2 – x_1)(y_4 – y_1) – (y_2 – y_1)(x_4 – x_1)$
Ví dụ 6:
- Cho $A(1, 1)$, $B(4, 2)$, $D(2, 4)$
- $\overrightarrow{AB} = (3, 1)$, $\overrightarrow{AD} = (1, 3)$
- $S = |3 \times 3 – 1 \times 1| = |9 – 1| = 8$ (đơn vị diện tích)
- Đáp số: 8 đơn vị diện tích
6. Các công thức phụ liên quan đến diện tích
Công thức tính chiều cao khi biết diện tích:
$$h = \frac{S}{a}$$
Công thức tính cạnh đáy khi biết diện tích:
$$a = \frac{S}{h}$$
Ví dụ 7:
- Hình bình hành có diện tích 48 cm², chiều cao 6 cm. Tính cạnh đáy.
- $a = \frac{48}{6} = 8$ cm
- Đáp số: 8 cm
7. So sánh diện tích hình bình hành với các hình khác
| Hình | Công thức diện tích |
|---|---|
| Hình bình hành | $S = a \times h$ hoặc $S = ab\sin\alpha$ |
| Hình chữ nhật | $S = a \times b$ |
| Hình thoi | $S = a \times h$ hoặc $S = \frac{1}{2}d_1 \times d_2$ |
| Hình vuông | $S = a^2$ |
| Hình thang | $S = \frac{(a+b) \times h}{2}$ |
IV. CÔNG THỨC ĐƯỜNG CHÉO HÌNH BÌNH HÀNH
1. Tính chất đường chéo
- Hình bình hành có 2 đường chéo
- Hai đường chéo cắt nhau tại trung điểm mỗi đường
- Đường chéo KHÔNG bằng nhau (trừ trường hợp hình chữ nhật)
- Đường chéo KHÔNG vuông góc (trừ trường hợp hình thoi)
2. Công thức tính độ dài đường chéo
Công thức 1: Định lý về đường chéo hình bình hành
$$d_1^2 + d_2^2 = 2(a^2 + b^2)$$
Trong đó:
- $d_1$, $d_2$: Độ dài hai đường chéo
- $a$, $b$: Độ dài hai cạnh kề
Giải thích: Đây là định lý hình bình hành (còn gọi là định lý đường trung tuyến trong tam giác)
Từ đó suy ra:
$$d_1 = \sqrt{2(a^2 + b^2) – d_2^2}$$
$$d_2 = \sqrt{2(a^2 + b^2) – d_1^2}$$
Ví dụ 8:
- Cho hình bình hành có $a = 6$ cm, $b = 8$ cm, $d_1 = 10$ cm
- Tính $d_2$:
- $d_2^2 = 2(6^2 + 8^2) – 10^2 = 2(36 + 64) – 100 = 200 – 100 = 100$
- $d_2 = \sqrt{100} = 10$ cm
- Đáp số: 10 cm
3. Công thức tính đường chéo khi biết cạnh và góc
Công thức 2: Sử dụng định lý cosin
Trong tam giác tạo bởi hai cạnh và đường chéo:
$$d_1^2 = a^2 + b^2 – 2ab\cos\alpha$$
$$d_2^2 = a^2 + b^2 – 2ab\cos(180° – \alpha) = a^2 + b^2 + 2ab\cos\alpha$$
Trong đó:
- $d_1$: Đường chéo nối hai đỉnh có góc $\alpha$
- $d_2$: Đường chéo kia
- $\alpha$: Góc giữa hai cạnh $a$ và $b$
Rút gọn:
$$d_1 = \sqrt{a^2 + b^2 – 2ab\cos\alpha}$$
$$d_2 = \sqrt{a^2 + b^2 + 2ab\cos\alpha}$$
Ví dụ 9:
- Cho hình bình hành có $a = 5$ cm, $b = 7$ cm, $\alpha = 60°$
- Tính $d_1$:
- $d_1 = \sqrt{5^2 + 7^2 – 2 \times 5 \times 7 \times \cos 60°}$
- $= \sqrt{25 + 49 – 70 \times 0.5} = \sqrt{74 – 35} = \sqrt{39}$ cm ≈ 6.24 cm
- Tính $d_2$:
- $d_2 = \sqrt{5^2 + 7^2 + 2 \times 5 \times 7 \times \cos 60°}$
- $= \sqrt{25 + 49 + 35} = \sqrt{109}$ cm ≈ 10.44 cm
- Đáp số: $d_1 = \sqrt{39}$ cm, $d_2 = \sqrt{109}$ cm
4. Công thức đường chéo trong hệ tọa độ
Công thức 3: Khi biết tọa độ các đỉnh
Cho hình bình hành ABCD với:
- $A(x_1, y_1)$, $B(x_2, y_2)$, $C(x_3, y_3)$, $D(x_4, y_4)$
Độ dài hai đường chéo:
$$AC = \sqrt{(x_3 – x_1)^2 + (y_3 – y_1)^2}$$
$$BD = \sqrt{(x_4 – x_2)^2 + (y_4 – y_2)^2}$$
Ví dụ 10:
- Cho $A(1, 2)$, $B(5, 3)$, $C(7, 6)$, $D(3, 5)$
- $AC = \sqrt{(7-1)^2 + (6-2)^2} = \sqrt{36 + 16} = \sqrt{52} = 2\sqrt{13}$
- $BD = \sqrt{(3-5)^2 + (5-3)^2} = \sqrt{4 + 4} = \sqrt{8} = 2\sqrt{2}$
- Đáp số: $AC = 2\sqrt{13}$, $BD = 2\sqrt{2}$
5. Tính góc giữa hai đường chéo
Công thức:
$$\sin\theta = \frac{2S}{d_1 \times d_2}$$
Trong đó $S$ là diện tích hình bình hành.
V. CÁC CÔNG THỨC LIÊN QUAN KHÁC
1. Công thức tính chiều cao
Công thức 1: Từ diện tích và cạnh đáy
$$h = \frac{S}{a}$$
Công thức 2: Từ cạnh bên và góc
$$h = b \times \sin\alpha$$
Trong đó:
- $b$: Cạnh bên
- $\alpha$: Góc giữa cạnh bên và cạnh đáy
Ví dụ 11:
- Cho hình bình hành có cạnh bên $b = 10$ cm, góc $\alpha = 30°$
- Chiều cao: $h = 10 \times \sin 30° = 10 \times 0.5 = 5$ cm
- Đáp số: 5 cm
2. Công thức tính góc
Công thức 1: Từ chiều cao và cạnh bên
$$\sin\alpha = \frac{h}{b}$$
$$\alpha = \arcsin\left(\frac{h}{b}\right)$$
Công thức 2: Từ đường chéo và cạnh (định lý cosin)
$$\cos\alpha = \frac{a^2 + b^2 – d_1^2}{2ab}$$
$$\alpha = \arccos\left(\frac{a^2 + b^2 – d_1^2}{2ab}\right)$$
Ví dụ 12:
- Cho hình bình hành có $a = 6$ cm, $b = 8$ cm, $d_1 = 10$ cm
- $\cos\alpha = \frac{6^2 + 8^2 – 10^2}{2 \times 6 \times 8} = \frac{36 + 64 – 100}{96} = 0$
- $\Rightarrow \alpha = 90°$ (hình chữ nhật)
- Đáp số: 90°
3. Công thức tính cạnh
Công thức 1: Từ chu vi và cạnh kia
$$b = \frac{P}{2} – a$$
Công thức 2: Từ diện tích và chiều cao
$$a = \frac{S}{h}$$
4. Bảng tổng hợp các công thức quan trọng
| Đại lượng | Công thức | Điều kiện |
|---|---|---|
| Chu vi | $P = 2(a + b)$ | Biết 2 cạnh kề |
| Diện tích | $S = a \times h$ | Biết đáy và chiều cao |
| Diện tích | $S = ab\sin\alpha$ | Biết 2 cạnh và góc |
| Diện tích | $S = \frac{1}{2}d_1 d_2 \sin\theta$ | Biết đường chéo và góc |
| Đường chéo | $d_1^2 + d_2^2 = 2(a^2 + b^2)$ | Định lý hình bình hành |
| Đường chéo | $d_1 = \sqrt{a^2 + b^2 – 2ab\cos\alpha}$ | Định lý cosin |
| Chiều cao | $h = b\sin\alpha$ | Từ cạnh bên và góc |
| Chiều cao | $h = \frac{S}{a}$ | Từ diện tích |
VI. CÁCH NHẬN BIẾT VÀ CHỨNG MINH HÌNH BÌNH HÀNH
1. Dấu hiệu nhận biết hình bình hành
Tứ giác ABCD là hình bình hành nếu thỏa mãn MỘT trong các điều kiện sau:
Dấu hiệu 1: Các cạnh đối song song
- $AB \parallel CD$ và $BC \parallel AD$
Dấu hiệu 2: Các cạnh đối bằng nhau
- $AB = CD$ và $BC = AD$
Dấu hiệu 3: Hai cạnh đối song song và bằng nhau
- $AB \parallel CD$ và $AB = CD$
Dấu hiệu 4: Các góc đối bằng nhau
- $\angle A = \angle C$ và $\angle B = \angle D$
Dấu hiệu 5: Hai đường chéo cắt nhau tại trung điểm mỗi đường
- $OA = OC$ và $OB = OD$ (O là giao điểm hai đường chéo)
2. Phương pháp chứng minh
Ví dụ chứng minh:
Cho tứ giác ABCD có $AB = CD = 5$ cm, $BC = AD = 7$ cm. Chứng minh ABCD là hình bình hành.
Chứng minh:
- Ta có: $AB = CD$ và $BC = AD$ (các cạnh đối bằng nhau)
- Theo dấu hiệu 2, ABCD là hình bình hành
3. Phân biệt hình bình hành với các hình khác
| Hình | Đặc điểm riêng |
|---|---|
| Hình bình hành | Cạnh đối song song và bằng nhau |
| Hình chữ nhật | Hình bình hành + có góc vuông |
| Hình thoi | Hình bình hành + có 2 cạnh kề bằng nhau |
| Hình vuông | Hình bình hành + góc vuông + cạnh bằng nhau |
| Hình thang | Chỉ có 1 cặp cạnh đối song song |
VII. VÍ DỤ TỔNG HỢP VÀ BÀI TẬP ÁP DỤNG
Dạng 1: Tính chu vi hình bình hành
Bài 1: Cho hình bình hành ABCD có $AB = 12$ cm, $BC = 8$ cm. Tính chu vi.
Lời giải:
- Chu vi: $P = 2(AB + BC) = 2(12 + 8) = 2 \times 20 = 40$ cm
- Đáp số: 40 cm
Bài 2: Hình bình hành có chu vi 50 cm, một cạnh dài hơn cạnh kia 5 cm. Tính độ dài mỗi cạnh.
Lời giải:
- Gọi cạnh ngắn là $a$ (cm), cạnh dài là $a + 5$ (cm)
- Chu vi: $P = 2[a + (a + 5)] = 2(2a + 5) = 4a + 10 = 50$
- $\Rightarrow 4a = 40 \Rightarrow a = 10$ cm
- Cạnh dài: $10 + 5 = 15$ cm
- Đáp số: 10 cm và 15 cm
Dạng 2: Tính diện tích hình bình hành
Bài 3: Cho hình bình hành có đáy $a = 15$ cm, chiều cao $h = 8$ cm. Tính diện tích.
Lời giải:
- Diện tích: $S = a \times h = 15 \times 8 = 120$ cm²
- Đáp số: 120 cm²
Bài 4: Cho hình bình hành có $a = 10$ cm, $b = 6$ cm, góc $\alpha = 45°$. Tính diện tích.
Lời giải:
- Diện tích: $S = ab\sin\alpha = 10 \times 6 \times \sin 45°$
- $= 60 \times \frac{\sqrt{2}}{2} = 30\sqrt{2}$ cm² $\approx 42.43$ cm²
- Đáp số: $30\sqrt{2}$ cm² ≈ 42.43 cm²
Bài 5: Hình bình hành có hai đường chéo $d_1 = 12$ cm, $d_2 = 16$ cm, góc giữa chúng $\theta = 90°$. Tính diện tích.
Lời giải:
- Diện tích: $S = \frac{1}{2}d_1 d_2 \sin\theta = \frac{1}{2} \times 12 \times 16 \times \sin 90°$
- $= \frac{1}{2} \times 12 \times 16 \times 1 = 96$ cm²
- Đáp số: 96 cm²
Dạng 3: Tính đường chéo
Bài 6: Cho hình bình hành có $a = 8$ cm, $b = 6$ cm. Biết tổng bình phương hai đường chéo bằng bao nhiêu?
Lời giải:
- Theo định lý: $d_1^2 + d_2^2 = 2(a^2 + b^2)$
- $= 2(8^2 + 6^2) = 2(64 + 36) = 2 \times 100 = 200$ cm²
- Đáp số: 200 cm²
Bài 7: Cho hình bình hành có $a = 5$ cm, $b = 7$ cm, $\alpha = 60°$. Tính độ dài hai đường chéo.
Lời giải:
- $d_1 = \sqrt{a^2 + b^2 – 2ab\cos\alpha}$
- $= \sqrt{5^2 + 7^2 – 2 \times 5 \times 7 \times 0.5}$
- $= \sqrt{25 + 49 – 35} = \sqrt{39}$ cm $\approx 6.24$ cm
- $d_2 = \sqrt{a^2 + b^2 + 2ab\cos\alpha}$
- $= \sqrt{25 + 49 + 35} = \sqrt{109}$ cm $\approx 10.44$ cm
- Đáp số: $\sqrt{39}$ cm và $\sqrt{109}$ cm
Dạng 4: Bài toán tổng hợp
Bài 8: Cho hình bình hành ABCD có diện tích 84 cm², chiều cao từ D xuống AB là 7 cm. Tính độ dài AB và chu vi biết $BC = 10$ cm.
Lời giải:
- Từ $S = AB \times h$:
- $AB = \frac{S}{h} = \frac{84}{7} = 12$ cm
- Chu vi: $P = 2(AB + BC) = 2(12 + 10) = 44$ cm
- Đáp số: AB = 12 cm, chu vi = 44 cm
Bài 9: Hình bình hành có chu vi 40 cm, diện tích 96 cm², chiều cao 8 cm. Tính độ dài mỗi cạnh.
Lời giải:
- Từ $S = a \times h$: $a = \frac{96}{8} = 12$ cm
- Từ $P = 2(a + b)$: $40 = 2(12 + b)$
- $\Rightarrow 20 = 12 + b \Rightarrow b = 8$ cm
- Đáp số: 12 cm và 8 cm
Bài 10: Cho hình bình hành ABCD có $A(1, 2)$, $B(5, 4)$, $D(2, 6)$. a) Tìm tọa độ C b) Tính chu vi c) Tính diện tích
Lời giải:
a) Vì ABCD là hình bình hành nên $\overrightarrow{AB} = \overrightarrow{DC}$
- $\overrightarrow{AB} = (4, 2)$
- Gọi $C(x, y)$ thì $\overrightarrow{DC} = (x-2, y-6) = (4, 2)$
- $\Rightarrow x = 6, y = 8$
- Vậy $C(6, 8)$
b) Tính chu vi:
- $AB = \sqrt{4^2 + 2^2} = \sqrt{20} = 2\sqrt{5}$ cm
- $AD = \sqrt{1^2 + 4^2} = \sqrt{17}$ cm
- $P = 2(2\sqrt{5} + \sqrt{17})$ cm $\approx 17.2$ cm
c) Tính diện tích:
- $S = |\overrightarrow{AB} \times \overrightarrow{AD}| = |4 \times 4 – 2 \times 1| = |16 – 2| = 14$ đơn vị diện tích
Đáp số: a) C(6, 8), b) $2(2\sqrt{5} + \sqrt{17})$ cm, c) 14 đơn vị diện tích
VIII. MẸO VÀ LƯU Ý KHI HỌC HÌNH BÌNH HÀNH
1. Các sai lầm thường gặp
❌ SAI:
- Nhầm lẫn giữa chiều cao và cạnh bên
- Tính diện tích bằng $a \times b$ (chỉ đúng với hình chữ nhật)
- Nghĩ rằng hai đường chéo bằng nhau (chỉ đúng với hình chữ nhật)
- Nghĩ rằng hai đường chéo vuông góc (chỉ đúng với hình thoi)
✅ ĐÚNG:
- Chiều cao là đoạn vuông góc từ đỉnh xuống đáy
- Diện tích = $a \times h$ hoặc $ab\sin\alpha$
- Hai đường chéo chỉ bằng nhau khi là hình chữ nhật
- Hai đường chéo chỉ vuông góc khi là hình thoi
2. Mẹo nhớ công thức
Mẹo nhớ chu vi:
- “Chu vi = 2 lần tổng hai cạnh kề”
- $P = 2(a + b)$
Mẹo nhớ diện tích:
- “Diện tích = Đáy nhân Cao”
- Hoặc “Hai cạnh nhân sin góc giữa”
- $S = a \times h = ab\sin\alpha$
Mẹo nhớ đường chéo:
- “Tổng bình phương đường chéo = 2 lần tổng bình phương cạnh”
- $d_1^2 + d_2^2 = 2(a^2 + b^2)$
3. Phương pháp giải bài tập hiệu quả
Bước 1: Vẽ hình và ghi đầy đủ dữ kiện
Bước 2: Xác định đại lượng cần tìm
Bước 3: Chọn công thức phù hợp
Bước 4: Thay số và tính toán
Bước 5: Kiểm tra đơn vị và kết quả
4. Kỹ thuật vẽ hình bình hành chuẩn
- Vẽ cạnh đáy AB nằm ngang
- Vẽ cạnh AD nghiêng (không vuông góc với AB)
- Từ D vẽ đường song song với AB
- Từ B vẽ đường song song với AD
- Hai đường này cắt nhau tại C
- Đánh dấu rõ các cạnh bằng nhau, góc bằng nhau
IX. ỨNG DỤNG THỰC TẾ CỦA HÌNH BÌNH HÀNH
1. Trong kiến trúc và xây dựng
- Mái nhà: Nhiều mái nhà có dạng hình bình hành để thoát nước tốt
- Cầu thang: Lan can cầu thang thường tạo thành các hình bình hành
- Cửa sổ: Thiết kế cửa sổ mở nghiêng dạng hình bình hành
- Gạch lát: Gạch lát nền hình bình hành tạo họa tiết đẹp
2. Trong kỹ thuật cơ khí
- Cơ cấu bản lề: Sử dụng nguyên lý hình bình hành để chuyển động
- Giàn giáo: Khung giàn giáo dạng hình bình hành chịu lực tốt
- Khung xe đạp: Một số khung xe đạp có dạng hình bình hành
- Kéo thước: Thước gấp tạo thành hình bình hành khi mở ra
3. Trong đồ chơi và giải trí
- Cánh diều: Nhiều cánh diều có khung hình bình hành
- Đồ chơi xếp hình: Các mảnh ghép hình bình hành
- Bàn bi-a: Góc đánh bi-a tạo thành hình bình hành (định luật phản xạ)
4. Trong nghệ thuật và thiết kế
- Họa tiết trang trí: Hình bình hành tạo hiệu ứng thị giác 3D
- Logo thương hiệu: Nhiều logo sử dụng hình bình hành
- Thiết kế nội thất: Gạch ốp tường, thảm trải sàn
5. Trong khoa học
- Vật lý: Quy tắc hình bình hành trong tổng hợp lực, vectơ
- Tinh thể học: Nhiều cấu trúc tinh thể có dạng hình bình hành
- Địa chất: Cấu trúc đá phiến có lớp dạng hình bình hành
X. KẾT LUẬN
Tổng kết
Bài viết đã tổng hợp đầy đủ các công thức về hình bình hành, bao gồm:
Công thức chu vi: $P = 2(a + b)$
Công thức diện tích:
- $S = a \times h$ (đáy nhân chiều cao)
- $S = ab\sin\alpha$ (hai cạnh nhân sin góc)
- $S = \frac{1}{2}d_1 d_2 \sin\theta$ (đường chéo)
Công thức đường chéo:
- $d_1^2 + d_2^2 = 2(a^2 + b^2)$
- $d_1 = \sqrt{a^2 + b^2 – 2ab\cos\alpha}$
Các công thức phụ: Chiều cao, góc, cạnh
Dấu hiệu nhận biết: 5 dấu hiệu quan trọng
Ví dụ chi tiết: 10+ bài tập có lời giải
Tầm quan trọng của hình bình hành
Trong học tập:
- Nền tảng hình học lớp 8
- Kiến thức cơ sở cho hình chữ nhật, hình thoi, hình vuông
- Ứng dụng trong vectơ, tọa độ (lớp 10)
Trong thực tế:
- Kiến trúc, xây dựng
- Kỹ thuật cơ khí
- Nghệ thuật, thiết kế
- Vật lý (quy tắc hình bình hành cho lực, vectơ)
Xem thêm các bài viết liên quan:
- Công thức hình chữ nhật – Chu vi và diện tích
- Công thức hình thoi – Đầy đủ và chi tiết
- Công thức hình vuông – Tổng hợp toàn diện
- Công thức hình thang – Các dạng bài tập
- Bài tập hình bình hành có lời giải chi tiết

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
