Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU
- 1. Trung điểm là gì?
- 2. Cấu trúc bài viết
- II. CÔNG THỨC TRUNG ĐIỂM TRÊN TRỤC SỐ
- Công thức cơ bản (1D)
- III. CÔNG THỨC TỌA ĐỘ TRUNG ĐIỂM CỦA ĐOẠN THẲNG TRONG MẶT PHẲNG (2D)
- Định nghĩa tọa độ trung điểm của đoạn thẳng
- Công thức tổng quát
- Chứng minh bằng vectơ
- Tính chất quan trọng
- Ví dụ minh họa
- Ứng dụng: Tìm tâm hình bình hành
- IV. CÔNG THỨC TRUNG ĐIỂM TRONG KHÔNG GIAN (3D)
- Công thức tổng quát
- Ví dụ minh họa
- Ứng dụng: Tìm trung điểm cạnh tứ diện
- V. CÔNG THỨC MỞ RỘNG – CHIA ĐOẠN THEO TỈ LẾ
- Công thức chia đoạn thẳng
- VI. BÀI TẬP THỰC TẾ
- Bài tập 1: Tìm điểm giữa hai thành phố
- Bài tập 2: Tìm tâm đường tròn qua 2 điểm
- Bài tập 3: Tìm điểm cân bằng của thanh
- Bài tập 4: Chia mảnh đất
- Bài tập 5: Nội suy điểm trong đồ họa
- VII. BẢNG TỔNG HỢP & MẸO NHỚ
- Bảng công thức theo chiều
- Bảng công thức liên quan
- Quy trình 3 bước
- Mẹo nhớ và lưu ý
- VIII. KẾT LUẬN
- Tổng kết
- Tài liệu tham khảo
I. GIỚI THIỆU
1. Trung điểm là gì?
Định nghĩa: Trung điểm của đoạn thẳng AB là điểm M nằm giữa A và B sao cho $MA = MB$. Nói cách khác, trung điểm chia đoạn thẳng thành hai phần có độ dài bằng nhau.
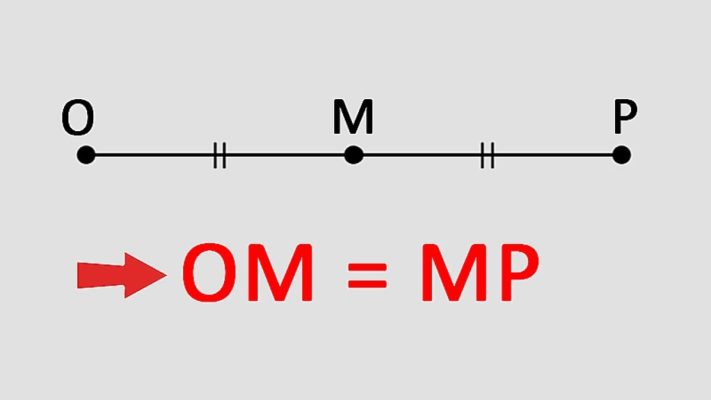
Tính chất: Trung điểm M có đặc điểm:
- Nằm trên đoạn thẳng AB
- Cách đều hai đầu mút A và B
- Chia đoạn thẳng AB thành hai phần bằng nhau
Ký hiệu: Khi M là trung điểm của AB, ta viết: $M \in AB$ và $MA = MB = \frac{AB}{2}$
2. Cấu trúc bài viết
Bài viết sẽ trình bày công thức tính tọa độ trung điểm theo độ phức tạp tăng dần:
- Công thức trên trục số (1D)
- Công thức trong mặt phẳng (2D)
- Công thức trong không gian (3D)
- Công thức mở rộng (chia đoạn theo tỉ lệ)
- 8 ví dụ minh họa chi tiết
- 5 bài tập thực tế ứng dụng
II. CÔNG THỨC TRUNG ĐIỂM TRÊN TRỤC SỐ
Công thức cơ bản (1D)
Cho hai điểm $A(x_A)$ và $B(x_B)$ trên trục số.
Trung điểm $M$ có tọa độ:
$$x_M = \frac{x_A + x_B}{2}$$
Giải thích: Tọa độ trung điểm là trung bình cộng tọa độ hai đầu mút. Đây là công thức đơn giản nhất và là nền tảng cho các công thức phức tạp hơn.
Ví dụ 1:
- Cho $A(2)$ và $B(8)$ trên trục số
- Trung điểm: $x_M = \frac{2 + 8}{2} = \frac{10}{2} = 5$
- Vậy $M(5)$
Kiểm tra: M nằm giữa A và B, cách A là 3 đơn vị, cách B cũng 3 đơn vị ✓
Ví dụ 2:
- Cho $A(-3)$ và $B(5)$
- $x_M = \frac{-3 + 5}{2} = \frac{2}{2} = 1$
- Vậy $M(1)$
Kiểm tra: M nằm giữa A và B, $MA = 1 – (-3) = 4$ và $MB = 5 – 1 = 4$ ✓
Lưu ý:
- Công thức đúng với mọi giá trị (dương, âm, phân số, số thập phân)
- Nếu $A = B$ thì trung điểm trùng với A và B
- Thứ tự A và B không quan trọng: trung điểm AB = trung điểm BA
III. CÔNG THỨC TỌA ĐỘ TRUNG ĐIỂM CỦA ĐOẠN THẲNG TRONG MẶT PHẲNG (2D)
Định nghĩa tọa độ trung điểm của đoạn thẳng
Đoạn thẳng AB: Là phần đường thẳng giới hạn bởi hai điểm A và B, bao gồm cả hai điểm đầu mút.
Trung điểm của đoạn thẳng AB: Là điểm M thuộc đoạn thẳng AB sao cho:
- M nằm giữa A và B
- $MA = MB$ (cách đều hai đầu mút)
- $AM + MB = AB$
- $AM = MB = \frac{AB}{2}$
Công thức tổng quát
Cho đoạn thẳng AB với hai đầu mút trong mặt phẳng Oxy:
- $A(x_A; y_A)$
- $B(x_B; y_B)$
Trung điểm $M(x_M; y_M)$ của đoạn thẳng AB có tọa độ:
$$\boxed{x_M = \frac{x_A + x_B}{2}, \quad y_M = \frac{y_A + y_B}{2}}$$
Hoặc viết gọn:
$$M\left(\frac{x_A + x_B}{2}; \frac{y_A + y_B}{2}\right)$$
Cách nhớ: “Trung bình cộng hoành độ, trung bình cộng tung độ”
Chứng minh bằng vectơ
Điều kiện M là trung điểm AB: $$\overrightarrow{MA} + \overrightarrow{MB} = \vec{0}$$
Hay: $$\overrightarrow{OM} = \frac{\overrightarrow{OA} + \overrightarrow{OB}}{2}$$
Với O là gốc tọa độ, ta có:
- $\overrightarrow{OA} = (x_A; y_A)$
- $\overrightarrow{OB} = (x_B; y_B)$
- $\overrightarrow{OM} = (x_M; y_M)$
Từ đó: $$x_M = \frac{x_A + x_B}{2}, \quad y_M = \frac{y_A + y_B}{2}$$
Tính chất quan trọng
Tính chất 1: Độ dài đoạn thẳng từ đầu mút đến trung điểm $$AM = MB = \frac{1}{2}AB$$
Tính chất 2: Tọa độ trung điểm nằm giữa hai đầu mút
- Nếu $x_A < x_B$ thì $x_A < x_M < x_B$
- Nếu $y_A < y_B$ thì $y_A < y_M < y_B$
Tính chất 3: Trung điểm chia vector thành hai vector bằng nhau ngược hướng $$\overrightarrow{MA} = -\overrightarrow{MB}$$
Ví dụ minh họa
Ví dụ 3: Tìm trung điểm của $A(1; 3)$ và $B(5; 7)$
Lời giải:
- $x_M = \frac{1 + 5}{2} = \frac{6}{2} = 3$
- $y_M = \frac{3 + 7}{2} = \frac{10}{2} = 5$
- Vậy $M(3; 5)$
Kiểm tra:
- $MA = \sqrt{(3-1)^2 + (5-3)^2} = \sqrt{4+4} = 2\sqrt{2}$
- $MB = \sqrt{(5-3)^2 + (7-5)^2} = \sqrt{4+4} = 2\sqrt{2}$
- $MA = MB$ ✓
Ví dụ 4: Tìm trung điểm của $A(-2; 4)$ và $B(6; -2)$
Lời giải:
- $x_M = \frac{-2 + 6}{2} = \frac{4}{2} = 2$
- $y_M = \frac{4 + (-2)}{2} = \frac{2}{2} = 1$
- Vậy $M(2; 1)$
Ví dụ 5 (Bài toán ngược): Cho $A(2; 5)$ và trung điểm $M(4; 3)$. Tìm tọa độ điểm $B$.
Lời giải:
- Từ công thức: $x_M = \frac{x_A + x_B}{2}$
- $\Rightarrow 4 = \frac{2 + x_B}{2}$
- $\Rightarrow 8 = 2 + x_B$
- $\Rightarrow x_B = 6$
- Tương tự: $3 = \frac{5 + y_B}{2}$
- $\Rightarrow 6 = 5 + y_B$
- $\Rightarrow y_B = 1$
- Vậy $B(6; 1)$
Công thức tổng quát cho bài toán ngược: $$\boxed{x_B = 2x_M – x_A, \quad y_B = 2y_M – y_A}$$
Ứng dụng: Tìm tâm hình bình hành
Trong hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại trung điểm mỗi đường.
Bài toán: Cho hình bình hành ABCD với $A(1; 2)$, $B(4; 3)$, $C(6; 5)$. Tìm $D$.
Lời giải:
- Gọi $O$ là giao điểm hai đường chéo
- $O$ là trung điểm AC:
- $x_O = \frac{1+6}{2} = \frac{7}{2}$
- $y_O = \frac{2+5}{2} = \frac{7}{2}$
- $O\left(\frac{7}{2}; \frac{7}{2}\right)$
- $O$ cũng là trung điểm BD, áp dụng công thức ngược:
- $x_D = 2 \times \frac{7}{2} – 4 = 7 – 4 = 3$
- $y_D = 2 \times \frac{7}{2} – 3 = 7 – 3 = 4$
- Vậy $D(3; 4)$
Kiểm tra: $\overrightarrow{AB} = (3; 1)$ và $\overrightarrow{DC} = (3; 1)$ → $\overrightarrow{AB} = \overrightarrow{DC}$ ✓
IV. CÔNG THỨC TRUNG ĐIỂM TRONG KHÔNG GIAN (3D)
Công thức tổng quát
Cho hai điểm trong không gian Oxyz:
- $A(x_A; y_A; z_A)$
- $B(x_B; y_B; z_B)$
Trung điểm $M(x_M; y_M; z_M)$ có tọa độ:
$$\boxed{x_M = \frac{x_A + x_B}{2}, \quad y_M = \frac{y_A + y_B}{2}, \quad z_M = \frac{z_A + z_B}{2}}$$
Hoặc:
$$M\left(\frac{x_A + x_B}{2}; \frac{y_A + y_B}{2}; \frac{z_A + z_B}{2}\right)$$
Nguyên tắc: Tương tự 2D, chỉ thêm tọa độ z. Áp dụng công thức trung bình cộng cho cả ba tọa độ x, y, z.
Ví dụ minh họa
Ví dụ 6: Tìm trung điểm của $A(1; 2; 3)$ và $B(5; 4; -1)$
Lời giải:
- $x_M = \frac{1 + 5}{2} = \frac{6}{2} = 3$
- $y_M = \frac{2 + 4}{2} = \frac{6}{2} = 3$
- $z_M = \frac{3 + (-1)}{2} = \frac{2}{2} = 1$
- Vậy $M(3; 3; 1)$
Kiểm tra:
- $MA = \sqrt{(3-1)^2 + (3-2)^2 + (1-3)^2} = \sqrt{4+1+4} = 3$
- $MB = \sqrt{(5-3)^2 + (4-3)^2 + (-1-1)^2} = \sqrt{4+1+4} = 3$
- $MA = MB$ ✓
Ví dụ 7 (Bài toán ngược): Cho $A(2; -1; 3)$ và trung điểm $M(4; 1; 0)$. Tìm $B$.
Lời giải:
- $x_B = 2 \times 4 – 2 = 8 – 2 = 6$
- $y_B = 2 \times 1 – (-1) = 2 + 1 = 3$
- $z_B = 2 \times 0 – 3 = 0 – 3 = -3$
- Vậy $B(6; 3; -3)$
Công thức tổng quát cho bài toán ngược 3D: $$\boxed{x_B = 2x_M – x_A, \quad y_B = 2y_M – y_A, \quad z_B = 2z_M – z_A}$$
Ứng dụng: Tìm trung điểm cạnh tứ diện
Bài toán: Cho tứ diện ABCD với $A(1; 0; 0)$, $B(0; 1; 0)$, $C(0; 0; 1)$, $D(1; 1; 1)$. Tìm trung điểm các cạnh.
Lời giải:
Trung điểm AB:
- $M_{AB}\left(\frac{1+0}{2}; \frac{0+1}{2}; \frac{0+0}{2}\right) = \left(\frac{1}{2}; \frac{1}{2}; 0\right)$
Trung điểm AC:
- $M_{AC}\left(\frac{1+0}{2}; \frac{0+0}{2}; \frac{0+1}{2}\right) = \left(\frac{1}{2}; 0; \frac{1}{2}\right)$
Trung điểm AD:
- $M_{AD}\left(\frac{1+1}{2}; \frac{0+1}{2}; \frac{0+1}{2}\right) = \left(1; \frac{1}{2}; \frac{1}{2}\right)$
Trung điểm BC:
- $M_{BC}\left(\frac{0+0}{2}; \frac{1+0}{2}; \frac{0+1}{2}\right) = \left(0; \frac{1}{2}; \frac{1}{2}\right)$
Trung điểm BD:
- $M_{BD}\left(\frac{0+1}{2}; \frac{1+1}{2}; \frac{0+1}{2}\right) = \left(\frac{1}{2}; 1; \frac{1}{2}\right)$
Trung điểm CD:
- $M_{CD}\left(\frac{0+1}{2}; \frac{0+1}{2}; \frac{1+1}{2}\right) = \left(\frac{1}{2}; \frac{1}{2}; 1\right)$
V. CÔNG THỨC MỞ RỘNG – CHIA ĐOẠN THEO TỈ LẾ
Công thức chia đoạn thẳng
Cho đoạn thẳng AB và điểm M chia đoạn AB theo tỉ lệ $k$ (tức $\frac{MA}{MB} = k$)
Công thức trong mặt phẳng:
$$x_M = \frac{x_A + k \cdot x_B}{1 + k}, \quad y_M = \frac{y_A + k \cdot y_B}{1 + k}$$
Công thức trong không gian:
$$x_M = \frac{x_A + k \cdot x_B}{1 + k}, \quad y_M = \frac{y_A + k \cdot y_B}{1 + k}, \quad z_M = \frac{z_A + k \cdot z_B}{1 + k}$$
Trường hợp đặc biệt:
- Nếu $k = 1$ (chia đôi): M là trung điểm → Công thức trung điểm thông thường
- Nếu $k = 2$: M chia AB theo tỉ lệ 2:1 (M gần B hơn, cách A gấp đôi cách B)
- Nếu $k = \frac{1}{2}$: M chia AB theo tỉ lệ 1:2 (M gần A hơn, cách B gấp đôi cách A)
Ví dụ 8: Cho $A(0; 0)$ và $B(6; 4)$. Tìm M chia AB theo tỉ lệ 2:1 (M gần B hơn).
Lời giải:
- $k = 2$ (vì $\frac{MA}{MB} = \frac{2}{1} = 2$)
- $x_M = \frac{0 + 2 \times 6}{1 + 2} = \frac{0 + 12}{3} = \frac{12}{3} = 4$
- $y_M = \frac{0 + 2 \times 4}{1 + 2} = \frac{0 + 8}{3} = \frac{8}{3}$
- Vậy $M\left(4; \frac{8}{3}\right)$
Kiểm tra:
- $MA = \sqrt{16 + \frac{64}{9}} = \sqrt{\frac{144 + 64}{9}} = \sqrt{\frac{208}{9}} = \frac{4\sqrt{13}}{3}$
- $MB = \sqrt{4 + \frac{16}{9}} = \sqrt{\frac{36 + 16}{9}} = \sqrt{\frac{52}{9}} = \frac{2\sqrt{13}}{3}$
- $\frac{MA}{MB} = \frac{4\sqrt{13}/3}{2\sqrt{13}/3} = \frac{4}{2} = 2$ ✓
Lưu ý quan trọng:
- Khi $k = 1$: $M = \frac{A + B}{2}$ (trung điểm)
- Khi $k = 0$: M trùng với A
- Khi $k \to \infty$: M tiến đến B
VI. BÀI TẬP THỰC TẾ
Bài tập 1: Tìm điểm giữa hai thành phố
Đề bài: Trên bản đồ, thành phố A có tọa độ (10; 20) km, thành phố B có tọa độ (50; 60) km. Cần đặt trạm dừng chân tại trung điểm giữa hai thành phố. Tìm vị trí trạm.
Lời giải:
Áp dụng công thức trung điểm:
- $x_M = \frac{10 + 50}{2} = \frac{60}{2} = 30$ km
- $y_M = \frac{20 + 60}{2} = \frac{80}{2} = 40$ km
Kết luận: Trạm dừng chân nên đặt tại tọa độ $(30; 40)$ km trên bản đồ.
Kiểm tra khoảng cách:
- Khoảng cách từ A đến M: $\sqrt{(30-10)^2 + (40-20)^2} = \sqrt{400 + 400} = 20\sqrt{2} \approx 28,28$ km
- Khoảng cách từ B đến M: $\sqrt{(50-30)^2 + (60-40)^2} = \sqrt{400 + 400} = 20\sqrt{2} \approx 28,28$ km
- Hai khoảng cách bằng nhau ✓
Ứng dụng thực tế: Quy hoạch giao thông, đặt trạm xăng, trạm sạc xe điện, khu nghỉ chân trên đường cao tốc.
Bài tập 2: Tìm tâm đường tròn qua 2 điểm
Đề bài: Đường tròn có đường kính AB với $A(2; 3)$, $B(8; 7)$. Tìm tâm và bán kính đường tròn.
Lời giải:
Bước 1: Tâm I là trung điểm của đường kính AB
- $x_I = \frac{2 + 8}{2} = \frac{10}{2} = 5$
- $y_I = \frac{3 + 7}{2} = \frac{10}{2} = 5$
- Vậy $I(5; 5)$
Bước 2: Tính bán kính
- Độ dài AB: $AB = \sqrt{(8-2)^2 + (7-3)^2} = \sqrt{36 + 16} = \sqrt{52} = 2\sqrt{13}$
- Bán kính: $R = \frac{AB}{2} = \frac{2\sqrt{13}}{2} = \sqrt{13} \approx 3,61$
Kết luận: Đường tròn có tâm $I(5; 5)$ và bán kính $R = \sqrt{13}$ đơn vị.
Phương trình đường tròn: $(x – 5)^2 + (y – 5)^2 = 13$
Ứng dụng: Vẽ đường tròn trong thiết kế đồ họa, kiến trúc, tìm quỹ đạo chuyển động tròn.
Bài tập 3: Tìm điểm cân bằng của thanh
Đề bài: Thanh kim loại đồng chất có hai đầu tại $A(0; 0; 0)$ m và $B(4; 2; 6)$ m trong không gian. Tìm trọng tâm (điểm cân bằng) của thanh.
Lời giải:
Đối với vật thể đồng chất, trọng tâm nằm tại trung điểm:
- $x_G = \frac{0 + 4}{2} = 2$ m
- $y_G = \frac{0 + 2}{2} = 1$ m
- $z_G = \frac{0 + 6}{2} = 3$ m
Kết luận: Trọng tâm (điểm cân bằng) của thanh ở vị trí $G(2; 1; 3)$ m.
Giải thích vật lý: Nếu đặt thanh trên giá đỡ tại điểm G, thanh sẽ nằm cân bằng ngang. Khoảng cách từ G đến A bằng khoảng cách từ G đến B:
$$GA = GB = \sqrt{4 + 1 + 9} = \sqrt{14} \approx 3,74 \text{ m}$$
Ứng dụng: Cơ học, tính toán kết cấu, thiết kế cầu trục, giàn giáo, xác định điểm treo vật thể.
Bài tập 4: Chia mảnh đất
Đề bài: Mảnh đất hình chữ nhật có 4 góc: $A(0; 0)$, $B(40; 0)$, $C(40; 30)$, $D(0; 30)$ (đơn vị: mét). Muốn chia làm 4 phần bằng nhau bằng hai đường thẳng song song với các cạnh và vuông góc với nhau. Tìm tọa độ điểm giao của hai đường chia.
Lời giải:
Phương pháp: Điểm giao O của hai đường chia là trung điểm của đường chéo AC (hoặc BD).
Cách 1: Dùng đường chéo AC
- $x_O = \frac{0 + 40}{2} = 20$ m
- $y_O = \frac{0 + 30}{2} = 15$ m
Cách 2: Dùng đường chéo BD (kiểm tra)
- $x_O = \frac{40 + 0}{2} = 20$ m
- $y_O = \frac{0 + 30}{2} = 15$ m
Kết luận: Điểm giao O nằm tại tọa độ $(20; 15)$ m.
Phân chia: Hai đường chia là:
- Đường thẳng đứng: $x = 20$ (song song Oy)
- Đường nằm ngang: $y = 15$ (song song Ox)
Bốn phần đất có diện tích bằng nhau, mỗi phần: $\frac{40 \times 30}{4} = 300$ m²
Ứng dụng: Quy hoạch đất, chia tách thửa, thiết kế khu đô thị, phân lô bán nền.
Bài tập 5: Nội suy điểm trong đồ họa
Đề bài: Trong animation, một vật di chuyển từ điểm $A(100; 200)$ px đến điểm $B(500; 400)$ px. Tìm vị trí của vật tại thời điểm giữa hành trình (50% quãng đường).
Lời giải:
Vị trí tại 50% hành trình chính là trung điểm:
- $x_M = \frac{100 + 500}{2} = \frac{600}{2} = 300$ px
- $y_M = \frac{200 + 400}{2} = \frac{600}{2} = 300$ px
Kết luận: Vật ở vị trí $M(300; 300)$ px tại thời điểm giữa.
Mở rộng – Nội suy tuyến tính (Linear Interpolation):
Tại thời điểm $t$ (với $0 \le t \le 1$): $$x(t) = x_A + t(x_B – x_A) = 100 + t \times 400$$ $$y(t) = y_A + t(y_B – y_A) = 200 + t \times 200$$
Ví dụ:
- Tại $t = 0$ (bắt đầu): $(100; 200)$ ← điểm A
- Tại $t = 0,25$ (25%): $(200; 250)$
- Tại $t = 0,5$ (50%): $(300; 300)$ ← trung điểm M
- Tại $t = 0,75$ (75%): $(400; 350)$
- Tại $t = 1$ (kết thúc): $(500; 400)$ ← điểm B
Ứng dụng: Animation 2D/3D, game development, chuyển động mượt mà, tweening, motion graphics, UI/UX transitions.
VII. BẢNG TỔNG HỢP & MẸO NHỚ
Bảng công thức theo chiều
| Chiều | Công thức | Số tọa độ |
|---|---|---|
| 1D (trục số) | $x_M = \frac{x_A + x_B}{2}$ | 1 |
| 2D (mặt phẳng) | $x_M = \frac{x_A + x_B}{2}, \quad y_M = \frac{y_A + y_B}{2}$ | 2 |
| 3D (không gian) | $x_M = \frac{x_A + x_B}{2}, \quad y_M = \frac{y_A + y_B}{2}, \quad z_M = \frac{z_A + z_B}{2}$ | 3 |
Bảng công thức liên quan
| Bài toán | Công thức |
|---|---|
| Tìm trung điểm M của AB | $M = \frac{A + B}{2}$ (theo từng tọa độ) |
| Tìm B khi biết A và M | $B = 2M – A$ (theo từng tọa độ) |
| Chia đoạn theo tỉ lệ k | $M = \frac{A + kB}{1 + k}$ |
| Trọng tâm tam giác ABC | $G = \frac{A + B + C}{3}$ |
| Trọng tâm tứ giác ABCD | $G = \frac{A + B + C + D}{4}$ |
Quy trình 3 bước
Bước 1: Xác định tọa độ
- Ghi rõ tọa độ điểm A
- Ghi rõ tọa độ điểm B
- Xác định số chiều (1D, 2D hay 3D)
Bước 2: Áp dụng công thức
- Tính trung bình cộng từng tọa độ
- $x_M = \frac{x_A + x_B}{2}$
- $y_M = \frac{y_A + y_B}{2}$
- $z_M = \frac{z_A + z_B}{2}$ (nếu có)
Bước 3: Viết kết quả
- Ghi tọa độ trung điểm M
- Kiểm tra lại kết quả (nếu cần)
Mẹo nhớ và lưu ý
Mẹo 1: Khẩu quyết
“Cộng rồi chia đôi, từng tọa độ một thôi”
Mẹo 2: Kiểm tra nhanh
- Trung điểm phải nằm giữa hai đầu mút
- Nếu $x_A < x_B$ thì $x_A < x_M < x_B$
- Nếu $y_A < y_B$ thì $y_A < y_M < y_B$
Mẹo 3: Bài toán ngược
- Nhân đôi trung điểm rồi trừ điểm đã biết
- $B = 2M – A$
- Hoặc: $A = 2M – B$
Mẹo 4: Nhớ theo “trung bình”
- Trung điểm = Trung bình cộng
- Giống như điểm trung bình của 2 số
Lưu ý quan trọng:
Áp dụng công thức cho TỪNG tọa độ riêng biệt – không được cộng chéo hay nhầm lẫn các tọa độ
Không nhầm lẫn với công thức khoảng cách – công thức khoảng cách có dấu căn và bình phương
Trong 3D, nhớ cả tọa độ z – đừng quên tọa độ thứ ba
Đơn vị của M giống đơn vị của A và B – nếu A, B tính bằng mét thì M cũng bằng mét
Thứ tự A và B không quan trọng – trung điểm AB = trung điểm BA
Dấu âm cần cẩn thận – khi cộng số âm, chú ý dấu: $\frac{-3 + 5}{2} = \frac{2}{2} = 1$
VIII. KẾT LUẬN
Tổng kết
Bài viết đã trình bày đầy đủ và chi tiết công thức tính tọa độ trung điểm từ cơ bản đến nâng cao:
Công thức cốt lõi: $$M = \left(\frac{x_A + x_B}{2}; \frac{y_A + y_B}{2}; \frac{z_A + z_B}{2}\right)$$
Áp dụng đa dạng:
- Trục số (1D) – đơn giản nhất
- Mặt phẳng (2D) – phổ biến nhất
- Không gian (3D) – mở rộng tự nhiên
Công thức mở rộng:
- Chia đoạn theo tỉ lệ bất kỳ
- Bài toán ngược tìm điểm đầu mút
Ví dụ phong phú:
- 8 ví dụ lý thuyết có lời giải chi tiết
- 5 bài tập thực tế ứng dụng đa lĩnh vực
Ứng dụng thực tiễn:
- Giao thông và quy hoạch
- Hình học và thiết kế
- Vật lý và cơ học
- Đồ họa và animation
- Kiến trúc và xây dựng
Tài liệu tham khảo
Xem thêm các chủ đề liên quan:
- Công thức khoảng cách giữa hai điểm
- Công thức trọng tâm tam giác và đa giác
- Hệ tọa độ trong mặt phẳng và không gian
- Phương trình đường thẳng đi qua hai điểm
- Vector trong mặt phẳng và không gian
- Chia đoạn thẳng theo tỉ lệ cho trước

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
