Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ HÌNH LẬP PHƯƠNG
- 1. Hình lập phương là gì?
- 2. Đặc điểm nhận biết
- 3. Phân biệt hình lập phương và hình hộp chữ nhật
- II. CÔNG THỨC TÍNH THỂ TÍCH HÌNH LẬP PHƯƠNG
- 1. Công thức cơ bản
- 2. Công thức tính ngược (tìm cạnh khi biết thể tích)
- 3. Công thức thể tích theo diện tích đáy
- 4. Bảng thể tích các số lập phương thường gặp
- III. CÔNG THỨC TÍNH DIỆN TÍCH HÌNH LẬP PHƯƠNG
- 1. Diện tích một mặt (hình vuông)
- 2. Diện tích xung quanh
- 3. Diện tích toàn phần
- 4. Công thức tính cạnh khi biết diện tích
- 5. Bảng tổng hợp diện tích theo cạnh
- IV. CÔNG THỨC TÍNH ĐƯỜNG CHÉO HÌNH LẬP PHƯƠNG
- 1. Đường chéo mặt (đường chéo của hình vuông)
- 2. Đường chéo khối (đường chéo trong không gian)
- 3. Công thức tìm cạnh khi biết đường chéo
- 4. Bảng tổng hợp đường chéo theo cạnh
- V. BẢNG TỔNG HỢP TẤT CẢ CÔNG THỨC
- Bảng công thức đầy đủ hình lập phương
- Công thức tính ngược (tìm cạnh $a$)
- VI. VÍ DỤ MINH HỌA CHI TIẾT
- Dạng 1: Tính thể tích khi biết cạnh
- Dạng 2: Tính cạnh khi biết thể tích
- Dạng 3: Tính diện tích toàn phần và xung quanh
- Dạng 4: Tính cạnh khi biết diện tích
- Dạng 5: Tính đường chéo
- Dạng 6: Bài toán thực tế
- VII. MỐI LIÊN HỆ GIỮA CÁC CÔNG THỨC
- 1. Mối quan hệ giữa thể tích và diện tích
- 2. Quy luật tăng kích thước
- 3. So sánh với hình hộp chữ nhật
- VIII. CÁC SAI LẦM THƯỜNG GẶP
- 1. Nhầm lẫn công thức thể tích và diện tích
- 2. Nhầm đường chéo mặt và đường chéo khối
- 3. Quên lũy thừa (bình phương hoặc lập phương)
- 4. Nhầm lẫn đơn vị
- 5. Tính sai căn bậc ba
- IX. MẸO VÀ KỸ THUẬT NHỚ CÔNG THỨC
- 1. Mẹo nhớ công thức thể tích và diện tích
- 2. Mẹo nhớ công thức đường chéo
- 3. Học thuộc bảng lập phương
- 4. Kiểm tra nhanh kết quả
- X. ỨNG DỤNG THỰC TẾ
- 4. Trong khoa học
- XI. KẾT LUẬN
- Tổng kết công thức quan trọng nhất
I. GIỚI THIỆU VỀ HÌNH LẬP PHƯƠNG
1. Hình lập phương là gì?
Định nghĩa: Hình lập phương là một khối đa diện đều có 6 mặt đều là hình vuông bằng nhau. Đây là một trong những hình khối đơn giản và đối xứng nhất trong hình học không gian.
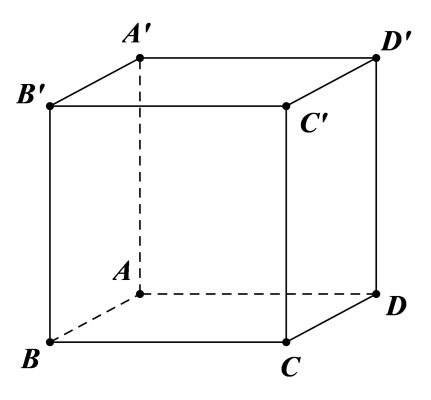
Tên gọi khác:
- Khối lập phương
- Hình vuông khối
- Cube (tiếng Anh)
- Hexahedron (thuật ngữ hình học)
Đặc điểm đặc trưng: Tất cả các kích thước (chiều dài, chiều rộng, chiều cao) đều bằng nhau và bằng độ dài cạnh $a$.
2. Đặc điểm nhận biết
Số mặt: 6 mặt
- Tất cả đều là hình vuông
- Tất cả đều bằng nhau
- Diện tích mỗi mặt: $a^2$
Số cạnh: 12 cạnh
- Tất cả đều bằng nhau
- Mỗi cạnh có độ dài $a$
- Chia thành 3 nhóm cạnh song song (4 cạnh mỗi nhóm)
Số đỉnh: 8 đỉnh
- Mỗi đỉnh là giao điểm của 3 cạnh
- Mỗi đỉnh là giao điểm của 3 mặt
- Tất cả các đỉnh đều giống nhau
Các góc:
- Tất cả các góc đều là góc vuông (90°)
- Góc giữa hai mặt: 90°
- Góc giữa hai cạnh tại đỉnh: 90°
Tính chất đối xứng:
- Có 13 trục đối xứng
- Có 9 mặt phẳng đối xứng
- Tâm đối xứng: tâm của khối lập phương
3. Phân biệt hình lập phương và hình hộp chữ nhật
| Đặc điểm | Hình lập phương | Hình hộp chữ nhật |
|---|---|---|
| Số cạnh bằng nhau | 12 cạnh bằng nhau | 3 nhóm cạnh (có thể khác nhau) |
| Các mặt | 6 hình vuông | 6 hình chữ nhật |
| Kích thước | $a = b = c$ | $a$, $b$, $c$ bất kỳ |
| Công thức thể tích | $V = a^3$ | $V = a \times b \times c$ |
| Công thức diện tích | $S_{tp} = 6a^2$ | $S_{tp} = 2(ab+bc+ca)$ |
| Quan hệ | Trường hợp đặc biệt | Dạng tổng quát |
Kết luận quan trọng: Hình lập phương là trường hợp đặc biệt của hình hộp chữ nhật khi cả ba kích thước bằng nhau ($a = b = c$). Do đó, mọi công thức của hình hộp chữ nhật đều áp dụng được cho hình lập phương.
II. CÔNG THỨC TÍNH THỂ TÍCH HÌNH LẬP PHƯƠNG
1. Công thức cơ bản
Công thức chính:
$$\boxed{V = a^3}$$
Hoặc dạng khai triển:
$$V = a \times a \times a$$
Trong đó:
- $V$: Thể tích hình lập phương
- $a$: Độ dài cạnh hình lập phương
- Đơn vị: m³, cm³, dm³, mm³…
Cách đọc:
- “Thể tích bằng cạnh lập phương”
- “Thể tích bằng a mũ ba”
- “V bằng a mũ 3”
Ý nghĩa: Thể tích hình lập phương bằng lập phương độ dài cạnh của nó.
Ví dụ đơn giản: Hình lập phương có cạnh 5 cm.
- Thể tích: $V = 5^3 = 5 \times 5 \times 5 = 125$ cm³
2. Công thức tính ngược (tìm cạnh khi biết thể tích)
Từ công thức $V = a^3$, ta có thể tìm cạnh $a$ khi biết thể tích $V$:
$$\boxed{a = \sqrt[3]{V}}$$
Trong đó: $\sqrt[3]{V}$ là căn bậc ba của thể tích.
Cách tính:
- Dùng máy tính: Nhấn phím $\sqrt[x]{y}$ hoặc $x^{1/3}$
- Hoặc nhận biết số lập phương thông dụng
Ví dụ:
- Biết $V = 64$ cm³ → $a = \sqrt[3]{64} = 4$ cm (vì $4^3 = 64$)
- Biết $V = 125$ cm³ → $a = \sqrt[3]{125} = 5$ cm (vì $5^3 = 125$)
- Biết $V = 1000$ cm³ → $a = \sqrt[3]{1000} = 10$ cm (vì $10^3 = 1000$)
3. Công thức thể tích theo diện tích đáy
Hình lập phương cũng là một lăng trụ đứng, nên áp dụng được công thức:
$$V = S_{đáy} \times h$$
Với hình lập phương:
- Diện tích đáy: $S_{đáy} = a^2$ (hình vuông cạnh $a$)
- Chiều cao: $h = a$
- Thể tích: $V = a^2 \times a = a^3$
→ Quay lại công thức cơ bản!
4. Bảng thể tích các số lập phương thường gặp
| Cạnh ($a$) | Tính toán | Thể tích ($V = a^3$) |
|---|---|---|
| 1 | $1^3$ | 1 |
| 2 | $2^3 = 2 \times 2 \times 2$ | 8 |
| 3 | $3^3 = 3 \times 3 \times 3$ | 27 |
| 4 | $4^3 = 4 \times 4 \times 4$ | 64 |
| 5 | $5^3 = 5 \times 5 \times 5$ | 125 |
| 6 | $6^3 = 6 \times 6 \times 6$ | 216 |
| 7 | $7^3 = 7 \times 7 \times 7$ | 343 |
| 8 | $8^3 = 8 \times 8 \times 8$ | 512 |
| 9 | $9^3 = 9 \times 9 \times 9$ | 729 |
| 10 | $10^3 = 10 \times 10 \times 10$ | 1000 |
Mẹo nhớ:
- Học thuộc bảng này giúp tính toán nhanh trong bài thi
- Đặc biệt nhớ: $10^3 = 1000$ (dễ nhớ nhất)
- Số 125, 216, 343, 512, 729 xuất hiện nhiều trong đề thi
Ứng dụng: Khi thấy thể tích là 216 cm³, nhận biết ngay cạnh là 6 cm.
III. CÔNG THỨC TÍNH DIỆN TÍCH HÌNH LẬP PHƯƠNG
1. Diện tích một mặt (hình vuông)
Mỗi mặt của hình lập phương là một hình vuông cạnh $a$.
$$\boxed{S_{mặt} = a^2}$$
Đơn vị: m², cm², dm², mm²
Ví dụ: Hình lập phương cạnh 4 cm có diện tích một mặt:
- $S_{mặt} = 4^2 = 16$ cm²
2. Diện tích xung quanh
Diện tích xung quanh là tổng diện tích của 4 mặt bên (không tính hai mặt đáy).
$$\boxed{S_{xq} = 4a^2}$$
Giải thích:
- Có 4 mặt bên
- Mỗi mặt có diện tích $a^2$
- Tổng: $4 \times a^2 = 4a^2$
Cách nhớ: “4 mặt bên, mỗi mặt $a^2$”
Ví dụ: Hình lập phương cạnh 5 cm:
- $S_{xq} = 4 \times 5^2 = 4 \times 25 = 100$ cm²
3. Diện tích toàn phần
Diện tích toàn phần là tổng diện tích của cả 6 mặt.
$$\boxed{S_{tp} = 6a^2}$$
Giải thích:
- Có 6 mặt (trên, dưới, trước, sau, trái, phải)
- Mỗi mặt có diện tích $a^2$
- Tổng: $6 \times a^2 = 6a^2$
Công thức mở rộng: $$S_{tp} = S_{xq} + 2S_{đáy} = 4a^2 + 2a^2 = 6a^2$$
Cách nhớ: “6 mặt vuông, mỗi mặt $a^2$”
Ví dụ: Hình lập phương cạnh 3 cm:
- $S_{tp} = 6 \times 3^2 = 6 \times 9 = 54$ cm²
4. Công thức tính cạnh khi biết diện tích
a) Biết diện tích một mặt:
Từ $S_{mặt} = a^2$, suy ra: $$\boxed{a = \sqrt{S_{mặt}}}$$
Ví dụ: Một mặt có diện tích 36 cm²
- $a = \sqrt{36} = 6$ cm
b) Biết diện tích xung quanh:
Từ $S_{xq} = 4a^2$, suy ra: $$\boxed{a = \sqrt{\frac{S_{xq}}{4}}}$$
Ví dụ: Diện tích xung quanh 64 cm²
- $a = \sqrt{\frac{64}{4}} = \sqrt{16} = 4$ cm
c) Biết diện tích toàn phần:
Từ $S_{tp} = 6a^2$, suy ra: $$\boxed{a = \sqrt{\frac{S_{tp}}{6}}}$$
Ví dụ: Diện tích toàn phần 150 cm²
- $a = \sqrt{\frac{150}{6}} = \sqrt{25} = 5$ cm
5. Bảng tổng hợp diện tích theo cạnh
| Cạnh | 1 mặt ($a^2$) | Xung quanh ($4a^2$) | Toàn phần ($6a^2$) |
|---|---|---|---|
| 1 cm | 1 cm² | 4 cm² | 6 cm² |
| 2 cm | 4 cm² | 16 cm² | 24 cm² |
| 3 cm | 9 cm² | 36 cm² | 54 cm² |
| 4 cm | 16 cm² | 64 cm² | 96 cm² |
| 5 cm | 25 cm² | 100 cm² | 150 cm² |
| 6 cm | 36 cm² | 144 cm² | 216 cm² |
| 7 cm | 49 cm² | 196 cm² | 294 cm² |
| 8 cm | 64 cm² | 256 cm² | 384 cm² |
| 9 cm | 81 cm² | 324 cm² | 486 cm² |
| 10 cm | 100 cm² | 400 cm² | 600 cm² |
Ứng dụng: Bảng này giúp kiểm tra nhanh kết quả tính toán.
IV. CÔNG THỨC TÍNH ĐƯỜNG CHÉO HÌNH LẬP PHƯƠNG
Hình lập phương có hai loại đường chéo:
1. Đường chéo mặt (đường chéo của hình vuông)
Định nghĩa: Đường chéo mặt là đoạn thẳng nối hai đỉnh đối diện trên cùng một mặt hình vuông.
Công thức:
$$\boxed{d_{mặt} = a\sqrt{2}}$$
Chứng minh: Áp dụng định lý Pythagore cho tam giác vuông có hai cạnh góc vuông bằng $a$:
- $d_{mặt}^2 = a^2 + a^2 = 2a^2$
- $d_{mặt} = \sqrt{2a^2} = a\sqrt{2}$
Giá trị xấp xỉ: $d_{mặt} \approx 1.414a$
Ví dụ: Hình lập phương cạnh 4 cm:
- $d_{mặt} = 4\sqrt{2} \approx 4 \times 1.414 = 5.66$ cm
2. Đường chéo khối (đường chéo trong không gian)
Định nghĩa: Đường chéo khối là đoạn thẳng nối hai đỉnh đối diện của khối lập phương (không cùng nằm trên một mặt).
Công thức:
$$\boxed{d_{khối} = a\sqrt{3}}$$
Chứng minh: Áp dụng định lý Pythagore trong không gian 3 chiều:
- Xét tam giác vuông trong không gian có:
- Một cạnh góc vuông: $a$ (cạnh đứng)
- Cạnh góc vuông còn lại: $a\sqrt{2}$ (đường chéo mặt đáy)
- $d_{khối}^2 = a^2 + (a\sqrt{2})^2 = a^2 + 2a^2 = 3a^2$
- $d_{khối} = \sqrt{3a^2} = a\sqrt{3}$
Giá trị xấp xỉ: $d_{khối} \approx 1.732a$
Ví dụ: Hình lập phương cạnh 6 cm:
- $d_{khối} = 6\sqrt{3} \approx 6 \times 1.732 = 10.39$ cm
3. Công thức tìm cạnh khi biết đường chéo
a) Biết đường chéo mặt:
Từ $d_{mặt} = a\sqrt{2}$, suy ra: $$\boxed{a = \frac{d_{mặt}}{\sqrt{2}} = \frac{d_{mặt}\sqrt{2}}{2}}$$
Ví dụ: Đường chéo mặt 10 cm:
- $a = \frac{10}{\sqrt{2}} = \frac{10\sqrt{2}}{2} = 5\sqrt{2} \approx 7.07$ cm
b) Biết đường chéo khối:
Từ $d_{khối} = a\sqrt{3}$, suy ra: $$\boxed{a = \frac{d_{khối}}{\sqrt{3}} = \frac{d_{khối}\sqrt{3}}{3}}$$
Ví dụ: Đường chéo khối 12 cm:
- $a = \frac{12}{\sqrt{3}} = \frac{12\sqrt{3}}{3} = 4\sqrt{3} \approx 6.93$ cm
4. Bảng tổng hợp đường chéo theo cạnh
| Cạnh | Đường chéo mặt ($a\sqrt{2}$) | Đường chéo khối ($a\sqrt{3}$) |
|---|---|---|
| 1 cm | $\sqrt{2} \approx 1.41$ cm | $\sqrt{3} \approx 1.73$ cm |
| 2 cm | $2\sqrt{2} \approx 2.83$ cm | $2\sqrt{3} \approx 3.46$ cm |
| 3 cm | $3\sqrt{2} \approx 4.24$ cm | $3\sqrt{3} \approx 5.20$ cm |
| 4 cm | $4\sqrt{2} \approx 5.66$ cm | $4\sqrt{3} \approx 6.93$ cm |
| 5 cm | $5\sqrt{2} \approx 7.07$ cm | $5\sqrt{3} \approx 8.66$ cm |
| 6 cm | $6\sqrt{2} \approx 8.49$ cm | $6\sqrt{3} \approx 10.39$ cm |
| 7 cm | $7\sqrt{2} \approx 9.90$ cm | $7\sqrt{3} \approx 12.12$ cm |
| 8 cm | $8\sqrt{2} \approx 11.31$ cm | $8\sqrt{3} \approx 13.86$ cm |
| 9 cm | $9\sqrt{2} \approx 12.73$ cm | $9\sqrt{3} \approx 15.59$ cm |
| 10 cm | $10\sqrt{2} \approx 14.14$ cm | $10\sqrt{3} \approx 17.32$ cm |
Nhận xét: Đường chéo khối luôn dài hơn đường chéo mặt.
V. BẢNG TỔNG HỢP TẤT CẢ CÔNG THỨC
Bảng công thức đầy đủ hình lập phương
| Đại lượng | Công thức | Đơn vị | Cách nhớ |
|---|---|---|---|
| Thể tích | $V = a^3$ | m³, cm³, dm³ | “a mũ 3” |
| Diện tích 1 mặt | $S_{mặt} = a^2$ | m², cm², dm² | “a bình” |
| Diện tích xung quanh | $S_{xq} = 4a^2$ | m², cm², dm² | “4 mặt bên” |
| Diện tích toàn phần | $S_{tp} = 6a^2$ | m², cm², dm² | “6 mặt vuông” |
| Đường chéo mặt | $d_{mặt} = a\sqrt{2}$ | m, cm, dm | “Mặt căn 2” |
| Đường chéo khối | $d_{khối} = a\sqrt{3}$ | m, cm, dm | “Khối căn 3” |
| Chu vi 1 mặt | $P = 4a$ | m, cm, dm | “4 cạnh” |
| Tổng độ dài 12 cạnh | $L = 12a$ | m, cm, dm | “12 cạnh” |
Công thức tính ngược (tìm cạnh $a$)
| Biết | Công thức tìm $a$ | Ví dụ |
|---|---|---|
| Thể tích $V$ | $a = \sqrt[3]{V}$ | $V=64$ → $a=4$ |
| Diện tích 1 mặt | $a = \sqrt{S_{mặt}}$ | $S=25$ → $a=5$ |
| Diện tích xung quanh | $a = \sqrt{\frac{S_{xq}}{4}}$ | $S_{xq}=64$ → $a=4$ |
| Diện tích toàn phần | $a = \sqrt{\frac{S_{tp}}{6}}$ | $S_{tp}=150$ → $a=5$ |
| Đường chéo mặt | $a = \frac{d_{mặt}}{\sqrt{2}}$ | $d=10\sqrt{2}$ → $a=10$ |
| Đường chéo khối | $a = \frac{d_{khối}}{\sqrt{3}}$ | $d=6\sqrt{3}$ → $a=6$ |
VI. VÍ DỤ MINH HỌA CHI TIẾT
Dạng 1: Tính thể tích khi biết cạnh
Ví dụ 1: Một khối Rubik có cạnh 6 cm. Tính thể tích khối Rubik.
Lời giải:
- Cạnh: $a = 6$ cm
- Công thức: $V = a^3$
- Thể tích: $V = 6^3 = 6 \times 6 \times 6 = 216$ cm³
Đáp số: 216 cm³
Ví dụ 2: Một hộp quà hình lập phương có cạnh 15 cm. Tính thể tích hộp quà theo đơn vị cm³ và lít.
Lời giải:
- Cạnh: $a = 15$ cm
- Thể tích: $V = 15^3 = 15 \times 15 \times 15 = 3375$ cm³
- Quy đổi: $3375$ cm³ = $3.375$ dm³ = $3.375$ lít
Đáp số: 3375 cm³ (hoặc 3.375 lít)
Dạng 2: Tính cạnh khi biết thể tích
Ví dụ 3: Một bể nước hình lập phương có thể tích 8 m³. Tính độ dài cạnh bể.
Lời giải:
- Thể tích: $V = 8$ m³
- Công thức: $a = \sqrt[3]{V}$
- Cạnh: $a = \sqrt[3]{8} = 2$ m = 200 cm
Đáp số: 2 m (hoặc 200 cm)
Giải thích: $2^3 = 8$, nên $\sqrt[3]{8} = 2$
Ví dụ 4: Một khối lập phương có thể tích 343 cm³. Tính độ dài cạnh.
Lời giải:
- Thể tích: $V = 343$ cm³
- Nhận biết: $343 = 7^3$ (từ bảng lập phương)
- Cạnh: $a = 7$ cm
Đáp số: 7 cm
Dạng 3: Tính diện tích toàn phần và xung quanh
Ví dụ 5: Hình lập phương có cạnh 4 cm. Tính diện tích xung quanh và diện tích toàn phần.
Lời giải:
Diện tích xung quanh:
- $S_{xq} = 4a^2 = 4 \times 4^2 = 4 \times 16 = 64$ cm²
Diện tích toàn phần:
- $S_{tp} = 6a^2 = 6 \times 4^2 = 6 \times 16 = 96$ cm²
Đáp số: $S_{xq} = 64$ cm², $S_{tp} = 96$ cm²
Ví dụ 6: Một hộp quà hình lập phương cạnh 12 cm cần bọc giấy. Tính diện tích giấy cần dùng (bỏ qua phần dán và lãng phí).
Lời giải:
- Diện tích giấy cần dùng = Diện tích toàn phần
- $S_{tp} = 6 \times 12^2 = 6 \times 144 = 864$ cm²
Đáp số: 864 cm²
Ứng dụng: Biết giá giấy/m² có thể tính chi phí bọc quà.
Dạng 4: Tính cạnh khi biết diện tích
Ví dụ 7: Hình lập phương có diện tích toàn phần 294 cm². Tính cạnh và thể tích.
Lời giải:
Bước 1: Tính cạnh
- Từ $S_{tp} = 6a^2 = 294$
- $a^2 = \frac{294}{6} = 49$
- $a = \sqrt{49} = 7$ cm
Bước 2: Tính thể tích
- $V = a^3 = 7^3 = 343$ cm³
Đáp số: Cạnh $a = 7$ cm, Thể tích $V = 343$ cm³
Dạng 5: Tính đường chéo
Ví dụ 8: Hình lập phương có cạnh 10 cm. Tính đường chéo mặt và đường chéo khối.
Lời giải:
Đường chéo mặt:
- $d_{mặt} = a\sqrt{2} = 10\sqrt{2} \approx 10 \times 1.414 = 14.14$ cm
Đường chéo khối:
- $d_{khối} = a\sqrt{3} = 10\sqrt{3} \approx 10 \times 1.732 = 17.32$ cm
Đáp số:
- Đường chéo mặt: $10\sqrt{2} \approx 14.14$ cm
- Đường chéo khối: $10\sqrt{3} \approx 17.32$ cm
Ví dụ 9: Một khối lập phương có đường chéo khối dài $6\sqrt{3}$ cm. Tính cạnh và thể tích.
Lời giải:
Bước 1: Tính cạnh
- Từ $d_{khối} = a\sqrt{3} = 6\sqrt{3}$
- $a = 6$ cm
Bước 2: Tính thể tích
- $V = 6^3 = 216$ cm³
Đáp số: Cạnh $a = 6$ cm, Thể tích $V = 216$ cm³
Dạng 6: Bài toán thực tế
Ví dụ 10: Một thùng nước hình lập phương có cạnh 50 cm. Người ta đổ đầy nước vào thùng. Hỏi thùng chứa bao nhiêu lít nước?
Lời giải:
Bước 1: Tính thể tích thùng
- $V = 50^3 = 50 \times 50 \times 50 = 125,000$ cm³
Bước 2: Quy đổi sang lít
- $125,000$ cm³ = $125$ dm³ = $125$ lít
Đáp số: 125 lít
Giải thích: $1$ dm³ = $1$ lít, và $1000$ cm³ = $1$ dm³
VII. MỐI LIÊN HỆ GIỮA CÁC CÔNG THỨC
1. Mối quan hệ giữa thể tích và diện tích
Nếu biết cạnh $a$:
- Thể tích: $V = a^3$
- Diện tích toàn phần: $S_{tp} = 6a^2$
- Diện tích một mặt: $S_{mặt} = a^2$
Quan hệ: $$V = a \times S_{mặt}$$
Tỉ lệ: $$\frac{V}{S_{tp}} = \frac{a^3}{6a^2} = \frac{a}{6}$$
Suy ra: $$a = \frac{6V}{S_{tp}}$$
Ứng dụng: Khi biết cả thể tích và diện tích toàn phần, có thể tính cạnh bằng công thức trên.
2. Quy luật tăng kích thước
Khi tăng cạnh hình lập phương lên $k$ lần:
| Đại lượng thay đổi | Quy luật | Ví dụ ($k=2$) |
|---|---|---|
| Cạnh | Tăng $k$ lần | $a → 2a$ |
| Diện tích | Tăng $k^2$ lần | $S → 4S$ |
| Thể tích | Tăng $k^3$ lần | $V → 8V$ |
Ví dụ cụ thể:
- Hình 1: Cạnh 2 cm → $S_{tp} = 6 \times 4 = 24$ cm², $V = 8$ cm³
- Hình 2: Cạnh 4 cm (gấp đôi) → $S_{tp} = 6 \times 16 = 96$ cm² (gấp 4), $V = 64$ cm³ (gấp 8)
Kết luận:
- Diện tích tăng theo tỉ lệ bình phương
- Thể tích tăng theo tỉ lệ lập phương
3. So sánh với hình hộp chữ nhật
Hình lập phương là trường hợp đặc biệt của hình hộp chữ nhật:
| Công thức | Hình hộp chữ nhật | Hình lập phương |
|---|---|---|
| Thể tích | $V = a \times b \times c$ | $V = a^3$ (vì $a=b=c$) |
| Diện tích toàn phần | $S = 2(ab+bc+ca)$ | $S = 6a^2$ (vì $a=b=c$) |
| Đường chéo khối | $d = \sqrt{a^2+b^2+c^2}$ | $d = a\sqrt{3}$ (vì $a=b=c$) |
Chứng minh:
- Thay $b = a$ và $c = a$ vào công thức hình hộp chữ nhật:
- $V = a \times a \times a = a^3$ ✓
- $S = 2(a \cdot a + a \cdot a + a \cdot a) = 2 \times 3a^2 = 6a^2$ ✓
- $d = \sqrt{a^2 + a^2 + a^2} = \sqrt{3a^2} = a\sqrt{3}$ ✓
VIII. CÁC SAI LẦM THƯỜNG GẶP
1. Nhầm lẫn công thức thể tích và diện tích
❌ SAI:
- Thể tích: $V = 6a^2$ (nhầm với diện tích toàn phần)
- Diện tích toàn phần: $S = a^3$ (nhầm với thể tích)
✅ ĐÚNG:
- Thể tích: $V = a^3$ (mũ 3, đơn vị cm³, m³)
- Diện tích toàn phần: $S_{tp} = 6a^2$ (có số 6, mũ 2, đơn vị cm², m²)
Cách nhớ:
- Thể tích (3D) → mũ 3 → $a^3$
- Diện tích (2D) → mũ 2 → $a^2$
2. Nhầm đường chéo mặt và đường chéo khối
❌ SAI:
- Đường chéo mặt: $d = a\sqrt{3}$ (nhầm với đường chéo khối)
- Đường chéo khối: $d = a\sqrt{2}$ (nhầm với đường chéo mặt)
✅ ĐÚNG:
- Đường chéo mặt: $d_{mặt} = a\sqrt{2}$
- Đường chéo khối: $d_{khối} = a\sqrt{3}$
Mẹo nhớ: “Mặt Hai, Khối Ba”
- MẶT → $\sqrt{\mathbf{2}}$
- KHỐI → $\sqrt{\mathbf{3}}$
3. Quên lũy thừa (bình phương hoặc lập phương)
❌ SAI:
- $V = 3a$ (quên lập phương)
- $S_{tp} = 6a$ (quên bình phương)
✅ ĐÚNG:
- $V = a^3$ (có lũy thừa 3)
- $S_{tp} = 6a^2$ (có lũy thừa 2)
Cách tránh: Luôn kiểm tra đơn vị:
- Thể tích phải có đơn vị “khối”: cm³, m³
- Diện tích phải có đơn vị “vuông”: cm², m²
4. Nhầm lẫn đơn vị
❌ SAI:
- Cạnh 5 cm → Thể tích $V = 125$ cm² (đơn vị sai!)
- Cạnh 3 cm → Diện tích $S = 54$ cm³ (đơn vị sai!)
✅ ĐÚNG:
- Thể tích: Phải có đơn vị cm³, m³, dm³, lít
- Diện tích: Phải có đơn vị cm², m², dm²
Quy tắc: Kiểm tra kỹ đơn vị trong đáp án cuối cùng!
5. Tính sai căn bậc ba
❌ SAI:
- $\sqrt[3]{64} = 8$ (sai, vì $8^3 = 512$)
- $\sqrt[3]{125} = 25$ (sai)
✅ ĐÚNG:
- $\sqrt[3]{64} = 4$ (vì $4^3 = 64$)
- $\sqrt[3]{125} = 5$ (vì $5^3 = 125$)
Cách kiểm tra: Lập phương kết quả để kiểm tra ngược lại.
IX. MẸO VÀ KỸ THUẬT NHỚ CÔNG THỨC
1. Mẹo nhớ công thức thể tích và diện tích
Mẹo 1: “Số 3 cho khối, số 2 cho mặt”
- Thể tích (khối 3D): $V = a^3$ → Lũy thừa 3
- Diện tích (mặt 2D): $S = a^2$ → Lũy thừa 2
Mẹo 2: “6 mặt vuông bằng nhau”
- Hình lập phương có 6 mặt, mỗi mặt diện tích $a^2$
- Diện tích toàn phần: $S_{tp} = 6 \times a^2 = 6a^2$
Mẹo 3: “4 mặt bên”
- Diện tích xung quanh: 4 mặt bên, mỗi mặt $a^2$
- $S_{xq} = 4a^2$
2. Mẹo nhớ công thức đường chéo
“Mặt Hai, Khối Ba”
- Đường chéo MẶT: $\sqrt{\mathbf{2}}$ → $d_{mặt} = a\sqrt{2}$
- Đường chéo KHỐI: $\sqrt{\mathbf{3}}$ → $d_{khối} = a\sqrt{3}$
Giải thích:
- Đường chéo mặt nằm trên mặt phẳng 2D → liên quan đến $\sqrt{2}$
- Đường chéo khối đi qua không gian 3D → liên quan đến $\sqrt{3}$
3. Học thuộc bảng lập phương
Nên nhớ thuộc: $1^3, 2^3, 3^3, …, 10^3$
Lợi ích:
- Tính nhanh thể tích khi biết cạnh
- Tìm cạnh nhanh khi biết thể tích
- Tiết kiệm thời gian trong bài thi
Bảng quan trọng nhất:
- $2^3 = 8$
- $3^3 = 27$
- $4^3 = 64$
- $5^3 = 125$
- $10^3 = 1000$
4. Kiểm tra nhanh kết quả
Kiểm tra logic thể tích và diện tích:
- Khi $a > 1$: Thể tích $V > $ Diện tích $S_{tp}$
- Ví dụ: $a = 5$ → $V = 125$ > $S = 150$? ← SAI! Phải $V < S$
Kiểm tra đường chéo:
- $d_{khối} > d_{mặt} > a$
- Ví dụ: $a = 10$ → $d_{khối} \approx 17.32 > d_{mặt} \approx 14.14 > 10$ ✓
Kiểm tra đơn vị:
- Thể tích: cm³, m³ (đơn vị khối)
- Diện tích: cm², m² (đơn vị vuông)
X. ỨNG DỤNG THỰC TẾ
1. Trong đời sống
Khối Rubik:
- Rubik 2×2: Cạnh ≈ 5cm
- Rubik 3×3: Cạnh ≈ 5.7cm
- Tính thể tích để ước lượng trọng lượng
Xúc xắc:
- Xúc xắc chuẩn: Cạnh khoảng 1.6cm
- Thể tích: $1.6^3 \approx 4.1$ cm³
Hộp quà:
- Hộp vuông tiết kiệm vật liệu hơn hộp chữ nhật
- Tính diện tích giấy gói = Diện tích toàn phần
2. Trong xây dựng
Gạch xây hình lập phương:
- Gạch 10×10×10 cm
- Thể tích 1 viên: $1000$ cm³ = $1$ lít
- Tính số viên gạch cần dùng
Khối bê tông:
- Đúc khối mẫu 15×15×15 cm để kiểm tra độ bền
- Thể tích: $15^3 = 3375$ cm³
3. Trong công nghiệp
Container:
- Container 6×6×6 m (dạng khối lập phương)
- Thể tích: $216$ m³
- Tối ưu hóa không gian chứa hàng
Đóng gói:
- Hộp vuông dễ xếp chồng
- Tối ưu diện tích kho bãi
4. Trong khoa học
Tinh thể muối:
- Muối ăn (NaCl) kết tinh dạng hình lập phương
- Kích thước tinh thể micro: vài micromet
Pixel 3D (Voxel):
- Đồ họa 3D dùng voxel (khối lập phương nhỏ)
- Mỗi voxel lưu thông tin màu sắc
XI. KẾT LUẬN
Tổng kết công thức quan trọng nhất
Ba công thức nền tảng:
1. Thể tích: $$\boxed{V = a^3}$$
2. Diện tích toàn phần: $$\boxed{S_{tp} = 6a^2}$$
3. Đường chéo khối: $$\boxed{d = a\sqrt{3}}$$
Xem thêm các bài viết liên quan:
- Công thức tính thể tích hình hộp chữ nhật
- Công thức tính thể tích hình trụ
- Công thức tính thể tích hình cầu
- Bài tập hình lập phương có lời giải chi tiết

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
