Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ HÌNH CẦU
- 1. Hình cầu là gì?
- 2. Phân biệt mặt cầu và khối cầu
- 3. Các thành phần của hình cầu
- II. CÔNG THỨC DIỆN TÍCH MẶT CẦU
- 1. Công thức diện tích mặt cầu
- 2. Giải thích công thức
- 3. Ví dụ minh họa
- III. CÔNG THỨC THỂ TÍCH HÌNH CẦU
- 1. Công thức thể tích khối cầu
- 2. Lưu ý CỰC KỲ QUAN TRỌNG về hệ số
- 3. Ví dụ minh họa
- 4. Quan hệ giữa diện tích và thể tích
- IV. CÔNG THỨC TÍNH BÁN KÍNH MẶT CẦU
- 1. Tính bán kính khi biết diện tích mặt cầu
- 2. Tính bán kính khi biết thể tích khối cầu
- 3. Tính bán kính khi biết đường kính
- 4. Tính bán kính khi biết chu vi đường tròn lớn
- 5. Bảng tổng hợp công thức tính bán kính
- V. BẢNG TỔNG HỢP CÔNG THỨC HÌNH CẦU
- Bảng 1: Công thức chính
- Bảng 2: Công thức với đường kính
- Bảng 3: Công thức tính ngược
- Bảng 4: Quan hệ khi thay đổi bán kính
- VI. BÀI TẬP MẪU CÓ LỜI GIẢI
- VII. MẸO VÀ LƯU Ý KHI TÍNH TOÁN
- 1. Các sai lầm thường gặp
- 2. Mẹo nhớ công thức
- 3. Kiểm tra nhanh kết quả
- 4. Quy tắc vàng giải bài
- 5. Ứng dụng đặc biệt
- VIII. KẾT LUẬN
- 2 điểm CỰC KỲ QUAN TRỌNG
- Đặc điểm độc đáo của hình cầu
I. GIỚI THIỆU VỀ HÌNH CẦU
1. Hình cầu là gì?
Định nghĩa: Hình cầu (hay mặt cầu) là tập hợp tất cả các điểm trong không gian cách đều một điểm cố định (gọi là tâm) một khoảng bằng $r$ (gọi là bán kính).
Hình dung trực quan:
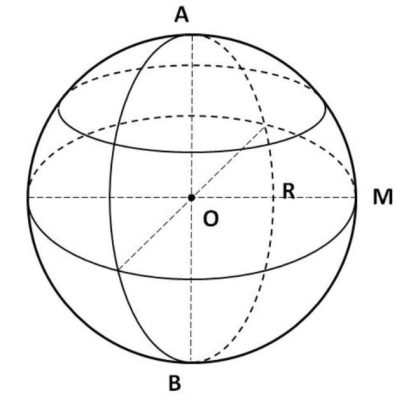
Mọi điểm trên mặt cầu đều có tính chất: khoảng cách từ điểm đó đến tâm O đều bằng r.
Cách hình thành hình cầu:
Phương pháp 1: Quay một nửa đường tròn quanh đường kính của nó
Phương pháp 2: Tập hợp tất cả các điểm trong không gian thỏa mãn điều kiện $OM = r$ (với O là tâm cố định)
Đặc điểm:
- Hình cầu là khối đối xứng hoàn hảo
- Mọi tiết diện qua tâm đều là hình tròn có bán kính $r$
- Tiết diện lớn nhất là đường tròn lớn (qua tâm)
2. Phân biệt mặt cầu và khối cầu
| Khái niệm | Mô tả chi tiết | Ví dụ thực tế |
|---|---|---|
| Mặt cầu | Bề mặt ngoài, vỏ cầu (mặt 2 chiều) | Vỏ bóng đá, vỏ bóng rổ, vỏ quả địa cầu |
| Khối cầu | Phần không gian bên trong kể cả vỏ (khối 3 chiều) | Quả bóng đặc, quả cam, viên bi |
Phân biệt khi tính toán:
- Diện tích → tính cho mặt cầu (bề mặt bao quanh)
- Thể tích → tính cho khối cầu (phần không gian chiếm chỗ)
Ví dụ minh họa:
- Sơn quả bóng → tính diện tích mặt cầu (cần biết bao nhiêu sơn)
- Bơm không khí vào bóng → tính thể tích khối cầu (cần biết bao nhiêu không khí)
3. Các thành phần của hình cầu
| Thành phần | Ký hiệu | Mô tả chi tiết |
|---|---|---|
| Tâm | $O$ | Điểm chính giữa hình cầu, cách đều mọi điểm trên mặt cầu |
| Bán kính | $r$ | Khoảng cách từ tâm O đến bất kỳ điểm nào trên mặt cầu |
| Đường kính | $d$ | Đoạn thẳng đi qua tâm, nối hai điểm đối diện trên mặt cầu |
Mối quan hệ giữa đường kính và bán kính:
$$\boxed{d = 2r} \quad \text{hoặc} \quad \boxed{r = \frac{d}{2}}$$
Lưu ý quan trọng: Trong hầu hết các công thức, chúng ta sử dụng bán kính $r$. Nếu đề bài cho đường kính $d$, cần đổi sang bán kính ngay!
II. CÔNG THỨC DIỆN TÍCH MẶT CẦU
1. Công thức diện tích mặt cầu
Đây là công thức quan trọng nhất để tính diện tích bề mặt của hình cầu:
$$\boxed{S = 4\pi r^2}$$
Hoặc nếu đề bài cho đường kính $d = 2r$:
$$\boxed{S = \pi d^2}$$
Trong đó:
- $S$: Diện tích mặt cầu (đơn vị: cm², m², dm²)
- $r$: Bán kính của hình cầu (đơn vị: cm, m, dm)
- $d$: Đường kính của hình cầu (đơn vị: cm, m, dm)
- $\pi \approx 3.14$ hoặc $\frac{22}{7}$
Cách nhớ: “4 pi r bình phương” hoặc “Bốn lần diện tích hình tròn lớn”
2. Giải thích công thức
Nguồn gốc công thức:
Diện tích mặt cầu bằng 4 lần diện tích hình tròn lớn (đường tròn lớn nhất có bán kính $r$ nằm trên mặt cầu).
Vì diện tích hình tròn bán kính $r$ là: $$S_{\text{hình tròn}} = \pi r^2$$
Do đó, diện tích mặt cầu: $$S_{\text{mặt cầu}} = 4 \times \pi r^2 = 4\pi r^2$$
Hình dung: Nếu bạn trải phẳng mặt cầu ra, nó sẽ có diện tích bằng 4 hình tròn có cùng bán kính $r$.
3. Ví dụ minh họa
Ví dụ 1: Tính diện tích mặt cầu có bán kính $r = 5$ cm.
Lời giải:
Áp dụng công thức: $$S = 4\pi r^2$$ $$= 4 \times 3.14 \times 5^2$$ $$= 4 \times 3.14 \times 25$$ $$= 314 \text{ cm}^2$$
Kết luận: Diện tích mặt cầu là 314 cm².
Ví dụ 2: Quả bóng đá có đường kính 22 cm. Tính diện tích bề mặt quả bóng.
Lời giải:
Bước 1: Đổi đường kính sang bán kính $$r = \frac{d}{2} = \frac{22}{2} = 11 \text{ cm}$$
Bước 2: Tính diện tích $$S = 4 \times 3.14 \times 11^2$$ $$= 4 \times 3.14 \times 121$$ $$= 1519.76 \text{ cm}^2$$
Cách khác: Dùng công thức với đường kính $$S = \pi d^2 = 3.14 \times 22^2 = 3.14 \times 484 = 1519.76 \text{ cm}^2$$
Kết luận: Diện tích bề mặt quả bóng đá là 1519.76 cm².
Ví dụ 3: Trái Đất có bán kính khoảng 6400 km. Tính diện tích bề mặt Trái Đất (đơn vị: triệu km²).
Lời giải:
$$S = 4 \times 3.14 \times 6400^2$$ $$= 4 \times 3.14 \times 40960000$$ $$= 513984000 \text{ km}^2$$ $$\approx 514 \text{ triệu km}^2$$
Kết luận: Diện tích bề mặt Trái Đất khoảng 514 triệu km².
Ghi chú: Giá trị thực tế của diện tích bề mặt Trái Đất là khoảng 510 triệu km² (do Trái Đất không phải hình cầu hoàn hảo).
Ví dụ 4: Nếu tăng bán kính gấp đôi thì diện tích thay đổi như thế nào?
Lời giải:
Ban đầu: Bán kính $r$, diện tích: $$S_1 = 4\pi r^2$$
Sau khi tăng: Bán kính $2r$, diện tích: $$S_2 = 4\pi(2r)^2 = 4\pi \times 4r^2 = 16\pi r^2$$
So sánh: $$\frac{S_2}{S_1} = \frac{16\pi r^2}{4\pi r^2} = 4$$
Kết luận: Khi bán kính tăng gấp đôi, diện tích tăng gấp 4 lần (bằng bình phương của 2).
Tổng quát: Nếu bán kính tăng $k$ lần thì diện tích tăng $k^2$ lần.
III. CÔNG THỨC THỂ TÍCH HÌNH CẦU
1. Công thức thể tích khối cầu
Đây là công thức tính thể tích phần không gian bên trong hình cầu:
$$\boxed{V = \frac{4}{3}\pi r^3}$$
Hoặc nếu đề bài cho đường kính $d = 2r$:
$$\boxed{V = \frac{1}{6}\pi d^3}$$
Trong đó:
- $V$: Thể tích khối cầu (đơn vị: cm³, m³, dm³, lít)
- $r$: Bán kính của hình cầu (đơn vị: cm, m, dm)
- $d$: Đường kính của hình cầu (đơn vị: cm, m, dm)
- $\pi \approx 3.14$ hoặc $\frac{22}{7}$
Cách nhớ: “Bốn phần ba pi r lập phương”
2. Lưu ý CỰC KỲ QUAN TRỌNG về hệ số
⚠️ Hệ số $\frac{4}{3}$ rất dễ nhầm lẫn!
✅ ĐÚNG: $V = \frac{4}{3}\pi r^3$ (số 4 ở trên, số 3 ở dưới)
❌ SAI: $V = \frac{3}{4}\pi r^3$ (ngược lại – sai hoàn toàn!)
Mẹo kiểm tra nhanh:
- $\frac{4}{3} \approx 1.33 > 1$ (lớn hơn 1)
- $\frac{3}{4} = 0.75 < 1$ (nhỏ hơn 1)
- Thể tích khối cầu phải lớn hơn $\pi r^3$, do đó phải dùng hệ số $\frac{4}{3}$ ✓
Cách nhớ không bao giờ quên: “Hệ số 4 trên 3, không phải 3 trên 4”
3. Ví dụ minh họa
Ví dụ 1: Tính thể tích khối cầu có bán kính $r = 6$ cm.
Lời giải:
Áp dụng công thức: $$V = \frac{4}{3}\pi r^3$$ $$= \frac{4}{3} \times 3.14 \times 6^3$$ $$= \frac{4}{3} \times 3.14 \times 216$$ $$= \frac{2712.96}{3}$$ $$= 904.32 \text{ cm}^3$$
Kết luận: Thể tích khối cầu là 904.32 cm³.
Ví dụ 2: Quả bóng rổ có đường kính 24 cm. Tính thể tích không khí bên trong quả bóng.
Lời giải:
Bước 1: Đổi đường kính sang bán kính $$r = \frac{d}{2} = \frac{24}{2} = 12 \text{ cm}$$
Bước 2: Tính thể tích $$V = \frac{4}{3} \times 3.14 \times 12^3$$ $$= \frac{4}{3} \times 3.14 \times 1728$$ $$= \frac{21703.68}{3}$$ $$= 7234.56 \text{ cm}^3$$
Cách khác: Dùng công thức với đường kính $$V = \frac{1}{6} \times 3.14 \times 24^3$$ $$= \frac{1}{6} \times 3.14 \times 13824$$ $$= 7234.56 \text{ cm}^3$$
Kết luận: Thể tích không khí bên trong là 7234.56 cm³ ≈ 7.23 lít.
Ví dụ 3: Một hòn bi sắt có đường kính 2 cm. Biết khối lượng riêng của sắt là 7.8 g/cm³. Tính khối lượng của hòn bi.
Lời giải:
Bước 1: Tính bán kính $$r = \frac{2}{2} = 1 \text{ cm}$$
Bước 2: Tính thể tích $$V = \frac{4}{3} \times 3.14 \times 1^3$$ $$= \frac{4 \times 3.14}{3}$$ $$= \frac{12.56}{3}$$ $$\approx 4.19 \text{ cm}^3$$
Bước 3: Tính khối lượng $$m = V \times D = 4.19 \times 7.8 = 32.68 \text{ g}$$
Kết luận: Khối lượng hòn bi sắt là 32.68 g ≈ 33 g.
Ví dụ 4: Nếu tăng bán kính gấp 3 thì thể tích thay đổi như thế nào?
Lời giải:
Ban đầu: Bán kính $r$, thể tích: $$V_1 = \frac{4}{3}\pi r^3$$
Sau khi tăng: Bán kính $3r$, thể tích: $$V_2 = \frac{4}{3}\pi(3r)^3 = \frac{4}{3}\pi \times 27r^3 = 27 \times \frac{4}{3}\pi r^3$$
So sánh: $$\frac{V_2}{V_1} = 27$$
Kết luận: Khi bán kính tăng gấp 3, thể tích tăng gấp 27 lần (bằng lập phương của 3).
Tổng quát: Nếu bán kính tăng $k$ lần thì thể tích tăng $k^3$ lần.
4. Quan hệ giữa diện tích và thể tích
Với cùng một hình cầu có bán kính $r$, ta có mối quan hệ đặc biệt:
$$\boxed{\frac{V}{S} = \frac{r}{3}}$$
Chứng minh: $$\frac{V}{S} = \frac{\frac{4}{3}\pi r^3}{4\pi r^2} = \frac{4\pi r^3}{3} \times \frac{1}{4\pi r^2} = \frac{r}{3}$$
Ứng dụng:
- Từ diện tích có thể tính thể tích: $V = \frac{S \times r}{3}$
- Từ thể tích và diện tích có thể tính bán kính: $r = \frac{3V}{S}$
Ví dụ: Hình cầu có diện tích $S = 100$ cm² và bán kính $r = 2.82$ cm. Tính thể tích: $$V = \frac{S \times r}{3} = \frac{100 \times 2.82}{3} \approx 94 \text{ cm}^3$$
IV. CÔNG THỨC TÍNH BÁN KÍNH MẶT CẦU
Trong nhiều bài toán, đề bài cho diện tích hoặc thể tích và yêu cầu tính bán kính. Ta cần biến đổi công thức để tính ngược lại.
1. Tính bán kính khi biết diện tích mặt cầu
Từ công thức diện tích: $S = 4\pi r^2$
Biến đổi để tìm $r$: $$4\pi r^2 = S$$ $$r^2 = \frac{S}{4\pi}$$ $$\boxed{r = \sqrt{\frac{S}{4\pi}}}$$
Hoặc viết dưới dạng: $$\boxed{r = \frac{1}{2}\sqrt{\frac{S}{\pi}}}$$
Ví dụ 1: Một mặt cầu có diện tích $S = 314$ cm². Tính bán kính.
Lời giải:
Áp dụng công thức: $$r = \sqrt{\frac{S}{4\pi}}$$ $$= \sqrt{\frac{314}{4 \times 3.14}}$$ $$= \sqrt{\frac{314}{12.56}}$$ $$= \sqrt{25}$$ $$= 5 \text{ cm}$$
Kết luận: Bán kính mặt cầu là 5 cm.
Kiểm tra: $S = 4 \times 3.14 \times 25 = 314$ cm² ✓
2. Tính bán kính khi biết thể tích khối cầu
Từ công thức thể tích: $V = \frac{4}{3}\pi r^3$
Biến đổi để tìm $r$: $$\frac{4}{3}\pi r^3 = V$$ $$r^3 = \frac{3V}{4\pi}$$ $$\boxed{r = \sqrt[3]{\frac{3V}{4\pi}}}$$
Ví dụ 2: Một khối cầu có thể tích $V = 904.32$ cm³. Tính bán kính.
Lời giải:
Áp dụng công thức: $$r = \sqrt[3]{\frac{3V}{4\pi}}$$ $$= \sqrt[3]{\frac{3 \times 904.32}{4 \times 3.14}}$$ $$= \sqrt[3]{\frac{2712.96}{12.56}}$$ $$= \sqrt[3]{216}$$ $$= 6 \text{ cm}$$
Kết luận: Bán kính khối cầu là 6 cm.
Kiểm tra: $V = \frac{4}{3} \times 3.14 \times 216 = 904.32$ cm³ ✓
3. Tính bán kính khi biết đường kính
Đây là trường hợp đơn giản nhất:
$$\boxed{r = \frac{d}{2}}$$
Ví dụ 3: Quả bóng có đường kính 20 cm. Tính bán kính.
Lời giải: $$r = \frac{d}{2} = \frac{20}{2} = 10 \text{ cm}$$
Kết luận: Bán kính là 10 cm.
4. Tính bán kính khi biết chu vi đường tròn lớn
Đường tròn lớn của mặt cầu (qua tâm) có chu vi: $$C = 2\pi r$$
Từ đó suy ra: $$\boxed{r = \frac{C}{2\pi}}$$
Ví dụ 4: Chu vi đường xích đạo của Trái Đất khoảng 40,000 km. Tính bán kính Trái Đất.
Lời giải:
Áp dụng công thức: $$r = \frac{C}{2\pi}$$ $$= \frac{40000}{2 \times 3.14}$$ $$= \frac{40000}{6.28}$$ $$\approx 6369 \text{ km}$$
Kết luận: Bán kính Trái Đất khoảng 6369 km.
So sánh: Giá trị thực tế của bán kính Trái Đất tại xích đạo là khoảng 6378 km, rất gần với kết quả tính toán.
5. Bảng tổng hợp công thức tính bán kính
| Biết | Công thức tính bán kính r | Ghi chú |
|---|---|---|
| Diện tích $S$ | $r = \sqrt{\frac{S}{4\pi}}$ | Căn bậc 2 |
| Thể tích $V$ | $r = \sqrt[3]{\frac{3V}{4\pi}}$ | Căn bậc 3 |
| Đường kính $d$ | $r = \frac{d}{2}$ | Chia đôi |
| Chu vi đường tròn lớn $C$ | $r = \frac{C}{2\pi}$ | Chia cho $2\pi$ |
V. BẢNG TỔNG HỢP CÔNG THỨC HÌNH CẦU
Bảng 1: Công thức chính
| Đại lượng | Công thức | Đơn vị | Ghi chú |
|---|---|---|---|
| Diện tích mặt cầu | $S = 4\pi r^2$ | cm², m², dm² | Số 4, mũ 2 |
| Thể tích khối cầu | $V = \frac{4}{3}\pi r^3$ | cm³, m³, dm³ | Hệ số $\frac{4}{3}$, mũ 3 |
| Bán kính | $r = \frac{d}{2}$ | cm, m, dm | Một nửa đường kính |
| Đường kính | $d = 2r$ | cm, m, dm | Gấp đôi bán kính |
Bảng 2: Công thức với đường kính
| Đại lượng | Công thức theo d | Khi nào dùng |
|---|---|---|
| Diện tích | $S = \pi d^2$ | Khi đề cho đường kính |
| Thể tích | $V = \frac{1}{6}\pi d^3$ | Khi đề cho đường kính |
Bảng 3: Công thức tính ngược
| Cần tính | Biết | Công thức |
|---|---|---|
| Bán kính $r$ | Diện tích $S$ | $r = \sqrt{\frac{S}{4\pi}}$ |
| Bán kính $r$ | Thể tích $V$ | $r = \sqrt[3]{\frac{3V}{4\pi}}$ |
| Đường kính $d$ | Bán kính $r$ | $d = 2r$ |
| Thể tích $V$ | Diện tích $S$, bán kính $r$ | $V = \frac{S \cdot r}{3}$ |
Bảng 4: Quan hệ khi thay đổi bán kính
| Thay đổi bán kính | Diện tích thay đổi | Thể tích thay đổi |
|---|---|---|
| $r$ tăng gấp 2 | $S$ tăng gấp 4 ($2^2$) | $V$ tăng gấp 8 ($2^3$) |
| $r$ tăng gấp 3 | $S$ tăng gấp 9 ($3^2$) | $V$ tăng gấp 27 ($3^3$) |
| $r$ tăng gấp $k$ | $S$ tăng gấp $k^2$ | $V$ tăng gấp $k^3$ |
| $r$ giảm một nửa | $S$ giảm còn $\frac{1}{4}$ | $V$ giảm còn $\frac{1}{8}$ |
Quy luật chung:
- Diện tích tỉ lệ với bình phương bán kính
- Thể tích tỉ lệ với lập phương bán kính
VI. BÀI TẬP MẪU CÓ LỜI GIẢI
Dạng 1: Tính diện tích và thể tích cơ bản
Bài 1: Cho hình cầu có bán kính $r = 10$ cm. Tính: a) Diện tích mặt cầu
b) Thể tích khối cầu
Lời giải:
Câu a) Tính diện tích mặt cầu:
Áp dụng công thức: $$S = 4\pi r^2$$ $$= 4 \times 3.14 \times 10^2$$ $$= 4 \times 3.14 \times 100$$ $$= 1256 \text{ cm}^2$$
Câu b) Tính thể tích khối cầu:
Áp dụng công thức: $$V = \frac{4}{3}\pi r^3$$ $$= \frac{4}{3} \times 3.14 \times 10^3$$ $$= \frac{4}{3} \times 3.14 \times 1000$$ $$= \frac{12560}{3}$$ $$= 4186.67 \text{ cm}^3$$
Kết luận:
- Diện tích mặt cầu: 1256 cm²
- Thể tích khối cầu: 4186.67 cm³
Dạng 2: Tính khi biết đường kính
Bài 2: Quả bóng tennis có đường kính 6.5 cm. a) Tính diện tích bề mặt quả bóng
b) Tính thể tích quả bóng
Lời giải:
Bước 1: Đổi đường kính sang bán kính $$r = \frac{d}{2} = \frac{6.5}{2} = 3.25 \text{ cm}$$
Câu a) Tính diện tích:
$$S = 4\pi r^2$$ $$= 4 \times 3.14 \times 3.25^2$$ $$= 4 \times 3.14 \times 10.5625$$ $$= 132.665 \text{ cm}^2$$
Câu b) Tính thể tích:
$$V = \frac{4}{3}\pi r^3$$ $$= \frac{4}{3} \times 3.14 \times 3.25^3$$ $$= \frac{4}{3} \times 3.14 \times 34.328$$ $$= 143.72 \text{ cm}^3$$
Kết luận:
- Diện tích: 132.665 cm² ≈ 132.7 cm²
- Thể tích: 143.72 cm³
Dạng 3: Tính ngược bán kính
Bài 3: a) Một mặt cầu có diện tích 1256 cm². Tính bán kính.
b) Một khối cầu có thể tích 523.33 cm³. Tính bán kính.
Lời giải:
Câu a) Tính bán kính từ diện tích:
Áp dụng công thức: $$r = \sqrt{\frac{S}{4\pi}}$$ $$= \sqrt{\frac{1256}{4 \times 3.14}}$$ $$= \sqrt{\frac{1256}{12.56}}$$ $$= \sqrt{100}$$ $$= 10 \text{ cm}$$
Câu b) Tính bán kính từ thể tích:
Áp dụng công thức: $$r = \sqrt[3]{\frac{3V}{4\pi}}$$ $$= \sqrt[3]{\frac{3 \times 523.33}{4 \times 3.14}}$$ $$= \sqrt[3]{\frac{1569.99}{12.56}}$$ $$= \sqrt[3]{125}$$ $$= 5 \text{ cm}$$
Kết luận:
- Câu a: Bán kính là 10 cm
- Câu b: Bán kính là 5 cm
Dạng 4: Bài toán thực tế – Quả bóng
Bài 4: Làm một quả bóng đá bằng da có đường kính 22 cm, độ dày da 2 mm. a) Tính diện tích da cần dùng để làm quả bóng
b) Tính thể tích không khí bên trong quả bóng (bỏ qua độ dày da)
Lời giải:
Chuyển đổi: Bán kính $r = \frac{22}{2} = 11$ cm
Câu a) Tính diện tích da:
$$S = 4\pi r^2$$ $$= 4 \times 3.14 \times 11^2$$ $$= 4 \times 3.14 \times 121$$ $$= 1519.76 \text{ cm}^2$$
Kết luận a: Diện tích da cần dùng là 1519.76 cm² ≈ 1520 cm² ≈ 0.152 m².
Câu b) Tính thể tích không khí:
$$V = \frac{4}{3}\pi r^3$$ $$= \frac{4}{3} \times 3.14 \times 11^3$$ $$= \frac{4}{3} \times 3.14 \times 1331$$ $$= \frac{16716.56}{3}$$ $$= 5572.19 \text{ cm}^3$$
Chuyển đổi: $5572.19$ cm³ $= 5.572$ lít $≈ 5.6$ lít
Kết luận b: Thể tích không khí bên trong là 5.6 lít.
Dạng 5: So sánh hai hình cầu
Bài 5: Hình cầu A có bán kính 3 cm, hình cầu B có bán kính 6 cm. So sánh: a) Diện tích mặt cầu
b) Thể tích khối cầu
Lời giải:
Hình cầu A ($r_A = 3$ cm):
- Diện tích: $S_A = 4 \times 3.14 \times 3^2 = 4 \times 3.14 \times 9 = 113.04$ cm²
- Thể tích: $V_A = \frac{4}{3} \times 3.14 \times 3^3 = \frac{4}{3} \times 3.14 \times 27 = 113.04$ cm³
Hình cầu B ($r_B = 6$ cm):
- Diện tích: $S_B = 4 \times 3.14 \times 6^2 = 4 \times 3.14 \times 36 = 452.16$ cm²
- Thể tích: $V_B = \frac{4}{3} \times 3.14 \times 6^3 = \frac{4}{3} \times 3.14 \times 216 = 904.32$ cm³
So sánh:
Câu a) Diện tích: $$\frac{S_B}{S_A} = \frac{452.16}{113.04} = 4$$
Kết luận: Diện tích B gấp 4 lần diện tích A (vì bán kính gấp 2 → diện tích gấp $2^2 = 4$)
Câu b) Thể tích: $$\frac{V_B}{V_A} = \frac{904.32}{113.04} = 8$$
Kết luận: Thể tích B gấp 8 lần thể tích A (vì bán kính gấp 2 → thể tích gấp $2^3 = 8$)
Dạng 6: Bài toán khối lượng
Bài 6: Một viên bi thủy tinh có đường kính 1.6 cm. Biết khối lượng riêng của thủy tinh là 2.5 g/cm³. Tính khối lượng của viên bi.
Lời giải:
Bước 1: Tính bán kính $$r = \frac{d}{2} = \frac{1.6}{2} = 0.8 \text{ cm}$$
Bước 2: Tính thể tích $$V = \frac{4}{3}\pi r^3$$ $$= \frac{4}{3} \times 3.14 \times 0.8^3$$ $$= \frac{4}{3} \times 3.14 \times 0.512$$ $$= \frac{6.43}{3}$$ $$= 2.144 \text{ cm}^3$$
Bước 3: Tính khối lượng $$m = V \times D = 2.144 \times 2.5 = 5.36 \text{ g}$$
Kết luận: Khối lượng viên bi thủy tinh là 5.36 g ≈ 5.4 g.
Dạng 7: Cắt hình cầu bởi mặt phẳng
Bài 7: Cắt hình cầu có bán kính 10 cm bởi mặt phẳng cách tâm 6 cm. Tính diện tích hình tròn thiết diện.
Lời giải:
Phân tích: Khi cắt hình cầu bằng mặt phẳng, thiết diện là một hình tròn.
Bước 1: Áp dụng định lý Pythagore trong tam giác vuông
- Cạnh huyền: bán kính hình cầu $R = 10$ cm
- Cạnh góc vuông: khoảng cách từ tâm đến mặt phẳng $d = 6$ cm
- Cạnh góc vuông còn lại: bán kính thiết diện $r’$
$$r’ = \sqrt{R^2 – d^2} = \sqrt{10^2 – 6^2} = \sqrt{100 – 36} = \sqrt{64} = 8 \text{ cm}$$
Bước 2: Tính diện tích thiết diện $$S = \pi r’^2 = 3.14 \times 8^2 = 3.14 \times 64 = 200.96 \text{ cm}^2$$
Kết luận: Diện tích hình tròn thiết diện là 200.96 cm².
Lưu ý:
- Thiết diện lớn nhất khi mặt phẳng đi qua tâm ($d = 0$, $r’ = R$)
- Thiết diện nhỏ dần khi mặt phẳng càng xa tâm
Dạng 8: Bài toán tối ưu
Bài 8: Một bể chứa nước hình cầu có dung tích 1000 lít. Tính bán kính của bể.
Lời giải:
Bước 1: Đổi đơn vị $$V = 1000 \text{ lít} = 1 \text{ m}^3 = 1000000 \text{ cm}^3$$
Bước 2: Áp dụng công thức tính bán kính từ thể tích $$r = \sqrt[3]{\frac{3V}{4\pi}}$$ $$= \sqrt[3]{\frac{3 \times 1000000}{4 \times 3.14}}$$ $$= \sqrt[3]{\frac{3000000}{12.56}}$$ $$= \sqrt[3]{238853.5}$$ $$\approx 62 \text{ cm}$$
Kết luận: Bán kính bể chứa nước là khoảng 62 cm = 0.62 m.
Ứng dụng thực tế: Với cùng thể tích, hình cầu có diện tích bề mặt nhỏ nhất so với mọi hình khối khác. Do đó, bể chứa hình cầu tiết kiệm vật liệu nhất!
VII. MẸO VÀ LƯU Ý KHI TÍNH TOÁN
1. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm hệ số trong công thức thể tích
Sai:
- $V = \frac{3}{4}\pi r^3$ ❌ (ngược hệ số)
- $V = \frac{4}{3}\pi r^2$ ❌ (thiếu mũ 3)
Đúng:
- $V = \frac{4}{3}\pi r^3$ ✓ (số 4 trên, số 3 dưới, mũ 3)
❌ SAI LẦM 2: Quên số 4 trong công thức diện tích
Sai:
- $S = \pi r^2$ ❌ (thiếu số 4 – đây là công thức hình tròn!)
Đúng:
- $S = 4\pi r^2$ ✓ (có số 4 phía trước)
❌ SAI LẦM 3: Nhầm lẫn giữa bán kính và đường kính
Sai:
- Đường kính 10 cm → dùng luôn 10 vào công thức với $r$ ❌
Đúng:
- Đường kính 10 cm → bán kính $r = 5$ cm ✓
- Luôn đổi đường kính sang bán kính trước khi tính!
❌ SAI LẦM 4: Nhầm mũ trong công thức
Sai:
- Diện tích: $S = 4\pi r^3$ ❌ (mũ 3 là sai)
- Thể tích: $V = \frac{4}{3}\pi r^2$ ❌ (mũ 2 là sai)
Đúng:
- Diện tích: $S = 4\pi r^2$ ✓ (mũ 2)
- Thể tích: $V = \frac{4}{3}\pi r^3$ ✓ (mũ 3)
Quy tắc nhớ:
- Diện tích (2D) → mũ 2
- Thể tích (3D) → mũ 3
2. Mẹo nhớ công thức
Công thức diện tích mặt cầu:
“4 pi r bình” = $4\pi r^2$
Cách nhớ khác: “Bốn lần diện tích hình tròn lớn”
Giải thích: Diện tích mặt cầu = 4 × (diện tích hình tròn bán kính $r$)
Công thức thể tích khối cầu:
“Bốn phần ba pi r lập phương” = $\frac{4}{3}\pi r^3$
Kiểm tra nhanh: $\frac{4}{3} \approx 1.33 > 1$ (lớn hơn 1, không phải nhỏ hơn 1)
Cách nhớ không quên: “Số 4 trên, số 3 dưới, r mũ 3”
3. Kiểm tra nhanh kết quả
Với bán kính $r = 1$ cm:
- Diện tích: $S = 4\pi \approx 4 \times 3.14 = 12.56$ cm²
- Thể tích: $V = \frac{4\pi}{3} \approx \frac{12.56}{3} = 4.19$ cm³
Ứng dụng: Nếu bạn tính được kết quả với $r = 1$, nhân với $r^2$ hoặc $r^3$ tương ứng sẽ ra đáp án!
Quy luật tỉ lệ:
Khi bán kính tăng $k$ lần:
- Diện tích tăng $k^2$ lần (bình phương)
- Thể tích tăng $k^3$ lần (lập phương)
Ví dụ:
- Bán kính tăng gấp 2 → Diện tích $\times 4$, Thể tích $\times 8$
- Bán kính tăng gấp 3 → Diện tích $\times 9$, Thể tích $\times 27$
Quan hệ giữa S và V:
$$\frac{V}{S} = \frac{r}{3}$$
Ứng dụng:
- Biết $S$ và $r$ → Tính nhanh $V = \frac{S \times r}{3}$
- Biết $V$ và $S$ → Tính nhanh $r = \frac{3V}{S}$
Ví dụ: $S = 100$ cm², $r = 3$ cm $$V = \frac{100 \times 3}{3} = 100 \text{ cm}^3$$
4. Quy tắc vàng giải bài
Bước 1: Xác định dữ liệu
- Đề cho bán kính $r$ hay đường kính $d$?
- Nếu cho $d$ → Đổi ngay $r = \frac{d}{2}$
- Ghi rõ đơn vị (cm, m, dm)
Bước 2: Chọn công thức phù hợp
- Tính diện tích → $S = 4\pi r^2$ (số 4, mũ 2)
- Tính thể tích → $V = \frac{4}{3}\pi r^3$ (hệ số $\frac{4}{3}$, mũ 3)
- Tính ngược $r$ → Dùng công thức căn bậc 2 hoặc 3
Bước 3: Đổi đơn vị về cùng hệ
- Tất cả phải cùng cm, hoặc cùng m
- Không để vừa cm vừa m!
Bước 4: Tính toán cẩn thận
- Kiểm tra hệ số: 4 hay $\frac{4}{3}$?
- Kiểm tra mũ: 2 hay 3?
- Tính lần lượt: bình phương/lập phương trước, nhân sau
Bước 5: Viết đáp số với đơn vị đúng
- Diện tích: cm², m², dm²
- Thể tích: cm³, m³, dm³, lít
5. Ứng dụng đặc biệt
Hình cầu nội tiếp hình lập phương:
Hình cầu nội tiếp hình lập phương cạnh $a$: $$r = \frac{a}{2}$$
Giải thích: Đường kính hình cầu = cạnh hình lập phương
Hình cầu ngoại tiếp hình lập phương:
Hình cầu ngoại tiếp hình lập phương cạnh $a$: $$r = \frac{a\sqrt{3}}{2}$$
Giải thích: Đường kính hình cầu = đường chéo hình lập phương = $a\sqrt{3}$
VIII. KẾT LUẬN
Bài viết đã tổng hợp đầy đủ và chi tiết các công thức hình cầu, bao gồm:
Công thức diện tích mặt cầu: $$S = 4\pi r^2$$
Đặc điểm: Có số 4, mũ 2 (diện tích 2D)
Công thức thể tích khối cầu: $$V = \frac{4}{3}\pi r^3$$
Đặc điểm: Hệ số $\frac{4}{3}$ (4 trên 3 dưới), mũ 3 (thể tích 3D)
Công thức tính bán kính:
- Từ diện tích: $r = \sqrt{\frac{S}{4\pi}}$ (căn bậc 2)
- Từ thể tích: $r = \sqrt[3]{\frac{3V}{4\pi}}$ (căn bậc 3)
- Từ đường kính: $r = \frac{d}{2}$ (chia đôi)
Quan hệ đặc biệt: $$\frac{V}{S} = \frac{r}{3}$$
2 điểm CỰC KỲ QUAN TRỌNG
1. Diện tích mặt cầu:
- Số 4 ở ngoài
- Mũ 2 (diện tích 2 chiều)
- Công thức: $4\pi r^2$
2. Thể tích khối cầu:
- Hệ số $\frac{4}{3}$ (4 trên, 3 dưới – KHÔNG NGƯỢC LẠI!)
- Mũ 3 (thể tích 3 chiều)
- Công thức: $\frac{4}{3}\pi r^3$
Kiểm tra: $\frac{4}{3} \approx 1.33 > 1$ ✓ (không phải $\frac{3}{4} = 0.75$)
Đặc điểm độc đáo của hình cầu
Tính chất hình học:
- Mọi điểm trên mặt cầu cách đều tâm một khoảng $r$
- Mọi tiết diện qua tâm đều là hình tròn có bán kính $r$
- Hình cầu có đối xứng hoàn hảo qua mọi mặt phẳng đi qua tâm
Tính chất tối ưu:
- Với cùng thể tích, hình cầu có diện tích bề mặt nhỏ nhất
- Đây là lý do tại sao:
- Giọt nước có dạng cầu (giảm năng lượng bề mặt)
- Bể chứa hình cầu tiết kiệm vật liệu nhất
- Hành tinh có dạng cầu do lực hấp dẫn
So sánh với hình trụ (cùng chiều cao $h = 2r$, bán kính $r$):
- Thể tích: $V_{\text{cầu}} = \frac{2}{3}V_{\text{trụ}}$
- Diện tích xung quanh: $S_{\text{cầu}} = S_{\text{xq trụ}}$
Xem thêm các chủ đề liên quan:
- [Công thức hình trụ – Bảng tổng hợp đầy đủ]
- [Công thức hình nón – Chi tiết và ứng dụng]
- [Công thức hình nón cụt – Đầy đủ nhất]
- [So sánh các khối tròn xoay: Trụ, Nón, Cầu]
- [Bài tập hình học không gian – Có lời giải chi tiết]

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
