Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ CHỎM CẦU
- 1. Định nghĩa chỏm cầu
- 2. Công thức liên hệ giữa R, h, r
- II. CÔNG THỨC DIỆN TÍCH CHỎM CẦU
- 1. Diện tích mặt chỏm cầu (diện tích xung quanh)
- 2. Diện tích đáy chỏm cầu
- 3. Diện tích toàn phần chỏm cầu
- III. CÔNG THỨC THỂ TÍCH CHỎM CẦU
- 1. Công thức thể tích chỏm cầu (công thức chính)
- 2. Công thức khi biết r và h
- 3. Trường hợp đặc biệt: Nửa hình cầu
- 4. So sánh với thể tích khối cầu
- IV. CÁC DẠNG BÀI TẬP TRỌNG TÂM
- Dạng 1: Tính diện tích và thể tích khi biết R và h
- Dạng 2: Tính các yếu tố khi biết 2 trong 3 đại lượng R, h, r
- Dạng 3: Bài toán thực tế – Thể tích nước trong bể
- Dạng 4: Tính tỷ số thể tích
- Dạng 5: Mái vòm hình chỏm cầu
- Dạng 6: Chỏm cầu lồng trong hình trụ
- V. BẢNG CÔNG THỨC TỔNG HỢP
- Bảng công thức chính
- Các công thức liên quan
- VI. MẸO VÀ LƯU Ý QUAN TRỌNG
- 1. Các sai lầm thường gặp
- 2. Mẹo nhớ công thức
- 3. Cách nhận dạng bài toán
- 4. Thứ tự giải bài chuẩn
- VII. KẾT LUẬN
- Tổng kết
I. GIỚI THIỆU VỀ CHỎM CẦU
1. Định nghĩa chỏm cầu
Chỏm cầu (mặt chỏm cầu): Là phần mặt cầu bị cắt bởi một mặt phẳng.
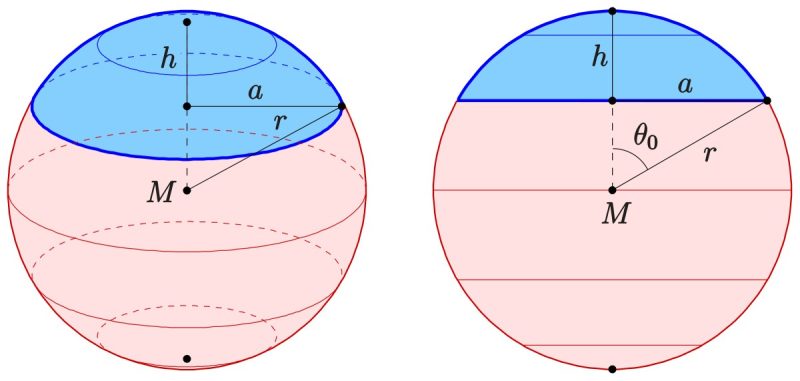
Khối chỏm cầu: Là phần khối cầu giới hạn bởi chỏm cầu (mặt cong) và mặt phẳng cắt (đáy phẳng).
Hình dung đơn giản: Chỏm cầu giống như “nắp” của một quả bóng khi bạn cắt ngang quả bóng đó.
Các thành phần:
| Yếu tố | Ký hiệu | Mô tả |
|---|---|---|
| Bán kính mặt cầu | $R$ | Bán kính của hình cầu ban đầu |
| Chiều cao chỏm cầu | $h$ | Khoảng cách từ đỉnh chỏm cầu đến mặt phẳng cắt |
| Bán kính đáy | $r$ | Bán kính của hình tròn giao tuyến (đáy chỏm cầu) |
Lưu ý quan trọng:
- $0 < h \leq 2R$ (chiều cao không vượt quá đường kính)
- Khi $h = R$: chỏm cầu là nửa hình cầu
- Khi $h = 2R$: chỏm cầu là toàn bộ hình cầu
2. Công thức liên hệ giữa R, h, r
Đây là công thức cực kỳ quan trọng, xuất hiện trong hầu hết các bài toán:
$$\boxed{r^2 = R^2 – (R – h)^2 = 2Rh – h^2}$$
Hoặc viết dưới dạng: $$\boxed{r^2 = h(2R – h)}$$
Chứng minh: Áp dụng định lý Pythagore trong tam giác vuông tạo bởi:
- Bán kính mặt cầu $R$ (cạnh huyền)
- Khoảng cách từ tâm đến mặt phẳng cắt: $(R – h)$
- Bán kính đáy $r$
Ta có: $r^2 + (R-h)^2 = R^2$
Suy ra: $r^2 = R^2 – (R-h)^2 = R^2 – R^2 + 2Rh – h^2 = 2Rh – h^2$
Ứng dụng: Công thức này giúp tính $r$ khi biết $R$ và $h$, hoặc ngược lại.
II. CÔNG THỨC DIỆN TÍCH CHỎM CẦU
1. Diện tích mặt chỏm cầu (diện tích xung quanh)
Công thức:
$$\boxed{S_{xq} = 2\pi Rh}$$
Trong đó:
- $S_{xq}$: Diện tích mặt cong của chỏm cầu (cm², m², dm²)
- $R$: Bán kính mặt cầu (cm, m, dm)
- $h$: Chiều cao chỏm cầu (cm, m, dm)
Đặc điểm quan trọng: Diện tích chỉ phụ thuộc vào $R$ và $h$, không phụ thuộc vào $r$ (bán kính đáy).
Cách nhớ: “2 pi R h” – giống công thức diện tích xung quanh hình trụ
Ví dụ 1: Tính diện tích mặt chỏm cầu có bán kính $R = 10$ cm, chiều cao $h = 6$ cm.
Lời giải:
Áp dụng công thức: $$S_{xq} = 2\pi Rh$$ $$= 2 \times 3.14 \times 10 \times 6$$ $$= 376.8 \text{ cm}^2$$
Hoặc để nguyên dạng: $S_{xq} = 120\pi$ cm²
Kết luận: Diện tích mặt chỏm cầu là 120π cm² ≈ 376.8 cm².
2. Diện tích đáy chỏm cầu
Đáy của chỏm cầu là một hình tròn có bán kính $r$.
Công thức:
$$\boxed{S_{\text{đáy}} = \pi r^2}$$
Với: $r = \sqrt{h(2R – h)}$ (từ công thức liên hệ)
Lưu ý: Nếu đề bài không cho $r$, cần tính $r$ từ $R$ và $h$ trước!
3. Diện tích toàn phần chỏm cầu
Diện tích toàn phần bao gồm cả mặt cong và đáy:
Công thức:
$$\boxed{S_{tp} = S_{xq} + S_{\text{đáy}} = 2\pi Rh + \pi r^2}$$
Hoặc rút gọn (thay $r^2 = h(2R – h)$):
$$S_{tp} = 2\pi Rh + \pi h(2R – h)$$ $$= \pi(2Rh + 2Rh – h^2)$$ $$= \pi(4Rh – h^2)$$ $$\boxed{S_{tp} = \pi h(4R – h)}$$
Hoặc viết dạng khác: $$\boxed{S_{tp} = \pi h(2R + h)}$$ (Khi khai triển từ $2Rh + h(2R-h) = 2Rh + 2Rh – h^2$… nhưng dạng trên hay dùng hơn)
Ví dụ 2: Tính diện tích toàn phần của chỏm cầu có $R = 13$ cm, $h = 5$ cm.
Lời giải:
Bước 1: Tính bán kính đáy $$r^2 = h(2R – h) = 5(2 \times 13 – 5) = 5 \times 21 = 105$$
Bước 2: Tính diện tích xung quanh $$S_{xq} = 2\pi Rh = 2\pi \times 13 \times 5 = 130\pi \text{ cm}^2$$
Bước 3: Tính diện tích đáy $$S_{\text{đáy}} = \pi r^2 = 105\pi \text{ cm}^2$$
Bước 4: Tính diện tích toàn phần $$S_{tp} = S_{xq} + S_{\text{đáy}} = 130\pi + 105\pi = 235\pi \text{ cm}^2$$
Kết luận: Diện tích toàn phần là 235π cm² ≈ 738.2 cm².
III. CÔNG THỨC THỂ TÍCH CHỎM CẦU
1. Công thức thể tích chỏm cầu (công thức chính)
Đây là công thức quan trọng nhất của chỏm cầu:
$$\boxed{V = \pi h^2\left(R – \frac{h}{3}\right)}$$
Hoặc viết gọn hơn:
$$\boxed{V = \frac{\pi h^2(3R – h)}{3}}$$
Trong đó:
- $V$: Thể tích khối chỏm cầu (cm³, m³, dm³)
- $h$: Chiều cao chỏm cầu
- $R$: Bán kính mặt cầu
Cách nhớ: “Pi h bình, trong ngoặc 3R trừ h, chia 3”
Ví dụ 3: Tính thể tích chỏm cầu có $R = 10$ cm, $h = 6$ cm.
Lời giải:
Áp dụng công thức: $$V = \frac{\pi h^2(3R – h)}{3}$$ $$= \frac{\pi \times 6^2 \times (3 \times 10 – 6)}{3}$$ $$= \frac{\pi \times 36 \times 24}{3}$$ $$= \frac{864\pi}{3}$$ $$= 288\pi \text{ cm}^3$$
Tính số: $288 \times 3.14 \approx 904.32$ cm³
Kết luận: Thể tích chỏm cầu là 288π cm³ ≈ 904.32 cm³.
2. Công thức khi biết r và h
Khi đề bài cho bán kính đáy $r$ và chiều cao $h$ (không cho $R$):
$$\boxed{V = \frac{\pi h}{6}(3r^2 + h^2)}$$
Nguồn gốc: Từ công thức chính, thay $R = \frac{r^2 + h^2}{2h}$ (suy ra từ $r^2 = h(2R-h)$)
Ví dụ 4: Chỏm cầu có chiều cao $h = 4$ cm, bán kính đáy $r = 6$ cm. Tính thể tích.
Lời giải:
Áp dụng công thức với $r$ và $h$: $$V = \frac{\pi h}{6}(3r^2 + h^2)$$ $$= \frac{\pi \times 4}{6}(3 \times 36 + 16)$$ $$= \frac{4\pi}{6}(108 + 16)$$ $$= \frac{4\pi}{6} \times 124$$ $$= \frac{496\pi}{6}$$ $$= \frac{248\pi}{3} \text{ cm}^3$$
Kết luận: Thể tích là $\frac{248\pi}{3}$ cm³ ≈ 259.6 cm³.
3. Trường hợp đặc biệt: Nửa hình cầu
Khi $h = R$ (chiều cao bằng bán kính), chỏm cầu trở thành nửa hình cầu.
Thể tích nửa hình cầu:
Thay $h = R$ vào công thức: $$V = \frac{\pi R^2(3R – R)}{3} = \frac{\pi R^2 \times 2R}{3}$$ $$\boxed{V = \frac{2\pi R^3}{3}}$$
Diện tích xung quanh nửa hình cầu: $$S_{xq} = 2\pi R \times R$$ $$\boxed{S_{xq} = 2\pi R^2}$$
Lưu ý:
- Thể tích nửa khối cầu = $\frac{1}{2} \times$ Thể tích khối cầu
- Diện tích mặt nửa cầu = $\frac{1}{2} \times$ Diện tích mặt cầu
4. So sánh với thể tích khối cầu
| Hình | Thể tích | Quan hệ |
|---|---|---|
| Khối cầu | $V = \frac{4}{3}\pi R^3$ | Toàn bộ |
| Nửa khối cầu | $V = \frac{2}{3}\pi R^3$ | Bằng $\frac{1}{2}$ khối cầu |
| Chỏm cầu | $V = \frac{\pi h^2(3R – h)}{3}$ | Phụ thuộc $h$ |
Kiểm tra:
- Khi $h = 2R$ (toàn bộ): $V = \frac{\pi (2R)^2(6R – 2R)}{3} = \frac{4\pi R^2 \times 4R}{3} = \frac{16\pi R^3}{3}$… (Có vấn đề ở đây, công thức chỏm cầu chỉ áp dụng khi $h \leq R$)
- Khi $h = R$ (nửa cầu): $V = \frac{2\pi R^3}{3}$ ✓
IV. CÁC DẠNG BÀI TẬP TRỌNG TÂM
Dạng 1: Tính diện tích và thể tích khi biết R và h
Phương pháp: Áp dụng trực tiếp công thức.
Ví dụ 5: Cho chỏm cầu có $R = 15$ cm, $h = 9$ cm. Tính: a) Diện tích xung quanh
b) Thể tích chỏm cầu
Lời giải:
Câu a) Diện tích xung quanh: $$S_{xq} = 2\pi Rh$$ $$= 2 \times 3.14 \times 15 \times 9$$ $$= 270\pi \text{ cm}^2$$ $$\approx 847.8 \text{ cm}^2$$
Câu b) Thể tích: $$V = \frac{\pi h^2(3R – h)}{3}$$ $$= \frac{\pi \times 81 \times (45 – 9)}{3}$$ $$= \frac{\pi \times 81 \times 36}{3}$$ $$= \frac{2916\pi}{3}$$ $$= 972\pi \text{ cm}^3$$ $$\approx 3053.6 \text{ cm}^3$$
Kết luận:
- Diện tích xung quanh: 270π cm² ≈ 847.8 cm²
- Thể tích: 972π cm³ ≈ 3053.6 cm³
Dạng 2: Tính các yếu tố khi biết 2 trong 3 đại lượng R, h, r
Phương pháp: Sử dụng công thức liên hệ $r^2 = h(2R – h)$ để tìm đại lượng còn thiếu.
Ví dụ 6: Chỏm cầu có chiều cao $h = 8$ cm, bán kính đáy $r = 12$ cm. Tính bán kính $R$ và thể tích.
Lời giải:
Bước 1: Tính bán kính $R$
Từ công thức liên hệ: $$r^2 = h(2R – h)$$ $$144 = 8(2R – 8)$$ $$144 = 16R – 64$$ $$16R = 208$$ $$R = 13 \text{ cm}$$
Bước 2: Tính thể tích
Cách 1: Dùng công thức với $R$ và $h$ $$V = \frac{\pi h^2(3R – h)}{3}$$ $$= \frac{\pi \times 64 \times (39 – 8)}{3}$$ $$= \frac{\pi \times 64 \times 31}{3}$$ $$= \frac{1984\pi}{3} \text{ cm}^3$$
Cách 2: Dùng công thức với $r$ và $h$ $$V = \frac{\pi h}{6}(3r^2 + h^2)$$ $$= \frac{\pi \times 8}{6}(3 \times 144 + 64)$$ $$= \frac{8\pi}{6}(432 + 64)$$ $$= \frac{8\pi \times 496}{6}$$ $$= \frac{3968\pi}{6} = \frac{1984\pi}{3} \text{ cm}^3$$
Kết luận:
- Bán kính mặt cầu: $R = 13$ cm
- Thể tích: $\frac{1984\pi}{3}$ cm³ ≈ 2075.4 cm³
Dạng 3: Bài toán thực tế – Thể tích nước trong bể
Ví dụ 7: Một bể nước hình cầu có bán kính $R = 2$ m chứa nước đến độ cao $h = 1.5$ m (tính từ đáy bể). Tính thể tích nước trong bể.
Lời giải:
Đây là bài toán tính thể tích chỏm cầu với:
- Bán kính mặt cầu: $R = 2$ m
- Chiều cao mực nước: $h = 1.5$ m
Áp dụng công thức: $$V = \frac{\pi h^2(3R – h)}{3}$$ $$= \frac{\pi \times 1.5^2 \times (3 \times 2 – 1.5)}{3}$$ $$= \frac{\pi \times 2.25 \times 4.5}{3}$$ $$= \frac{10.125\pi}{3}$$ $$= 3.375\pi \text{ m}^3$$
Tính số: $3.375 \times 3.14 \approx 10.6$ m³
Chuyển đổi: 10.6 m³ = 10,600 lít
Kết luận: Thể tích nước trong bể là 3.375π m³ ≈ 10.6 m³ = 10,600 lít.
Dạng 4: Tính tỷ số thể tích
Ví dụ 8: Một mặt phẳng chia hình cầu bán kính $R$ thành hai chỏm cầu có chiều cao $h_1$ và $h_2 = 2R – h_1$. Tính tỷ số thể tích hai chỏm cầu khi $h_1 = \frac{R}{2}$.
Lời giải:
Bước 1: Xác định chiều cao hai chỏm cầu
- Chỏm cầu 1: $h_1 = \frac{R}{2}$
- Chỏm cầu 2: $h_2 = 2R – \frac{R}{2} = \frac{3R}{2}$
Bước 2: Tính thể tích chỏm cầu 1 $$V_1 = \frac{\pi h_1^2(3R – h_1)}{3}$$ $$= \frac{\pi \times \left(\frac{R}{2}\right)^2 \times \left(3R – \frac{R}{2}\right)}{3}$$ $$= \frac{\pi \times \frac{R^2}{4} \times \frac{5R}{2}}{3}$$ $$= \frac{\pi \times \frac{5R^3}{8}}{3}$$ $$= \frac{5\pi R^3}{24}$$
Bước 3: Tính thể tích chỏm cầu 2 $$V_2 = \frac{\pi h_2^2(3R – h_2)}{3}$$ $$= \frac{\pi \times \left(\frac{3R}{2}\right)^2 \times \left(3R – \frac{3R}{2}\right)}{3}$$ $$= \frac{\pi \times \frac{9R^2}{4} \times \frac{3R}{2}}{3}$$ $$= \frac{\pi \times \frac{27R^3}{8}}{3}$$ $$= \frac{27\pi R^3}{24} = \frac{9\pi R^3}{8}$$
Bước 4: Tính tỷ số $$\frac{V_1}{V_2} = \frac{\frac{5\pi R^3}{24}}{\frac{9\pi R^3}{8}}$$ $$= \frac{5\pi R^3}{24} \times \frac{8}{9\pi R^3}$$ $$= \frac{5 \times 8}{24 \times 9}$$ $$= \frac{40}{216} = \frac{5}{27}$$
Kết luận: Tỷ số thể tích hai chỏm cầu là $\frac{V_1}{V_2} = \frac{5}{27}$.
Dạng 5: Mái vòm hình chỏm cầu
Ví dụ 9: Một mái vòm hình chỏm cầu có đường kính đáy 16 m, chiều cao 4 m. Tính diện tích mái vòm cần sơn.
Lời giải:
Bước 1: Xác định dữ liệu
- Đường kính đáy = 16 m → Bán kính đáy: $r = 8$ m
- Chiều cao: $h = 4$ m
Bước 2: Tính bán kính mặt cầu $R$
Từ công thức liên hệ: $$r^2 = h(2R – h)$$ $$64 = 4(2R – 4)$$ $$64 = 8R – 16$$ $$8R = 80$$ $$R = 10 \text{ m}$$
Bước 3: Tính diện tích mái vòm $$S_{xq} = 2\pi Rh$$ $$= 2 \times 3.14 \times 10 \times 4$$ $$= 80\pi \text{ m}^2$$ $$\approx 251.2 \text{ m}^2$$
Kết luận: Diện tích mái vòm cần sơn là 80π m² ≈ 251.2 m².
Dạng 6: Chỏm cầu lồng trong hình trụ
Ví dụ 10: Một chỏm cầu có chiều cao $h$ được đặt vừa khít trong hình trụ có bán kính đáy $r$ và chiều cao $h$. Biết $h = 6$ cm, $r = 4$ cm. Tính tỷ số thể tích chỏm cầu và hình trụ.
Lời giải:
Bước 1: Tính bán kính $R$ của chỏm cầu
Vì chỏm cầu vừa khít trong hình trụ nên bán kính đáy chỏm cầu bằng bán kính trụ: $r = 4$ cm
Từ công thức liên hệ: $$r^2 = h(2R – h)$$ $$16 = 6(2R – 6)$$ $$16 = 12R – 36$$ $$12R = 52$$ $$R = \frac{13}{3} \text{ cm}$$
Bước 2: Tính thể tích chỏm cầu $$V_{\text{chỏm}} = \frac{\pi h}{6}(3r^2 + h^2)$$ $$= \frac{\pi \times 6}{6}(3 \times 16 + 36)$$ $$= \pi(48 + 36)$$ $$= 84\pi \text{ cm}^3$$
Bước 3: Tính thể tích hình trụ $$V_{\text{trụ}} = \pi r^2 h$$ $$= \pi \times 16 \times 6$$ $$= 96\pi \text{ cm}^3$$
Bước 4: Tính tỷ số $$\frac{V_{\text{chỏm}}}{V_{\text{trụ}}} = \frac{84\pi}{96\pi} = \frac{84}{96} = \frac{7}{8}$$
Kết luận: Tỷ số thể tích chỏm cầu và hình trụ là $\frac{7}{8}$.
V. BẢNG CÔNG THỨC TỔNG HỢP
Bảng công thức chính
| Công thức | Biểu thức | Ghi chú |
|---|---|---|
| Liên hệ $r, R, h$ | $r^2 = h(2R – h)$ | Quan trọng nhất |
| Diện tích xung quanh | $S_{xq} = 2\pi Rh$ | Chỉ phụ thuộc $R$, $h$ |
| Diện tích đáy | $S_{\text{đáy}} = \pi r^2$ | Hình tròn |
| Diện tích toàn phần | $S_{tp} = 2\pi Rh + \pi r^2$ | Xung quanh + đáy |
| Thể tích (dạng 1) | $V = \frac{\pi h^2(3R – h)}{3}$ | Khi biết $R$, $h$ |
| Thể tích (dạng 2) | $V = \frac{\pi h}{6}(3r^2 + h^2)$ | Khi biết $r$, $h$ |
| Nửa hình cầu ($h = R$) | $V = \frac{2\pi R^3}{3}$ | Trường hợp đặc biệt |
Các công thức liên quan
| Hình | Thể tích | Diện tích xung quanh |
|---|---|---|
| Khối cầu | $V = \frac{4}{3}\pi R^3$ | $S = 4\pi R^2$ |
| Hình trụ | $V = \pi r^2h$ | $S_{xq} = 2\pi rh$ |
| Hình nón | $V = \frac{1}{3}\pi r^2h$ | $S_{xq} = \pi rl$ |
VI. MẸO VÀ LƯU Ý QUAN TRỌNG
1. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm công thức thể tích với hình nón
Sai:
- $V = \frac{1}{3}\pi r^2h$ (đây là công thức hình nón!) ❌
Đúng:
- $V = \frac{\pi h^2(3R – h)}{3}$ (công thức chỏm cầu) ✓
❌ SAI LẦM 2: Quên công thức liên hệ $r^2 = h(2R – h)$
Sai:
- Tính thể tích khi chỉ biết $r$ và $h$ mà không tìm $R$ trước ❌
Đúng:
- Dùng công thức liên hệ để tìm $R$ hoặc dùng công thức dạng 2 ✓
❌ SAI LẦM 3: Nhầm lẫn giữa $R$ và $r$
Sai:
- $R$ (bán kính mặt cầu) = $r$ (bán kính đáy) ❌
Đúng:
- $R$ luôn lớn hơn hoặc bằng $r$ ✓
- Phân biệt rõ: $R$ là bán kính cầu, $r$ là bán kính đáy
❌ SAI LẦM 4: Quên chia 3 trong công thức thể tích
Sai:
- $V = \pi h^2(3R – h)$ (thiếu chia 3) ❌
Đúng:
- $V = \frac{\pi h^2(3R – h)}{3}$ ✓
2. Mẹo nhớ công thức
Diện tích xung quanh:
“2 pi R h”
Giống hình trụ nhưng không có $r$
Thể tích:
“Pi h bình, trong ngoặc 3R trừ h, chia 3”
$$V = \frac{\pi h^2(3R – h)}{3}$$
Công thức liên hệ:
“r bình = h nhân (2R trừ h)”
$$r^2 = h(2R – h)$$
3. Cách nhận dạng bài toán
Từ khóa trong đề bài:
- “Chỏm cầu”
- “Mái vòm”
- “Nước trong bể hình cầu”
- “Phần cầu bị cắt”
- “Nửa hình cầu”
Dữ kiện thường cho:
- Thường cho 2 trong 3 đại lượng: $R$, $h$, $r$
- Cần tìm đại lượng còn thiếu bằng công thức liên hệ
Yêu cầu bài toán:
- Tính diện tích (xung quanh hoặc toàn phần)
- Tính thể tích
- Tính tỷ số
- Ứng dụng thực tế
4. Thứ tự giải bài chuẩn
Bước 1: Vẽ hình và đánh dấu
- Vẽ chỏm cầu
- Đánh dấu rõ $R$, $h$, $r$
- Xác định đề cho gì, cần tìm gì
Bước 2: Kiểm tra dữ kiện
- Đã có đủ $R$ và $h$ chưa?
- Nếu chưa → dùng công thức liên hệ để tìm
Bước 3: Chọn công thức phù hợp
- Tính diện tích → $S_{xq} = 2\pi Rh$
- Tính thể tích → $V = \frac{\pi h^2(3R-h)}{3}$
Bước 4: Tính toán
- Thay số cẩn thận
- Chú ý đơn vị
Bước 5: Viết kết luận
- Ghi rõ đơn vị (cm², cm³, m², m³…)
VII. KẾT LUẬN
Tổng kết
Bài viết đã hệ thống hóa đầy đủ kiến thức về chỏm cầu:
Định nghĩa và yếu tố: $R$ (bán kính cầu), $h$ (chiều cao), $r$ (bán kính đáy)
Công thức liên hệ quan trọng nhất: $$r^2 = h(2R – h)$$
4 công thức chính:
- Diện tích xung quanh: $S_{xq} = 2\pi Rh$
- Diện tích toàn phần: $S_{tp} = 2\pi Rh + \pi r^2$
- Thể tích (dạng 1): $V = \frac{\pi h^2(3R – h)}{3}$
- Thể tích (dạng 2): $V = \frac{\pi h}{6}(3r^2 + h^2)$
6 dạng bài tập trọng tâm:
- Tính diện tích và thể tích khi biết $R$, $h$
- Tính các yếu tố khi biết 2/3 đại lượng
- Bài toán thực tế về nước trong bể
- Tính tỷ số thể tích
- Mái vòm kiến trúc
- Chỏm cầu lồng trong hình trụ
Mẹo và lưu ý: Tránh 4 sai lầm thường gặp, mẹo nhớ công thức
Xem thêm các chủ đề liên quan:
- [Công thức hình cầu – Diện tích và thể tích đầy đủ]
- [Công thức hình nón – Chi tiết nhất]
- [Công thức hình trụ – Bảng tổng hợp]

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
