Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ HÌNH ELIP
- 1. Định nghĩa hình elip
- 2. Các yếu tố cơ bản của elip
- 3. Tính chất đặc trưng
- 4. Cấu trúc bài viết
- II. PHƯƠNG TRÌNH CHÍNH TẮC CỦA ELIP ⭐
- 1. Phương trình chính tắc (Quan trọng nhất)
- 2. Hệ thức cơ bản giữa a, b, c
- 3. Cách xác định phương trình elip
- 4. Trường hợp đặc biệt: Trục lớn theo Oy
- III. CÔNG THỨC DIỆN TÍCH ELIP ⭐
- 1. Công thức tính diện tích
- 2. Ví dụ minh họa
- 3. Ứng dụng thực tế
- IV. CÔNG THỨC CHU VI ELIP
- 1. Công thức gần đúng
- 2. Ví dụ so sánh các công thức
- 3. Lưu ý quan trọng
- V. TÂM SAI CỦA ELIP
- 1. Định nghĩa tâm sai
- 2. Ý nghĩa của tâm sai
- 3. Công thức liên quan đến tâm sai
- 4. Ví dụ minh họa
- 5. Tâm sai quỹ đạo hành tinh
- VI. CÁC CÔNG THỨC KHÁC VỀ ELIP
- 1. Phương trình tiếp tuyến
- 2. Khoảng cách tiêu điểm
- 3. Độ dài dây cung tiêu
- 4. Bán kính cong
- VII. BẢNG TỔNG HỢP CÔNG THỨC ⭐
- Bảng 1: Công thức cơ bản (Quan trọng nhất)
- Bảng 2: Mối quan hệ giữa các đại lượng
- Bảng 3: Trường hợp đặc biệt
- Bảng 4: Công thức bổ sung
- VIII. BÀI TẬP MẪU
- Dạng 1: Lập phương trình elip
- Dạng 2: Tính diện tích elip
- Dạng 3: Tính tâm sai
- Dạng 4: Tìm điểm trên elip
- Dạng 5: Bài toán tổng hợp
- IX. KẾT LUẬN
- Quy tắc vàng khi làm bài tập
I. GIỚI THIỆU VỀ HÌNH ELIP
1. Định nghĩa hình elip
Elip là một trong những đường conic quan trọng nhất trong hình học giải tích. Có hai cách định nghĩa tương đương:
Định nghĩa 1 (Hình học – Định nghĩa tiêu điểm):
Elip là tập hợp các điểm $M$ trong mặt phẳng sao cho tổng khoảng cách từ $M$ đến hai điểm cố định $F_1$, $F_2$ (gọi là tiêu điểm) là một hằng số:
$$\boxed{MF_1 + MF_2 = 2a \quad (a > 0)}$$
Trong đó:
- $F_1$, $F_2$: hai tiêu điểm
- $2a$: hằng số lớn hơn khoảng cách $F_1F_2$
Định nghĩa 2 (Giải tích – Phương trình):
Elip là đường cong có phương trình chính tắc trong hệ tọa độ Oxy:
$$\boxed{\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad (a > b > 0)}$$
Đây là định nghĩa thường dùng nhất trong giải toán.
2. Các yếu tố cơ bản của elip
Để hiểu rõ elip, ta cần nắm các yếu tố cấu tạo:
Tâm elip: Điểm $O(0; 0)$ – gốc tọa độ, là trung điểm của đoạn nối hai tiêu điểm.
Tiêu điểm: Hai điểm đặc biệt:
- $F_1(-c; 0)$ và $F_2(c; 0)$
- Trong đó: $c^2 = a^2 – b^2$
Các trục:
- Trục lớn (trục chính): Độ dài $2a$, nằm dọc theo trục $Ox$
- Trục nhỏ (trục phụ): Độ dài $2b$, nằm dọc theo trục $Oy$
Bán trục:
- Bán trục lớn: $a$ (một nửa trục lớn)
- Bán trục nhỏ: $b$ (một nửa trục nhỏ)
Các đỉnh:
- Đỉnh trên trục lớn: $A_1(-a; 0)$ và $A_2(a; 0)$
- Đỉnh trên trục nhỏ: $B_1(0; -b)$ và $B_2(0; b)$
Tiêu cự: Khoảng cách giữa hai tiêu điểm: $F_1F_2 = 2c$
3. Tính chất đặc trưng
Tính đối xứng:
- Elip đối xứng qua trục $Ox$ (trục hoành)
- Elip đối xứng qua trục $Oy$ (trục tung)
- Elip đối xứng qua gốc tọa độ $O$
Tính chất đường cong:
- Elip là đường cong kín (không có điểm ở vô cùng)
- Elip là đường cong trơn (không có góc nhọn)
- Mọi điểm trên elip đều thỏa mãn: $MF_1 + MF_2 = 2a$
Quan hệ với đường tròn:
- Elip là trường hợp tổng quát của đường tròn
- Khi $a = b$, elip trở thành đường tròn bán kính $r = a$
- Đường tròn là elip có tâm sai $e = 0$
Tiêu cự:
- $F_1F_2 = 2c$ với $c = \sqrt{a^2 – b^2}$
- $c < a$ (tiêu cự nhỏ hơn trục lớn)
4. Cấu trúc bài viết
Bài viết sẽ trình bày theo trình tự:
- Phần II: Phương trình chính tắc (nền tảng quan trọng nhất)
- Phần III: Công thức diện tích (công thức hay dùng nhất)
- Phần IV: Công thức chu vi elip
- Phần V: Tâm sai và ý nghĩa
- Phần VI: Các công thức khác (tiếp tuyến, khoảng cách tiêu điểm)
- Phần VII: Bảng tổng hợp công thức
- Phần VIII: Bài tập mẫu từng dạng
II. PHƯƠNG TRÌNH CHÍNH TẮC CỦA ELIP ⭐
1. Phương trình chính tắc (Quan trọng nhất)
Đây là công thức cơ bản và quan trọng nhất về elip:
CÔNG THỨC CHÍNH TẮC:
$$\boxed{\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad (a > b > 0)}$$
Trong đó:
- $x$, $y$: tọa độ điểm trên elip
- $a$: bán trục lớn (theo trục $Ox$)
- $b$: bán trục nhỏ (theo trục $Oy$)
- Tâm elip tại gốc tọa độ $O(0; 0)$
Điều kiện bắt buộc: $a > b > 0$
Ý nghĩa:
- Phân số bên trái luôn có giá trị bằng 1
- Mọi điểm $(x, y)$ thỏa mãn phương trình này đều nằm trên elip
- Ngược lại, mọi điểm trên elip đều thỏa mãn phương trình
Dạng khai triển: $$b^2x^2 + a^2y^2 = a^2b^2$$
2. Hệ thức cơ bản giữa a, b, c
Đây là hệ thức quan trọng thứ hai, liên hệ giữa các đại lượng cơ bản:
CÔNG THỨC QUAN TRỌNG:
$$\boxed{c^2 = a^2 – b^2}$$
hoặc viết theo dạng khác:
$$\boxed{a^2 = b^2 + c^2}$$
Trong đó:
- $c$: tiêu cự (khoảng cách từ tâm $O$ đến mỗi tiêu điểm)
- Tiêu điểm: $F_1(-c; 0)$ và $F_2(c; 0)$
Cách ghi nhớ: Công thức này giống định lý Pythagore:
- Trong tam giác vuông: $c^2 = a^2 + b^2$
- Trong elip: $c^2 = a^2 – b^2$ (dấu trừ thay vì cộng)
- Hoặc nhớ: “$a$ bình = $b$ bình cộng $c$ bình”
Hệ quả:
- $c = \sqrt{a^2 – b^2}$ (tính $c$ khi biết $a$ và $b$)
- $b = \sqrt{a^2 – c^2}$ (tính $b$ khi biết $a$ và $c$)
- $a = \sqrt{b^2 + c^2}$ (tính $a$ khi biết $b$ và $c$)
3. Cách xác định phương trình elip
Quy trình 3 bước:
Bước 1: Xác định $a$ và $b$
- $a$ là bán trục lớn (số lớn hơn)
- $b$ là bán trục nhỏ (số nhỏ hơn)
- Luôn có: $a > b > 0$
Bước 2: Tính bình phương
- $a^2$ và $b^2$
Bước 3: Viết phương trình
- $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$
Ví dụ 1: Viết phương trình chính tắc của elip có $a = 5$ và $b = 3$
Lời giải:
Bước 1: Xác định
- Bán trục lớn: $a = 5$
- Bán trục nhỏ: $b = 3$
Bước 2: Tính bình phương
- $a^2 = 25$
- $b^2 = 9$
Bước 3: Viết phương trình $$\boxed{\frac{x^2}{25} + \frac{y^2}{9} = 1}$$
Ví dụ 2: Cho elip có phương trình $\frac{x^2}{16} + \frac{y^2}{9} = 1$. Xác định $a$, $b$, $c$ và tọa độ tiêu điểm.
Lời giải:
Bước 1: Xác định $a$ và $b$
- $a^2 = 16 \Rightarrow a = 4$
- $b^2 = 9 \Rightarrow b = 3$
Bước 2: Tính $c$ $$c^2 = a^2 – b^2 = 16 – 9 = 7$$ $$c = \sqrt{7} \approx 2.65$$
Bước 3: Tọa độ tiêu điểm
- $F_1(-\sqrt{7}; 0)$
- $F_2(\sqrt{7}; 0)$
Kiểm tra: $a = 4 > b = 3$ ✓ và $c = \sqrt{7} < a = 4$ ✓
Ví dụ 3: Lập phương trình elip biết $a = 6$ và $c = 4$
Lời giải:
Bước 1: Tính $b$ từ hệ thức cơ bản $$b^2 = a^2 – c^2 = 36 – 16 = 20$$ $$b = \sqrt{20} = 2\sqrt{5}$$
Bước 2: Viết phương trình $$\boxed{\frac{x^2}{36} + \frac{y^2}{20} = 1}$$
4. Trường hợp đặc biệt: Trục lớn theo Oy
Trong một số trường hợp, trục lớn của elip nằm theo trục tung $Oy$ thay vì trục hoành $Ox$.
Phương trình khi trục lớn theo $Oy$:
$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad (b > a > 0)$$
Lưu ý: Điều kiện đổi thành $b > a$ (thay vì $a > b$)
Đặc điểm:
- Tiêu điểm nằm trên trục $Oy$: $F_1(0; -c)$ và $F_2(0; c)$
- Với $c^2 = b^2 – a^2$ (chú ý: $b^2$ trừ $a^2$)
- Trục lớn: $2b$ (theo $Oy$)
- Trục nhỏ: $2a$ (theo $Ox$)
Quy tắc chung để nhận biết:
Trục lớn luôn nằm dưới mẫu số lớn hơn trong phương trình
Ví dụ:
- $\frac{x^2}{25} + \frac{y^2}{16} = 1$: Trục lớn theo $Ox$ (vì $25 > 16$)
- $\frac{x^2}{9} + \frac{y^2}{25} = 1$: Trục lớn theo $Oy$ (vì $25 > 9$)
III. CÔNG THỨC DIỆN TÍCH ELIP ⭐
1. Công thức tính diện tích
Đây là công thức quan trọng và hay sử dụng nhất về elip:
CÔNG THỨC DIỆN TÍCH:
$$\boxed{S = \pi ab}$$
Trong đó:
- $S$: diện tích hình elip (đơn vị: đơn vị diện tích)
- $a$: bán trục lớn
- $b$: bán trục nhỏ
- $\pi \approx 3.14159$ (hằng số pi)
Cách nhớ: “Pi nhân hai bán trục”
Công thức này tương tự công thức diện tích hình tròn $S = \pi r^2 = \pi r \cdot r$, nhưng thay hai bán kính giống nhau thành hai bán trục khác nhau.
So sánh với đường tròn:
| Hình | Công thức diện tích |
|---|---|
| Đường tròn | $S = \pi r^2 = \pi r \cdot r$ |
| Elip | $S = \pi a \cdot b$ |
Khi $a = b = r$, elip trở thành đường tròn và công thức diện tích trùng nhau.
2. Ví dụ minh họa
Ví dụ 1: Tính diện tích elip có $a = 5$ và $b = 3$
Lời giải:
Áp dụng công thức: $$S = \pi \cdot 5 \cdot 3 = 15\pi$$
Giá trị xấp xỉ: $$S \approx 15 \times 3.14159 \approx \boxed{47.12 \text{ đvdt}}$$
Ví dụ 2: Elip có phương trình $\frac{x^2}{16} + \frac{y^2}{9} = 1$. Tính diện tích.
Lời giải:
Bước 1: Xác định $a$ và $b$
- $a^2 = 16 \Rightarrow a = 4$
- $b^2 = 9 \Rightarrow b = 3$
Bước 2: Tính diện tích $$S = \pi \cdot 4 \cdot 3 = \boxed{12\pi}$$
Hoặc: $S \approx 37.7$ đơn vị diện tích
Ví dụ 3: Elip có trục lớn dài 10 và trục nhỏ dài 6. Tính diện tích.
Lời giải:
Bước 1: Từ độ dài trục tính bán trục
- Trục lớn $2a = 10 \Rightarrow a = 5$
- Trục nhỏ $2b = 6 \Rightarrow b = 3$
Bước 2: Tính diện tích $$S = \pi \cdot 5 \cdot 3 = \boxed{15\pi \approx 47.12 \text{ đvdt}}$$
Ví dụ 4: Elip có $a = 8$, $c = 6$. Tính diện tích.
Lời giải:
Bước 1: Tính $b$ $$b^2 = a^2 – c^2 = 64 – 36 = 28$$ $$b = \sqrt{28} = 2\sqrt{7}$$
Bước 2: Tính diện tích $$S = \pi \cdot 8 \cdot 2\sqrt{7} = \boxed{16\sqrt{7}\pi \approx 132.9 \text{ đvdt}}$$
3. Ứng dụng thực tế
Bài toán 1: Thiết kế sân vườn
Một khu vườn có hình dạng elip với trục lớn dài 20 mét và trục nhỏ dài 12 mét. Tính diện tích của khu vườn.
Lời giải:
Bước 1: Xác định bán trục
- Trục lớn $2a = 20$ m $\Rightarrow a = 10$ m
- Trục nhỏ $2b = 12$ m $\Rightarrow b = 6$ m
Bước 2: Tính diện tích $$S = \pi \cdot 10 \cdot 6 = 60\pi \approx \boxed{188.5 \text{ m}^2}$$
Ứng dụng: Tính toán lượng đất cần san lấp, số lượng cỏ cần trồng, chi phí làm vườn.
Bài toán 2: Tính diện tích ao nước
Một ao nước hình elip có bán trục lớn $a = 8$ m và bán trục nhỏ $b = 5$ m. Tính diện tích mặt nước.
Lời giải:
$$S = \pi \cdot 8 \cdot 5 = \boxed{40\pi \approx 125.66 \text{ m}^2}$$
Ứng dụng: Ước tính lượng nước chứa, số lượng cá có thể thả, chi phí làm ao.
Bài toán 3: Thiết kế quảng trường
Một quảng trường hình elip có phương trình $\frac{x^2}{900} + \frac{y^2}{400} = 1$ (đơn vị: mét). Tính diện tích quảng trường.
Lời giải:
Bước 1: Xác định $a$ và $b$
- $a^2 = 900 \Rightarrow a = 30$ m
- $b^2 = 400 \Rightarrow b = 20$ m
Bước 2: Tính diện tích $$S = \pi \cdot 30 \cdot 20 = 600\pi \approx \boxed{1885 \text{ m}^2}$$
Ứng dụng: Quy hoạch không gian, tính toán số người có thể chứa, thiết kế hệ thống chiếu sáng.
IV. CÔNG THỨC CHU VI ELIP
1. Công thức gần đúng
Khác với đường tròn, chu vi elip không có công thức chính xác đơn giản. Để tính chu vi elip cần dùng tích phân elliptic phức tạp. Trong thực tế, người ta sử dụng các công thức xấp xỉ.
Công thức Ramanujan (Chính xác nhất):
$$\boxed{C \approx \pi\left[3(a+b) – \sqrt{(3a+b)(a+3b)}\right]}$$
Đây là công thức cho kết quả chính xác nhất, sai số rất nhỏ.
Công thức đơn giản hơn:
$$\boxed{C \approx \pi\sqrt{2(a^2 + b^2)}}$$
Công thức này dễ nhớ hơn, sai số chấp nhận được.
Công thức đơn giản thứ ba:
$$\boxed{C \approx 2\pi\sqrt{\frac{a^2 + b^2}{2}}}$$
Tương đương với công thức trên, chỉ khác cách viết.
Công thức đơn giản nhất (Sai số lớn):
$$\boxed{C \approx \pi(a + b)}$$
Công thức này đơn giản nhất nhưng chỉ chính xác khi $a$ và $b$ gần bằng nhau. Sai số lớn khi $a$ và $b$ chênh lệch nhiều.
2. Ví dụ so sánh các công thức
Ví dụ: Elip có $a = 5$ và $b = 3$. Tính chu vi bằng các công thức khác nhau và so sánh.
Lời giải:
Công thức 1: Ramanujan (chính xác nhất)
$$C \approx \pi[3(5+3) – \sqrt{(3 \times 5+3)(5+3 \times 3)}]$$ $$= \pi[3 \times 8 – \sqrt{(15+3)(5+9)}]$$ $$= \pi[24 – \sqrt{18 \times 14}]$$ $$= \pi[24 – \sqrt{252}]$$ $$\approx \pi[24 – 15.87]$$ $$\approx \pi \times 8.13$$ $$\approx \boxed{25.53}$$
Công thức 2: Đơn giản
$$C \approx \pi\sqrt{2(a^2 + b^2)}$$ $$= \pi\sqrt{2(25 + 9)}$$ $$= \pi\sqrt{68}$$ $$\approx \pi \times 8.25$$ $$\approx \boxed{25.93}$$
Công thức 3: Đơn giản nhất
$$C \approx \pi(a + b)$$ $$= \pi(5 + 3)$$ $$= 8\pi$$ $$\approx \boxed{25.13}$$
So sánh kết quả:
- Ramanujan: 25.53
- Công thức đơn giản: 25.93
- Công thức đơn giản nhất: 25.13
Kết luận: Công thức Ramanujan cho kết quả chính xác nhất. Các công thức khác có sai số nhưng dễ tính hơn.
3. Lưu ý quan trọng
⚠️ CHÚ Ý QUAN TRỌNG:
- Chu vi elip KHÔNG có công thức đơn giản như đường tròn ($C = 2\pi r$)
- Trong các kỳ thi THPT Quốc gia, thường KHÔNG yêu cầu tính chu vi elip
- Nếu đề bài yêu cầu tính chu vi, thường sẽ:
- Cho sẵn công thức cần dùng
- Hoặc yêu cầu dùng công thức gần đúng đơn giản
- Hoặc cho trước giá trị chu vi để tính ngược
- Trọng tâm học tập: Tập trung vào diện tích (công thức $S = \pi ab$) vì đây là công thức hay gặp và quan trọng nhất
V. TÂM SAI CỦA ELIP
1. Định nghĩa tâm sai
Tâm sai (hay độ lệch tâm, eccentricity) là một đại lượng đặc trưng cho “hình dạng” của elip – đo mức độ “dẹt” của elip.
CÔNG THỨC TÂM SAI:
$$\boxed{e = \frac{c}{a}}$$
Trong đó:
- $e$: tâm sai (ký hiệu từ chữ eccentricity)
- $c$: tiêu cự (khoảng cách từ tâm đến tiêu điểm)
- $a$: bán trục lớn
Điều kiện: $0 < e < 1$ (luôn luôn)
Giải thích điều kiện:
- Vì $c < a$ (tiêu điểm nằm bên trong elip)
- Nên $\frac{c}{a} < 1$
- Và vì $c > 0$ nên $e > 0$
2. Ý nghĩa của tâm sai
Tâm sai cho biết elip “dẹt” hay “tròn”:
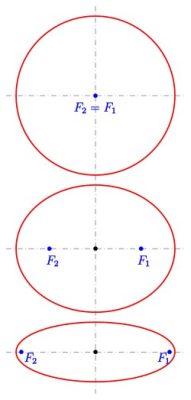
Khi $e$ gần 0:
- $c$ rất nhỏ (tiêu điểm gần tâm)
- $a \approx b$ (hai bán trục gần bằng nhau)
- Elip gần giống đường tròn
Khi $e$ gần 1:
- $c$ gần bằng $a$ (tiêu điểm gần đỉnh)
- $b$ rất nhỏ so với $a$
- Elip rất dẹt
Trường hợp đặc biệt:
- $e = 0$: $c = 0$ → $a = b$ → Đường tròn
- $e = 1$: $c = a$ → $b = 0$ → Elip suy biến thành đoạn thẳng
Minh họa trực quan:
e ≈ 0.1 e ≈ 0.5 e ≈ 0.9
● ⚪ ─
(Gần tròn) (Elip) (Rất dẹt)
3. Công thức liên quan đến tâm sai
Từ $c^2 = a^2 – b^2$ và $e = \frac{c}{a}$, ta có:
Công thức 1: $$c = ea$$
Công thức 2: $$\boxed{b^2 = a^2(1 – e^2)}$$
hoặc
$$b = a\sqrt{1 – e^2}$$
Công thức 3: $$\boxed{e = \sqrt{1 – \frac{b^2}{a^2}}}$$
hoặc
$$e^2 = 1 – \frac{b^2}{a^2} = \frac{a^2 – b^2}{a^2}$$
4. Ví dụ minh họa
Ví dụ 1: Elip có $a = 5$ và $c = 4$. Tính tâm sai.
Lời giải:
Áp dụng công thức trực tiếp: $$e = \frac{c}{a} = \frac{4}{5} = \boxed{0.8}$$
Nhận xét: $e = 0.8$ khá gần 1, nên elip này khá dẹt.
Ví dụ 2: Elip có $a = 10$ và $b = 6$. Tính tâm sai.
Lời giải:
Bước 1: Tính $c$ $$c^2 = a^2 – b^2 = 100 – 36 = 64$$ $$c = 8$$
Bước 2: Tính tâm sai $$e = \frac{c}{a} = \frac{8}{10} = \boxed{0.8}$$
Ví dụ 3: Elip có tâm sai $e = 0.6$ và bán trục lớn $a = 5$. Tính $b$ và $c$.
Lời giải:
Bước 1: Tính $c$ $$c = ea = 0.6 \times 5 = 3$$
Bước 2: Tính $b$ $$b^2 = a^2 – c^2 = 25 – 9 = 16$$ $$b = \boxed{4}$$
Kiểm tra: $a^2 = b^2 + c^2 \Rightarrow 25 = 16 + 9$ ✓
Ví dụ 4: Elip có phương trình $\frac{x^2}{36} + \frac{y^2}{20} = 1$. Tính tâm sai.
Lời giải:
Bước 1: Xác định $a$ và $b$
- $a^2 = 36 \Rightarrow a = 6$
- $b^2 = 20 \Rightarrow b = 2\sqrt{5}$
Bước 2: Tính $c$ $$c^2 = 36 – 20 = 16 \Rightarrow c = 4$$
Bước 3: Tính tâm sai $$e = \frac{4}{6} = \boxed{\frac{2}{3} \approx 0.67}$$
5. Tâm sai quỹ đạo hành tinh
Trong thiên văn học, quỹ đạo hành tinh quay quanh Mặt Trời là elip với Mặt Trời ở một tiêu điểm. Tâm sai cho biết quỹ đạo “tròn” hay “dẹt”:
| Hành tinh | Tâm sai $e$ | Đánh giá độ dẹt |
|---|---|---|
| Sao Kim | 0.007 | Gần như tròn hoàn hảo |
| Trái Đất | 0.017 | Gần tròn |
| Sao Hỏa | 0.093 | Hơi dẹt |
| Sao Thủy | 0.206 | Khá dẹt |
| Sao Diêm Vương | 0.249 | Rất dẹt |
Nhận xét:
- Hầu hết hành tinh có quỹ đạo gần tròn ($e$ nhỏ)
- Sao Thủy và Sao Diêm Vương có quỹ đạo dẹt hơn
- Trái Đất có quỹ đạo rất gần tròn ($e = 0.017 \approx 0$)
VI. CÁC CÔNG THỨC KHÁC VỀ ELIP
1. Phương trình tiếp tuyến
Định nghĩa: Tiếp tuyến của elip tại điểm $M$ là đường thẳng chỉ có một điểm chung với elip tại $M$.
Công thức tiếp tuyến tại điểm $M(x_0; y_0)$:
Cho elip $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ và điểm $M(x_0; y_0)$ nằm trên elip.
Phương trình tiếp tuyến tại $M$:
$$\boxed{\frac{x \cdot x_0}{a^2} + \frac{y \cdot y_0}{b^2} = 1}$$
Cách nhớ: Thay $x^2$ thành $x \cdot x_0$ và $y^2$ thành $y \cdot y_0$ trong phương trình elip.
Ví dụ: Viết phương trình tiếp tuyến của elip $\frac{x^2}{25} + \frac{y^2}{16} = 1$ tại điểm $M(3; \frac{16}{5})$
Lời giải:
Bước 1: Kiểm tra $M$ có thuộc elip không $$\frac{9}{25} + \frac{256/25}{16} = \frac{9}{25} + \frac{16}{25} = 1$$ ✓
Bước 2: Áp dụng công thức tiếp tuyến $$\frac{3x}{25} + \frac{\frac{16}{5} \cdot y}{16} = 1$$
$$\frac{3x}{25} + \frac{y}{5} = 1$$
Bước 3: Rút gọn (nhân cả hai vế với 25) $$3x + 5y = 25$$
Kết luận: Phương trình tiếp tuyến: $\boxed{3x + 5y = 25}$
2. Khoảng cách tiêu điểm
Với điểm $M(x; y)$ bất kỳ nằm trên elip, khoảng cách từ $M$ đến hai tiêu điểm được tính theo công thức:
$$\boxed{MF_1 = a + ex}$$
$$\boxed{MF_2 = a – ex}$$
Trong đó $e = \frac{c}{a}$ là tâm sai.
Kiểm tra tính đúng đắn: $$MF_1 + MF_2 = (a + ex) + (a – ex) = 2a$$ ✓
Điều này phù hợp với định nghĩa elip: tổng khoảng cách từ một điểm trên elip đến hai tiêu điểm bằng $2a$.
3. Độ dài dây cung tiêu
Dây cung tiêu (latus rectum) là dây cung đi qua tiêu điểm và vuông góc với trục lớn.
Công thức:
$$\boxed{L = \frac{2b^2}{a}}$$
Ý nghĩa: Đây là độ dài đoạn thẳng qua tiêu điểm, vuông góc với trục chính.
4. Bán kính cong
Bán kính cong tại các đỉnh của elip:
Tại đỉnh trên trục lớn ($x = \pm a, y = 0$): $$\boxed{\rho_{\max} = \frac{b^2}{a}}$$
Tại đỉnh trên trục nhỏ ($x = 0, y = \pm b$): $$\boxed{\rho_{\min} = \frac{a^2}{b}}$$
Ý nghĩa: Bán kính cong cho biết elip “cong” nhiều hay ít tại các vị trí khác nhau.
VII. BẢNG TỔNG HỢP CÔNG THỨC ⭐
Bảng 1: Công thức cơ bản (Quan trọng nhất)
| Đại lượng | Công thức | Ghi chú |
|---|---|---|
| Phương trình chính tắc | $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ | $a > b > 0$ |
| Hệ thức cơ bản | $c^2 = a^2 – b^2$ | hoặc $a^2 = b^2 + c^2$ |
| DIỆN TÍCH | $\boxed{S = \pi ab}$ | ⭐ Quan trọng nhất! |
| Chu vi (gần đúng) | $C \approx \pi\sqrt{2(a^2 + b^2)}$ | Công thức xấp xỉ |
| Tâm sai | $e = \frac{c}{a}$ | $0 < e < 1$ |
| Tiêu điểm | $F_1(-c; 0), F_2(c; 0)$ | Trên trục $Ox$ |
| Trục lớn | $2a$ | Theo $Ox$ |
| Trục nhỏ | $2b$ | Theo $Oy$ |
| Các đỉnh | $(\pm a; 0), (0; \pm b)$ | 4 đỉnh |
Bảng 2: Mối quan hệ giữa các đại lượng
| Cho trước | Tính được | Công thức |
|---|---|---|
| $a, b$ | $c$ | $c = \sqrt{a^2 – b^2}$ |
| $a, c$ | $b$ | $b = \sqrt{a^2 – c^2}$ |
| $b, c$ | $a$ | $a = \sqrt{b^2 + c^2}$ |
| $a, e$ | $c, b$ | $c = ae$; $b = a\sqrt{1-e^2}$ |
| $a, b$ | $e$ | $e = \frac{\sqrt{a^2-b^2}}{a}$ |
| $a, b$ | $S$ | $S = \pi ab$ |
Bảng 3: Trường hợp đặc biệt
| Điều kiện | Loại đường cong | Đặc điểm |
|---|---|---|
| $a = b = r$ | Đường tròn | $e = 0$, $c = 0$ |
| $b \to 0$ | Đoạn thẳng | $e \to 1$, elip suy biến |
| $e \to 0$ | Gần đường tròn | $c \to 0$, $a \approx b$ |
| $e \to 1$ | Elip rất dẹt | $c \to a$, $b \to 0$ |
Bảng 4: Công thức bổ sung
| Công thức | Ý nghĩa |
|---|---|
| $MF_1 + MF_2 = 2a$ | Định nghĩa elip |
| $\frac{x \cdot x_0}{a^2} + \frac{y \cdot y_0}{b^2} = 1$ | Tiếp tuyến tại $M(x_0; y_0)$ |
| $MF_1 = a + ex$ | Khoảng cách đến tiêu điểm 1 |
| $MF_2 = a – ex$ | Khoảng cách đến tiêu điểm 2 |
| $L = \frac{2b^2}{a}$ | Dây cung tiêu |
VIII. BÀI TẬP MẪU
Dạng 1: Lập phương trình elip
Bài tập 1: Lập phương trình chính tắc của elip biết $a = 5$ và $b = 4$
Lời giải:
Áp dụng công thức phương trình chính tắc: $$\boxed{\frac{x^2}{25} + \frac{y^2}{16} = 1}$$
Bài tập 2: Lập phương trình elip biết bán trục lớn $a = 5$ và tiêu cự $c = 3$
Lời giải:
Bước 1: Tính $b$ $$b^2 = a^2 – c^2 = 25 – 9 = 16$$ $$b = 4$$
Bước 2: Viết phương trình $$\boxed{\frac{x^2}{25} + \frac{y^2}{16} = 1}$$
Bài tập 3: Lập phương trình elip đi qua điểm $M(3; 2)$ và $N(4; 0)$
Lời giải:
Bước 1: Từ $N(4; 0)$ nằm trên elip $$\frac{16}{a^2} + \frac{0}{b^2} = 1 \Rightarrow a^2 = 16 \Rightarrow a = 4$$
Bước 2: Từ $M(3; 2)$ nằm trên elip $$\frac{9}{16} + \frac{4}{b^2} = 1$$ $$\frac{4}{b^2} = 1 – \frac{9}{16} = \frac{7}{16}$$ $$b^2 = \frac{64}{7}$$
Bước 3: Phương trình $$\boxed{\frac{x^2}{16} + \frac{7y^2}{64} = 1}$$
Dạng 2: Tính diện tích elip
Bài tập 4: Elip có phương trình $\frac{x^2}{36} + \frac{y^2}{16} = 1$. Tính diện tích.
Lời giải:
Bước 1: Xác định $a$ và $b$
- $a^2 = 36 \Rightarrow a = 6$
- $b^2 = 16 \Rightarrow b = 4$
Bước 2: Tính diện tích $$S = \pi \cdot 6 \cdot 4 = \boxed{24\pi \approx 75.4 \text{ đvdt}}$$
Bài tập 5: Elip có trục lớn dài 14 và trục nhỏ dài 10. Tính diện tích.
Lời giải:
Bước 1: Tính bán trục
- $2a = 14 \Rightarrow a = 7$
- $2b = 10 \Rightarrow b = 5$
Bước 2: Tính diện tích $$S = 7 \times 5 \times \pi = \boxed{35\pi \approx 110 \text{ đvdt}}$$
Dạng 3: Tính tâm sai
Bài tập 6: Elip $\frac{x^2}{25} + \frac{y^2}{9} = 1$. Tính tâm sai và tọa độ tiêu điểm.
Lời giải:
Bước 1: Xác định $a$ và $b$
- $a = 5$, $b = 3$
Bước 2: Tính $c$ $$c = \sqrt{25 – 9} = \sqrt{16} = 4$$
Bước 3: Tính tâm sai $$e = \frac{4}{5} = \boxed{0.8}$$
Bước 4: Tọa độ tiêu điểm
- $F_1(-4; 0)$ và $F_2(4; 0)$
Bài tập 7: Elip có tâm sai $e = 0.5$ và bán trục lớn $a = 10$. Tính $b$, $c$ và diện tích.
Lời giải:
Bước 1: Tính $c$ $$c = ea = 0.5 \times 10 = 5$$
Bước 2: Tính $b$ $$b^2 = a^2 – c^2 = 100 – 25 = 75$$ $$b = \sqrt{75} = 5\sqrt{3}$$
Bước 3: Tính diện tích $$S = 10 \times 5\sqrt{3} \times \pi = \boxed{50\sqrt{3}\pi \approx 272 \text{ đvdt}}$$
Dạng 4: Tìm điểm trên elip
Bài tập 8: Cho elip $\frac{x^2}{16} + \frac{y^2}{9} = 1$. Tìm tọa độ điểm $M$ trên elip có hoành độ $x = 2$.
Lời giải:
Thay $x = 2$ vào phương trình elip: $$\frac{4}{16} + \frac{y^2}{9} = 1$$ $$\frac{1}{4} + \frac{y^2}{9} = 1$$ $$\frac{y^2}{9} = \frac{3}{4}$$ $$y^2 = \frac{27}{4}$$ $$y = \pm\frac{3\sqrt{3}}{2}$$
Kết luận: Có 2 điểm thỏa mãn:
- $M_1\left(2; \frac{3\sqrt{3}}{2}\right)$
- $M_2\left(2; -\frac{3\sqrt{3}}{2}\right)$
Dạng 5: Bài toán tổng hợp
Bài tập 9: Elip có phương trình $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ đi qua điểm $A(2; 3)$ và có tâm sai $e = \frac{1}{2}$. a) Tìm $a$ và $b$ b) Tính diện tích elip
Lời giải:
Câu a:
Từ $e = \frac{1}{2}$: $$\frac{c}{a} = \frac{1}{2} \Rightarrow c = \frac{a}{2}$$
Từ $c^2 = a^2 – b^2$: $$\frac{a^2}{4} = a^2 – b^2$$ $$b^2 = \frac{3a^2}{4}$$
Từ $A(2; 3)$ thuộc elip: $$\frac{4}{a^2} + \frac{9}{b^2} = 1$$ $$\frac{4}{a^2} + \frac{9}{\frac{3a^2}{4}} = 1$$ $$\frac{4}{a^2} + \frac{12}{a^2} = 1$$ $$\frac{16}{a^2} = 1$$ $$a^2 = 16 \Rightarrow a = 4$$
$$b^2 = \frac{3 \times 16}{4} = 12 \Rightarrow b = 2\sqrt{3}$$
Câu b: $$S = \pi \times 4 \times 2\sqrt{3} = \boxed{8\sqrt{3}\pi}$$
IX. KẾT LUẬN
Trong tất cả các công thức về elip, có 4 công thức cốt lõi cần nhớ:
1. Phương trình chính tắc: $$\boxed{\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad (a > b > 0)}$$
2. Hệ thức cơ bản: $$\boxed{c^2 = a^2 – b^2}$$ hoặc $$\boxed{a^2 = b^2 + c^2}$$
3. DIỆN TÍCH (Quan trọng nhất!): $$\boxed{S = \pi ab}$$ ⭐⭐⭐
4. Tâm sai: $$\boxed{e = \frac{c}{a}}$$
Quy tắc vàng khi làm bài tập
Bước 1: Nhận dạng
- $a$ là bán trục lớn (số lớn hơn)
- $b$ là bán trục nhỏ (số nhỏ hơn)
- Luôn kiểm tra: $a > b > 0$
Bước 2: Tính $c$
- Sử dụng: $c^2 = a^2 – b^2$
- Hoặc: $c = \sqrt{a^2 – b^2}$
Bước 3: Tính diện tích
- Áp dụng: $S = \pi ab$
- Nhân hai bán trục với $\pi$
Bước 4: Tính tâm sai (nếu cần)
- Công thức: $e = \frac{c}{a}$
- Kiểm tra: $0 < e < 1$
Các chủ đề liên quan:
- Phương trình đường tròn
- Phương trình parabol
- Phương trình hyperbol
- Hệ tọa độ trong mặt phẳng
- Tích phân tính diện tích

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
