Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ VECTƠ
- 1. Vectơ là gì?
- 2. Các khái niệm cơ bản
- 3. Cấu trúc bài viết
- II. CÁC PHÉP TOÁN VỚI VECTƠ
- 1. Phép cộng vectơ
- 2. Phép trừ vectơ
- 3. Phép nhân vectơ với một số
- 4. Điều kiện hai vectơ cùng phương
- III. PHÂN TÍCH VECTƠ VÀ CÁC QUY TẮC ĐỘC LẬP
- 1. Điều kiện đồng phẳng của ba vectơ
- 2. Quy tắc trung điểm
- 3. Quy tắc trọng tâm tam giác
- 4. Công thức chia đoạn thẳng
- IV. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
- 1. Định nghĩa tích vô hướng
- 2. Các công thức tính tích vô hướng
- 3. Tính chất của tích vô hướng
- 4. Điều kiện vuông góc
- 5. Công thức tính góc giữa hai vectơ
- 6. Công thức tính độ dài vectơ
- V. TỌA ĐỘ VECTƠ TRONG MẶT PHẲNG
- 1. Hệ trục tọa độ Oxy
- 2. Tọa độ của vectơ
- 3. Tọa độ của điểm
- 4. Công thức tọa độ cơ bản
- 5. Các phép toán với tọa độ vectơ
- 6. Điều kiện đặc biệt theo tọa độ
- VI. ỨNG DỤNG VECTƠ TRONG HÌNH HỌC
- 1. Chứng minh ba điểm thẳng hàng
- 2. Chứng minh tứ giác là hình bình hành
- 3. Chứng minh hai đường thẳng vuông góc
- 4. Tính góc trong tam giác
- 5. Chứng minh đẳng thức hình học
- VII. BẢNG TÓM TẮT CÔNG THỨC
- A. Phép toán vectơ
- B. Tích vô hướng
- C. Tọa độ vectơ
- D. Công thức đặc biệt
- VIII. KẾT LUẬN
- Tổng kết kiến thức
I. GIỚI THIỆU VỀ VECTƠ
1. Vectơ là gì?
Định nghĩa:
Vectơ là một đại lượng có cả độ lớn (module) và hướng, được biểu diễn bằng một đoạn thẳng có hướng từ điểm đầu đến điểm cuối.
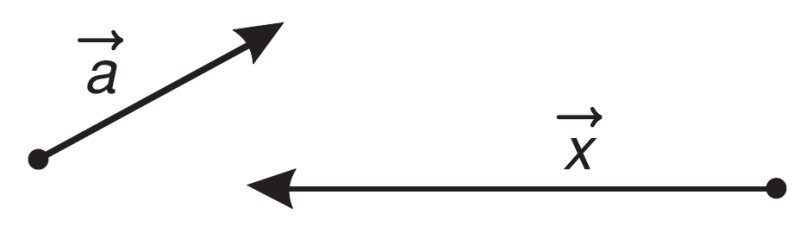
Ký hiệu chuẩn:
- Vectơ tổng quát: $\vec{a}$, $\vec{b}$, $\vec{c}$, $\vec{u}$, $\vec{v}$
- Vectơ nối hai điểm: $\vec{AB}$, $\vec{CD}$, $\vec{MN}$
- Điểm A: điểm đầu
- Điểm B: điểm cuối
- Độ dài (module): $|\vec{a}|$ hoặc $a$
- Độ dài đoạn thẳng: $AB = |\vec{AB}|$
Ví dụ thực tế dễ hiểu:
- Lực: Khi đẩy một vật, lực có độ lớn (10N, 20N,…) và hướng tác dụng (sang phải, lên trên,…)
- Vận tốc: Xe chạy 60 km/h (độ lớn) theo hướng Đông (hướng)
- Chuyển dời: Đi từ nhà (A) đến trường (B), có khoảng cách (độ dài) và hướng đi
- Gió: Gió mạnh 15 m/s thổi theo hướng Tây Nam
Phân biệt rõ ràng:
| Đại lượng vô hướng | Đại lượng có hướng (Vectơ) |
|---|---|
| Chỉ có độ lớn | Có cả độ lớn và hướng |
| Khối lượng: 5 kg | Lực: 10N hướng Đông |
| Nhiệt độ: 25°C | Vận tốc: 60 km/h hướng Bắc |
| Thời gian: 2 giờ | Chuyển dời: 3 km về phía Nam |
| Điện áp: 220V | Điện trường: có cường độ và hướng |
2. Các khái niệm cơ bản
A. Vectơ không
Ký hiệu: $\vec{0}$
Định nghĩa: Vectơ có độ dài bằng 0, không xác định hướng.
Ví dụ: $\vec{AA} = \vec{0}$ (vectơ từ A đến chính A)
B. Hai vectơ bằng nhau
Điều kiện: $\vec{a} = \vec{b}$ khi và chỉ khi:
- Cùng độ dài: $|\vec{a}| = |\vec{b}|$
- Cùng hướng
Chú ý: Hai vectơ bằng nhau không nhất thiết trùng nhau về vị trí.
Ví dụ: Trong hình bình hành ABCD: $\vec{AB} = \vec{DC}$ (cùng độ dài, cùng hướng)
C. Vectơ đối
Định nghĩa: $\vec{a}$ và $-\vec{a}$ là hai vectơ đối khi:
- Cùng độ dài: $|\vec{a}| = |-\vec{a}|$
- Ngược hướng
Ví dụ: $\vec{AB}$ và $\vec{BA}$ là hai vectơ đối: $\vec{BA} = -\vec{AB}$
D. Vectơ cùng phương
Định nghĩa: Hai vectơ cùng phương khi giá của chúng song song hoặc trùng nhau.
Ký hiệu: $\vec{a}$ // $\vec{b}$
Phân loại:
- Cùng hướng: $\vec{a} \uparrow\uparrow \vec{b}$ (cùng phương, cùng chiều)
- Ngược hướng: $\vec{a} \uparrow\downarrow \vec{b}$ (cùng phương, ngược chiều)
Ví dụ:
- Ba điểm A, B, C thẳng hàng → $\vec{AB}$ và $\vec{AC}$ cùng phương
- Hai cạnh đối của hình bình hành → vectơ cùng phương
3. Cấu trúc bài viết
Bài viết này sẽ hệ thống hóa toàn bộ kiến thức vectơ lớp 10:
- Các phép toán vectơ – Cộng, trừ, nhân với số
- Phân tích vectơ – Quy tắc trung điểm, trọng tâm
- Tích vô hướng – Định nghĩa, tính chất, ứng dụng
- Tọa độ vectơ – Hệ trục Oxy, công thức tọa độ
- Ứng dụng hình học – Chứng minh, tính toán cụ thể
- Bảng công thức tổng hợp – Tra cứu nhanh
II. CÁC PHÉP TOÁN VỚI VECTƠ
1. Phép cộng vectơ
Phép cộng vectơ có hai quy tắc cơ bản:
A. Quy tắc hình bình hành
Nội dung: Cho hai vectơ $\vec{AB}$ và $\vec{AC}$ (có chung điểm đầu A). Dựng hình bình hành ABDC, ta có:
$$\boxed{\vec{AB} + \vec{AC} = \vec{AD}}$$
Hình minh họa:
D ←---------- C
↑ ↑
AD | | AC
| |
A ----------→ B
AB
Giải thích: Vectơ tổng là đường chéo xuất phát từ điểm đầu chung.
B. Quy tắc ba điểm (Quy tắc cộng dây chuyền)
Nội dung: Với ba điểm A, B, C bất kỳ:
$$\boxed{\vec{AB} + \vec{BC} = \vec{AC}}$$
Quy tắc nhớ: “Điểm cuối nối điểm đầu”
Giải thích: Đi từ A đến B, rồi từ B đến C, kết quả là đi từ A đến C.
C. Quy tắc chuỗi (Mở rộng cho n điểm)
Với dãy điểm $A_1, A_2, A_3, …, A_n$:
$$\boxed{\vec{A_1A_2} + \vec{A_2A_3} + \vec{A_3A_4} + \ldots + \vec{A_{n-1}A_n} = \vec{A_1A_n}}$$
Ví dụ: $$\vec{AB} + \vec{BC} + \vec{CD} + \vec{DE} = \vec{AE}$$
Quy tắc: Các điểm giữa “triệt tiêu” lẫn nhau, chỉ còn điểm đầu và điểm cuối.
D. Tính chất của phép cộng vectơ
| Tính chất | Công thức | Ý nghĩa |
|---|---|---|
| Giao hoán | $\vec{a} + \vec{b} = \vec{b} + \vec{a}$ | Đổi thứ tự không đổi kết quả |
| Kết hợp | $(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})$ | Nhóm nào trước cũng được |
| Phần tử trung hòa | $\vec{a} + \vec{0} = \vec{a}$ | Cộng với vectơ không không thay đổi |
| Phần tử đối | $\vec{a} + (-\vec{a}) = \vec{0}$ | Tổng vectơ đối bằng vectơ không |
2. Phép trừ vectơ
Định nghĩa
$$\boxed{\vec{a} – \vec{b} = \vec{a} + (-\vec{b})}$$
Giải thích: Trừ một vectơ = Cộng với vectơ đối của nó
Quy tắc hiệu vectơ
Công thức quan trọng:
$$\boxed{\vec{AB} – \vec{AC} = \vec{CB}}$$
Quy tắc nhớ: “Hiệu hai vectơ có điểm đầu là điểm cuối của vectơ trừ”
Chứng minh: $$\vec{AB} – \vec{AC} = \vec{AB} + \vec{CA} = \vec{CB}$$
Ví dụ ứng dụng:
- $\vec{OA} – \vec{OB} = \vec{BA}$
- $\vec{MA} – \vec{MB} = \vec{BA}$
- $\vec{PA} – \vec{PB} = \vec{BA}$
Lưu ý: Kết quả không phụ thuộc vào điểm đầu (O, M, hay P đều cho kết quả giống nhau)
3. Phép nhân vectơ với một số
Định nghĩa
Cho số thực $k$ và vectơ $\vec{a} \neq \vec{0}$:
$$\boxed{\vec{b} = k\vec{a}}$$
Tính chất của $\vec{b} = k\vec{a}$:
1. Về độ dài: $$|\vec{b}| = |k| \cdot |\vec{a}|$$
2. Về hướng:
- Nếu $k > 0$: $\vec{b} \uparrow\uparrow \vec{a}$ (cùng hướng với $\vec{a}$)
- Nếu $k < 0$: $\vec{b} \uparrow\downarrow \vec{a}$ (ngược hướng với $\vec{a}$)
- Nếu $k = 0$: $\vec{b} = \vec{0}$ (vectơ không)
Ví dụ minh họa:
- $2\vec{a}$: Vectơ cùng hướng $\vec{a}$, độ dài gấp đôi
- $-3\vec{a}$: Vectơ ngược hướng $\vec{a}$, độ dài gấp 3
- $\frac{1}{2}\vec{a}$: Vectơ cùng hướng $\vec{a}$, độ dài bằng nửa
Tính chất đại số
| Tính chất | Công thức |
|---|---|
| Phân phối với cộng vectơ | $k(\vec{a} + \vec{b}) = k\vec{a} + k\vec{b}$ |
| Phân phối với cộng số | $(m + n)\vec{a} = m\vec{a} + n\vec{a}$ |
| Kết hợp | $(mn)\vec{a} = m(n\vec{a}) = n(m\vec{a})$ |
| Nhân với 1 | $1 \cdot \vec{a} = \vec{a}$ |
| Nhân với -1 | $(-1) \cdot \vec{a} = -\vec{a}$ |
| Nhân với 0 | $0 \cdot \vec{a} = \vec{0}$ |
4. Điều kiện hai vectơ cùng phương
Định lý
Hai vectơ $\vec{a} \neq \vec{0}$ và $\vec{b}$ cùng phương khi và chỉ khi:
$$\boxed{\exists k \in \mathbb{R}: \vec{b} = k\vec{a}}$$
Đọc: “Tồn tại số thực k sao cho vectơ b bằng k nhân vectơ a”
Ứng dụng: Chứng minh ba điểm thẳng hàng
Định lý: Ba điểm A, B, C thẳng hàng khi và chỉ khi:
$$\boxed{\vec{AB} = k\vec{AC} \text{ với } k \in \mathbb{R}}$$
Hoặc tương đương:
$$\boxed{\vec{AB} \text{ và } \vec{AC} \text{ cùng phương}}$$
Ví dụ: Cho A(1; 2), B(3; 4), C(5; 6). Chứng minh A, B, C thẳng hàng?
Lời giải:
- $\vec{AB} = (3-1; 4-2) = (2; 2)$
- $\vec{AC} = (5-1; 6-2) = (4; 4)$
- Ta có: $\vec{AC} = 2\vec{AB}$ với k = 2
→ $\vec{AB}$ và $\vec{AC}$ cùng phương → A, B, C thẳng hàng ✓
III. PHÂN TÍCH VECTƠ VÀ CÁC QUY TẮC ĐỘC LẬP
1. Điều kiện đồng phẳng của ba vectơ
Định lý: Ba vectơ $\vec{a}$, $\vec{b}$, $\vec{c}$ (với $\vec{a}$, $\vec{b}$ không cùng phương) đồng phẳng khi và chỉ khi:
$$\boxed{\exists m, n \in \mathbb{R}: \vec{c} = m\vec{a} + n\vec{b}}$$
Ý nghĩa: Vectơ $\vec{c}$ có thể biểu diễn qua $\vec{a}$ và $\vec{b}$.
Ứng dụng: Phân tích vectơ, chứng minh đồng phẳng.
2. Quy tắc trung điểm
Cho M là trung điểm của đoạn thẳng AB:
Công thức 1:
$$\boxed{\vec{MA} + \vec{MB} = \vec{0}}$$
Hệ quả: $\vec{MA} = -\vec{MB}$
Công thức 2 (Quan trọng nhất):
Với O là điểm bất kỳ trong mặt phẳng:
$$\boxed{\vec{OM} = \frac{\vec{OA} + \vec{OB}}{2}}$$
Cách nhớ: “Tọa độ trung điểm = Trung bình cộng tọa độ hai đầu mút”
Chứng minh:
Từ $\vec{MA} + \vec{MB} = \vec{0}$: $$\vec{OA} – \vec{OM} + \vec{OB} – \vec{OM} = \vec{0}$$ $$\vec{OA} + \vec{OB} = 2\vec{OM}$$ $$\vec{OM} = \frac{\vec{OA} + \vec{OB}}{2}$$
Ví dụ: Cho O(0; 0), A(2; 4), B(6; 8). Tìm tọa độ trung điểm M?
$$\vec{OM} = \frac{\vec{OA} + \vec{OB}}{2} = \frac{(2; 4) + (6; 8)}{2} = \frac{(8; 12)}{2} = (4; 6)$$
Vậy M(4; 6) ✓
3. Quy tắc trọng tâm tam giác
Cho G là trọng tâm tam giác ABC:
Công thức 1 (Tính chất đặc trưng):
$$\boxed{\vec{GA} + \vec{GB} + \vec{GC} = \vec{0}}$$
Ý nghĩa: Tổng ba vectơ từ trọng tâm đến ba đỉnh bằng vectơ không.
Công thức 2 (Biểu diễn qua điểm bất kỳ):
Với O là điểm bất kỳ:
$$\boxed{\vec{OG} = \frac{\vec{OA} + \vec{OB} + \vec{OC}}{3}}$$
Cách nhớ: “Tọa độ trọng tâm = Trung bình cộng tọa độ ba đỉnh chia 3”
Các hệ quả quan trọng:
Hệ quả 1: Biểu diễn $\vec{AG}$ qua hai cạnh:
$$\boxed{\vec{AG} = \frac{1}{3}(\vec{AB} + \vec{AC})}$$
Hệ quả 2: Với M là trung điểm BC:
$$\boxed{\vec{AG} = \frac{2}{3}\vec{AM}}$$
Hoặc: $\vec{MG} = \frac{1}{3}\vec{MA}$
Giải thích: Trọng tâm G chia trung tuyến AM theo tỉ lệ 2:1 (AG = 2GM)
Ví dụ: Cho tam giác ABC có A(0; 3), B(4; 0), C(0; 0). Tìm tọa độ trọng tâm G?
$$\vec{OG} = \frac{\vec{OA} + \vec{OB} + \vec{OC}}{3} = \frac{(0; 3) + (4; 0) + (0; 0)}{3} = \frac{(4; 3)}{3} = \left(\frac{4}{3}; 1\right)$$
Vậy $G\left(\frac{4}{3}; 1\right)$ ✓
4. Công thức chia đoạn thẳng
Cho điểm M chia đoạn thẳng AB theo tỉ số k (k ≠ -1):
Định nghĩa:
$$\boxed{\vec{MA} = k\vec{MB}}$$
Công thức tọa độ M:
Với O là điểm bất kỳ:
$$\boxed{\vec{OM} = \frac{\vec{OA} + k\vec{OB}}{1 + k}}$$
Trường hợp đặc biệt:
- k = 1: M là trung điểm AB $$\vec{OM} = \frac{\vec{OA} + \vec{OB}}{2}$$
- k = 2: M chia AB theo tỉ lệ 2:1 (MA = 2MB) $$\vec{OM} = \frac{\vec{OA} + 2\vec{OB}}{3}$$
- k = -1: Không xác định (M ở vô cực)
Ví dụ: Cho A(1; 2), B(7; 8). Tìm M chia AB theo tỉ lệ 2:1?
$$\vec{OM} = \frac{\vec{OA} + 2\vec{OB}}{3} = \frac{(1; 2) + 2(7; 8)}{3} = \frac{(1; 2) + (14; 16)}{3} = \frac{(15; 18)}{3} = (5; 6)$$
Vậy M(5; 6) ✓
Kiểm tra: MA = 2MB ✓
IV. TÍCH VÔ HƯỚNG CỦA HAI VECTƠ
1. Định nghĩa tích vô hướng
Định nghĩa: Tích vô hướng của hai vectơ $\vec{a}$ và $\vec{b}$ là một số thực, ký hiệu $\vec{a} \cdot \vec{b}$, được tính theo công thức:
$$\boxed{\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos(\vec{a}, \vec{b})}$$
Ký hiệu khác: $\vec{a} \cdot \vec{b}$ hoặc $(\vec{a}, \vec{b})$ hoặc $\langle \vec{a}, \vec{b} \rangle$
Chú ý quan trọng:
- Tích vô hướng cho ra số thực (scalar), KHÔNG phải vectơ
- $(\vec{a}, \vec{b})$ là góc giữa hai vectơ: $0° \leq (\vec{a}, \vec{b}) \leq 180°$
- $\cos(\vec{a}, \vec{b})$ có thể dương, âm, hoặc bằng 0
Giải thích tên gọi: “Vô hướng” vì kết quả là số, không có hướng (khác với tích có hướng trong không gian).
2. Các công thức tính tích vô hướng
A. Công thức cơ bản – Bình phương vectơ
$$\boxed{\vec{a}^2 = \vec{a} \cdot \vec{a} = |\vec{a}|^2}$$
Hệ quả: $$|\vec{a}| = \sqrt{\vec{a}^2}$$
B. Công thức hình chiếu
$$\boxed{\vec{a} \cdot \vec{b} = |\vec{a}| \cdot \text{pr}_{\vec{a}}\vec{b}}$$
Trong đó $\text{pr}_{\vec{a}}\vec{b}$ là độ dài hình chiếu của $\vec{b}$ lên phương của $\vec{a}$.
$$\text{pr}_{\vec{a}}\vec{b} = |\vec{b}| \cdot \cos(\vec{a}, \vec{b})$$
C. Biểu thức theo độ dài các cạnh (Định lý cos)
Trong tam giác ABC:
$$\boxed{\vec{AB} \cdot \vec{AC} = \frac{1}{2}(AB^2 + AC^2 – BC^2)}$$
Chứng minh: Áp dụng định lý cosin: $$BC^2 = AB^2 + AC^2 – 2 \cdot AB \cdot AC \cdot \cos A$$
$$\Rightarrow AB \cdot AC \cdot \cos A = \frac{AB^2 + AC^2 – BC^2}{2}$$
$$\Rightarrow \vec{AB} \cdot \vec{AC} = \frac{1}{2}(AB^2 + AC^2 – BC^2)$$
Ứng dụng: Tính tích vô hướng khi biết độ dài ba cạnh.
3. Tính chất của tích vô hướng
| Tính chất | Công thức | Ghi chú |
|---|---|---|
| Giao hoán | $\vec{a} \cdot \vec{b} = \vec{b} \cdot \vec{a}$ | Đổi vị trí không đổi kết quả |
| Phân phối | $\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}$ | Khai triển như nhân đa thức |
| Kết hợp với số | $(k\vec{a}) \cdot \vec{b} = k(\vec{a} \cdot \vec{b}) = \vec{a} \cdot (k\vec{b})$ | Đưa hệ số ra ngoài |
| Bình phương tổng | $(\vec{a} + \vec{b})^2 = \vec{a}^2 + 2\vec{a} \cdot \vec{b} + \vec{b}^2$ | Giống hằng đẳng thức |
| Bình phương hiệu | $(\vec{a} – \vec{b})^2 = \vec{a}^2 – 2\vec{a} \cdot \vec{b} + \vec{b}^2$ | Giống hằng đẳng thức |
| Hiệu bình phương | $(\vec{a} + \vec{b})(\vec{a} – \vec{b}) = \vec{a}^2 – \vec{b}^2$ | Giống hằng đẳng thức |
Lưu ý: Các hằng đẳng thức vectơ hoàn toàn giống đại số thông thường!
4. Điều kiện vuông góc
Định lý quan trọng:
$$\boxed{\vec{a} \perp \vec{b} \Leftrightarrow \vec{a} \cdot \vec{b} = 0}$$
Chứng minh:
$$\vec{a} \perp \vec{b} \Leftrightarrow (\vec{a}, \vec{b}) = 90° \Leftrightarrow \cos 90° = 0 \Leftrightarrow \vec{a} \cdot \vec{b} = 0$$
Quy ước đặc biệt: $\vec{0} \perp \vec{a}$ với mọi vectơ $\vec{a}$
Ứng dụng: Chứng minh hai đường thẳng vuông góc, tam giác vuông, hình chữ nhật,…
5. Công thức tính góc giữa hai vectơ
Công thức quan trọng:
$$\boxed{\cos(\vec{a}, \vec{b}) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}}$$
Điều kiện: $\vec{a} \neq \vec{0}$, $\vec{b} \neq \vec{0}$
Quy trình tính góc:
- Tính $\vec{a} \cdot \vec{b}$
- Tính $|\vec{a}|$ và $|\vec{b}|$
- Tính $\cos(\vec{a}, \vec{b})$
- Suy ra góc: $(\vec{a}, \vec{b}) = \arccos\left(\frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}\right)$
Ứng dụng: Tính góc giữa hai đường thẳng, góc trong tam giác.
6. Công thức tính độ dài vectơ
Công thức cơ bản:
$$\boxed{|\vec{a}| = \sqrt{\vec{a}^2} = \sqrt{\vec{a} \cdot \vec{a}}}$$
$$\boxed{AB = |\vec{AB}| = \sqrt{\vec{AB}^2}}$$
Công thức khai triển:
Độ dài tổng: $$\boxed{|\vec{a} + \vec{b}|^2 = |\vec{a}|^2 + 2\vec{a} \cdot \vec{b} + |\vec{b}|^2}$$
Độ dài hiệu: $$\boxed{|\vec{a} – \vec{b}|^2 = |\vec{a}|^2 – 2\vec{a} \cdot \vec{b} + |\vec{b}|^2}$$
Ứng dụng: Chứng minh đẳng thức về độ dài, tính khoảng cách.
Ví dụ: Cho $|\vec{a}| = 3$, $|\vec{b}| = 4$, $(\vec{a}, \vec{b}) = 60°$. Tính $|\vec{a} + \vec{b}|$?
Lời giải:
$$\vec{a} \cdot \vec{b} = 3 \cdot 4 \cdot \cos 60° = 12 \cdot \frac{1}{2} = 6$$
$$|\vec{a} + \vec{b}|^2 = |\vec{a}|^2 + 2\vec{a} \cdot \vec{b} + |\vec{b}|^2$$
$$= 9 + 2 \cdot 6 + 16 = 9 + 12 + 16 = 37$$
$$|\vec{a} + \vec{b}| = \sqrt{37}$$
V. TỌA ĐỘ VECTƠ TRONG MẶT PHẲNG
1. Hệ trục tọa độ Oxy
Hệ trục tọa độ Descartes vuông góc: Gồm hai trục số Ox và Oy vuông góc nhau, giao nhau tại gốc O.
Các thành phần:
- Gốc tọa độ: Điểm O
- Trục hoành: Trục Ox (nằm ngang)
- Trục tung: Trục Oy (thẳng đứng)
Vectơ đơn vị:
- $\vec{i}$: Vectơ đơn vị trên trục Ox, $|\vec{i}| = 1$
- $\vec{j}$: Vectơ đơn vị trên trục Oy, $|\vec{j}| = 1$
- $\vec{i} \perp \vec{j}$ (vuông góc nhau)
- $\vec{i} \cdot \vec{j} = 0$
2. Tọa độ của vectơ
Định lý phân tích duy nhất: Mọi vectơ $\vec{a}$ trong mặt phẳng đều phân tích duy nhất thành:
$$\boxed{\vec{a} = x\vec{i} + y\vec{j}}$$
Ký hiệu tọa độ: $\vec{a} = (x; y)$ hoặc $\vec{a}(x; y)$
Trong đó:
- $x$: Hoành độ của vectơ $\vec{a}$ (tọa độ theo trục Ox)
- $y$: Tung độ của vectơ $\vec{a}$ (tọa độ theo trục Oy)
Ví dụ:
- $\vec{i} = (1; 0)$
- $\vec{j} = (0; 1)$
- $\vec{0} = (0; 0)$
- $\vec{a} = 3\vec{i} + 4\vec{j} = (3; 4)$
3. Tọa độ của điểm
Định nghĩa: Điểm M có tọa độ $(x; y)$ khi:
$$\vec{OM} = x\vec{i} + y\vec{j}$$
Ký hiệu: $M(x; y)$ hoặc $M(x, y)$
Ý nghĩa:
- $x$: Khoảng cách có dấu từ M đến trục Oy (hoành độ)
- $y$: Khoảng cách có dấu từ M đến trục Ox (tung độ)
Lưu ý: Tọa độ điểm M chính là tọa độ của vectơ $\vec{OM}$.
4. Công thức tọa độ cơ bản
A. Tọa độ vectơ nối hai điểm
Cho $A(x_A; y_A)$ và $B(x_B; y_B)$:
$$\boxed{\vec{AB} = (x_B – x_A; y_B – y_A)}$$
Quy tắc nhớ: “Điểm cuối trừ điểm đầu”
Ví dụ: A(1; 2), B(5; 7) → $\vec{AB} = (5-1; 7-2) = (4; 5)$
B. Độ dài vectơ (Khoảng cách hai điểm)
$$\boxed{|\vec{AB}| = AB = \sqrt{(x_B – x_A)^2 + (y_B – y_A)^2}}$$
Định lý Pythagore trong tọa độ
Ví dụ: A(1; 2), B(5; 7) → $AB = \sqrt{4^2 + 5^2} = \sqrt{16 + 25} = \sqrt{41}$
C. Tọa độ trung điểm
Cho M là trung điểm của AB:
$$\boxed{M\left(\frac{x_A + x_B}{2}; \frac{y_A + y_B}{2}\right)}$$
Quy tắc nhớ: “Trung bình cộng tọa độ”
Ví dụ: A(2; 3), B(6; 9) → $M\left(\frac{2+6}{2}; \frac{3+9}{2}\right) = M(4; 6)$
D. Tọa độ trọng tâm tam giác
Cho G là trọng tâm tam giác ABC:
$$\boxed{G\left(\frac{x_A + x_B + x_C}{3}; \frac{y_A + y_B + y_C}{3}\right)}$$
Quy tắc nhớ: “Trung bình cộng tọa độ ba đỉnh”
Ví dụ: A(0; 0), B(6; 0), C(0; 9) → $G\left(\frac{0+6+0}{3}; \frac{0+0+9}{3}\right) = G(2; 3)$
5. Các phép toán với tọa độ vectơ
Cho $\vec{a} = (x_1; y_1)$, $\vec{b} = (x_2; y_2)$, và $k \in \mathbb{R}$:
| Phép toán | Công thức tọa độ | Ví dụ |
|---|---|---|
| Cộng vectơ | $\vec{a} + \vec{b} = (x_1 + x_2; y_1 + y_2)$ | $(2;3)+(1;4)=(3;7)$ |
| Trừ vectơ | $\vec{a} – \vec{b} = (x_1 – x_2; y_1 – y_2)$ | $(5;6)-(2;1)=(3;5)$ |
| Nhân vectơ với số | $k\vec{a} = (kx_1; ky_1)$ | $3(2;1)=(6;3)$ |
| Tích vô hướng | $\vec{a} \cdot \vec{b} = x_1x_2 + y_1y_2$ | $(3;4)\cdot(1;2)=11$ |
| Bình phương vectơ | $\vec{a}^2 = x_1^2 + y_1^2$ | $(3;4)^2=25$ |
| Độ dài vectơ | $|\vec{a}| = \sqrt{x_1^2 + y_1^2}$ | $|(3;4)|=5$ |
Chú ý: Tất cả phép toán đều tính theo từng tọa độ (tọa độ x với x, y với y).
6. Điều kiện đặc biệt theo tọa độ
A. Hai vectơ bằng nhau
$$\boxed{\vec{a} = \vec{b} \Leftrightarrow \begin{cases} x_1 = x_2 \\ y_1 = y_2 \end{cases}}$$
B. Hai vectơ cùng phương
$$\boxed{\vec{a} \text{ // } \vec{b} \Leftrightarrow \frac{x_1}{x_2} = \frac{y_1}{y_2}}$$
Hoặc (tránh chia cho 0):
$$\boxed{x_1y_2 – x_2y_1 = 0}$$
Ví dụ: $\vec{a}=(2;3)$ và $\vec{b}=(4;6)$ → $2 \cdot 6 – 4 \cdot 3 = 0$ → Cùng phương ✓
C. Hai vectơ vuông góc
$$\boxed{\vec{a} \perp \vec{b} \Leftrightarrow x_1x_2 + y_1y_2 = 0}$$
Ví dụ: $\vec{a}=(3;4)$ và $\vec{b}=(4;-3)$ → $3 \cdot 4 + 4 \cdot (-3) = 0$ → Vuông góc ✓
D. Góc giữa hai vectơ
$$\boxed{\cos(\vec{a}, \vec{b}) = \frac{x_1x_2 + y_1y_2}{\sqrt{x_1^2 + y_1^2} \cdot \sqrt{x_2^2 + y_2^2}}}$$
Ví dụ: Tính góc giữa $\vec{a}=(1;0)$ và $\vec{b}=(1;1)$?
$$\cos(\vec{a}, \vec{b}) = \frac{1 \cdot 1 + 0 \cdot 1}{\sqrt{1} \cdot \sqrt{2}} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$$
$$\Rightarrow (\vec{a}, \vec{b}) = 45°$$
VI. ỨNG DỤNG VECTƠ TRONG HÌNH HỌC
1. Chứng minh ba điểm thẳng hàng
Phương pháp: Chứng minh $\vec{AB}$ và $\vec{AC}$ cùng phương, tức:
$$\boxed{\vec{AB} = k\vec{AC} \text{ với } k \in \mathbb{R}}$$
Ví dụ: Cho A(1; 2), B(3; 4), C(5; 6). Chứng minh A, B, C thẳng hàng?
Lời giải:
$$\vec{AB} = (3-1; 4-2) = (2; 2)$$
$$\vec{AC} = (5-1; 6-2) = (4; 4) = 2(2; 2) = 2\vec{AB}$$
Vì $\vec{AC} = 2\vec{AB}$ nên $\vec{AB}$ và $\vec{AC}$ cùng phương.
Kết luận: A, B, C thẳng hàng ✓
2. Chứng minh tứ giác là hình bình hành
Phương pháp 1: Chứng minh hai cạnh đối bằng nhau và song song:
$$\boxed{\vec{AB} = \vec{DC}}$$
Phương pháp 2: Chứng minh hai đường chéo cắt nhau tại trung điểm:
Trung điểm AC = Trung điểm BD
Ví dụ: Cho A(0; 0), B(4; 0), C(5; 3), D(1; 3). Chứng minh ABCD là hình bình hành?
Lời giải:
$$\vec{AB} = (4; 0), \quad \vec{DC} = (5-1; 3-3) = (4; 0)$$
Vì $\vec{AB} = \vec{DC}$ nên ABCD là hình bình hành ✓
3. Chứng minh hai đường thẳng vuông góc
Phương pháp: Chứng minh tích vô hướng bằng 0:
$$\boxed{\vec{AB} \cdot \vec{CD} = 0}$$
Ví dụ: Chứng minh AB ⊥ CD với A(0; 0), B(3; 4), C(0; 5), D(4; 2)?
Lời giải:
$$\vec{AB} = (3; 4), \quad \vec{CD} = (4; -3)$$
$$\vec{AB} \cdot \vec{CD} = 3 \times 4 + 4 \times (-3) = 12 – 12 = 0$$
Kết luận: AB ⊥ CD ✓
4. Tính góc trong tam giác
Phương pháp: Sử dụng công thức tích vô hướng:
$$\boxed{\cos A = \frac{\vec{AB} \cdot \vec{AC}}{AB \cdot AC}}$$
Ví dụ: Cho tam giác ABC với A(0; 0), B(3; 0), C(0; 4). Tính góc A?
Lời giải:
$$\vec{AB} = (3; 0), \quad \vec{AC} = (0; 4)$$
$$\vec{AB} \cdot \vec{AC} = 3 \times 0 + 0 \times 4 = 0$$
Vì tích vô hướng bằng 0 nên $\widehat{A} = 90°$
Kết luận: Tam giác ABC vuông tại A ✓
5. Chứng minh đẳng thức hình học
Ví dụ: Định lý trung tuyến
Cho tam giác ABC, M là trung điểm BC. Chứng minh:
$$\boxed{MA^2 + MB^2 + MC^2 = 3MG^2 + \frac{1}{4}(AB^2 + BC^2 + CA^2)}$$
(G là trọng tâm)
Chứng minh bằng vectơ:
Sử dụng các công thức:
- $\vec{MG} = \frac{1}{3}\vec{MA}$ (G chia trung tuyến theo tỉ lệ 2:1)
- $|\vec{a} + \vec{b}|^2 = |\vec{a}|^2 + 2\vec{a} \cdot \vec{b} + |\vec{b}|^2$
- $\vec{MB} + \vec{MC} = \vec{0}$ (M là trung điểm BC)
(Chi tiết chứng minh khá dài, học sinh cần thực hành)
VII. BẢNG TÓM TẮT CÔNG THỨC
A. Phép toán vectơ
| Công thức | Nội dung | Ghi chú |
|---|---|---|
| Quy tắc ba điểm | $\vec{AB} + \vec{BC} = \vec{AC}$ | Điểm cuối nối điểm đầu |
| Quy tắc hiệu | $\vec{AB} – \vec{AC} = \vec{CB}$ | Hiệu → vectơ từ cuối về đầu |
| Cùng phương | $\vec{b} = k\vec{a}$ | Tồn tại số k |
| Trung điểm M của AB | $\vec{OM} = \frac{\vec{OA} + \vec{OB}}{2}$ | O bất kỳ |
| Trọng tâm G của △ABC | $\vec{OG} = \frac{\vec{OA} + \vec{OB} + \vec{OC}}{3}$ | O bất kỳ |
| Chia đoạn | $\vec{OM} = \frac{\vec{OA} + k\vec{OB}}{1+k}$ | M chia AB theo tỉ số k |
B. Tích vô hướng
| Công thức | Nội dung | Điều kiện |
|---|---|---|
| Định nghĩa | $\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos(\vec{a}, \vec{b})$ | $\vec{a}, \vec{b} \neq \vec{0}$ |
| Bình phương | $\vec{a}^2 = |\vec{a}|^2$ | Luôn đúng |
| Độ dài | $|\vec{a}| = \sqrt{\vec{a}^2}$ | Luôn dương |
| Vuông góc | $\vec{a} \perp \vec{b} \Leftrightarrow \vec{a} \cdot \vec{b} = 0$ | Điều kiện cần và đủ |
| Góc | $\cos(\vec{a}, \vec{b}) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \cdot |\vec{b}|}$ | $\vec{a}, \vec{b} \neq \vec{0}$ |
| Hằng đẳng thức | $(\vec{a} \pm \vec{b})^2 = \vec{a}^2 \pm 2\vec{a} \cdot \vec{b} + \vec{b}^2$ | Như đại số |
C. Tọa độ vectơ
| Công thức | Nội dung | Ví dụ |
|---|---|---|
| Vectơ $\vec{AB}$ | $(x_B – x_A; y_B – y_A)$ | A(1;2), B(3;5) → (2;3) |
| Độ dài | $AB = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}$ | → $AB = \sqrt{13}$ |
| Trung điểm M | $\left(\frac{x_A+x_B}{2}; \frac{y_A+y_B}{2}\right)$ | → M(2; 3.5) |
| Trọng tâm G | $\left(\frac{x_A+x_B+x_C}{3}; \frac{y_A+y_B+y_C}{3}\right)$ | Ba đỉnh tam giác |
| Cộng | $\vec{a} + \vec{b} = (x_1+x_2; y_1+y_2)$ | (1;2)+(3;4)=(4;6) |
| Nhân số | $k\vec{a} = (kx_1; ky_1)$ | 2(3;4)=(6;8) |
| Tích vô hướng | $\vec{a} \cdot \vec{b} = x_1x_2 + y_1y_2$ | (1;2)·(3;4)=11 |
| Cùng phương | $x_1y_2 – x_2y_1 = 0$ | Không chia cho 0 |
| Vuông góc | $x_1x_2 + y_1y_2 = 0$ | Tích vô hướng = 0 |
D. Công thức đặc biệt
| Bài toán | Công thức |
|---|---|
| Ba điểm thẳng hàng | $\vec{AB} = k\vec{AC}$ |
| Hình bình hành ABCD | $\vec{AB} = \vec{DC}$ |
| Hai đường thẳng vuông góc | $\vec{AB} \cdot \vec{CD} = 0$ |
| Khoảng cách | $d(A, B) = |\vec{AB}|$ |
VIII. KẾT LUẬN
Tổng kết kiến thức
Qua bài viết này, chúng ta đã hệ thống hóa đầy đủ công thức vectơ lớp 10:
Phép toán vectơ cơ bản:
- Cộng vectơ (quy tắc hình bình hành, quy tắc ba điểm)
- Trừ vectơ (quy tắc hiệu)
- Nhân vectơ với số (độ dài và hướng)
- Điều kiện cùng phương
Quy tắc phân tích đặc biệt:
- Quy tắc trung điểm: $\vec{OM} = \frac{\vec{OA} + \vec{OB}}{2}$
- Quy tắc trọng tâm: $\vec{OG} = \frac{\vec{OA} + \vec{OB} + \vec{OC}}{3}$
- Công thức chia đoạn thẳng
Tích vô hướng:
- Định nghĩa và tính chất
- Điều kiện vuông góc
- Công thức tính góc và độ dài
- Các hằng đẳng thức vectơ
Tọa độ vectơ trong Oxy:
- Các phép toán với tọa độ
- Công thức tọa độ cơ bản (trung điểm, trọng tâm, độ dài)
- Điều kiện đặc biệt (cùng phương, vuông góc)
Ứng dụng trong hình học:
- Chứng minh thẳng hàng, song song, vuông góc
- Chứng minh tứ giác đặc biệt
- Tính góc, độ dài, diện tích

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
