Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ CHUYỂN ĐỘNG NÉM NGANG
- 1. Chuyển động ném ngang là gì?
- 2. Phân tích chuyển động ném ngang
- 3. Các đại lượng cơ bản
- II. CÁC CÔNG THỨC THÀNH PHẦN
- 1. Chuyển động theo phương ngang (Ox)
- 2. Chuyển động theo phương thẳng đứng (Oy)
- III. CÔNG THỨC CHÍNH CỦA NÉM NGANG
- 1. Thời gian rơi (thời gian bay)
- 2. Tầm xa (công thức tầm xa ném ngang)
- 3. Phương trình quỹ đạo
- 4. Vận tốc tại thời điểm t
- IV. BẢNG CÔNG THỨC TỔNG HỢP
- A. Công thức theo thời gian t
- B. Công thức đặc trưng chính
- C. Công thức vận tốc chi tiết
- D. Các công thức biến đổi hữu ích
- V. CÁC TRƯỜNG HỢP ĐẶC BIỆT
- 1. Ném ngang từ cùng độ cao (cùng h)
- 2. Ném ngang với cùng vận tốc (cùng $v_0$)
- 3. So sánh với rơi tự do
- VI. MẸO VÀ LƯU Ý
- 1. Mẹo giải nhanh – Quy trình 2 bước
- 2. Các sai lầm thường gặp
- 3. Kiểm tra kết quả
- VII. BÀI TẬP MẪU
- VIII. KẾT LUẬN
- Hai công thức cốt lõi CẦN NHỚ THUỘC
- Nguyên lý chính
- Điểm quan trọng cần nhớ
I. GIỚI THIỆU VỀ CHUYỂN ĐỘNG NÉM NGANG
1. Chuyển động ném ngang là gì?
Định nghĩa:
Chuyển động ném ngang là chuyển động của vật được ném theo phương ngang từ một độ cao h với vận tốc ban đầu $v_0$, chỉ chịu tác dụng của trọng lực (bỏ qua sức cản không khí).
Đặc điểm cơ bản:
- Vận tốc ban đầu $v_0$: Theo phương ngang (không có thành phần thẳng đứng)
- Lực tác dụng: Chỉ có trọng lực $\vec{P} = m\vec{g}$ (hướng thẳng đứng xuống)
- Gia tốc: $\vec{a} = \vec{g}$ (hướng xuống, độ lớn $g = 10$ m/s²)
- Giả thiết: Bỏ qua sức cản không khí, coi chuyển động trong chân không
Ví dụ thực tế:
- Viên bi lăn ra khỏi mép bàn
- Nước phun từ vòi ngang
- Máy bay thả hàng cứu trợ khi bay ngang
2. Phân tích chuyển động ném ngang
Nguyên lý độc lập: Chuyển động ném ngang được phân tích thành tổng hợp của hai chuyển động thành phần độc lập:
| Thành phần | Phương | Loại chuyển động | Đặc điểm |
|---|---|---|---|
| Ngang (Ox) | Phương ngang | Thẳng đều | $v_x = v_0 = const$
Không có gia tốc |
| Thẳng đứng (Oy) | Phương thẳng đứng | Rơi tự do | $v_y$ tăng dần
$a = g = 10$ m/s² |
Sơ đồ minh họa:
O ─────────→ v₀ (vận tốc ném ngang)
│
h │ ╱ (Quỹ đạo parabol)
│ ╱
│ ╱
↓ ╱
════════════════ Mặt đất
L (tầm xa)
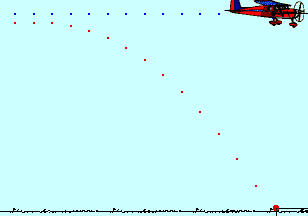
Giải thích:
- Điểm O: Vị trí ném (độ cao h)
- Chiều ngang: Vật chuyển động đều với vận tốc $v_0$
- Chiều thẳng đứng: Vật rơi tự do
- Quỹ đạo: Đường cong parabol
- Điểm chạm đất: Cách điểm ném một đoạn L (tầm xa)
3. Các đại lượng cơ bản
Đại lượng cho trước:
- $v_0$: Vận tốc ném ban đầu (m/s) – theo phương ngang
- $h$: Độ cao ném (m) – khoảng cách từ điểm ném đến mặt đất
- $g$: Gia tốc trọng trường = 10 m/s² (hoặc 9.8 m/s²)
Đại lượng cần tìm:
- $t$: Thời gian bay (thời gian rơi) (s)
- $L$: Tầm xa – khoảng cách ngang từ điểm ném đến điểm chạm đất (m)
- $x, y$: Tọa độ của vật tại thời điểm t
- $v_x, v_y$: Thành phần vận tốc theo Ox và Oy (m/s)
- $v$: Vận tốc tại thời điểm t (m/s)
Hệ tọa độ:
- Gốc O: Tại vị trí ném
- Trục Ox: Nằm ngang, chiều dương theo chiều ném
- Trục Oy: Thẳng đứng, chiều dương hướng xuống (hoặc lên tùy chọn)
II. CÁC CÔNG THỨC THÀNH PHẦN
1. Chuyển động theo phương ngang (Ox)
Đặc điểm: Chuyển động thẳng đều (không có gia tốc)
Nguyên nhân: Không có lực theo phương ngang (bỏ qua sức cản không khí)
Vận tốc theo phương Ox:
$$\boxed{v_x = v_0 = \text{const}}$$
Giải thích: Vận tốc theo phương ngang không đổi trong suốt quá trình bay.
Đặc điểm:
- Không thay đổi theo thời gian
- Bằng vận tốc ném ban đầu $v_0$
- Đây là điểm khác biệt với chuyển động rơi tự do thông thường
Tọa độ x tại thời điểm t:
$$\boxed{x = v_0 t}$$
Giải thích: Quãng đường theo phương ngang tỉ lệ thuận với thời gian.
Ứng dụng:
- Tính khoảng cách ngang vật đi được sau thời gian t
- Tính thời gian để vật đạt đến vị trí có tọa độ x cho trước
Ví dụ 1: Ném vật theo phương ngang với $v_0 = 10$ m/s. Sau 2 giây, vật bay được quãng đường ngang bao nhiêu?
Lời giải: $$x = v_0 t = 10 \times 2 = 20 \text{ m}$$
Đáp án: 20 mét
2. Chuyển động theo phương thẳng đứng (Oy)
Đặc điểm: Rơi tự do (chuyển động nhanh dần đều với gia tốc $g$)
Nguyên nhân: Chịu tác dụng của trọng lực $\vec{P} = m\vec{g}$
Vận tốc theo phương Oy:
$$\boxed{v_y = gt}$$
Giải thích: Vận tốc theo phương thẳng đứng tăng dần theo thời gian.
Lưu ý quan trọng:
- Ban đầu: $v_y(0) = 0$ (vật được ném ngang, không có thành phần vận tốc thẳng đứng ban đầu)
- Vận tốc tăng đều: Do gia tốc trọng trường $g$
- Hướng: Luôn hướng xuống dưới
Tọa độ y tại thời điểm t:
Trường hợp 1: Chọn chiều dương hướng xuống, gốc O tại vị trí ném
$$\boxed{y = \frac{1}{2}gt^2}$$
Trường hợp 2: Chọn chiều dương hướng lên, gốc tại mặt đất
$$\boxed{y = h – \frac{1}{2}gt^2}$$
Trong đó:
- $h$: độ cao ban đầu (độ cao điểm ném so với mặt đất)
- $y$: độ cao của vật tại thời điểm t
Lưu ý: Phải thống nhất cách chọn chiều dương trong suốt bài toán!
Ví dụ 2: Ném vật từ độ cao h = 20 m. Sau 1 giây, vật còn cách mặt đất bao nhiêu mét?
Lời giải:
Chọn chiều dương hướng lên, gốc tại mặt đất: $$y = h – \frac{1}{2}gt^2 = 20 – \frac{1}{2}(10)(1)^2 = 20 – 5 = 15 \text{ m}$$
Đáp án: Vật còn cách mặt đất 15 mét.
Ví dụ 3: Tính vận tốc theo phương thẳng đứng sau 2 giây?
Lời giải: $$v_y = gt = 10 \times 2 = 20 \text{ m/s}$$
Đáp án: 20 m/s (hướng xuống)
III. CÔNG THỨC CHÍNH CỦA NÉM NGANG
1. Thời gian rơi (thời gian bay)
Khi vật chạm đất: Tọa độ y = 0 (nếu đo từ mặt đất) hoặc y = h (nếu đo từ điểm ném)
Từ công thức: $h = \frac{1}{2}gt^2$
📌 Công thức thời gian rơi:
$$\boxed{t = \sqrt{\frac{2h}{g}}}$$
Đây là công thức CỰC KỲ QUAN TRỌNG!
Lưu ý đặc biệt:
✅ Thời gian rơi CHỈ phụ thuộc vào độ cao h
✅ Thời gian rơi KHÔNG phụ thuộc vào vận tốc ném $v_0$
Ý nghĩa vật lý:
- Dù ném nhanh hay chậm, từ cùng độ cao thì thời gian chạm đất là như nhau!
- Vật ném ngang và vật rơi tự do từ cùng độ cao có cùng thời gian rơi
Ví dụ 4: Ném ngang từ độ cao 20 m. Tính thời gian vật chạm đất? (g = 10 m/s²)
Lời giải: $$t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 20}{10}} = \sqrt{4} = 2 \text{ s}$$
Đáp án: 2 giây
Ví dụ 5: Từ cùng độ cao 45 m, ném một vật với v₁ = 10 m/s và một vật khác với v₂ = 20 m/s. So sánh thời gian rơi?
Lời giải:
Do cùng độ cao h = 45 m: $$t_1 = t_2 = \sqrt{\frac{2 \times 45}{10}} = \sqrt{9} = 3 \text{ s}$$
Kết luận: Thời gian rơi BẰNG NHAU = 3 giây (không phụ thuộc $v_0$)
2. Tầm xa (công thức tầm xa ném ngang)
Định nghĩa: Tầm xa L là khoảng cách theo phương ngang từ điểm ném đến điểm vật chạm đất.
Khi vật chạm đất ($t = \sqrt{\frac{2h}{g}}$), tọa độ ngang là:
$$L = v_0 t$$
Công thức tầm xa:
$$\boxed{L = v_0 t = v_0 \sqrt{\frac{2h}{g}}}$$
Hoặc viết gọn:
$$\boxed{L = v_0 \sqrt{\frac{2h}{g}}}$$
Lưu ý quan trọng:
Tầm xa phụ thuộc VÀO CẢ hai yếu tố:
- Vận tốc ném $v_0$ (tỉ lệ thuận)
- Độ cao h (tỉ lệ thuận với $\sqrt{h}$)
Muốn tăng tầm xa:
- Tăng vận tốc ném $v_0$
- Tăng độ cao ném h
Ví dụ 6: Ném vật với $v_0 = 10$ m/s từ độ cao 20 m. Tính tầm xa?
Lời giải:
Cách 1: Tính qua hai bước
- Thời gian rơi: $t = \sqrt{\frac{2 \times 20}{10}} = 2$ s
- Tầm xa: $L = v_0 t = 10 \times 2 = 20$ m
Cách 2: Dùng công thức trực tiếp $$L = v_0 \sqrt{\frac{2h}{g}} = 10 \times \sqrt{\frac{2 \times 20}{10}} = 10 \times 2 = 20 \text{ m}$$
Đáp án: Tầm xa 20 mét.
Ví dụ 7: So sánh tầm xa của hai vật ném từ cùng độ cao với $v_1 = 10$ m/s và $v_2 = 20$ m/s?
Lời giải:
Do cùng độ cao h (cùng thời gian t): $$\frac{L_1}{L_2} = \frac{v_1 t}{v_2 t} = \frac{v_1}{v_2} = \frac{10}{20} = \frac{1}{2}$$
Kết luận: $L_2 = 2L_1$ (tầm xa tỉ lệ thuận với $v_0$)
3. Phương trình quỹ đạo
Từ phương trình tọa độ:
- $x = v_0 t$ → $t = \frac{x}{v_0}$
- $y = \frac{1}{2}gt^2$
Thay $t = \frac{x}{v_0}$ vào phương trình y:
$$y = \frac{1}{2}g\left(\frac{x}{v_0}\right)^2 = \frac{g}{2v_0^2}x^2$$
Phương trình quỹ đạo (đo từ điểm ném):
$$\boxed{y = \frac{g}{2v_0^2}x^2}$$
Phương trình quỹ đạo (đo từ mặt đất):
$$\boxed{y = h – \frac{g}{2v_0^2}x^2}$$
Dạng toán học: Parabol với bề lõm hướng xuống
Đặc điểm:
- Quỹ đạo là đường cong parabol
- Bề lõm hướng xuống (do g > 0)
- Đỉnh parabol tại điểm ném (x = 0, y = h)
Ví dụ 8: Ném ngang với $v_0 = 10$ m/s từ độ cao h = 20 m. Viết phương trình quỹ đạo?
Lời giải:
Đo từ mặt đất (chiều dương hướng lên): $$y = h – \frac{g}{2v_0^2}x^2 = 20 – \frac{10}{2(10)^2}x^2 = 20 – \frac{10}{200}x^2 = 20 – \frac{x^2}{20}$$
Hoặc viết: $$y = 20 – 0.05x^2$$
Kiểm tra:
- Tại x = 0 (điểm ném): y = 20 m ✓
- Tại x = 20 m (tầm xa): y = 20 – 0.05(400) = 0 ✓ (chạm đất)
4. Vận tốc tại thời điểm t
Tại mỗi thời điểm t, vận tốc có hai thành phần:
Thành phần vận tốc:
Theo phương ngang: $$\boxed{v_x = v_0}$$
Theo phương thẳng đứng: $$\boxed{v_y = gt}$$
Độ lớn vận tốc tại thời điểm t:
$$\boxed{v = \sqrt{v_x^2 + v_y^2} = \sqrt{v_0^2 + (gt)^2}}$$
Vận tốc khi chạm đất:
Thay $t = \sqrt{\frac{2h}{g}}$ vào công thức trên:
$$v = \sqrt{v_0^2 + \left(g\sqrt{\frac{2h}{g}}\right)^2}$$
$$= \sqrt{v_0^2 + g^2 \cdot \frac{2h}{g}}$$
$$\boxed{v = \sqrt{v_0^2 + 2gh}}$$
Lưu ý:
- Vận tốc khi chạm đất luôn lớn hơn $v_0$
- Nếu $v_0 = 0$ (rơi tự do): $v = \sqrt{2gh}$
Góc nghiêng của vận tốc với phương ngang:
$$\boxed{\tan \alpha = \frac{v_y}{v_x} = \frac{gt}{v_0}}$$
Ứng dụng: Tính góc nghiêng của quỹ đạo tại một điểm bất kỳ.
Ví dụ 9: Ném ngang với $v_0 = 10$ m/s từ độ cao h = 20 m. Tính vận tốc và góc khi vật chạm đất?
Lời giải:
a) Vận tốc khi chạm đất:
$$v = \sqrt{v_0^2 + 2gh} = \sqrt{10^2 + 2(10)(20)}$$ $$= \sqrt{100 + 400} = \sqrt{500} = 10\sqrt{5} \approx 22.4 \text{ m/s}$$
b) Góc với phương ngang:
Thời gian rơi: $t = \sqrt{\frac{2 \times 20}{10}} = 2$ s
$$\tan \alpha = \frac{gt}{v_0} = \frac{10 \times 2}{10} = 2$$
$$\alpha = \arctan(2) \approx 63.4°$$
Đáp án:
- Vận tốc: ≈ 22.4 m/s
- Góc: ≈ 63.4° (so với phương ngang)
IV. BẢNG CÔNG THỨC TỔNG HỢP
A. Công thức theo thời gian t
| Đại lượng | Công thức | Ghi chú |
|---|---|---|
| Tọa độ x | $x = v_0 t$ | Chuyển động thẳng đều |
| Tọa độ y | $y = h – \frac{1}{2}gt^2$ | Đo từ mặt đất |
| Vận tốc $v_x$ | $v_x = v_0$ | Không đổi |
| Vận tốc $v_y$ | $v_y = gt$ | Tăng dần |
| Vận tốc v | $v = \sqrt{v_0^2 + (gt)^2}$ | Độ lớn vận tốc |
B. Công thức đặc trưng chính
| Đại lượng | Công thức | Phụ thuộc |
|---|---|---|
| Thời gian rơi | $t = \sqrt{\frac{2h}{g}}$ | Chỉ h (không phụ thuộc $v_0$) |
| Tầm xa | $L = v_0\sqrt{\frac{2h}{g}}$ | Cả $v_0$ và h |
| Quỹ đạo | $y = h – \frac{g}{2v_0^2}x^2$ | Parabol |
| Vận tốc chạm đất | $v = \sqrt{v_0^2 + 2gh}$ | Cả $v_0$ và h |
| Góc với ngang | $\tan \alpha = \frac{gt}{v_0}$ | t và $v_0$ |
C. Công thức vận tốc chi tiết
| Loại vận tốc | Công thức | Khi nào dùng |
|---|---|---|
| Vận tốc tại t | $v = \sqrt{v_0^2 + (gt)^2}$ | Biết thời gian t |
| Vận tốc chạm đất | $v = \sqrt{v_0^2 + 2gh}$ | Không cần biết t |
| Thành phần $v_x$ | $v_x = v_0$ | Luôn không đổi |
| Thành phần $v_y$ | $v_y = gt$ | Tại thời điểm t |
| Thành phần $v_y$ chạm đất | $v_y = \sqrt{2gh}$ | Khi chạm đất |
D. Các công thức biến đổi hữu ích
1. Tầm xa theo thời gian: $$L = v_0 t$$
2. Độ cao theo tầm xa và $v_0$: $$h = \frac{gL^2}{2v_0^2}$$
3. Vận tốc ban đầu theo tầm xa và độ cao: $$v_0 = \frac{L}{\sqrt{\frac{2h}{g}}} = L\sqrt{\frac{g}{2h}}$$
4. Thời gian theo tầm xa và $v_0$: $$t = \frac{L}{v_0}$$
V. CÁC TRƯỜNG HỢP ĐẶC BIỆT
1. Ném ngang từ cùng độ cao (cùng h)
Nếu $h_1 = h_2 = h$ nhưng $v_{01} \neq v_{02}$
Thời gian rơi: $$t_1 = t_2 = \sqrt{\frac{2h}{g}}$$
Kết luận: Thời gian rơi BẰNG NHAU (chỉ phụ thuộc h)
Tầm xa: $$\frac{L_1}{L_2} = \frac{v_{01} t}{v_{02} t} = \frac{v_{01}}{v_{02}}$$
Kết luận: Tầm xa tỉ lệ thuận với vận tốc ném $v_0$
Ví dụ 10: Hai vật ném từ cùng độ cao 45 m với $v_1 = 15$ m/s và $v_2 = 30$ m/s. So sánh t và L?
Lời giải:
Thời gian: $$t_1 = t_2 = \sqrt{\frac{2 \times 45}{10}} = 3 \text{ s}$$ (BẰNG NHAU)
Tầm xa:
- $L_1 = 15 \times 3 = 45$ m
- $L_2 = 30 \times 3 = 90$ m
- $\frac{L_2}{L_1} = \frac{30}{15} = 2$ → $L_2 = 2L_1$
2. Ném ngang với cùng vận tốc (cùng $v_0$)
Nếu $v_{01} = v_{02} = v_0$ nhưng $h_1 \neq h_2$
Thời gian rơi: $$\frac{t_1}{t_2} = \sqrt{\frac{h_1}{h_2}}$$
Tầm xa: $$\frac{L_1}{L_2} = \frac{v_0 t_1}{v_0 t_2} = \frac{t_1}{t_2} = \sqrt{\frac{h_1}{h_2}}$$
Kết luận:
- Thời gian và tầm xa đều tỉ lệ với $\sqrt{h}$
- Độ cao tăng gấp 4 lần → thời gian và tầm xa tăng gấp 2 lần
Ví dụ 11: Cùng $v_0 = 20$ m/s, ném từ h₁ = 20 m và h₂ = 80 m. So sánh?
Lời giải:
$$\frac{h_2}{h_1} = \frac{80}{20} = 4$$
$$\frac{t_2}{t_1} = \sqrt{4} = 2$$ → $t_2 = 2t_1$
$$\frac{L_2}{L_1} = \sqrt{4} = 2$$ → $L_2 = 2L_1$
3. So sánh với rơi tự do
Vật ném ngang và vật rơi tự do từ cùng độ cao h:
| Đại lượng | Ném ngang | Rơi tự do | So sánh |
|---|---|---|---|
| Thời gian chạm đất | $t = \sqrt{\frac{2h}{g}}$ | $t = \sqrt{\frac{2h}{g}}$ | BẰNG NHAU |
| $v_y$ chạm đất | $v_y = \sqrt{2gh}$ | $v_y = \sqrt{2gh}$ | BẰNG NHAU |
| Tốc độ chạm đất | $v = \sqrt{v_0^2 + 2gh}$ | $v = \sqrt{2gh}$ | Ném ngang LỚN HƠN |
| Tầm xa | $L = v_0\sqrt{\frac{2h}{g}}$ | $L = 0$ | Ném ngang LỚN HƠN |
Kết luận quan trọng:
- Thời gian rơi như nhau (không phụ thuộc $v_0$)
- Vận tốc theo phương thẳng đứng như nhau
- Tốc độ tổng hợp: ném ngang lớn hơn (có thêm $v_x = v_0$)
VI. MẸO VÀ LƯU Ý
1. Mẹo giải nhanh – Quy trình 2 bước
Bước 1: LUÔN tính thời gian rơi trước
$$t = \sqrt{\frac{2h}{g}}$$
Lý do: Thời gian rơi là đại lượng cơ bản, chỉ phụ thuộc h.
Bước 2: Từ t → tính các đại lượng khác
- Tầm xa: $L = v_0 t$
- Tọa độ x: $x = v_0 t$
- Tọa độ y: $y = h – \frac{1}{2}gt^2$
- Vận tốc $v_y$: $v_y = gt$
- Vận tốc tổng hợp: $v = \sqrt{v_0^2 + v_y^2}$
Công thức nhanh tầm xa (không cần tính t):
$$L = v_0\sqrt{\frac{2h}{g}}$$
Dùng khi đề bài không hỏi thời gian.
2. Các sai lầm thường gặp
❌ Sai lầm 1: Nghĩ thời gian rơi phụ thuộc vào $v_0$
SAI: “Ném nhanh hơn thì chạm đất nhanh hơn”
ĐÚNG: Thời gian rơi CHỈ phụ thuộc độ cao h, KHÔNG phụ thuộc $v_0$
Giải thích: Vận tốc ngang không ảnh hưởng đến chuyển động thẳng đứng (nguyên lý độc lập các chuyển động)
❌ Sai lầm 2: Dùng công thức ném xiên cho ném ngang
Ném ngang là trường hợp đặc biệt của ném xiên với góc ném 0°.
KHÔNG dùng:
- Công thức tầm xa ném xiên: $L = \frac{v_0^2 \sin 2\alpha}{g}$
- Công thức độ cao cực đại ném xiên
❌ Sai lầm 3: Quên $\frac{1}{2}$ trong công thức
SAI: $y = gt^2$ (thiếu $\frac{1}{2}$)
ĐÚNG: $y = \frac{1}{2}gt^2$
❌ Sai lầm 4: Nhầm lẫn chiều dương của trục Oy
Phải thống nhất chiều dương trong suốt bài toán:
- Nếu chọn hướng xuống làm dương → $y = \frac{1}{2}gt^2$
- Nếu chọn hướng lên làm dương → $y = h – \frac{1}{2}gt^2$
❌ Sai lầm 5: Nhầm vận tốc ban đầu có thành phần thẳng đứng
SAI: Cho $v_0$ có cả thành phần ngang và đứng
ĐÚNG: Ném NGANG → $v_0$ chỉ theo phương ngang, không có thành phần thẳng đứng
Nếu có thành phần thẳng đứng → Đó là ném xiên, không phải ném ngang!
3. Kiểm tra kết quả
Sau khi giải xong, luôn kiểm tra:
Thời gian luôn dương: $t > 0$
Tầm xa luôn dương: $L > 0$
Vận tốc chạm đất lớn hơn $v_0$: $v > v_0$
Khi $v_0 = 0$ (rơi tự do):
- Tầm xa: $L = 0$ ✓
- Vận tốc chạm đất: $v = \sqrt{2gh}$ ✓
Đơn vị phải khớp:
- Thời gian: giây (s)
- Khoảng cách: mét (m)
- Vận tốc: m/s
VII. BÀI TẬP MẪU
Bài 1: Tính thời gian và tầm xa cơ bản
Đề bài: Ném ngang một vật với vận tốc $v_0 = 20$ m/s từ độ cao h = 45 m. Lấy $g = 10$ m/s². Tính: a) Thời gian vật rơi
b) Tầm xa
Lời giải:
a) Thời gian rơi: $$t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 45}{10}} = \sqrt{9} = 3 \text{ s}$$
b) Tầm xa: $$L = v_0 t = 20 \times 3 = 60 \text{ m}$$
Đáp án: a) 3 giây, b) 60 mét
Bài 2: Tính vận tốc khi chạm đất
Đề bài: (Tiếp bài 1) Tính: a) Các thành phần vận tốc khi chạm đất
b) Độ lớn vận tốc khi chạm đất
c) Góc nghiêng của vận tốc với phương ngang
Lời giải:
a) Thành phần vận tốc:
- Theo Ox: $v_x = v_0 = 20$ m/s
- Theo Oy: $v_y = gt = 10 \times 3 = 30$ m/s
b) Độ lớn vận tốc: $$v = \sqrt{v_x^2 + v_y^2} = \sqrt{20^2 + 30^2}$$ $$= \sqrt{400 + 900} = \sqrt{1300} = 10\sqrt{13} \approx 36.1 \text{ m/s}$$
Hoặc dùng công thức trực tiếp: $$v = \sqrt{v_0^2 + 2gh} = \sqrt{20^2 + 2(10)(45)}$$ $$= \sqrt{400 + 900} = \sqrt{1300} \approx 36.1 \text{ m/s}$$
c) Góc với phương ngang: $$\tan \alpha = \frac{v_y}{v_x} = \frac{30}{20} = 1.5$$ $$\alpha = \arctan(1.5) \approx 56.3°$$
Đáp án:
- a) $v_x = 20$ m/s, $v_y = 30$ m/s
- b) $v \approx 36.1$ m/s
- c) $\alpha \approx 56.3°$
Bài 3: Tìm vận tốc ban đầu
Đề bài: Ném ngang một vật từ độ cao 20 m. Vật rơi chạm đất cách chân tháp 40 m (theo phương ngang). Tính vận tốc ném ban đầu? ($g = 10$ m/s²)
Lời giải:
Bước 1: Tính thời gian rơi $$t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 20}{10}} = 2 \text{ s}$$
Bước 2: Tính vận tốc ban đầu Từ $L = v_0 t$: $$v_0 = \frac{L}{t} = \frac{40}{2} = 20 \text{ m/s}$$
Đáp án: Vận tốc ban đầu 20 m/s
Bài 4: Viết phương trình quỹ đạo
Đề bài: Ném ngang vật với $v_0 = 10$ m/s từ độ cao h = 5 m. Viết phương trình quỹ đạo (đo từ mặt đất, chiều dương hướng lên)?
Lời giải:
Phương trình quỹ đạo: $$y = h – \frac{g}{2v_0^2}x^2$$
Thay số: $$y = 5 – \frac{10}{2(10)^2}x^2 = 5 – \frac{10}{200}x^2 = 5 – \frac{x^2}{20}$$
Hoặc: $$y = 5 – 0.05x^2$$
Kiểm tra:
- Tại x = 0: y = 5 m ✓ (đúng độ cao ban đầu)
- Quỹ đạo là parabol bề lõm hướng xuống ✓
Đáp án: $y = 5 – \frac{x^2}{20}$ (m)
Bài 5: Tọa độ tại thời điểm cho trước
Đề bài: Ném ngang vật với $v_0 = 15$ m/s từ độ cao 80 m. Tìm tọa độ của vật sau 2 giây (đo từ mặt đất, chiều dương hướng lên)?
Lời giải:
Tọa độ x: $$x = v_0 t = 15 \times 2 = 30 \text{ m}$$
Tọa độ y: $$y = h – \frac{1}{2}gt^2 = 80 – \frac{1}{2}(10)(2)^2$$ $$= 80 – 20 = 60 \text{ m}$$
Đáp án: Vật ở vị trí (30 m; 60 m)
Giải thích: Vật đã bay ngang 30 m và còn cách mặt đất 60 m.
Bài 6: So sánh hai vật
Đề bài: Hai vật được ném ngang từ cùng độ cao h = 20 m với vận tốc $v_1 = 10$ m/s và $v_2 = 20$ m/s. So sánh: a) Thời gian rơi
b) Tầm xa
c) Vận tốc khi chạm đất
Lời giải:
a) Thời gian rơi:
Do cùng độ cao: $$t_1 = t_2 = \sqrt{\frac{2 \times 20}{10}} = 2 \text{ s}$$
Kết luận: Thời gian BẰNG NHAU = 2 s
b) Tầm xa:
- $L_1 = v_1 t = 10 \times 2 = 20$ m
- $L_2 = v_2 t = 20 \times 2 = 40$ m
- $\frac{L_2}{L_1} = \frac{40}{20} = 2$
Kết luận: $L_2 = 2L_1$ (tầm xa tỉ lệ với $v_0$)
c) Vận tốc chạm đất:
- $v_1 = \sqrt{10^2 + 2(10)(20)} = \sqrt{500} \approx 22.4$ m/s
- $v_2 = \sqrt{20^2 + 2(10)(20)} = \sqrt{800} \approx 28.3$ m/s
Kết luận: Vật 2 có vận tốc lớn hơn
Bài 7: Tính độ cao từ tầm xa
Đề bài: Ném ngang vật với $v_0 = 30$ m/s, vật rơi cách điểm ném 90 m (theo phương ngang). Tính độ cao ném? ($g = 10$ m/s²)
Lời giải:
Từ $L = v_0 t$: $$t = \frac{L}{v_0} = \frac{90}{30} = 3 \text{ s}$$
Từ $t = \sqrt{\frac{2h}{g}}$: $$t^2 = \frac{2h}{g}$$ $$h = \frac{gt^2}{2} = \frac{10 \times 3^2}{2} = \frac{90}{2} = 45 \text{ m}$$
Đáp án: Độ cao 45 mét
VIII. KẾT LUẬN
Bài viết đã trình bày đầy đủ và chi tiết các công thức chuyển động ném ngang:
Thời gian rơi (công thức quan trọng nhất số 1): $$t = \sqrt{\frac{2h}{g}}$$
Đặc điểm: CHỈ phụ thuộc h, KHÔNG phụ thuộc $v_0$
Tầm xa (công thức quan trọng nhất số 2): $$L = v_0\sqrt{\frac{2h}{g}}$$
Đặc điểm: Phụ thuộc CẢ $v_0$ và h
Phương trình quỹ đạo: $$y = h – \frac{g}{2v_0^2}x^2$$
Dạng: Parabol bề lõm hướng xuống
Vận tốc khi chạm đất: $$v = \sqrt{v_0^2 + 2gh}$$
Đặc điểm: Luôn lớn hơn $v_0$
Tọa độ tại thời điểm t:
- $x = v_0 t$ (chuyển động thẳng đều)
- $y = h – \frac{1}{2}gt^2$ (rơi tự do)
Hai công thức cốt lõi CẦN NHỚ THUỘC
$$\boxed{t = \sqrt{\frac{2h}{g}}}$$
$$\boxed{L = v_0 t}$$
Từ hai công thức này có thể suy ra mọi công thức khác!
Nguyên lý chính
Ném ngang = Tổng hợp 2 chuyển động độc lập:
$$\text{Ném ngang} = \begin{cases} \text{Thẳng đều (Ox): } v_x = v_0 = const \\ \text{Rơi tự do (Oy): } v_y = gt, \, y = \frac{1}{2}gt^2 \end{cases}$$
Điểm quan trọng cần nhớ
Thời gian rơi KHÔNG phụ thuộc vận tốc ném
- Ném nhanh hay chậm, thời gian rơi như nhau (nếu cùng độ cao)
Quỹ đạo là đường parabol
- Không phải đường thẳng, không phải đường tròn
Luôn tính thời gian rơi trước tiên
- Đây là bước đầu tiên trong mọi bài toán ném ngang
Phân tích thành 2 chuyển động độc lập
- Chuyển động ngang không ảnh hưởng chuyển động thẳng đứng và ngược lại

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
