Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ CHUYỂN ĐỘNG NÉM XIÊN
- 1. Chuyển động ném xiên là gì?
- 2. Phân tích chuyển động
- 3. Các đại lượng cơ bản
- II. PHÂN TÍCH VẬN TỐC BAN ĐẦU
- 1. Thành phần vận tốc ban đầu
- 2. Vận tốc tại thời điểm t
- III. CÁC CÔNG THỨC CHÍNH CỦA NÉM XIÊN
- 1. Thời gian bay (thời gian chuyển động)
- 2. Độ cao cực đại (công thức độ cao cực đại)
- 3. Tầm xa (công thức tầm xa ném xiên)
- 4. Góc ném để tầm xa cực đại
- 5. Phương trình quỹ đạo
- IV. BẢNG CÔNG THỨC TỔNG HỢP
- A. Công thức cốt lõi
- B. Công thức thành phần
- C. Công thức đặc biệt
- D. Mối quan hệ đặc biệt
- V. SO SÁNH CÁC GÓC NÉM
- 1. Ảnh hưởng của góc ném
- 2. Hai góc cho cùng tầm xa
- 3. Bảng giá trị tham khảo
- VI. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Kiểm tra nhanh kết quả
- VII. BÀI TẬP MẪU
- VIII. KẾT LUẬN
- Ba công thức QUAN TRỌNG NHẤT
- Điểm đặc biệt cần nhớ
I. GIỚI THIỆU VỀ CHUYỂN ĐỘNG NÉM XIÊN
1. Chuyển động ném xiên là gì?
Định nghĩa: Chuyển động ném xiên là chuyển động của vật được ném với vận tốc ban đầu $v_0$ hợp với phương ngang một góc $\alpha$ (gọi là góc ném), chỉ chịu tác dụng của trọng lực.
Đặc điểm:
- Vận tốc ban đầu: Vật được ném với vận tốc $v_0$ xiên góc $\alpha$ so với phương ngang
- Lực tác dụng: Chỉ có trọng lực hướng thẳng đứng xuống dưới
- Bỏ qua: Sức cản không khí, ma sát
- Quỹ đạo: Đường parabol
Ví dụ thực tế:
- Ném lao trong thể thao
- Sút bóng trong bóng đá
- Ném đá, bắn đại bác
- Phun nước từ vòi
2. Phân tích chuyển động
Nguyên lý quan trọng: Chuyển động ném xiên được phân tích thành tổng hợp của hai chuyển động độc lập:
| Thành phần | Phương | Loại chuyển động | Đặc điểm |
|---|---|---|---|
| Ngang (Ox) | Phương ngang | Thẳng đều | $v_x = v_0\cos\alpha = \text{const}$ |
| Thẳng đứng (Oy) | Phương thẳng đứng | Ném lên thẳng đứng | $v_y$ giảm → 0 → tăng |
Sơ đồ minh họa:
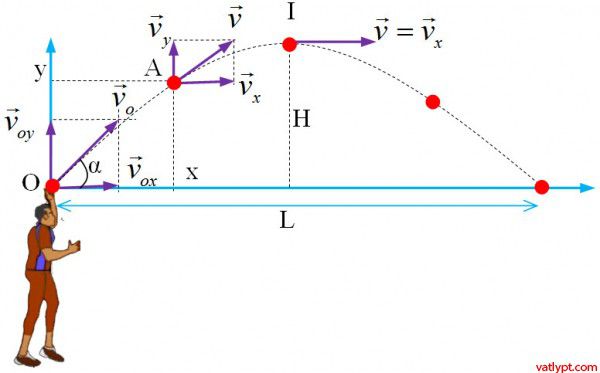
Giải thích:
- Theo phương ngang (Ox): Không có lực tác dụng → chuyển động thẳng đều với vận tốc không đổi $v_x = v_0\cos\alpha$
- Theo phương thẳng đứng (Oy): Chịu tác dụng trọng lực → chuyển động chậm dần đều (đi lên) rồi nhanh dần đều (đi xuống)
3. Các đại lượng cơ bản
Các thông số đầu vào:
- $v_0$: Vận tốc ném ban đầu (m/s)
- $\alpha$: Góc ném – góc hợp bởi $\vec{v_0}$ và phương ngang (độ hoặc radian)
- $g = 10$ m/s² (hoặc 9.8 m/s²): Gia tốc trọng trường
Các đại lượng cần tìm:
- $L$: Tầm xa – khoảng cách theo phương ngang (m)
- $h_{max}$: Độ cao cực đại – độ cao lớn nhất vật đạt được (m)
- $t$: Thời gian bay – thời gian từ lúc ném đến khi chạm đất (s)
- $x, y$: Tọa độ vật tại thời điểm bất kỳ (m)
II. PHÂN TÍCH VẬN TỐC BAN ĐẦU
1. Thành phần vận tốc ban đầu
Vận tốc ban đầu $\vec{v_0}$ được phân tích thành hai thành phần vuông góc:
Thành phần theo phương ngang (Ox): $$\boxed{v_{0x} = v_0 \cos\alpha}$$
Thành phần theo phương thẳng đứng (Oy): $$\boxed{v_{0y} = v_0 \sin\alpha}$$
Sơ đồ phân tích vectơ:
v₀
╱│
╱ │ v₀y = v₀sinα
╱ │
╱ α │
╱────┘
v₀x = v₀cosα
Quan hệ: $$v_0^2 = v_{0x}^2 + v_{0y}^2$$ $$\tan\alpha = \frac{v_{0y}}{v_{0x}}$$
Ví dụ 1: Ném vật với $v_0 = 20$ m/s, góc $\alpha = 30°$. Tính các thành phần vận tốc.
Lời giải:
Thành phần ngang: $$v_{0x} = v_0\cos\alpha = 20\cos 30° = 20 \times \frac{\sqrt{3}}{2} = 10\sqrt{3} \approx 17.32 \text{ m/s}$$
Thành phần thẳng đứng: $$v_{0y} = v_0\sin\alpha = 20\sin 30° = 20 \times 0.5 = 10 \text{ m/s}$$
Kiểm tra: $$v_0 = \sqrt{v_{0x}^2 + v_{0y}^2} = \sqrt{(10\sqrt{3})^2 + 10^2} = \sqrt{300 + 100} = 20 \text{ m/s}$$ ✓
2. Vận tốc tại thời điểm t
Thành phần ngang: (không đổi vì không có lực theo phương ngang) $$\boxed{v_x(t) = v_0\cos\alpha}$$
Thành phần thẳng đứng: (biến đổi do trọng lực) $$\boxed{v_y(t) = v_0\sin\alpha – gt}$$
Độ lớn vận tốc tại thời điểm t: $$v(t) = \sqrt{v_x^2 + v_y^2}$$
Lưu ý về dấu của $v_y$:
- Khi vật đi lên: $v_y > 0$ (hướng lên)
- Tại đỉnh quỹ đạo: $v_y = 0$
- Khi vật đi xuống: $v_y < 0$ (hướng xuống)
Tại thời điểm chạm đất:
- $v_x$ = không đổi
- $v_y$ = $-v_{0y}$ (bằng về độ lớn, ngược chiều)
- $v = v_0$ (độ lớn vận tốc khi chạm đất bằng vận tốc ban đầu)
III. CÁC CÔNG THỨC CHÍNH CỦA NÉM XIÊN
1. Thời gian bay (thời gian chuyển động)
Công thức thời gian bay:
$$\boxed{t = \frac{2v_0\sin\alpha}{g}}$$
Chứng minh:
Xét chuyển động theo phương Oy: $$y = v_{0y}t – \frac{1}{2}gt^2 = v_0\sin\alpha \cdot t – \frac{1}{2}gt^2$$
Khi chạm đất: $y = 0$ $$v_0\sin\alpha \cdot t – \frac{1}{2}gt^2 = 0$$ $$t(v_0\sin\alpha – \frac{1}{2}gt) = 0$$
Nghiệm $t = 0$ (lúc ném), nghiệm còn lại: $$t = \frac{2v_0\sin\alpha}{g}$$
Giải thích vật lý:
- Thời gian lên = thời gian xuống
- Thời gian lên đến đỉnh: $t_{lên} = \frac{v_0\sin\alpha}{g}$
- Tổng thời gian: $t = 2t_{lên} = \frac{2v_0\sin\alpha}{g}$
Ví dụ 2: Ném vật với $v_0 = 20$ m/s, góc $\alpha = 30°$. Tính thời gian bay.
Lời giải: $$t = \frac{2v_0\sin\alpha}{g} = \frac{2 \times 20 \times \sin 30°}{10} = \frac{2 \times 20 \times 0.5}{10} = \frac{20}{10} = 2 \text{ giây}$$
Đáp án: Thời gian bay là 2 giây.
2. Độ cao cực đại (công thức độ cao cực đại)
Định nghĩa: Độ cao cực đại $h_{max}$ là độ cao lớn nhất mà vật đạt được trong quá trình bay.
Công thức độ cao cực đại:
$$\boxed{h_{max} = \frac{v_0^2\sin^2\alpha}{2g}}$$
Chứng minh:
Cách 1: Sử dụng công thức độc lập thời gian
Tại đỉnh: $v_y = 0$, $v_{0y} = v_0\sin\alpha$
Áp dụng: $v_y^2 – v_{0y}^2 = -2gh_{max}$ $$0 – (v_0\sin\alpha)^2 = -2gh_{max}$$ $$h_{max} = \frac{v_0^2\sin^2\alpha}{2g}$$
Cách 2: Từ phương trình chuyển động
Tại đỉnh: $t = \frac{t_{bay}}{2} = \frac{v_0\sin\alpha}{g}$
$$h_{max} = v_0\sin\alpha \cdot t – \frac{1}{2}gt^2$$ $$= v_0\sin\alpha \cdot \frac{v_0\sin\alpha}{g} – \frac{1}{2}g\left(\frac{v_0\sin\alpha}{g}\right)^2$$ $$= \frac{v_0^2\sin^2\alpha}{g} – \frac{v_0^2\sin^2\alpha}{2g} = \frac{v_0^2\sin^2\alpha}{2g}$$
Thời gian đạt độ cao cực đại: $$\boxed{t_{h_{max}} = \frac{v_0\sin\alpha}{g} = \frac{t}{2}}$$
Ví dụ 3: Ném vật với $v_0 = 20$ m/s, góc $\alpha = 30°$. Tính độ cao cực đại và thời gian đạt được.
Lời giải:
Độ cao cực đại: $$h_{max} = \frac{v_0^2\sin^2\alpha}{2g} = \frac{20^2 \times (\sin 30°)^2}{2 \times 10}$$ $$= \frac{400 \times (0.5)^2}{20} = \frac{400 \times 0.25}{20} = \frac{100}{20} = 5 \text{ m}$$
Thời gian đạt $h_{max}$: $$t_{h_{max}} = \frac{v_0\sin\alpha}{g} = \frac{20 \times 0.5}{10} = 1 \text{ giây}$$
Đáp án:
- Độ cao cực đại: 5 m
- Thời gian đạt được: 1 giây (bằng nửa thời gian bay)
3. Tầm xa (công thức tầm xa ném xiên)
Định nghĩa: Tầm xa $L$ là khoảng cách theo phương ngang từ điểm ném đến điểm vật chạm đất.
Công thức tầm xa:
$$\boxed{L = \frac{v_0^2\sin 2\alpha}{g}}$$
Dạng khác: $$L = \frac{2v_0^2\sin\alpha\cos\alpha}{g}$$
Chứng minh:
Tầm xa = vận tốc ngang × thời gian bay $$L = v_x \times t = v_0\cos\alpha \times \frac{2v_0\sin\alpha}{g}$$ $$= \frac{2v_0^2\sin\alpha\cos\alpha}{g}$$
Sử dụng công thức lượng giác: $\sin 2\alpha = 2\sin\alpha\cos\alpha$ $$L = \frac{v_0^2\sin 2\alpha}{g}$$
Ví dụ 4: Ném vật với $v_0 = 20$ m/s, góc $\alpha = 30°$. Tính tầm xa.
Lời giải: $$L = \frac{v_0^2\sin 2\alpha}{g} = \frac{20^2 \times \sin(2 \times 30°)}{10}$$ $$= \frac{400 \times \sin 60°}{10} = \frac{400 \times \frac{\sqrt{3}}{2}}{10}$$ $$= \frac{200\sqrt{3}}{10} = 20\sqrt{3} \approx 34.64 \text{ m}$$
Đáp án: Tầm xa khoảng 34.64 m.
4. Góc ném để tầm xa cực đại
Phân tích: Từ công thức $L = \frac{v_0^2\sin 2\alpha}{g}$
Tầm xa lớn nhất khi $\sin 2\alpha$ đạt giá trị lớn nhất.
Vì $\sin 2\alpha \leq 1$, giá trị lớn nhất là 1 khi: $$\sin 2\alpha = 1 \Rightarrow 2\alpha = 90° \Rightarrow \alpha = 45°$$
Góc ném tối ưu: $$\boxed{\alpha = 45°}$$
Tầm xa cực đại: $$\boxed{L_{max} = \frac{v_0^2}{g}} \quad \text{(khi } \alpha = 45°\text{)}$$
Lưu ý quan trọng:
Hai góc bù nhau cho cùng tầm xa:
Nếu $\alpha_1 + \alpha_2 = 90°$ thì $L(\alpha_1) = L(\alpha_2)$
Chứng minh: $$\sin 2\alpha_1 = \sin(180° – 2\alpha_2) = \sin 2\alpha_2$$
Ví dụ:
- $\alpha = 30°$ và $\alpha = 60°$ → cùng tầm xa
- $\alpha = 20°$ và $\alpha = 70°$ → cùng tầm xa
- $\alpha = 40°$ và $\alpha = 50°$ → cùng tầm xa
Nhưng khác về độ cao và thời gian:
- Góc nhỏ ($< 45°$): bay thấp, nhanh
- Góc lớn ($> 45°$): bay cao, lâu
Ví dụ 5: Với $v_0 = 30$ m/s, tính tầm xa cực đại.
Lời giải:
Góc ném: $\alpha = 45°$
Tầm xa cực đại: $$L_{max} = \frac{v_0^2}{g} = \frac{30^2}{10} = \frac{900}{10} = 90 \text{ m}$$
Đáp án: 90 m (khi ném với góc 45°)
5. Phương trình quỹ đạo
Phương trình tham số:
- Theo Ox: $x = v_0\cos\alpha \cdot t$
- Theo Oy: $y = v_0\sin\alpha \cdot t – \frac{1}{2}gt^2$
Khử t: Từ phương trình thứ nhất: $t = \frac{x}{v_0\cos\alpha}$
Thay vào phương trình thứ hai:
Phương trình quỹ đạo:
$$\boxed{y = x\tan\alpha – \frac{g}{2v_0^2\cos^2\alpha}x^2}$$
Dạng khác: $$y = x\tan\alpha – \frac{gx^2}{2v_0^2}(1 + \tan^2\alpha)$$
Dạng toán học: Đây là phương trình parabol có dạng $y = ax + bx^2$ với $a > 0$, $b < 0$.
Đặc điểm:
- Đỉnh parabol tại $x = \frac{L}{2}$, $y = h_{max}$
- Cắt trục Ox tại $x = 0$ (điểm ném) và $x = L$ (điểm chạm đất)
IV. BẢNG CÔNG THỨC TỔNG HỢP
A. Công thức cốt lõi
| Đại lượng | Công thức | Ghi chú |
|---|---|---|
| Thời gian bay | $t = \frac{2v_0\sin\alpha}{g}$ | Từ ném đến chạm đất |
| Độ cao cực đại | $h_{max} = \frac{v_0^2\sin^2\alpha}{2g}$ | Chú ý $\sin^2\alpha$ |
| Tầm xa | $L = \frac{v_0^2\sin 2\alpha}{g}$ | Chú ý $\sin 2\alpha$ |
| Tầm xa cực đại | $L_{max} = \frac{v_0^2}{g}$ | Khi $\alpha = 45°$ |
B. Công thức thành phần
| Đại lượng | Phương ngang (Ox) | Phương thẳng đứng (Oy) |
|---|---|---|
| Vận tốc ban đầu | $v_{0x} = v_0\cos\alpha$ | $v_{0y} = v_0\sin\alpha$ |
| Vận tốc tại t | $v_x = v_0\cos\alpha$ | $v_y = v_0\sin\alpha – gt$ |
| Tọa độ tại t | $x = v_0\cos\alpha \cdot t$ | $y = v_0\sin\alpha \cdot t – \frac{1}{2}gt^2$ |
| Gia tốc | $a_x = 0$ | $a_y = -g$ |
C. Công thức đặc biệt
| Đại lượng | Công thức | Điều kiện |
|---|---|---|
| Thời gian lên đỉnh | $t_{lên} = \frac{v_0\sin\alpha}{g}$ | $= \frac{t}{2}$ |
| Vận tốc tại đỉnh | $v_{đỉnh} = v_0\cos\alpha$ | Chỉ còn thành phần ngang |
| Vận tốc chạm đất | $v = v_0$ | Độ lớn bằng ban đầu |
| Quỹ đạo parabol | $y = x\tan\alpha – \frac{gx^2}{2v_0^2\cos^2\alpha}$ | Phương trình y(x) |
| Góc tối ưu | $\alpha = 45°$ | Cho $L_{max}$ |
D. Mối quan hệ đặc biệt
Liên hệ giữa $h_{max}$ và $L$: $$\frac{h_{max}}{L} = \frac{\tan\alpha}{4}$$
Với góc 45°: $$L = 4h_{max}$$
Hai góc bù nhau: $$L(\alpha) = L(90° – \alpha)$$
Ví dụ: $L(30°) = L(60°)$, $L(20°) = L(70°)$
V. SO SÁNH CÁC GÓC NÉM
1. Ảnh hưởng của góc ném
| Góc $\alpha$ | Độ cao $h_{max}$ | Tầm xa $L$ | Thời gian $t$ |
|---|---|---|---|
| $0°$ (ngang) | $0$ (không bay lên) | $0$ | $0$ |
| $30°$ | Thấp | Trung bình | Ngắn |
| $45°$ | Trung bình | CỰC ĐẠI | Trung bình |
| $60°$ | Cao | Trung bình | Dài |
| $90°$ (thẳng đứng) | CỰC ĐẠI | $0$ (không bay xa) | Dài nhất |
Nhận xét:
- Góc càng lớn → bay càng cao, càng lâu
- Góc 45° → tầm xa lớn nhất
- Góc 90° → bay cao nhất nhưng không xa
2. Hai góc cho cùng tầm xa
Quy luật: Hai góc bù nhau $(90° – \alpha)$ và $\alpha$ cho cùng tầm xa: $$L(\alpha) = L(90° – \alpha)$$
Ví dụ cụ thể:
- $L(30°) = L(60°)$
- $L(20°) = L(70°)$
- $L(10°) = L(80°)$
- $L(45°) = L(45°)$ (trường hợp đặc biệt)
Nhưng khác về các yếu tố khác:
| So sánh | Góc nhỏ ($< 45°$) | Góc lớn ($> 45°$) |
|---|---|---|
| Độ cao | Thấp hơn | Cao hơn |
| Thời gian | Ngắn hơn | Dài hơn |
| Quỹ đạo | Dẹt hơn | Vút cao hơn |
3. Bảng giá trị tham khảo
Với $v_0 = 20$ m/s, $g = 10$ m/s²:
| Góc $\alpha$ | $h_{max}$ (m) | $L$ (m) | $t$ (s) |
|---|---|---|---|
| $0°$ | $0$ | $0$ | $0$ |
| $30°$ | $5$ | $34.64$ | $2$ |
| $45°$ | $10$ | $40$ | $2.83$ |
| $60°$ | $15$ | $34.64$ | $3.46$ |
| $90°$ | $20$ | $0$ | $4$ |
Nhận xét:
- $L(30°) = L(60°) \approx 34.64$ m ✓
- $L(45°) = 40$ m là lớn nhất ✓
- $h_{max}(60°) > h_{max}(45°) > h_{max}(30°)$ ✓
VI. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Mẹo 1: Phân biệt $\sin\alpha$ và $\sin 2\alpha$
Tầm xa dùng $\sin 2\alpha$: $L = \frac{v_0^2\sin 2\alpha}{g}$
Độ cao dùng $\sin^2\alpha$: $h_{max} = \frac{v_0^2\sin^2\alpha}{2g}$
Cách nhớ: “Tầm xa cần 2 chiều (ngang + đứng) → $\sin 2\alpha$”
Mẹo 2: Góc 45° là “góc vàng”
- Ném với góc 45° → Tầm xa cực đại
- $L_{max} = \frac{v_0^2}{g}$ (công thức đơn giản nhất)
- Tại góc này: $L = 4h_{max}$
Mẹo 3: Liên hệ nhanh
Từ tầm xa và độ cao: $$\frac{L}{h_{max}} = \frac{4}{\tan\alpha}$$
Ví dụ: Nếu biết $L$ và $h_{max}$, có thể tính ngay $\alpha$
Mẹo 4: Nhớ hệ số
- Thời gian bay: Có hệ số 2 → $t = \frac{2v_0\sin\alpha}{g}$
- Độ cao: Có hệ số $\frac{1}{2}$ → $h_{max} = \frac{v_0^2\sin^2\alpha}{2g}$
- Tầm xa cực đại: Không có hệ số đặc biệt → $L_{max} = \frac{v_0^2}{g}$
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm $\sin\alpha$ và $\sin 2\alpha$
Sai: $L = \frac{v_0^2\sin\alpha}{g}$ ❌
Đúng: $L = \frac{v_0^2\sin 2\alpha}{g}$ ✓
Hậu quả: Kết quả sai hoàn toàn, thiếu hệ số 2
❌ SAI LẦM 2: Quên bình phương
Sai: $h_{max} = \frac{v_0^2\sin\alpha}{2g}$ ❌
Đúng: $h_{max} = \frac{v_0^2\sin^2\alpha}{2g}$ ✓
Chú ý: Phải có $\sin^2\alpha$
❌ SAI LẦM 3: Nghĩ góc 90° cho tầm xa lớn nhất
Sai: Góc 90° cho tầm xa lớn nhất ❌
Đúng: Góc 45° cho tầm xa lớn nhất ✓
Giải thích: Góc 90° ném thẳng đứng → tầm xa = 0
❌ SAI LẦM 4: Quên hệ số 2 trong thời gian
Sai: $t = \frac{v_0\sin\alpha}{g}$ ❌
Đúng: $t = \frac{2v_0\sin\alpha}{g}$ ✓
Giải thích: Đó chỉ là thời gian lên, còn phải cộng thời gian xuống
3. Kiểm tra nhanh kết quả
Kiểm tra 1: Giới hạn góc
- Khi $\alpha = 0°$: $L = 0$, $h_{max} = 0$, $t = 0$ ✓
- Khi $\alpha = 90°$: $L = 0$, $h_{max}$ cực đại, $t$ lớn nhất ✓
- Khi $\alpha = 45°$: $L$ cực đại ✓
Kiểm tra 2: Quan hệ $L$ và $h_{max}$
Với góc 45°: $L = 4h_{max}$
Nếu $L \neq 4h_{max}$ khi $\alpha = 45°$ → Sai!
Kiểm tra 3: Vận tốc chạm đất
Độ lớn vận tốc khi chạm đất phải bằng $v_0$
Nếu khác → Sai tính toán!
VII. BÀI TẬP MẪU
Bài 1: Tính tầm xa và độ cao
Đề bài: Ném một vật với vận tốc $v_0 = 20$ m/s, góc ném $\alpha = 60°$. Lấy $g = 10$ m/s². Tính: a) Tầm xa b) Độ cao cực đại
Lời giải:
Câu a) Tầm xa: $$L = \frac{v_0^2\sin 2\alpha}{g} = \frac{20^2 \times \sin(2 \times 60°)}{10}$$ $$= \frac{400 \times \sin 120°}{10} = \frac{400 \times \frac{\sqrt{3}}{2}}{10}$$ $$= \frac{200\sqrt{3}}{10} = 20\sqrt{3} \approx 34.64 \text{ m}$$
Câu b) Độ cao cực đại: $$h_{max} = \frac{v_0^2\sin^2\alpha}{2g} = \frac{20^2 \times (\sin 60°)^2}{2 \times 10}$$ $$= \frac{400 \times \left(\frac{\sqrt{3}}{2}\right)^2}{20} = \frac{400 \times 0.75}{20} = 15 \text{ m}$$
Đáp án:
- Tầm xa: 34.64 m
- Độ cao cực đại: 15 m
Bài 2: Tìm góc ném
Đề bài: Ném một vật với vận tốc $v_0 = 10$ m/s để đạt tầm xa 10 m. Tìm góc ném. Lấy $g = 10$ m/s².
Lời giải:
Từ công thức tầm xa: $$L = \frac{v_0^2\sin 2\alpha}{g}$$
Thay số: $$10 = \frac{10^2 \times \sin 2\alpha}{10}$$ $$10 = \frac{100\sin 2\alpha}{10}$$ $$10 = 10\sin 2\alpha$$ $$\sin 2\alpha = 1$$
Do $\sin 2\alpha = 1$ nên: $$2\alpha = 90° \Rightarrow \alpha = 45°$$
Đáp án: Góc ném là 45°
Bài 3: Tầm xa cực đại
Đề bài: Với vận tốc ban đầu $v_0 = 30$ m/s, tính tầm xa cực đại và góc ném tương ứng. Lấy $g = 10$ m/s².
Lời giải:
Góc ném để đạt tầm xa cực đại: $$\alpha = 45°$$
Tầm xa cực đại: $$L_{max} = \frac{v_0^2}{g} = \frac{30^2}{10} = \frac{900}{10} = 90 \text{ m}$$
Đáp án:
- Góc ném: 45°
- Tầm xa cực đại: 90 m
Bài 4: Thời gian bay
Đề bài: Ném vật với $v_0 = 20$ m/s, góc $\alpha = 30°$. Tính: a) Thời gian bay b) Thời gian đạt độ cao cực đại
Lời giải:
Câu a) Thời gian bay: $$t = \frac{2v_0\sin\alpha}{g} = \frac{2 \times 20 \times \sin 30°}{10}$$ $$= \frac{2 \times 20 \times 0.5}{10} = \frac{20}{10} = 2 \text{ giây}$$
Câu b) Thời gian đạt $h_{max}$: $$t_{h_{max}} = \frac{t}{2} = \frac{2}{2} = 1 \text{ giây}$$
Đáp án:
- Thời gian bay: 2 giây
- Thời gian đạt $h_{max}$: 1 giây
Bài 5: So sánh hai góc
Đề bài: Ném vật với $v_0 = 20$ m/s ở hai góc $25°$ và $65°$. So sánh tầm xa của hai lần ném.
Lời giải:
Kiểm tra tổng hai góc: $$25° + 65° = 90°$$
Hai góc bù nhau → Cho cùng tầm xa.
Kết luận: $L(25°) = L(65°)$
Giải thích: Do $\sin(2 \times 25°) = \sin 50°$ và $\sin(2 \times 65°) = \sin 130° = \sin 50°$
Bài 6: Tính vận tốc ban đầu
Đề bài: Ném xiên với góc $45°$, đạt tầm xa 50 m. Tính vận tốc ban đầu. Lấy $g = 10$ m/s².
Lời giải:
Với góc $45°$: $$L = \frac{v_0^2}{g}$$
Thay số: $$50 = \frac{v_0^2}{10}$$ $$v_0^2 = 500$$ $$v_0 = \sqrt{500} = 10\sqrt{5} \approx 22.36 \text{ m/s}$$
Đáp án: $v_0 \approx 22.36$ m/s
VIII. KẾT LUẬN
Bài viết đã trình bày đầy đủ công thức chuyển động ném xiên:
Ba công thức cốt lõi:
- Tầm xa: $L = \frac{v_0^2\sin 2\alpha}{g}$
- Độ cao cực đại: $h_{max} = \frac{v_0^2\sin^2\alpha}{2g}$
- Thời gian bay: $t = \frac{2v_0\sin\alpha}{g}$
Góc ném tối ưu: $\alpha = 45°$ cho $L_{max} = \frac{v_0^2}{g}$
Phân tích chuyển động: Ngang (thẳng đều) + Đứng (ném lên)
Bài tập: 6 bài mẫu có lời giải chi tiết
Ba công thức QUAN TRỌNG NHẤT
1. Tầm xa:
$$\boxed{L = \frac{v_0^2\sin 2\alpha}{g}}$$
Nhớ: Có $\sin 2\alpha$
2. Độ cao cực đại:
$$\boxed{h_{max} = \frac{v_0^2\sin^2\alpha}{2g}}$$
Nhớ: Có $\sin^2\alpha$ và hệ số $\frac{1}{2}$
3. Góc ném tối ưu:
$$\boxed{\alpha = 45° \Rightarrow L_{max} = \frac{v_0^2}{g}}$$
Nhớ: 45° là “góc vàng”
Điểm đặc biệt cần nhớ
Hai góc bù nhau: $$L(\alpha) = L(90° – \alpha)$$
Ví dụ: $L(30°) = L(60°)$
Quan hệ với góc 45°: $$L_{45°} = 4h_{max, 45°}$$

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
