Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ TỪ THÔNG
- 1. Từ thông là gì?
- 2. Các đại lượng liên quan
- II. CÔNG THỨC TỪ THÔNG
- 1. Công thức tổng quát
- 2. Các trường hợp đặc biệt
- 3. Công thức cho khung dây nhiều vòng
- 4. Minh họa hình học
- 5. Ví dụ minh họa
- III. ĐỊNH LUẬT FARADAY VỀ CẢM ỨNG ĐIỆN TỪ
- 1. Định luật Faraday
- 2. Công thức với nhiều vòng dây
- 3. Các cách làm thay đổi từ thông
- 4. Ví dụ ứng dụng định luật Faraday
- IV. CÔNG THỨC ĐẶC BIỆT: KHUNG DÂY QUAY TRONG TỪ TRƯỜNG
- 1. Từ thông tức thời
- 2. Suất điện động cảm ứng
- 3. Mối liên hệ với tần số
- 4. Ví dụ về khung dây quay
- V. BẢNG CÔNG THỨC TỔNG HỢP
- A. Công thức từ thông
- B. Định luật Faraday
- C. Khung dây quay trong từ trường
- D. Đơn vị đo
- VI. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Dấu hiệu nhận biết bài toán
- VII. BÀI TẬP MẪU
- VIII. KẾT LUẬN
- Lời khuyên học tập
I. GIỚI THIỆU VỀ TỪ THÔNG
1. Từ thông là gì?
Định nghĩa: Từ thông là đại lượng vật lý đặc trưng cho số đường sức từ xuyên qua một diện tích nhất định. Nói cách khác, từ thông đo “lượng” từ trường đi qua một bề mặt.
Ký hiệu: Φ (chữ cái Hy Lạp “phi”)
Đơn vị:
- Đơn vị chính: Wb (Weber)
- Đơn vị thay thế: T.m² (Tesla.mét vuông)
- Quy đổi: 1 Wb = 1 T.m²
Ý nghĩa vật lý:
- Từ thông lớn → Nhiều đường sức từ xuyên qua bề mặt
- Từ thông nhỏ → Ít đường sức từ xuyên qua bề mặt
- Từ thông = 0 → Không có đường sức từ nào xuyên qua
2. Các đại lượng liên quan
| Đại lượng | Ký hiệu | Đơn vị | Ý nghĩa |
|---|---|---|---|
| Từ thông | Φ | Wb (Weber) | Số đường sức từ qua diện tích S |
| Cảm ứng từ | B | T (Tesla) | Độ mạnh của từ trường tại một điểm |
| Diện tích | S | m² (mét vuông) | Diện tích bề mặt xét |
| Góc | α | độ (°) hoặc rad | Góc giữa $\vec{B}$ và vector pháp tuyến |
| Số vòng dây | N | (không đơn vị) | Số vòng dây của khung |
II. CÔNG THỨC TỪ THÔNG
1. Công thức tổng quát
Từ thông qua diện tích S trong từ trường đều:
$$\boxed{\Phi = BS\cos\alpha}$$
Hoặc viết dưới dạng tích vô hướng:
$$\boxed{\Phi = \vec{B} \cdot \vec{S} = BS\cos\alpha}$$
Trong đó:
- $\Phi$: từ thông qua diện tích S (đơn vị: Wb)
- $B$: cảm ứng từ (độ mạnh từ trường) (đơn vị: T)
- $S$: diện tích bề mặt xét (đơn vị: m²)
- $\alpha$: góc giữa vector cảm ứng từ $\vec{B}$ và vector pháp tuyến $\vec{n}$ của mặt phẳng
Lưu ý quan trọng:
- $\alpha$ là góc giữa $\vec{B}$ và vector pháp tuyến $\vec{n}$ của mặt phẳng
- $\alpha$ KHÔNG PHẢI là góc giữa $\vec{B}$ và mặt phẳng!
2. Các trường hợp đặc biệt
a) Mặt phẳng vuông góc với $\vec{B}$ (α = 0°):
Khi mặt phẳng đặt vuông góc với các đường sức từ:
$$\boxed{\Phi = BS\cos 0° = BS}$$
Đây là trường hợp từ thông CỰC ĐẠI
Giải thích: Mọi đường sức từ đều xuyên qua mặt phẳng nên từ thông đạt giá trị lớn nhất.
b) Mặt phẳng song song với $\vec{B}$ (α = 90°):
Khi mặt phẳng song song với các đường sức từ:
$$\boxed{\Phi = BS\cos 90° = 0}$$
Từ thông bằng 0 – Không có đường sức từ nào xuyên qua mặt phẳng.
Giải thích: Các đường sức từ đi song song với mặt phẳng nên không xuyên qua.
c) Mặt phẳng nghiêng góc α:
Trường hợp tổng quát khi mặt phẳng nghiêng một góc bất kỳ:
$$\boxed{\Phi = BS\cos\alpha}$$
Lưu ý: Nếu đề bài cho góc β giữa $\vec{B}$ và mặt phẳng thì: $$\alpha = 90° – \beta$$
3. Công thức cho khung dây nhiều vòng
Khung dây có N vòng:
$$\boxed{\Phi = NBS\cos\alpha}$$
Trong đó:
- $N$: số vòng dây của khung (không có đơn vị)
- Các đại lượng khác giống như trên
Giải thích: Khi khung có N vòng dây thì từ thông qua mỗi vòng sẽ cộng lại, do đó phải nhân với N.
4. Minh họa hình học
Để hiểu rõ hơn về góc α, xét hình vẽ sau:
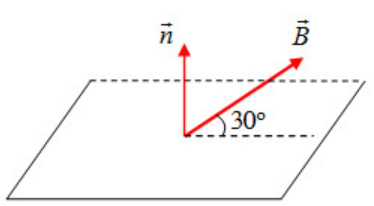
Quy tắc xác định:
- Vector pháp tuyến $\vec{n}$ vuông góc với mặt phẳng
- Góc α được đo từ $\vec{n}$ đến $\vec{B}$
- Nếu đề cho góc giữa $\vec{B}$ và mặt phẳng là β → $\alpha = 90° – \beta$
5. Ví dụ minh họa
Ví dụ 1: Tính từ thông cơ bản
Đề bài: Một khung dây phẳng có diện tích S = 200 cm² đặt trong từ trường đều có cảm ứng từ B = 0.5T. Mặt phẳng khung dây vuông góc với các đường sức từ. Tính từ thông qua khung dây.
Lời giải:
Bước 1: Đổi đơn vị
- S = 200 cm² = 200 × 10⁻⁴ m² = 0.02 m²
Bước 2: Xác định góc
- Mặt phẳng vuông góc với $\vec{B}$ → α = 0°
Bước 3: Áp dụng công thức $$\Phi = BS\cos\alpha = BS\cos 0°$$ $$\Phi = 0.5 \times 0.02 \times 1 = 0.01 \text{ Wb}$$
Kết luận: Từ thông qua khung dây là 0.01 Wb.
Ví dụ 2: Khung dây nghiêng
Đề bài: Khung dây như ví dụ 1 nhưng mặt phẳng khung hợp với $\vec{B}$ một góc 60°. Tính từ thông qua khung dây.
Lời giải:
Bước 1: Xác định góc α
- Góc giữa mặt phẳng và $\vec{B}$ là: β = 60°
- Góc giữa pháp tuyến và $\vec{B}$: α = 90° – 60° = 30°
Bước 2: Áp dụng công thức $$\Phi = BS\cos 30°$$ $$\Phi = 0.5 \times 0.02 \times \frac{\sqrt{3}}{2}$$ $$\Phi = 0.01 \times \frac{\sqrt{3}}{2}$$ $$\Phi = 0.01\sqrt{3} \approx 0.0173 \text{ Wb}$$
Kết luận: Từ thông giảm so với trường hợp vuông góc.
Ví dụ 3: Khung dây nhiều vòng
Đề bài: Một cuộn dây có 50 vòng, diện tích mỗi vòng S = 100 cm², đặt trong từ trường B = 0.4T. Mặt phẳng các vòng dây vuông góc với $\vec{B}$. Tính từ thông qua cuộn dây.
Lời giải:
Bước 1: Đổi đơn vị
- S = 100 cm² = 0.01 m²
Bước 2: Áp dụng công thức cho N vòng $$\Phi = NBS\cos 0°$$ $$\Phi = 50 \times 0.4 \times 0.01 \times 1$$ $$\Phi = 0.2 \text{ Wb}$$
Kết luận: Từ thông qua cuộn dây là 0.2 Wb.
III. ĐỊNH LUẬT FARADAY VỀ CẢM ỨNG ĐIỆN TỪ
1. Định luật Faraday
Phát biểu: Suất điện động cảm ứng xuất hiện trong một mạch kín tỉ lệ với tốc độ biến thiên của từ thông qua mạch đó.
Công thức:
$$\boxed{e = -\frac{\Delta\Phi}{\Delta t}}$$
Hoặc dạng vi phân (đạo hàm):
$$\boxed{e = -\frac{d\Phi}{dt}}$$
Trong đó:
- $e$: suất điện động cảm ứng (đơn vị: V – Volt)
- $\Delta\Phi$: độ biến thiên từ thông (đơn vị: Wb)
- $\Delta t$: khoảng thời gian biến thiên (đơn vị: s – giây)
- Dấu (−): tuân theo định luật Lenz (chiều dòng điện cảm ứng chống lại sự biến thiên từ thông)
Ý nghĩa:
- Từ thông biến thiên càng nhanh → suất điện động cảm ứng càng lớn
- Dấu âm thể hiện chiều của dòng điện cảm ứng (định luật Lenz)
2. Công thức với nhiều vòng dây
Khi khung dây có N vòng:
$$\boxed{e = -N\frac{\Delta\Phi}{\Delta t}}$$
Giải thích: Suất điện động trong mỗi vòng cộng lại nên phải nhân với N.
Chú ý: $\Delta\Phi$ ở đây là độ biến thiên từ thông qua MỘT vòng dây, không phải tổng.
3. Các cách làm thay đổi từ thông
Từ công thức $\Phi = BS\cos\alpha$, ta thấy từ thông có thể thay đổi theo 3 cách:
a) Thay đổi B (cảm ứng từ):
Cách thực hiện:
- Đưa nam châm lại gần hoặc ra xa cuộn dây
- Thay đổi cường độ dòng điện chạy qua nam châm điện
- Di chuyển khung dây ra vào vùng từ trường
Ví dụ: Đưa thanh nam châm lại gần cuộn dây → B tăng → Φ tăng → xuất hiện suất điện động cảm ứng
b) Thay đổi S (diện tích):
Cách thực hiện:
- Kéo giãn hoặc nén khung dây đàn hồi
- Thay đổi kích thước vòng dây
- Thu nhỏ hoặc mở rộng diện tích khung
Ví dụ: Kéo giãn khung dây → S tăng → Φ tăng → xuất hiện suất điện động cảm ứng
c) Thay đổi α (góc):
Cách thực hiện:
- Quay khung dây trong từ trường
- Thay đổi hướng của mặt phẳng khung
Ví dụ: Quay khung dây từ vị trí vuông góc (α = 0°) sang song song (α = 90°) với $\vec{B}$ → Φ giảm từ cực đại về 0 → xuất hiện suất điện động cảm ứng
Đây chính là nguyên lý hoạt động của máy phát điện!
4. Ví dụ ứng dụng định luật Faraday
Bài toán: Một khung dây có 100 vòng, diện tích mỗi vòng S = 0.01 m² đặt vuông góc trong từ trường. Cảm ứng từ B giảm đều từ 0.5T xuống 0.1T trong thời gian 0.2s. Tính suất điện động cảm ứng xuất hiện trong khung.
Lời giải:
Bước 1: Tính từ thông ban đầu (qua 1 vòng) $$\Phi_1 = BS = 0.5 \times 0.01 = 0.005 \text{ Wb}$$
Bước 2: Tính từ thông sau (qua 1 vòng) $$\Phi_2 = BS = 0.1 \times 0.01 = 0.001 \text{ Wb}$$
Bước 3: Tính độ biến thiên từ thông (qua 1 vòng) $$\Delta\Phi = \Phi_2 – \Phi_1 = 0.001 – 0.005 = -0.004 \text{ Wb}$$
Bước 4: Tính suất điện động cảm ứng $$|e| = \left|N\frac{\Delta\Phi}{\Delta t}\right| = \left|100 \times \frac{-0.004}{0.2}\right|$$ $$|e| = \left|100 \times (-0.02)\right| = 2 \text{ V}$$
Kết luận: Suất điện động cảm ứng có độ lớn là 2V.
Giải thích: Dấu âm trong $\Delta\Phi$ cho biết từ thông giảm, còn độ lớn suất điện động là 2V.
IV. CÔNG THỨC ĐẶC BIỆT: KHUNG DÂY QUAY TRONG TỪ TRƯỜNG
1. Từ thông tức thời
Bài toán: Khung dây phẳng quay đều trong từ trường đều với tốc độ góc ω.
Từ thông tại thời điểm t:
$$\boxed{\Phi = BS\cos(\omega t) = \Phi_0\cos(\omega t)}$$
Trong đó:
- $\Phi_0 = BS$: từ thông cực đại (khi khung vuông góc với $\vec{B}$)
- $\omega$: tốc độ góc (đơn vị: rad/s)
- $t$: thời gian (đơn vị: s)
- $\omega t$: góc quay được tại thời điểm t
Giải thích: Khi khung quay, góc α thay đổi theo thời gian: $\alpha = \omega t$
2. Suất điện động cảm ứng
Áp dụng định luật Faraday:
$$e = -\frac{d\Phi}{dt} = -\frac{d[BS\cos(\omega t)]}{dt}$$
Tính đạo hàm:
$$e = -BS \times (-\omega\sin(\omega t))$$
$$\boxed{e = BS\omega\sin(\omega t) = E_0\sin(\omega t)}$$
Trong đó:
- $E_0 = BS\omega$: suất điện động cực đại (biên độ)
- Với khung N vòng: $E_0 = NBS\omega$
Đây chính là dòng điện xoay chiều – nguyên lý máy phát điện!
3. Mối liên hệ với tần số
Tần số f và tốc độ góc ω:
$$\omega = 2\pi f$$
Do đó:
- $E_0 = BS\omega = BS \cdot 2\pi f = 2\pi fBS$
- Với N vòng: $E_0 = 2\pi fNBS$
Công thức thường dùng:
$$\boxed{E_0 = 2\pi fNBS}$$
4. Ví dụ về khung dây quay
Đề bài: Một khung dây có 200 vòng, diện tích mỗi vòng S = 0.04 m², quay đều với tần số f = 50 Hz trong từ trường đều có cảm ứng từ B = 0.2T. Trục quay vuông góc với đường sức từ. Tính: a) Từ thông cực đại qua khung b) Suất điện động cực đại trong khung
Lời giải:
Câu a) Từ thông cực đại:
Từ thông cực đại khi khung vuông góc với $\vec{B}$: $$\Phi_0 = NBS$$ $$\Phi_0 = 200 \times 0.2 \times 0.04$$ $$\Phi_0 = 1.6 \text{ Wb}$$
Câu b) Suất điện động cực đại:
Cách 1: Dùng tần số $$E_0 = 2\pi fNBS$$ $$E_0 = 2\pi \times 50 \times 200 \times 0.2 \times 0.04$$ $$E_0 = 2\pi \times 50 \times 1.6$$ $$E_0 = 160\pi \approx 502.4 \text{ V}$$
Cách 2: Dùng tốc độ góc
- Tốc độ góc: $\omega = 2\pi f = 2\pi \times 50 = 100\pi$ rad/s
- $E_0 = NBS\omega = 1.6 \times 100\pi = 160\pi \approx 502.4$ V
Kết luận:
- Từ thông cực đại: 1.6 Wb
- Suất điện động cực đại: 160π ≈ 502.4 V
V. BẢNG CÔNG THỨC TỔNG HỢP
A. Công thức từ thông
| Trường hợp | Công thức | Điều kiện |
|---|---|---|
| Tổng quát | $\Phi = BS\cos\alpha$ | Góc α bất kỳ |
| Vuông góc | $\Phi = BS$ | $\alpha = 0°$ (cực đại) |
| Song song | $\Phi = 0$ | $\alpha = 90°$ |
| N vòng dây | $\Phi = NBS\cos\alpha$ | Khung có N vòng |
| Góc β với mặt phẳng | $\Phi = BS\cos(90° – \beta) = BS\sin\beta$ | Đổi góc |
B. Định luật Faraday
| Công thức | Ý nghĩa | Đơn vị |
|---|---|---|
| $e = -\frac{\Delta\Phi}{\Delta t}$ | Suất điện động cảm ứng (1 vòng) | V (Volt) |
| $e = -N\frac{\Delta\Phi}{\Delta t}$ | Suất điện động (N vòng dây) | V (Volt) |
| $\Delta\Phi = \Phi_2 – \Phi_1$ | Độ biến thiên từ thông | Wb (Weber) |
C. Khung dây quay trong từ trường
| Đại lượng | Công thức | Ghi chú |
|---|---|---|
| Từ thông tức thời | $\Phi = \Phi_0\cos(\omega t)$ | Biến thiên theo thời gian |
| Từ thông cực đại | $\Phi_0 = BS$ hoặc $NBS$ | Khi α = 0° |
| Suất điện động | $e = E_0\sin(\omega t)$ | Dòng xoay chiều |
| Suất đtđ cực đại | $E_0 = BS\omega$ hoặc $NBS\omega$ | |
| Với tần số | $E_0 = 2\pi fNBS$ | $\omega = 2\pi f$ |
D. Đơn vị đo
| Đại lượng | Ký hiệu | Đơn vị | Quy đổi |
|---|---|---|---|
| Từ thông | Φ | Wb (Weber) | 1 Wb = 1 T.m² |
| Cảm ứng từ | B | T (Tesla) | 1 T = 1 Wb/m² |
| Diện tích | S | m² | 1 m² = 10⁴ cm² |
| Suất điện động | e | V (Volt) | |
| Tốc độ góc | ω | rad/s | $\omega = 2\pi f$ |
| Tần số | f | Hz (Hertz) |
VI. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
✅ Công thức cốt lõi:
“B nhân S nhân cos alpha”
$$\Phi = BS\cos\alpha$$
Đây là công thức QUAN TRỌNG NHẤT cần nhớ!
✅ Nhớ góc α:
QUY TẮC VÀNG:
- α là góc giữa $\vec{B}$ và vector pháp tuyến $\vec{n}$ (không phải mặt phẳng!)
- Nếu đề cho góc β giữa $\vec{B}$ và mặt phẳng → $\alpha = 90° – \beta$
Cách nhớ:
- “Pháp tuyến vuông góc với mặt phẳng”
- “α + β = 90°”
✅ Từ thông cực đại khi:
Mặt phẳng vuông góc với $\vec{B}$ (các đường sức từ xuyên thẳng qua)
- $\alpha = 0°$
- $\cos\alpha = 1$
- $\Phi_{max} = BS$
✅ Từ thông bằng 0 khi:
Mặt phẳng song song với $\vec{B}$ (không có đường sức nào xuyên qua)
- $\alpha = 90°$
- $\cos\alpha = 0$
- $\Phi = 0$
✅ Phân biệt cos và sin:
- Từ thông dùng cos: $\Phi = BS\cos\alpha$
- Suất điện động (khung quay) dùng sin: $e = E_0\sin(\omega t)$
Cách nhớ:
- “Từ thông → cosin”
- “Suất điện động → sin”
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm góc α
Sai: α là góc giữa $\vec{B}$ và mặt phẳng ❌
Đúng: α là góc giữa $\vec{B}$ và pháp tuyến của mặt phẳng ✓
Hậu quả: Sử dụng sai giá trị cos → kết quả sai hoàn toàn
❌ SAI LẦM 2: Quên đổi đơn vị
Sai: S = 200 cm² (dùng luôn không đổi) ❌
Đúng: S = 200 cm² = 0.02 m² ✓
Lưu ý: Luôn đổi về đơn vị chuẩn: m², T, s
❌ SAI LẦM 3: Quên nhân N
Sai: Khung 100 vòng nhưng tính $\Phi = BS\cos\alpha$ ❌
Đúng: $\Phi = NBS\cos\alpha$ với N = 100 ✓
❌ SAI LẦM 4: Nhầm công thức $\Phi_0$ và $E_0$
Sai:
- $\Phi_0 = BS\omega$ ❌
- $E_0 = BS$ ❌
Đúng:
- $\Phi_0 = BS$ (không có ω) ✓
- $E_0 = BS\omega$ (có ω) ✓
Cách nhớ: Suất điện động liên quan đến tốc độ biến thiên nên có ω
❌ SAI LẦM 5: Nhầm cos và sin
Sai:
- Từ thông: $\Phi = BS\sin\alpha$ ❌
- Suất điện động: $e = E_0\cos(\omega t)$ ❌
Đúng:
- Từ thông: $\Phi = BS\cos\alpha$ ✓
- Suất điện động (khung quay): $e = E_0\sin(\omega t)$ ✓
3. Dấu hiệu nhận biết bài toán
Bài toán tính từ thông:
- Cho B, S, α → Dùng $\Phi = BS\cos\alpha$
- Khung nhiều vòng → Nhớ nhân N
Bài toán suất điện động:
- Cho từ thông biến thiên → Dùng $e = -\frac{\Delta\Phi}{\Delta t}$
- Khung quay đều → Dùng $E_0 = NBS\omega$ hoặc $E_0 = 2\pi fNBS$
Bài toán khung quay:
- Cho tần số f hoặc tốc độ góc ω
- Yêu cầu tìm $E_0$ → Dùng $E_0 = NBS\omega$
VII. BÀI TẬP MẪU
Bài tập 1: Tính từ thông cơ bản
Đề bài: Một khung dây hình vuông cạnh 20cm đặt trong từ trường đều có cảm ứng từ B = 0.4T. Mặt phẳng khung hợp với các đường sức từ một góc 30°. Tính từ thông qua khung dây.
Lời giải:
Bước 1: Tính diện tích khung $$S = a^2 = (0.2)^2 = 0.04 \text{ m}^2$$
Bước 2: Xác định góc α
- Góc giữa mặt phẳng và $\vec{B}$: β = 30°
- Góc giữa pháp tuyến và $\vec{B}$: $\alpha = 90° – 30° = 60°$
Bước 3: Tính từ thông $$\Phi = BS\cos\alpha$$ $$\Phi = 0.4 \times 0.04 \times \cos 60°$$ $$\Phi = 0.4 \times 0.04 \times 0.5$$ $$\Phi = 0.008 \text{ Wb}$$
Kết luận: Từ thông qua khung dây là 0.008 Wb = 8 × 10⁻³ Wb.
Bài tập 2: Suất điện động cảm ứng
Đề bài: Từ thông qua một khung dây tăng đều từ 0.2 Wb đến 0.8 Wb trong khoảng thời gian 0.1s. Tính suất điện động cảm ứng xuất hiện trong khung.
Lời giải:
Bước 1: Tính độ biến thiên từ thông $$\Delta\Phi = \Phi_2 – \Phi_1 = 0.8 – 0.2 = 0.6 \text{ Wb}$$
Bước 2: Tính suất điện động cảm ứng $$|e| = \left|\frac{\Delta\Phi}{\Delta t}\right| = \frac{0.6}{0.1} = 6 \text{ V}$$
Kết luận: Suất điện động cảm ứng có độ lớn 6V.
Giải thích: Dấu trừ trong công thức Faraday chỉ hướng của suất điện động (định luật Lenz), ta chỉ quan tâm độ lớn nên lấy trị tuyệt đối.
Bài tập 3: Khung dây quay
Đề bài: Một khung dây gồm 50 vòng, diện tích mỗi vòng S = 0.05 m² quay đều với tần số f = 60 Hz trong từ trường đều có cảm ứng từ B = 0.1T. Trục quay vuông góc với đường sức từ. Tính suất điện động cực đại trong khung.
Lời giải:
Cách 1: Dùng công thức với tần số $$E_0 = 2\pi fNBS$$ $$E_0 = 2\pi \times 60 \times 50 \times 0.1 \times 0.05$$ $$E_0 = 2\pi \times 60 \times 0.25$$ $$E_0 = 30\pi \approx 94.2 \text{ V}$$
Cách 2: Dùng tốc độ góc
- Tốc độ góc: $\omega = 2\pi f = 2\pi \times 60 = 120\pi$ rad/s
- $E_0 = NBS\omega = 50 \times 0.1 \times 0.05 \times 120\pi$
- $E_0 = 30\pi \approx 94.2$ V
Kết luận: Suất điện động cực đại là 30π ≈ 94.2 V.
Bài tập 4: Thay đổi từ trường
Đề bài: Một khung dây phẳng có 100 vòng, diện tích mỗi vòng S = 0.02 m² đặt vuông góc với các đường sức từ. Cảm ứng từ tăng đều từ 0 đến 0.5T trong thời gian 0.25s. Tính suất điện động cảm ứng xuất hiện trong khung.
Lời giải:
Bước 1: Tính từ thông ban đầu (qua 1 vòng) $$\Phi_1 = BS = 0 \times 0.02 = 0 \text{ Wb}$$
Bước 2: Tính từ thông sau (qua 1 vòng) $$\Phi_2 = BS = 0.5 \times 0.02 = 0.01 \text{ Wb}$$
Bước 3: Tính độ biến thiên từ thông (qua 1 vòng) $$\Delta\Phi = \Phi_2 – \Phi_1 = 0.01 – 0 = 0.01 \text{ Wb}$$
Bước 4: Tính suất điện động cảm ứng $$|e| = \left|N\frac{\Delta\Phi}{\Delta t}\right| = \left|100 \times \frac{0.01}{0.25}\right|$$ $$|e| = 100 \times 0.04 = 4 \text{ V}$$
Kết luận: Suất điện động cảm ứng có độ lớn 4V.
VIII. KẾT LUẬN
Bài viết đã trình bày đầy đủ kiến thức về từ thông cho chương trình Vật lý 11:
Khái niệm từ thông:
- Đại lượng đặc trưng cho số đường sức từ xuyên qua diện tích
- Đơn vị: Wb (Weber) = T.m²
Công thức từ thông:
- Tổng quát: $\Phi = BS\cos\alpha$
- Vuông góc: $\Phi = BS$ (cực đại)
- Song song: $\Phi = 0$
- N vòng dây: $\Phi = NBS\cos\alpha$
Định luật Faraday:
- $e = -\frac{\Delta\Phi}{\Delta t}$ (1 vòng)
- $e = -N\frac{\Delta\Phi}{\Delta t}$ (N vòng)
Khung dây quay:
- Từ thông: $\Phi = \Phi_0\cos(\omega t)$
- Suất điện động: $e = E_0\sin(\omega t)$
- Suất đtđ cực đại: $E_0 = NBS\omega = 2\pi fNBS$
Lời khuyên học tập
📌 Học thuộc công thức $\Phi = BS\cos\alpha$ – đây là nền tảng
📌 Phân biệt rõ góc α – góc giữa $\vec{B}$ và pháp tuyến, không phải mặt phẳng
📌 Nhớ quy tắc cos/sin:
- Từ thông → cosα
- Suất điện động (khung quay) → sinωt
📌 Chú ý đơn vị: Luôn đổi về m², T, s trước khi tính
📌 Luyện tập nhiều: Làm đủ các dạng bài để nắm vững
📌 Hiểu bản chất: Từ thông lớn khi nhiều đường sức từ xuyên qua

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
