Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ GIAO THOA ÁNH SÁNG
- 1. Giao thoa ánh sáng là gì?
- 2. Sơ đồ thí nghiệm Young
- 3. Các đại lượng trong thí nghiệm
- II. CÔNG THỨC KHOẢNG VÂN
- 1. Công thức tính khoảng vân
- 2. Tính các đại lượng từ khoảng vân
- 3. Ví dụ minh họa chi tiết
- 4. Khoảng vân với nhiều bước sóng
- III. CÔNG THỨC VỊ TRÍ VÂN SÁNG, VÂN TỐI
- 1. Điều kiện giao thoa – Hiệu đường đi
- 2. Vị trí vân sáng
- 3. Vị trí vân tối
- 4. Khoảng cách giữa các vân
- 5. Xác định bậc k và loại vân
- IV. CÔNG THỨC ĐẾM SỐ VÂN
- 1. Số vân sáng trên màn
- 2. Số vân tối trên màn
- 3. Số vân trên đoạn [x₁, x₂]
- 4. Số vân với ánh sáng trắng
- V. TRƯỜNG HỢP ĐẶC BIỆT VÀ BÀI TOÁN NÂNG CAO
- 1. Thay đổi môi trường
- 2. Di chuyển màn hoặc khe
- 3. Đặt tấm mỏng trước một khe
- 4. Vân trùng nhau (hai bước sóng)
- VI. BẢNG CÔNG THỨC TỔNG HỢP
- A. Khoảng vân
- B. Vị trí vân
- C. Đếm số vân
- D. Trường hợp đặc biệt
- VII. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Kiểm tra kết quả
- 4. Bảng giá trị bước sóng tham khảo
- VIII. BÀI TẬP MẪU
- IX. KẾT LUẬN
- Công thức QUAN TRỌNG NHẤT
I. GIỚI THIỆU VỀ GIAO THOA ÁNH SÁNG
1. Giao thoa ánh sáng là gì?
Định nghĩa: Giao thoa ánh sáng là hiện tượng xảy ra khi hai sóng ánh sáng kết hợp (cùng tần số, có độ lệch pha không đổi theo thời gian) gặp nhau và tạo ra sự phân bố cường độ sáng không đều trên màn quan sát, với các vùng sáng (vân sáng) và vùng tối (vân tối) xen kẽ đều đặn.
Thí nghiệm Young (1801): Đây là thí nghiệm kinh điển và quan trọng nhất trong việc chứng minh tính chất sóng của ánh sáng. Thomas Young đã sử dụng một nguồn sáng chiếu qua hai khe hẹp đặt song song, rất gần nhau, và quan sát được hệ vân giao thoa trên màn.
Ý nghĩa lịch sử:
- Chứng minh ánh sáng có tính chất sóng (trước đó Newton cho rằng ánh sáng là hạt)
- Cho phép đo được bước sóng ánh sáng
- Mở đường cho lý thuyết sóng ánh sáng hiện đại
Điều kiện để có giao thoa:
- Hai nguồn sáng phải là hai nguồn kết hợp: cùng tần số (cùng màu), có độ lệch pha không đổi theo thời gian
- Trong thực tế, dùng một nguồn sáng chiếu qua hai khe để tạo hai nguồn kết hợp
2. Sơ đồ thí nghiệm Young
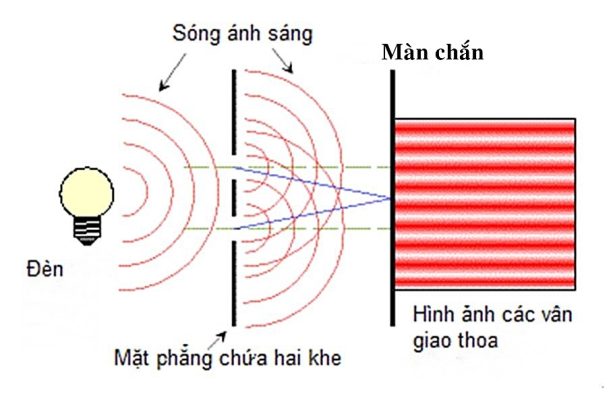
Giải thích:
- Nguồn S phát ánh sáng đơn sắc (một màu, một bước sóng)
- Ánh sáng qua khe S, sau đó chia thành hai chùm qua S₁ và S₂
- S₁ và S₂ trở thành hai nguồn kết hợp
- Hai sóng từ S₁ và S₂ giao thoa trên màn, tạo hệ vân sáng tối
3. Các đại lượng trong thí nghiệm
| Đại lượng | Ký hiệu | Đơn vị | Ý nghĩa |
|---|---|---|---|
| Bước sóng | $\lambda$ | m, nm, μm | Bước sóng ánh sáng (đơn sắc) |
| Khoảng cách hai khe | $a$ | m, mm | Khoảng cách S₁S₂ |
| Khoảng cách đến màn | $D$ | m, cm | Từ mặt phẳng chứa 2 khe đến màn |
| Khoảng vân | $i$ | m, mm | Khoảng cách giữa 2 vân sáng (hoặc 2 vân tối) liên tiếp |
| Vị trí vân | $x$ | m, mm | Tọa độ của vân trên màn (x = 0 tại vân trung tâm) |
| Hiệu đường đi | $\delta$ | m | $\delta = d_2 – d_1$ |
Đơn vị thường dùng:
- Bước sóng: 1 nm (nanomét) = $10^{-9}$ m
- Khoảng cách: 1 mm (milimét) = $10^{-3}$ m
- Khoảng cách: 1 μm (micromét) = $10^{-6}$ m
II. CÔNG THỨC KHOẢNG VÂN
1. Công thức tính khoảng vân
📌 Công thức QUAN TRỌNG NHẤT trong giao thoa ánh sáng:
$$\boxed{i = \frac{\lambda D}{a}}$$
Trong đó:
- $i$: khoảng vân (m, mm, cm) – khoảng cách giữa hai vân sáng (hoặc hai vân tối) liên tiếp
- $\lambda$: bước sóng ánh sáng (m, nm, μm)
- $D$: khoảng cách từ mặt phẳng chứa hai khe đến màn (m, cm)
- $a$: khoảng cách giữa hai khe S₁ và S₂ (m, mm)
Ý nghĩa vật lý:
- Khoảng vân đặc trưng cho độ rộng của hệ vân giao thoa
- Khoảng vân càng lớn, các vân càng rộng, dễ quan sát
- Khoảng vân phụ thuộc vào: bước sóng λ, khoảng cách D và khoảng cách hai khe a
Các yếu tố ảnh hưởng:
- $\lambda$ tăng → $i$ tăng (ánh sáng đỏ có khoảng vân lớn hơn ánh sáng tím)
- $D$ tăng → $i$ tăng (màn xa hơn, khoảng vân rộng hơn)
- $a$ tăng → $i$ giảm (hai khe xa nhau, khoảng vân hẹp hơn)
Lưu ý quan trọng về đơn vị:
Phải đổi tất cả về cùng hệ đơn vị (thường là mét):
- 1 nm = $10^{-9}$ m
- 1 μm = $10^{-6}$ m
- 1 mm = $10^{-3}$ m
- 1 cm = $10^{-2}$ m
Ví dụ đổi đơn vị:
- 600 nm = $600 \times 10^{-9}$ m = $6 \times 10^{-7}$ m
- 0.5 mm = $0.5 \times 10^{-3}$ m = $5 \times 10^{-4}$ m
2. Tính các đại lượng từ khoảng vân
Từ công thức $i = \frac{\lambda D}{a}$, ta có thể tính các đại lượng khác:
Tính bước sóng λ:
$$\boxed{\lambda = \frac{ia}{D}}$$
Ứng dụng: Đo bước sóng ánh sáng khi biết i, a, D.
Tính khoảng cách hai khe a:
$$\boxed{a = \frac{\lambda D}{i}}$$
Tính khoảng cách đến màn D:
$$\boxed{D = \frac{ia}{\lambda}}$$
3. Ví dụ minh họa chi tiết
Bài toán 1: Trong thí nghiệm Young về giao thoa ánh sáng, sử dụng ánh sáng đơn sắc có bước sóng $\lambda = 600$ nm. Khoảng cách giữa hai khe là $a = 1$ mm, khoảng cách từ hai khe đến màn là $D = 2$ m. Tính khoảng vân?
Lời giải:
Bước 1: Đổi đơn vị về mét
- $\lambda = 600$ nm = $600 \times 10^{-9}$ m = $6 \times 10^{-7}$ m
- $a = 1$ mm = $10^{-3}$ m = $0.001$ m
- $D = 2$ m
Bước 2: Áp dụng công thức $$i = \frac{\lambda D}{a} = \frac{6 \times 10^{-7} \times 2}{10^{-3}}$$
Bước 3: Tính toán $$i = \frac{12 \times 10^{-7}}{10^{-3}} = 12 \times 10^{-7} \times 10^{3} = 12 \times 10^{-4} \text{ m}$$
$$i = 1.2 \times 10^{-3} \text{ m} = 1.2 \text{ mm}$$
Kết luận: Khoảng vân là 1.2 mm.
Bài toán 2: Trong một thí nghiệm giao thoa, khoảng vân đo được là $i = 0.8$ mm, khoảng cách hai khe $a = 2$ mm, khoảng cách đến màn $D = 1.6$ m. Tính bước sóng ánh sáng?
Lời giải:
$$\lambda = \frac{ia}{D} = \frac{0.8 \times 10^{-3} \times 2 \times 10^{-3}}{1.6}$$
$$= \frac{1.6 \times 10^{-6}}{1.6} = 10^{-6} \text{ m} = 1000 \text{ nm}$$
Đây là ánh sáng hồng ngoại (vượt quá vùng nhìn thấy).
4. Khoảng vân với nhiều bước sóng
Khi dùng ánh sáng trắng (hỗn hợp của nhiều bước sóng từ 380 nm đến 760 nm):
Mỗi thành phần đơn sắc tạo một hệ vân riêng với khoảng vân khác nhau:
$$i = \frac{\lambda D}{a}$$
Nhận xét:
- Ánh sáng đỏ ($\lambda_{đỏ} \approx 750$ nm): $i_{đỏ}$ lớn nhất (khoảng vân rộng nhất)
- Ánh sáng tím ($\lambda_{tím} \approx 400$ nm): $i_{tím}$ nhỏ nhất (khoảng vân hẹp nhất)
Tỉ lệ khoảng vân:
$$\boxed{\frac{i_1}{i_2} = \frac{\lambda_1}{\lambda_2}}$$
Khoảng vân tỉ lệ thuận với bước sóng.
Ví dụ: So sánh khoảng vân của ánh sáng đỏ ($\lambda_đ = 750$ nm) và ánh sáng lục ($\lambda_l = 500$ nm).
$$\frac{i_{đỏ}}{i_{lục}} = \frac{750}{500} = 1.5$$
Khoảng vân của ánh sáng đỏ gấp 1.5 lần khoảng vân của ánh sáng lục.
Hệ quả:
- Vân trung tâm (k = 0) của tất cả các màu trùng nhau → vân trung tâm màu trắng
- Các vân bậc cao, các màu lệch nhau → tạo quang phổ màu sắc
III. CÔNG THỨC VỊ TRÍ VÂN SÁNG, VÂN TỐI
1. Điều kiện giao thoa – Hiệu đường đi
Hiệu đường đi là hiệu số khoảng cách từ hai khe đến một điểm M trên màn:
$$\delta = d_2 – d_1$$
Trong đó:
- $d_1$: khoảng cách từ khe S₁ đến điểm M
- $d_2$: khoảng cách từ khe S₂ đến điểm M
Công thức tính hiệu đường đi:
$$\boxed{\delta = \frac{ax}{D}}$$
Trong đó:
- $x$: tọa độ của điểm M trên màn (chọn gốc O tại vân trung tâm, dương về phía S₂)
- $a$: khoảng cách hai khe
- $D$: khoảng cách từ hai khe đến màn
Chứng minh:
Khi D >> a và D >> x (điều kiện thực tế luôn thỏa mãn): $$\delta \approx \frac{ax}{D}$$
2. Vị trí vân sáng
Điều kiện để có vân sáng tại M:
Hiệu đường đi phải bằng số nguyên lần bước sóng:
$$\delta = k\lambda \quad (k \in \mathbb{Z})$$
Trong đó $k$ là bậc giao thoa: $k = 0, \pm 1, \pm 2, \pm 3, …$
📌 Công thức vị trí vân sáng:
$$\boxed{x_s = k\frac{\lambda D}{a} = ki}$$
Giải thích:
- $k = 0$: Vân sáng trung tâm (tại O, $x = 0$)
- $k = \pm 1$: Vân sáng bậc 1 (hai bên vân trung tâm)
- $k = \pm 2$: Vân sáng bậc 2
- $k = \pm 3$: Vân sáng bậc 3
- …
Tính chất:
- Các vân sáng phân bố đối xứng qua vân trung tâm
- Khoảng cách giữa hai vân sáng liên tiếp bằng $i$
- Vân sáng bậc $k$ có tọa độ: $x = \pm ki$
Ví dụ: Với $i = 1.2$ mm
| Bậc k | Vị trí (mm) |
|---|---|
| 0 | 0 (vân trung tâm) |
| ±1 | ±1.2 |
| ±2 | ±2.4 |
| ±3 | ±3.6 |
| ±4 | ±4.8 |
3. Vị trí vân tối
Điều kiện để có vân tối tại M:
Hiệu đường đi phải bằng số nửa nguyên lẻ lần bước sóng:
$$\delta = \left(k + \frac{1}{2}\right)\lambda = (k + 0.5)\lambda$$
Trong đó $k = 0, \pm 1, \pm 2, \pm 3, …$
📌 Công thức vị trí vân tối:
$$\boxed{x_t = \left(k + \frac{1}{2}\right)\frac{\lambda D}{a} = \left(k + \frac{1}{2}\right)i = (k + 0.5)i}$$
Giải thích:
- $k = 0$: Vân tối thứ nhất (hai bên sát vân trung tâm), tọa độ $x = \pm 0.5i$
- $k = \pm 1$: Vân tối thứ hai, tọa độ $x = \pm 1.5i$
- $k = \pm 2$: Vân tối thứ ba, tọa độ $x = \pm 2.5i$
- …
Tính chất:
- Các vân tối nằm xen kẽ giữa các vân sáng
- Khoảng cách giữa hai vân tối liên tiếp bằng $i$
- Vân tối đối xứng qua vân trung tâm
Ví dụ: Với $i = 1.2$ mm
| Bậc k | Vị trí (mm) |
|---|---|
| 0 | ±0.6 (vân tối thứ 1) |
| ±1 | ±1.8 (vân tối thứ 2) |
| ±2 | ±3.0 (vân tối thứ 3) |
| ±3 | ±4.2 (vân tối thứ 4) |
4. Khoảng cách giữa các vân
Giữa hai vân sáng liên tiếp:
$$\Delta x = x_{k+1} – x_k = (k+1)i – ki = i$$
Giữa hai vân tối liên tiếp:
$$\Delta x = \left(k + \frac{3}{2}\right)i – \left(k + \frac{1}{2}\right)i = i$$
Giữa vân sáng và vân tối gần nhau nhất:
$$\Delta x = \left|x_s – x_t\right| = \left|ki – (k + 0.5)i\right| = 0.5i = \frac{i}{2}$$
Kết luận:
- Hai vân cùng loại liên tiếp cách nhau $i$
- Vân sáng và vân tối gần nhau cách nhau $\frac{i}{2}$
5. Xác định bậc k và loại vân
Cho vị trí x, xác định vân:
Bước 1: Tính $$k = \frac{x}{i}$$
Bước 2: Phân tích:
- Nếu $k$ là số nguyên (0, ±1, ±2, …) → Vân sáng bậc k
- Nếu $k$ là số nửa nguyên (±0.5, ±1.5, ±2.5, …) → Vân tối
- Nếu $k$ không nguyên, không nửa nguyên → Điểm nằm giữa vân sáng và vân tối
Ví dụ 1: Tại $x = 3.6$ mm, $i = 1.2$ mm
$$k = \frac{3.6}{1.2} = 3$$
→ Vân sáng bậc 3 ✓
Ví dụ 2: Tại $x = 2.7$ mm, $i = 1.2$ mm
$$k = \frac{2.7}{1.2} = 2.25$$
→ Không phải vân sáng, không phải vân tối, nằm giữa vân sáng bậc 2 ($x = 2.4$ mm) và vân tối ($x = 3.0$ mm)
IV. CÔNG THỨC ĐẾM SỐ VÂN
1. Số vân sáng trên màn
Bài toán: Trên màn có độ rộng $L$ (đối xứng qua vân trung tâm), đếm số vân sáng quan sát được?
Phương pháp:
Điều kiện vân sáng quan sát được: $$|x_s| \leq \frac{L}{2}$$
Thay $x_s = ki$: $$|ki| \leq \frac{L}{2}$$
$$|k| \leq \frac{L}{2i}$$
Tìm bậc cực đại: $$k_{max} = \left\lfloor\frac{L}{2i}\right\rfloor$$
Ký hiệu $\lfloor x \rfloor$ là phần nguyên của $x$ (làm tròn xuống).
📌 Công thức số vân sáng:
$$\boxed{N_s = 2k_{max} + 1}$$
Giải thích:
- Có $k_{max}$ vân sáng bên phải (k = 1, 2, …, $k_{max}$)
- Có $k_{max}$ vân sáng bên trái (k = -1, -2, …, $-k_{max}$)
- Có 1 vân sáng trung tâm (k = 0)
- Tổng: $N_s = k_{max} + k_{max} + 1 = 2k_{max} + 1$
Ví dụ 1: Màn rộng $L = 10$ mm, khoảng vân $i = 1.2$ mm. Đếm số vân sáng?
Lời giải: $$k_{max} = \left\lfloor\frac{10}{2 \times 1.2}\right\rfloor = \left\lfloor\frac{10}{2.4}\right\rfloor = \left\lfloor 4.17 \right\rfloor = 4$$
$$N_s = 2 \times 4 + 1 = 9 \text{ vân sáng}$$
Ví dụ 2: Màn rộng $L = 15$ mm, $i = 2$ mm. Đếm số vân sáng?
$$k_{max} = \left\lfloor\frac{15}{4}\right\rfloor = \left\lfloor 3.75 \right\rfloor = 3$$
$$N_s = 2 \times 3 + 1 = 7 \text{ vân sáng}$$
2. Số vân tối trên màn
Điều kiện vân tối quan sát được: $$\left|x_t\right| = \left|\left(k + \frac{1}{2}\right)i\right| \leq \frac{L}{2}$$
$$\left|k + \frac{1}{2}\right| \leq \frac{L}{2i}$$
Tìm k cực đại: $$k’_{max} = \left\lfloor\frac{L}{2i} – 0.5\right\rfloor$$
Hoặc: $$k’_{max} = \left\lfloor\frac{L}{2i} + 0.5\right\rfloor$$
📌 Công thức số vân tối:
$$\boxed{N_t = 2(k’_{max} + 1)}$$
Hoặc đơn giản hơn: $$N_t = 2\left\lfloor\frac{L}{2i} + 0.5\right\rfloor$$
Giải thích: Có $k’_{max} + 1$ vân tối mỗi bên (k = 0, 1, 2, …, $k’_{max}$)
Ví dụ 1: Với $L = 10$ mm, $i = 1.2$ mm
$$k’_{max} = \left\lfloor\frac{10}{2.4} + 0.5\right\rfloor = \left\lfloor 4.67 \right\rfloor = 4$$
$$N_t = 2 \times 4 = 8 \text{ vân tối}$$
Kiểm tra: Có 9 vân sáng và 8 vân tối, sắp xếp: S-T-S-T-S-T-S-T-S-T-S-T-S-T-S-T-S ✓
Nhận xét:
- Số vân sáng luôn là số lẻ (vì có vân trung tâm k = 0)
- Số vân tối luôn là số chẵn (đối xứng hai bên)
- Thường: $N_t = N_s – 1$ hoặc $N_t = N_s + 1$
3. Số vân trên đoạn [x₁, x₂]
Bài toán: Đếm số vân sáng (hoặc vân tối) trên đoạn từ $x_1$ đến $x_2$ trên màn.
Phương pháp đếm vân sáng:
Bước 1: Tính bậc tương ứng: $$k_1 = \frac{x_1}{i}, \quad k_2 = \frac{x_2}{i}$$
Bước 2: Làm tròn:
- Làm tròn lên $k_1$ thành số nguyên: $k_1′ = \lceil k_1 \rceil$
- Làm tròn xuống $k_2$ thành số nguyên: $k_2′ = \lfloor k_2 \rfloor$
Bước 3: Đếm số vân sáng: $$N_s = k_2′ – k_1′ + 1$$
Ví dụ: Đếm số vân sáng từ $x_1 = 1.5$ mm đến $x_2 = 5.7$ mm, biết $i = 1.2$ mm.
$$k_1 = \frac{1.5}{1.2} = 1.25 \rightarrow k_1′ = 2$$ $$k_2 = \frac{5.7}{1.2} = 4.75 \rightarrow k_2′ = 4$$
$$N_s = 4 – 2 + 1 = 3 \text{ vân sáng}$$
Các vân sáng đó là: bậc 2 ($x = 2.4$ mm), bậc 3 ($x = 3.6$ mm), bậc 4 ($x = 4.8$ mm).
4. Số vân với ánh sáng trắng
Khi dùng ánh sáng trắng, mỗi màu tạo một hệ vân riêng. Vấn đề: Các vân sáng của các màu khác nhau có thể trùng nhau.
Điều kiện vân sáng trùng nhau:
$$k_1\lambda_1 = k_2\lambda_2$$
$$\frac{k_1}{k_2} = \frac{\lambda_2}{\lambda_1}$$
Ví dụ: Ánh sáng đỏ ($\lambda_đ = 750$ nm) và tím ($\lambda_t = 500$ nm)
$$\frac{k_{đỏ}}{k_{tím}} = \frac{500}{750} = \frac{2}{3}$$
Vân đỏ bậc 2 trùng với vân tím bậc 3.
Số vân sáng quan sát được:
Trong khoảng mà vân đỏ bậc $n$ trùng vân tím bậc $m$: $$n = \left\lfloor\frac{\lambda_{đỏ}}{\lambda_{tím}}\right\rfloor \times k$$
V. TRƯỜNG HỢP ĐẶC BIỆT VÀ BÀI TOÁN NÂNG CAO
1. Thay đổi môi trường
Khi nhúng toàn bộ thí nghiệm vào môi trường có chiết suất $n$:
Bước sóng ánh sáng trong môi trường: $$\lambda’ = \frac{\lambda}{n}$$
Khoảng vân mới: $$\boxed{i’ = \frac{\lambda’ D}{a} = \frac{\lambda D}{na} = \frac{i}{n}}$$
Kết luận: Khoảng vân giảm $n$ lần.
Ví dụ: Trong không khí $i = 1.2$ mm. Nhúng vào nước ($n = \frac{4}{3}$), tính $i’$?
$$i’ = \frac{i}{n} = \frac{1.2}{4/3} = 1.2 \times \frac{3}{4} = 0.9 \text{ mm}$$
2. Di chuyển màn hoặc khe
Khi thay đổi khoảng cách D:
$$\boxed{\frac{i_1}{i_2} = \frac{D_1}{D_2}}$$
Khoảng vân tỉ lệ thuận với khoảng cách D.
Khi thay đổi khoảng cách hai khe a:
$$\boxed{\frac{i_1}{i_2} = \frac{a_2}{a_1}}$$
Khoảng vân tỉ lệ nghịch với khoảng cách a.
Ví dụ: Ban đầu $D_1 = 1$ m, $i_1 = 1$ mm. Dời màn ra $D_2 = 2$ m, tính $i_2$?
$$i_2 = i_1 \times \frac{D_2}{D_1} = 1 \times \frac{2}{1} = 2 \text{ mm}$$
3. Đặt tấm mỏng trước một khe
Đặt tấm mỏng trong suốt dày $e$, chiết suất $n$ trước khe S₁:
Quang lộ từ S₁ tăng thêm $(n-1)e$.
Vân trung tâm dịch chuyển:
$$\boxed{x_0 = \frac{D(n-1)e}{a}}$$
Hướng dịch chuyển: Về phía khe có tấm mỏng.
Số vân dịch chuyển:
$$\boxed{\Delta k = \frac{(n-1)e}{\lambda}}$$
Ví dụ: Đặt tấm thủy tinh ($n = 1.5$) dày $e = 10$ μm trước S₁, $\lambda = 600$ nm. Tính số vân dịch chuyển?
$$\Delta k = \frac{(1.5 – 1) \times 10 \times 10^{-6}}{600 \times 10^{-9}} = \frac{0.5 \times 10^{-5}}{6 \times 10^{-7}} = \frac{5}{6} \approx 8.33$$
Dịch chuyển khoảng 8 vân.
4. Vân trùng nhau (hai bước sóng)
Hai nguồn phát đồng thời hai bước sóng $\lambda_1$ và $\lambda_2$:
Điều kiện vân sáng trùng nhau:
$$k_1\lambda_1 = k_2\lambda_2$$
$$\boxed{\frac{k_1}{k_2} = \frac{\lambda_2}{\lambda_1}}$$
Ví dụ: $\lambda_1 = 600$ nm (đỏ), $\lambda_2 = 400$ nm (tím)
$$\frac{k_1}{k_2} = \frac{400}{600} = \frac{2}{3}$$
Vân đỏ bậc 2 trùng vân tím bậc 3.
Vị trí trùng đầu tiên: $$x = 2i_1 = 3i_2$$
VI. BẢNG CÔNG THỨC TỔNG HỢP
A. Khoảng vân
| Đại lượng | Công thức | Đơn vị |
|---|---|---|
| Khoảng vân | $i = \frac{\lambda D}{a}$ | m, mm |
| Bước sóng | $\lambda = \frac{ia}{D}$ | m, nm |
| Khoảng cách hai khe | $a = \frac{\lambda D}{i}$ | m, mm |
| Khoảng cách đến màn | $D = \frac{ia}{\lambda}$ | m |
B. Vị trí vân
| Loại vân | Điều kiện | Vị trí |
|---|---|---|
| Vân sáng | $\delta = k\lambda$ | $x_s = ki$ |
| Vân tối | $\delta = (k+0.5)\lambda$ | $x_t = (k+0.5)i$ |
| Hiệu đường đi | – | $\delta = \frac{ax}{D}$ |
Lưu ý: k là số nguyên ($k \in \mathbb{Z}$): $k = 0, \pm1, \pm2, …$
C. Đếm số vân
| Số vân | Công thức |
|---|---|
| Vân sáng | $N_s = 2\left\lfloor\frac{L}{2i}\right\rfloor + 1$ |
| Vân tối | $N_t = 2\left\lfloor\frac{L}{2i} + 0.5\right\rfloor$ |
D. Trường hợp đặc biệt
| Trường hợp | Công thức |
|---|---|
| Trong môi trường n | $i’ = \frac{i}{n}$ |
| Tỉ lệ khoảng vân | $\frac{i_1}{i_2} = \frac{\lambda_1}{\lambda_2} = \frac{D_1}{D_2} = \frac{a_2}{a_1}$ |
| Tấm mỏng, dịch vân | $\Delta k = \frac{(n-1)e}{\lambda}$ |
| Vân trùng | $\frac{k_1}{k_2} = \frac{\lambda_2}{\lambda_1}$ |
VII. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Khoảng vân:
“Lambda D chia a”
$$i = \frac{\lambda D}{a}$$
Cách nhớ:
- Lambda ở tử
- D ở tử
- a ở mẫu
Vân sáng và vân tối:
“Vân sáng k nguyên, vân tối k rưỡi”
- Vân sáng: $x = ki$ (k nguyên)
- Vân tối: $x = (k + 0.5)i$ (k nửa nguyên)
Đếm số vân:
“Vân sáng lẻ, vân tối chẵn”
- $N_s = 2k_{max} + 1$ (số lẻ)
- $N_t = 2k’_{max}$ (số chẵn)
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm đơn vị
SAI: 600 nm = $6 \times 10^{-6}$ m ❌
ĐÚNG: 600 nm = $6 \times 10^{-7}$ m ✓
Nhớ: 1 nm = $10^{-9}$ m
❌ SAI LẦM 2: Quên đổi đơn vị
SAI: $\lambda = 600$ nm, $a = 1$ mm, thay trực tiếp: $$i = \frac{600 \times D}{1}$$ ❌
ĐÚNG: Đổi hết về mét trước: $$\lambda = 6 \times 10^{-7} \text{ m}, \quad a = 10^{-3} \text{ m}$$ $$i = \frac{6 \times 10^{-7} \times D}{10^{-3}}$$ ✓
❌ SAI LẦM 3: Nhầm công thức vân tối
SAI: Vân tối: $x_t = ki$ ❌
ĐÚNG: Vân tối: $x_t = (k + 0.5)i$ ✓
❌ SAI LẦM 4: Đếm sai số vân
SAI: Đếm số vân sáng: $N_s = \frac{L}{i}$ ❌
ĐÚNG: $N_s = 2\left\lfloor\frac{L}{2i}\right\rfloor + 1$ ✓
Phải tính $k_{max}$ trước, không chia trực tiếp.
❌ SAI LẦM 5: Nhầm $\frac{L}{i}$ với $\frac{L}{2i}$
Phải dùng $\frac{L}{2i}$ vì màn rộng L, nhưng mỗi bên chỉ rộng $\frac{L}{2}$.
3. Kiểm tra kết quả
Kiểm tra 1: Khoảng vân thường cỡ mm
Nếu tính ra $i$ quá lớn (vài cm) hoặc quá nhỏ (vài μm), có thể sai đơn vị.
Kiểm tra 2: Số vân sáng là số lẻ
$$N_s = 1, 3, 5, 7, 9, 11, …$$
Nếu ra số chẵn → sai!
Kiểm tra 3: Số vân tối là số chẵn
$$N_t = 0, 2, 4, 6, 8, 10, …$$
Kiểm tra 4: Vị trí vân đối xứng qua O
Vân sáng bậc k: có 2 vân tại $x = \pm ki$
4. Bảng giá trị bước sóng tham khảo
| Màu sắc | Bước sóng (nm) | Ghi chú |
|---|---|---|
| Đỏ | 620 – 750 | Khoảng vân lớn nhất |
| Cam | 590 – 620 | |
| Vàng | 570 – 590 | |
| Lục | 500 – 570 | Giữa quang phổ |
| Lam | 450 – 500 | |
| Chàm | 430 – 450 | |
| Tím | 380 – 430 | Khoảng vân nhỏ nhất |
Ánh sáng trắng: Hỗn hợp từ 380 nm đến 760 nm
Ghi nhớ thông dụng:
- Đỏ: ~650-700 nm
- Vàng: ~580-600 nm
- Lục: ~520-550 nm
- Lam/Tím: ~450-480 nm
VIII. BÀI TẬP MẪU
Bài 1: Tính khoảng vân
Đề bài: Trong thí nghiệm Young, sử dụng ánh sáng đơn sắc có bước sóng $\lambda = 500$ nm. Khoảng cách hai khe $a = 0.5$ mm, khoảng cách từ hai khe đến màn $D = 1$ m. Tính khoảng vân?
Lời giải:
Bước 1: Đổi đơn vị
- $\lambda = 500$ nm = $500 \times 10^{-9}$ m = $5 \times 10^{-7}$ m
- $a = 0.5$ mm = $0.5 \times 10^{-3}$ m = $5 \times 10^{-4}$ m
- $D = 1$ m
Bước 2: Áp dụng công thức $$i = \frac{\lambda D}{a} = \frac{5 \times 10^{-7} \times 1}{5 \times 10^{-4}}$$
Bước 3: Tính toán $$i = \frac{5 \times 10^{-7}}{5 \times 10^{-4}} = 10^{-3} \text{ m} = 1 \text{ mm}$$
Kết luận: Khoảng vân là 1 mm.
Bài 2: Vị trí vân sáng
Đề bài: Với khoảng vân $i = 1.2$ mm, tính vị trí các vân sáng bậc 3?
Lời giải:
Áp dụng công thức vị trí vân sáng: $$x_s = ki$$
Với k = 3: $$x_3 = 3 \times 1.2 = 3.6 \text{ mm}$$
Kết luận: Có hai vân sáng bậc 3:
- Vân sáng bậc 3 bên phải: $x = +3.6$ mm
- Vân sáng bậc 3 bên trái: $x = -3.6$ mm
Bài 3: Đếm số vân
Đề bài: Màn quan sát có độ rộng 15 mm (đối xứng qua vân trung tâm). Khoảng vân $i = 1.5$ mm. Đếm số vân sáng và vân tối quan sát được trên màn?
Lời giải:
Số vân sáng:
$$k_{max} = \left\lfloor\frac{L}{2i}\right\rfloor = \left\lfloor\frac{15}{2 \times 1.5}\right\rfloor = \left\lfloor\frac{15}{3}\right\rfloor = \left\lfloor 5 \right\rfloor = 5$$
$$N_s = 2k_{max} + 1 = 2 \times 5 + 1 = 11 \text{ vân sáng}$$
Số vân tối:
$$k’_{max} = \left\lfloor\frac{15}{3} + 0.5\right\rfloor = \left\lfloor 5.5 \right\rfloor = 5$$
$$N_t = 2k’_{max} = 2 \times 5 = 10 \text{ vân tối}$$
Kết luận: Có 11 vân sáng và 10 vân tối.
Bài 4: Xác định loại vân
Đề bài: Tại vị trí $x = 4.5$ mm trên màn, khoảng vân $i = 1.5$ mm. Đây là vân gì, bậc mấy?
Lời giải:
Tính bậc: $$k = \frac{x}{i} = \frac{4.5}{1.5} = 3$$
Vì $k = 3$ là số nguyên → Đây là vân sáng bậc 3.
Kết luận: Tại $x = 4.5$ mm là vân sáng bậc 3.
Bài 5: Tính bước sóng
Đề bài: Trong thí nghiệm Young, khoảng vân đo được $i = 0.6$ mm, khoảng cách hai khe $a = 2$ mm, khoảng cách đến màn $D = 2$ m. Tính bước sóng ánh sáng?
Lời giải:
Áp dụng công thức: $$\lambda = \frac{ia}{D} = \frac{0.6 \times 10^{-3} \times 2 \times 10^{-3}}{2}$$
$$= \frac{1.2 \times 10^{-6}}{2} = 0.6 \times 10^{-6} \text{ m} = 6 \times 10^{-7} \text{ m}$$
$$= 600 \text{ nm}$$
Kết luận: Bước sóng ánh sáng là 600 nm (ánh sáng đỏ – cam).
Bài 6: Vân trùng nhau
Đề bài: Chiếu đồng thời hai ánh sáng đơn sắc có bước sóng $\lambda_1 = 720$ nm (đỏ) và $\lambda_2 = 400$ nm (tím) vào thí nghiệm Young. Tính vị trí trùng nhau đầu tiên của hai vân sáng (ngoài vân trung tâm), biết khoảng vân của ánh sáng đỏ là $i_1 = 1.44$ mm.
Lời giải:
Bước 1: Điều kiện vân trùng: $$k_1\lambda_1 = k_2\lambda_2$$
$$\frac{k_1}{k_2} = \frac{\lambda_2}{\lambda_1} = \frac{400}{720} = \frac{5}{9}$$
Bước 2: Vân trùng đầu tiên (ngoài vân trung tâm):
- $k_1 = 5$ (vân đỏ bậc 5)
- $k_2 = 9$ (vân tím bậc 9)
Bước 3: Vị trí trùng: $$x = k_1 i_1 = 5 \times 1.44 = 7.2 \text{ mm}$$
Kiểm tra:
- Khoảng vân tím: $i_2 = \frac{\lambda_2}{\lambda_1} \times i_1 = \frac{400}{720} \times 1.44 = 0.8$ mm
- Vị trí vân tím bậc 9: $x = 9 \times 0.8 = 7.2$ mm ✓
Kết luận: Vị trí trùng đầu tiên (ngoài vân trung tâm) là $x = \pm 7.2$ mm.
Bài 7: Môi trường chiết suất
Đề bài: Trong không khí, khoảng vân đo được $i = 1.2$ mm. Nếu nhúng toàn bộ thí nghiệm vào nước có chiết suất $n = \frac{4}{3}$, tính khoảng vân mới?
Lời giải:
Áp dụng công thức: $$i’ = \frac{i}{n} = \frac{1.2}{4/3} = 1.2 \times \frac{3}{4} = 0.9 \text{ mm}$$
Kết luận: Khoảng vân trong nước là 0.9 mm.
IX. KẾT LUẬN
Bài viết đã trình bày hệ thống đầy đủ các công thức giao thoa ánh sáng:
Khoảng vân:
- Công thức cơ bản: $i = \frac{\lambda D}{a}$
- Tỉ lệ: $\frac{i_1}{i_2} = \frac{\lambda_1}{\lambda_2}$
Vị trí vân:
- Vân sáng: $x_s = ki$ (k nguyên)
- Vân tối: $x_t = (k + 0.5)i$ (k nửa nguyên)
- Hiệu đường đi: $\delta = \frac{ax}{D}$
Đếm số vân:
- Vân sáng: $N_s = 2k_{max} + 1$ (số lẻ)
- Vân tối: $N_t = 2k’_{max}$ (số chẵn)
Trường hợp đặc biệt:
- Môi trường: $i’ = \frac{i}{n}$
- Vân trùng: $\frac{k_1}{k_2} = \frac{\lambda_2}{\lambda_1}$
7 bài tập mẫu có lời giải từng bước chi tiết
Công thức QUAN TRỌNG NHẤT
🔥 Top 3 công thức cần nhớ:
1. Khoảng vân: $$\boxed{i = \frac{\lambda D}{a}}$$
2. Vị trí vân sáng: $$\boxed{x_s = ki \quad (k \in \mathbb{Z})}$$
3. Vị trí vân tối: $$\boxed{x_t = (k + 0.5)i \quad (k \in \mathbb{Z})}$$
Từ công thức khoảng vân, suy ra:
- Vị trí vân: $x = ki$ (vân sáng)
- Số vân: $N_s = 2\left\lfloor\frac{L}{2i}\right\rfloor + 1$
- Tỉ lệ: Khoảng vân tỉ lệ thuận với λ, D; tỉ lệ nghịch với a

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
