Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ THẤU KÍNH
- 1. Thấu kính là gì?
- 2. So sánh hai loại thấu kính
- 3. Các khái niệm cơ bản
- II. CÔNG THỨC CƠ BẢN CỦA THẤU KÍNH
- 1. Công thức thấu kính (Công thức chính)
- 2. Quy ước dấu
- 3. Công thức độ phóng đại
- 4. Công thức độ tụ
- 5. Ví dụ minh họa chi tiết
- III. THẤU KÍNH HỘI TỤ
- 1. Đặc điểm thấu kính hội tụ
- 2. Công thức cho thấu kính hội tụ
- 3. Các trường hợp tạo ảnh
- 4. Bảng tóm tắt chi tiết
- 5. Ví dụ thấu kính hội tụ
- IV. THẤU KÍNH PHÂN KÌ
- 1. Đặc điểm thấu kính phân kì
- 2. Công thức cho thấu kính phân kì
- 3. Tính chất ảnh của TKPK
- 4. Công thức đơn giản hóa cho TKPK
- 5. Ứng dụng thấu kính phân kì
- 6. Ví dụ thấu kính phân kì
- V. CÔNG THỨC BỔ SUNG VÀ ĐẶC BIỆT
- 1. Công thức Newton
- 2. Công thức nhà máy thấu kính
- 3. Ghép thấu kính sát nhau
- 4. Công thức kính lúp
- VI. BẢNG CÔNG THỨC TỔNG HỢP
- A. Công thức cơ bản
- B. Quy ước dấu
- C. Phân loại thấu kính
- D. Công thức đặc biệt
- VII. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Kiểm tra kết quả
- 4. Bảng tham khảo ứng dụng
- VIII. BÀI TẬP MẪU
- IX. KẾT LUẬN
- Công thức QUAN TRỌNG NHẤT
I. GIỚI THIỆU VỀ THẤU KÍNH
1. Thấu kính là gì?
Định nghĩa: Thấu kính là một khối chất trong suốt (thường làm bằng thủy tinh hoặc nhựa trong), được giới hạn bởi hai mặt cong (hoặc một mặt cong và một mặt phẳng). Thấu kính có khả năng làm thay đổi phương truyền của các tia sáng qua nó.
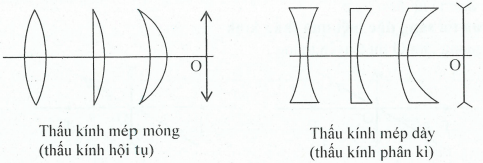
Cấu tạo:
- Được làm từ vật liệu trong suốt: thủy tinh, nhựa, pha lê
- Có hai mặt: có thể là mặt cầu lồi, mặt cầu lõm, hoặc mặt phẳng
- Chiết suất của thấu kính lớn hơn chiết suất môi trường xung quanh
Phân loại: Có hai loại thấu kính chính:
- Thấu kính hội tụ (TKHT): Còn gọi là thấu kính lồi
- Thấu kính phân kì (TKPK): Còn gọi là thấu kính lõm
2. So sánh hai loại thấu kính
| Tiêu chí | Thấu kính hội tụ | Thấu kính phân kì |
|---|---|---|
| Hình dạng | Giữa dày, rìa mỏng | Giữa mỏng, rìa dày |
| Ký hiệu vẽ | ⟨ ⟩ hoặc ⟨│⟩ | ) ( hoặc │(│ |
| Tiêu cự f | f > 0 (dương) | f < 0 (âm) |
| Độ tụ D | D > 0 (dương) | D < 0 (âm) |
| Tác dụng | Hội tụ chùm tia song song | Làm phân kì chùm tia song song |
| Ảnh tạo ra | Ảnh thật hoặc ảnh ảo | Luôn cho ảnh ảo |
| Ví dụ ứng dụng | Kính lúp, máy ảnh, mắt | Kính cận thị |
Cách nhận biết:
- TKHT: Khi nhìn qua thấu kính, chữ to hơn → thấu kính hội tụ
- TKPK: Khi nhìn qua thấu kính, chữ nhỏ hơn → thấu kính phân kì
3. Các khái niệm cơ bản
| Khái niệm | Ký hiệu | Ý nghĩa |
|---|---|---|
| Trục chính | $\Delta$ | Đường thẳng đi qua tâm quang học và vuông góc với thấu kính |
| Quang tâm | O | Điểm nằm ở trung tâm của thấu kính, tia sáng qua O không đổi hướng |
| Tiêu điểm vật | F | Điểm trên trục chính, nếu vật đặt tại F thì ảnh ở vô cực |
| Tiêu điểm ảnh | F’ | Điểm hội tụ (TKHT) hoặc dường như phát ra (TKPK) của chùm tia song song với trục chính |
| Tiêu cự | f | Khoảng cách từ quang tâm O đến tiêu điểm: OF = OF’ = f |
| Tiêu diện | (P), (P’) | Mặt phẳng đi qua tiêu điểm và vuông góc với trục chính |
Tính chất quan trọng:
- Tia sáng qua quang tâm O không đổi hướng
- Chùm tia song song với trục chính sau khi qua TKHT hội tụ tại F’, qua TKPK dường như phát ra từ F
- Với thấu kính mỏng: OF = OF’ = |f|
II. CÔNG THỨC CƠ BẢN CỦA THẤU KÍNH
1. Công thức thấu kính (Công thức chính)
📌 Công thức QUAN TRỌNG NHẤT trong chương thấu kính:
$$\boxed{\frac{1}{f} = \frac{1}{d} + \frac{1}{d’}}$$
Hoặc có thể viết dưới dạng:
$$\frac{1}{d’} = \frac{1}{f} – \frac{1}{d}$$
Trong đó:
- $f$: tiêu cự của thấu kính (m, cm)
- $d$: khoảng cách từ vật đến thấu kính (m, cm)
- $d’$: khoảng cách từ ảnh đến thấu kính (m, cm)
Ý nghĩa: Công thức này cho phép tính vị trí ảnh khi biết vị trí vật và tiêu cự, hoặc ngược lại.
Điều kiện áp dụng:
- Thấu kính mỏng (bề dày không đáng kể)
- Vật đặt gần trục chính
- Góc tới nhỏ
Nguồn gốc: Công thức xuất phát từ định luật khúc xạ ánh sáng qua hai mặt cong của thấu kính.
2. Quy ước dấu
Quy ước dấu rất quan trọng để áp dụng đúng công thức:
| Đại lượng | Dấu dương (+) | Dấu âm (-) |
|---|---|---|
| Tiêu cự f | Thấu kính hội tụ | Thấu kính phân kì |
| Khoảng cách vật d | Vật thật (luôn dương trong trường hợp cơ bản) | Vật ảo (hiếm gặp) |
| Khoảng cách ảnh d’ | Ảnh thật (cùng phía với ảnh thật so với TK) | Ảnh ảo (cùng phía với vật) |
| Độ phóng đại k | Ảnh cùng chiều với vật | Ảnh ngược chiều với vật |
Giải thích chi tiết:
Tiêu cự f:
- TKHT: $f > 0$ (tiêu điểm F’ nằm phía sau thấu kính)
- TKPK: $f < 0$ (tiêu điểm F’ nằm phía trước thấu kính)
Khoảng cách vật d:
- Vật thật: $d > 0$ (vật đặt trước thấu kính) – trường hợp thông thường
- Trong các bài toán cơ bản, d luôn dương
Khoảng cách ảnh d’:
- Ảnh thật: $d’ > 0$ (ảnh hứng được trên màn, ở phía sau thấu kính)
- Ảnh ảo: $d’ < 0$ (ảnh không hứng được trên màn, ở phía trước thấu kính, cùng phía với vật)
Lưu ý quan trọng:
- Vật thật: $d > 0$ (luôn đúng trong trường hợp cơ bản)
- TKHT: $f > 0$, có thể cho ảnh thật ($d’ > 0$) hoặc ảnh ảo ($d’ < 0$) tùy vào vị trí vật
- TKPK: $f < 0$, luôn luôn cho ảnh ảo ($d’ < 0$) với mọi vị trí vật
3. Công thức độ phóng đại
Độ phóng đại ảnh là tỉ số giữa chiều cao của ảnh và chiều cao của vật:
$$\boxed{k = \frac{h’}{h} = -\frac{d’}{d}}$$
Trong đó:
- $k$: độ phóng đại (không có đơn vị)
- $h$: chiều cao của vật (cm, m)
- $h’$: chiều cao của ảnh (cm, m)
- $d$: khoảng cách từ vật đến thấu kính
- $d’$: khoảng cách từ ảnh đến thấu kính
Ý nghĩa của độ phóng đại:
Độ lớn của k:
- $|k| > 1$: ảnh lớn hơn vật (ảnh được phóng to)
- $|k| = 1$: ảnh bằng vật
- $|k| < 1$: ảnh nhỏ hơn vật (ảnh bị thu nhỏ)
Dấu của k:
- $k > 0$: ảnh cùng chiều với vật → ảnh ảo
- $k < 0$: ảnh ngược chiều với vật → ảnh thật
Lưu ý: Dấu âm trong công thức $k = -\frac{d’}{d}$ rất quan trọng, không được bỏ qua!
4. Công thức độ tụ
Độ tụ là đại lượng đặc trưng cho khả năng hội tụ hoặc phân kì ánh sáng của thấu kính:
$$\boxed{D = \frac{1}{f}}$$
Đơn vị:
- Khi $f$ đo bằng mét (m) → $D$ đo bằng điốp (dp) hoặc diôptơ (D)
- 1 điốp = 1 m⁻¹
Ví dụ:
- $f = 0.5$ m = 50 cm → $D = \frac{1}{0.5} = 2$ dp
- $f = -25$ cm = -0.25 m → $D = \frac{1}{-0.25} = -4$ dp
- $f = 20$ cm = 0.2 m → $D = \frac{1}{0.2} = 5$ dp
Ý nghĩa:
- $D > 0$: thấu kính hội tụ (khả năng hội tụ tia sáng)
- $D < 0$: thấu kính phân kì (làm tia sáng phân kì)
- $|D|$ càng lớn: khả năng hội tụ/phân kì càng mạnh (tiêu cự càng ngắn)
Lưu ý quan trọng: Khi tính độ tụ, bắt buộc phải đổi tiêu cự về đơn vị mét.
5. Ví dụ minh họa chi tiết
Bài toán: Một vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ có tiêu cự 20 cm, cách thấu kính 30 cm.
a) Xác định vị trí, tính chất của ảnh b) Tính độ phóng đại và chiều cao ảnh nếu vật cao 5 cm
Lời giải:
a) Tìm vị trí và tính chất ảnh:
Cho biết:
- $f = 20$ cm (TKHT vì f > 0)
- $d = 30$ cm
Áp dụng công thức thấu kính: $$\frac{1}{d’} = \frac{1}{f} – \frac{1}{d} = \frac{1}{20} – \frac{1}{30}$$
$$= \frac{3 – 2}{60} = \frac{1}{60}$$
$$d’ = 60 \text{ cm}$$
Kết luận:
- Vì $d’ = 60$ cm $> 0$ → Ảnh thật
- Ảnh cách thấu kính 60 cm, ở phía đối diện với vật
b) Tính độ phóng đại và chiều cao ảnh:
$$k = -\frac{d’}{d} = -\frac{60}{30} = -2$$
Ý nghĩa:
- $|k| = 2 > 1$: ảnh lớn gấp 2 lần vật
- $k < 0$: ảnh ngược chiều với vật (xác nhận ảnh thật)
Chiều cao ảnh: $$h’ = k \times h = -2 \times 5 = -10 \text{ cm}$$
Dấu âm cho biết ảnh ngược chiều.
Kết luận cuối cùng: Ảnh thật, ngược chiều, cao 10 cm, cách thấu kính 60 cm, lớn gấp 2 lần vật.
III. THẤU KÍNH HỘI TỤ
1. Đặc điểm thấu kính hội tụ
Hình dạng:
- Phần giữa dày hơn phần rìa
- Có dạng lồi ở giữa
- Thường gọi là thấu kính lồi
Tính chất quang học:
- Tiêu cự: $f > 0$ (dương)
- Độ tụ: $D > 0$ (dương)
- Ký hiệu: ⟨ ⟩ hoặc ⟨│⟩
Tác dụng:
- Làm hội tụ (tụ lại) chùm tia sáng song song với trục chính
- Chùm tia sau khi qua thấu kính hội tụ tại tiêu điểm F’ (phía sau thấu kính)
2. Công thức cho thấu kính hội tụ
Công thức thấu kính: $$\boxed{\frac{1}{f} = \frac{1}{d} + \frac{1}{d’} \quad \text{với } f > 0}$$
Độ tụ: $$\boxed{D = \frac{1}{f} \quad \text{với } D > 0}$$
Độ phóng đại: $$k = -\frac{d’}{d}$$
3. Các trường hợp tạo ảnh
Tính chất ảnh phụ thuộc vào vị trí vật so với tiêu điểm:
a) Vật ở rất xa (d → ∞):
- Ảnh tạo tại tiêu điểm ảnh F’: $d’ = f$
- Ảnh thật, rất nhỏ, ngược chiều
- Ứng dụng: Thu được ảnh của mặt trời, các ngôi sao
b) Vật ở ngoài khoảng tiêu cự (d > f):
- $d’ > 0$ → Ảnh thật, ngược chiều với vật
- Có thể nhỏ hơn, bằng hoặc lớn hơn vật tùy vào vị trí cụ thể
- Ứng dụng: Máy ảnh, máy chiếu, mắt người
Chia nhỏ:
- d > 2f: Ảnh thật, ngược chiều, nhỏ hơn vật ($f < d’ < 2f$)
- d = 2f: Ảnh thật, ngược chiều, bằng vật ($d’ = 2f$)
- f < d < 2f: Ảnh thật, ngược chiều, lớn hơn vật ($d’ > 2f$)
c) Vật tại tiêu điểm F (d = f):
- $d’ \to \infty$ → Không tạo ảnh (ảnh ở vô cực)
- Các tia ló ra song song với nhau
- Ứng dụng: Đèn pha, đèn pin (đặt bóng đèn tại tiêu điểm)
d) Vật trong khoảng tiêu cự (d < f):
- $d’ < 0$ → Ảnh ảo, cùng chiều với vật, lớn hơn vật
- $k > 0$, $|k| > 1$
- Ứng dụng: Kính lúp để quan sát vật nhỏ
4. Bảng tóm tắt chi tiết
| Vị trí vật | Khoảng cách d | Khoảng cách ảnh d’ | Tính chất ảnh | Độ phóng đại k |
|---|---|---|---|---|
| Rất xa | $d \to \infty$ | $d’ = f$ | Thật, rất nhỏ, tại F’ | $k \to 0$ |
| Xa (d > 2f) | $d > 2f$ | $f < d’ < 2f$ | Thật, ngược chiều, nhỏ hơn vật | $-1 < k < 0$ |
| Tại 2f | $d = 2f$ | $d’ = 2f$ | Thật, ngược chiều, bằng vật | $k = -1$ |
| Giữa f và 2f | $f < d < 2f$ | $d’ > 2f$ | Thật, ngược chiều, lớn hơn vật | $k < -1$ |
| Tại F | $d = f$ | $d’ \to \infty$ | Không có ảnh | Không xác định |
| Trong tiêu cự | $d < f$ | $d’ < 0$ | Ảo, cùng chiều, lớn hơn vật | $k > 1$ |
5. Ví dụ thấu kính hội tụ
Bài toán: Một thấu kính hội tụ có tiêu cự f = 15 cm. Đặt vật AB vuông góc với trục chính, cách thấu kính 10 cm, cao 4 cm. Xác định ảnh và vẽ ảnh.
Lời giải:
Nhận xét: $d = 10$ cm $< f = 15$ cm → Vật trong khoảng tiêu cự → Ảnh ảo
Tính toán: $$\frac{1}{d’} = \frac{1}{f} – \frac{1}{d} = \frac{1}{15} – \frac{1}{10}$$
$$= \frac{2 – 3}{30} = -\frac{1}{30}$$
$$d’ = -30 \text{ cm}$$
Tính chất:
- $d’ < 0$ → Ảnh ảo
- Ảnh cách thấu kính 30 cm, cùng phía với vật
Độ phóng đại: $$k = -\frac{d’}{d} = -\frac{-30}{10} = 3$$
- $k = 3 > 0$ → Ảnh cùng chiều với vật (xác nhận ảnh ảo)
- $|k| = 3 > 1$ → Ảnh lớn gấp 3 lần vật
Chiều cao ảnh: $$h’ = k \times h = 3 \times 4 = 12 \text{ cm}$$
Kết luận: Ảnh ảo A’B’, cùng chiều, cao 12 cm, cách thấu kính 30 cm về phía vật (cùng phía với AB).
IV. THẤU KÍNH PHÂN KÌ
1. Đặc điểm thấu kính phân kì
Hình dạng:
- Phần giữa mỏng hơn phần rìa
- Có dạng lõm ở giữa
- Thường gọi là thấu kính lõm
Tính chất quang học:
- Tiêu cự: $f < 0$ (âm)
- Độ tụ: $D < 0$ (âm)
- Ký hiệu: ) ( hoặc │(│
Tác dụng:
- Làm phân kì (tản ra) chùm tia sáng song song với trục chính
- Chùm tia sau khi qua thấu kính có đường kéo dài hội tụ tại tiêu điểm F (phía trước thấu kính)
2. Công thức cho thấu kính phân kì
Công thức thấu kính: $$\boxed{\frac{1}{f} = \frac{1}{d} + \frac{1}{d’} \quad \text{với } f < 0}$$
Độ tụ: $$\boxed{D = \frac{1}{f} \quad \text{với } D < 0}$$
Độ phóng đại: $$k = -\frac{d’}{d}$$
3. Tính chất ảnh của TKPK
Điều quan trọng: Thấu kính phân kì LUÔN LUÔN cho:
- Ảnh ảo ($d’ < 0$) với mọi vị trí vật
- Ảnh cùng chiều với vật ($k > 0$)
- Ảnh nhỏ hơn vật ($0 < |k| < 1$)
Không phụ thuộc vào vị trí đặt vật, ảnh luôn có tính chất như trên.
Vị trí ảnh:
- Ảnh ảo nằm cùng phía với vật, gần thấu kính hơn vật
- Ảnh nằm trong khoảng từ quang tâm O đến tiêu điểm F
4. Công thức đơn giản hóa cho TKPK
Với $f < 0$, $d > 0$, có thể viết:
$$|d’| = \frac{|f| \cdot d}{d + |f|}$$
Chứng minh: $$\frac{1}{d’} = \frac{1}{f} – \frac{1}{d} = -\frac{1}{|f|} – \frac{1}{d} = -\frac{d + |f|}{|f| \cdot d}$$
$$d’ = -\frac{|f| \cdot d}{d + |f|}$$
Lấy trị tuyệt đối: $|d’| = \frac{|f| \cdot d}{d + |f|}$
Ví dụ: $f = -20$ cm, $d = 30$ cm
$$|d’| = \frac{20 \times 30}{30 + 20} = \frac{600}{50} = 12 \text{ cm}$$
→ $d’ = -12$ cm (ảnh ảo)
5. Ứng dụng thấu kính phân kì
Kính cận thị:
- Người cận thị có tiêu điểm ảnh của mắt nằm trước võng mạc
- Dùng TKPK để làm chùm sáng phân kì trước khi vào mắt
- Giúp ảnh rõ nét trên võng mạc
Kính thiên văn:
- Thấu kính mắt của kính thiên văn thường là TKPK
- Kết hợp với vật kính (TKHT) để quan sát thiên thể
Cửa sổ quan sát (mắt cá):
- Mở rộng tầm nhìn
- Quan sát phạm vi rộng hơn
Kính chiếu hậu xe:
- Mở rộng trường nhìn
- Giúp quan sát phía sau rộng hơn
6. Ví dụ thấu kính phân kì
Bài toán: Một thấu kính phân kì có tiêu cự $f = -15$ cm. Đặt vật AB cao 4 cm vuông góc với trục chính, cách thấu kính 20 cm. Xác định vị trí, tính chất và chiều cao ảnh.
Lời giải:
Cho biết:
- $f = -15$ cm (TKPK)
- $d = 20$ cm
- $h = 4$ cm
Tính vị trí ảnh: $$\frac{1}{d’} = \frac{1}{f} – \frac{1}{d} = \frac{1}{-15} – \frac{1}{20}$$
$$= -\frac{1}{15} – \frac{1}{20} = -\frac{4 + 3}{60} = -\frac{7}{60}$$
$$d’ = -\frac{60}{7} \approx -8.57 \text{ cm}$$
Tính chất:
- $d’ < 0$ → Ảnh ảo
- Ảnh cách thấu kính khoảng 8.57 cm, cùng phía với vật
Độ phóng đại: $$k = -\frac{d’}{d} = -\frac{-60/7}{20} = \frac{60}{140} = \frac{3}{7} \approx 0.43$$
- $k > 0$ → Ảnh cùng chiều với vật
- $0 < k < 1$ → Ảnh nhỏ hơn vật
Chiều cao ảnh: $$h’ = k \times h = \frac{3}{7} \times 4 = \frac{12}{7} \approx 1.71 \text{ cm}$$
Kết luận: Ảnh ảo A’B’, cùng chiều với vật, cao khoảng 1.71 cm (nhỏ hơn vật khoảng 2.3 lần), cách thấu kính 8.57 cm về phía vật.
V. CÔNG THỨC BỔ SUNG VÀ ĐẶC BIỆT
1. Công thức Newton
Khi biết khoảng cách từ vật và ảnh đến tiêu điểm:
$$\boxed{\overline{FA} \cdot \overline{F’A’} = f^2}$$
Hoặc viết:
$$d_1 \cdot d_2 = f^2$$
Trong đó:
- $d_1 = d – f$: khoảng cách từ vật A đến tiêu điểm vật F
- $d_2 = d’ – f$: khoảng cách từ ảnh A’ đến tiêu điểm ảnh F’
- $f$: tiêu cự thấu kính
Ưu điểm: Thuận tiện khi biết khoảng cách đến tiêu điểm thay vì khoảng cách đến thấu kính.
Ví dụ: Vật cách tiêu điểm vật F một khoảng 5 cm, thấu kính có f = 10 cm. Tính khoảng cách từ ảnh đến tiêu điểm ảnh F’?
$$d_2 = \frac{f^2}{d_1} = \frac{10^2}{5} = 20 \text{ cm}$$
2. Công thức nhà máy thấu kính
Tính tiêu cự từ chiết suất và bán kính cong:
$$\boxed{\frac{1}{f} = (n – 1)\left(\frac{1}{R_1} – \frac{1}{R_2}\right)}$$
Trong đó:
- $n$: chiết suất của thấu kính (ví dụ: thủy tinh n ≈ 1.5)
- $R_1$: bán kính mặt cong thứ nhất
- $R_2$: bán kính mặt cong thứ hai
Quy ước:
- $R > 0$: mặt lồi (nhìn từ phía ánh sáng tới)
- $R < 0$: mặt lõm
- $R = \infty$: mặt phẳng
Ví dụ: Thấu kính hai mặt lồi bằng thủy tinh ($n = 1.5$), có $R_1 = 20$ cm, $R_2 = -20$ cm (mặt sau lõm). Tính f?
$$\frac{1}{f} = (1.5 – 1)\left(\frac{1}{20} – \frac{1}{-20}\right) = 0.5 \times \frac{2}{20} = \frac{1}{20}$$
$$f = 20 \text{ cm}$$
3. Ghép thấu kính sát nhau
Khi ghép hai thấu kính sát nhau (khoảng cách giữa chúng không đáng kể):
Công thức tiêu cự: $$\boxed{\frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2}}$$
Công thức độ tụ: $$\boxed{D = D_1 + D_2}$$
Trong đó:
- $f$, $D$: tiêu cự và độ tụ của hệ thấu kính
- $f_1$, $D_1$: tiêu cự và độ tụ của thấu kính thứ nhất
- $f_2$, $D_2$: tiêu cự và độ tụ của thấu kính thứ hai
Ví dụ: Ghép TKHT có $f_1 = 20$ cm với TKPK có $f_2 = -30$ cm. Tính tiêu cự và độ tụ của hệ?
Lời giải: $$\frac{1}{f} = \frac{1}{20} + \frac{1}{-30} = \frac{3 – 2}{60} = \frac{1}{60}$$
$$f = 60 \text{ cm} = 0.6 \text{ m}$$
Vì $f > 0$ → Hệ là thấu kính hội tụ
Độ tụ: $$D = \frac{1}{0.6} = \frac{5}{3} \approx 1.67 \text{ dp}$$
Hoặc: $D_1 = 5$ dp, $D_2 = -\frac{10}{3}$ dp
$$D = 5 – \frac{10}{3} = \frac{5}{3} \text{ dp}$$
4. Công thức kính lúp
Độ bội giác (số bội giác) của kính lúp:
$$\boxed{G = \frac{\alpha’}{\alpha_0} = \frac{D_{cc}}{f}}$$
Trong đó:
- $G$: độ bội giác (lần)
- $\alpha’$: góc trông ảnh qua kính lúp
- $\alpha_0$: góc trông vật khi không dùng kính
- $D_{cc} = 25$ cm: khoảng nhìn rõ ngắn nhất (cự ly điểm cực cận)
- $f$: tiêu cự kính lúp (tính bằng cm)
Công thức đơn giản: $$G = \frac{25}{f \text{(cm)}}$$
Ví dụ: Kính lúp có tiêu cự $f = 5$ cm. Tính độ bội giác?
$$G = \frac{25}{5} = 5 \text{ lần}$$
Ảnh qua kính lớn gấp 5 lần so với nhìn trực tiếp.
VI. BẢNG CÔNG THỨC TỔNG HỢP
A. Công thức cơ bản
| Tên công thức | Biểu thức | Ghi chú |
|---|---|---|
| Công thức thấu kính | $\frac{1}{f} = \frac{1}{d} + \frac{1}{d’}$ | Công thức quan trọng nhất |
| Độ phóng đại | $k = \frac{h’}{h} = -\frac{d’}{d}$ | Chú ý dấu âm |
| Độ tụ | $D = \frac{1}{f}$ | f phải tính bằng mét (m) |
B. Quy ước dấu
| Đại lượng | Dương (+) | Âm (-) | Ghi chú |
|---|---|---|---|
| f | Thấu kính hội tụ | Thấu kính phân kì | TKHT: f > 0, TKPK: f < 0 |
| d | Vật thật | Vật ảo | Thường d > 0 |
| d’ | Ảnh thật | Ảnh ảo | d’ > 0: ảnh thật, d’ < 0: ảnh ảo |
| k | Ảnh cùng chiều | Ảnh ngược chiều | k > 0: ảnh ảo, k < 0: ảnh thật |
C. Phân loại thấu kính
| Loại | Tiêu cự f | Độ tụ D | Hình dạng | Ảnh |
|---|---|---|---|---|
| Hội tụ | f > 0 | D > 0 | Giữa dày, rìa mỏng | Thật hoặc ảo |
| Phân kì | f < 0 | D < 0 | Giữa mỏng, rìa dày | Luôn ảo |
D. Công thức đặc biệt
| Trường hợp | Công thức | Điều kiện |
|---|---|---|
| Newton | $d_1 \cdot d_2 = f^2$ | $d_1 = d – f$, $d_2 = d’ – f$ |
| Nhà máy TK | $\frac{1}{f} = (n-1)\left(\frac{1}{R_1} – \frac{1}{R_2}\right)$ | n: chiết suất, R: bán kính |
| Ghép TK | $\frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2}$ | Ghép sát |
| Độ tụ ghép | $D = D_1 + D_2$ | Ghép sát |
| Độ bội giác | $G = \frac{25}{f \text{(cm)}}$ | Kính lúp, $D_{cc} = 25$ cm |
VII. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Công thức thấu kính:
“Một chia f bằng một chia d cộng một chia d'”
$$\frac{1}{f} = \frac{1}{d} + \frac{1}{d’}$$
Cách nhớ: Ba phân số, cộng lại bằng nhau
Độ phóng đại:
“k bằng âm d’ chia d”
$$k = -\frac{d’}{d}$$
Nhớ dấu âm: Rất quan trọng, không được quên!
Nhớ dấu của f:
“Hội tụ → f Dương”
“Phân kì → f Âm”
- TKHT: f > 0 (Dương)
- TKPK: f < 0 (Âm)
Nhớ tính chất ảnh:
“TKPK luôn luôn cho ảnh ảo, cùng chiều, nhỏ hơn”
Không phụ thuộc vị trí vật.
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Quên quy ước dấu của f
SAI: Coi TKPK có f = 20 cm ❌
ĐÚNG: TKPK có f = -20 cm ✓
Nhớ: TKPK luôn có f < 0
❌ SAI LẦM 2: Nhầm ảnh thật và ảnh ảo
SAI: d’ = -30 cm → ảnh thật ❌
ĐÚNG: d’ < 0 → ảnh ảo ✓
Quy tắc:
- d’ > 0: ảnh thật
- d’ < 0: ảnh ảo
❌ SAI LẦM 3: Quên dấu âm trong công thức k
SAI: $k = \frac{d’}{d}$ ❌
ĐÚNG: $k = -\frac{d’}{d}$ ✓
Dấu âm là bắt buộc!
❌ SAI LẦM 4: Nhầm đơn vị khi tính D
SAI: f = 25 cm → D = 1/25 = 0.04 dp ❌
ĐÚNG: f = 0.25 m → D = 1/0.25 = 4 dp ✓
Nhớ: Phải đổi f sang mét (m) trước khi tính D
❌ SAI LẦM 5: Cho rằng TKPK có thể cho ảnh thật
SAI: TKPK với d = 30 cm cho ảnh thật ❌
ĐÚNG: TKPK luôn luôn cho ảnh ảo với mọi d ✓
3. Kiểm tra kết quả
Kiểm tra 1: TKHT với d > f
Nếu $d > f$ (TKHT) → phải có $d’ > 0$ (ảnh thật)
Kiểm tra 2: TKHT với d < f
Nếu $d < f$ (TKHT) → phải có $d’ < 0$ (ảnh ảo)
Kiểm tra 3: TKPK bất kỳ
Với TKPK, luôn luôn $d’ < 0$ (ảnh ảo), $k > 0$ (cùng chiều)
Kiểm tra 4: Ảnh thật và k
Ảnh thật → $k < 0$ (ngược chiều)
Kiểm tra 5: Ảnh ảo và k
Ảnh ảo → $k > 0$ (cùng chiều)
4. Bảng tham khảo ứng dụng
| Ứng dụng | Loại thấu kính | Tiêu cự f (cm) | Ghi chú |
|---|---|---|---|
| Kính lúp | Hội tụ | 5 – 10 | Xem vật nhỏ |
| Máy ảnh | Hội tụ | 5 – 50 | Tạo ảnh thật |
| Kính cận thị | Phân kì | -50 đến -200 | Điều chỉnh cận |
| Kính viễn thị | Hội tụ | 100 – 200 | Điều chỉnh viễn |
| Kính hiển vi (vật kính) | Hội tụ | 0.2 – 2 | Tiêu cự rất ngắn |
| Kính thiên văn | Hội tụ + Phân kì | Vật kính: 50-200 | Quan sát xa |
VIII. BÀI TẬP MẪU
Bài 1: Tính vị trí ảnh (TKHT)
Đề bài: Một thấu kính hội tụ có tiêu cự f = 12 cm. Đặt vật AB vuông góc với trục chính, cách thấu kính 18 cm. Tìm vị trí và tính chất của ảnh?
Lời giải:
Cho biết:
- f = 12 cm (TKHT)
- d = 18 cm
Áp dụng công thức thấu kính: $$\frac{1}{d’} = \frac{1}{f} – \frac{1}{d} = \frac{1}{12} – \frac{1}{18}$$
$$= \frac{3 – 2}{36} = \frac{1}{36}$$
$$d’ = 36 \text{ cm}$$
Kết luận:
- Vì $d’ = 36$ cm $> 0$ → Ảnh thật
- Ảnh cách thấu kính 36 cm, ở phía đối diện với vật
- Vì d > f → ảnh thật (xác nhận đúng)
Bài 2: Tính độ phóng đại và chiều cao ảnh
Đề bài: (Tiếp bài 1) Tính độ phóng đại và chiều cao ảnh nếu vật cao 3 cm?
Lời giải:
Tính độ phóng đại: $$k = -\frac{d’}{d} = -\frac{36}{18} = -2$$
Ý nghĩa:
- $|k| = 2 > 1$: ảnh lớn gấp 2 lần vật
- $k < 0$: ảnh ngược chiều với vật (xác nhận ảnh thật)
Chiều cao ảnh: $$h’ = k \times h = -2 \times 3 = -6 \text{ cm}$$
Dấu âm cho biết ảnh ngược chiều.
Kết luận: Ảnh cao 6 cm, ngược chiều với vật, lớn gấp 2 lần vật.
Bài 3: Tính tiêu cự từ vị trí vật và ảnh
Đề bài: Một vật đặt cách thấu kính 20 cm cho ảnh thật cách thấu kính 60 cm. Tính tiêu cự và xác định loại thấu kính?
Lời giải:
Cho biết:
- d = 20 cm
- d’ = 60 cm > 0 (ảnh thật)
Áp dụng công thức: $$\frac{1}{f} = \frac{1}{d} + \frac{1}{d’} = \frac{1}{20} + \frac{1}{60}$$
$$= \frac{3 + 1}{60} = \frac{4}{60} = \frac{1}{15}$$
$$f = 15 \text{ cm}$$
Kết luận:
- Vì $f = 15$ cm $> 0$ → Thấu kính hội tụ
- Tiêu cự 15 cm
Bài 4: Bài toán TKPK
Đề bài: Một thấu kính phân kì có tiêu cự f = -10 cm. Đặt vật cao 2 cm, cách thấu kính 15 cm. Tìm vị trí, tính chất và chiều cao ảnh?
Lời giải:
Cho biết:
- f = -10 cm (TKPK)
- d = 15 cm
- h = 2 cm
Tính vị trí ảnh: $$\frac{1}{d’} = \frac{1}{f} – \frac{1}{d} = \frac{1}{-10} – \frac{1}{15}$$
$$= -\frac{1}{10} – \frac{1}{15} = -\frac{3 + 2}{30} = -\frac{5}{30} = -\frac{1}{6}$$
$$d’ = -6 \text{ cm}$$
Tính chất: $d’ < 0$ → Ảnh ảo, cách TK 6 cm, cùng phía với vật
Độ phóng đại: $$k = -\frac{d’}{d} = -\frac{-6}{15} = \frac{6}{15} = 0.4$$
- $k > 0$: ảnh cùng chiều
- $|k| = 0.4 < 1$: ảnh nhỏ hơn vật
Chiều cao ảnh: $$h’ = k \times h = 0.4 \times 2 = 0.8 \text{ cm}$$
Kết luận: Ảnh ảo, cùng chiều, cao 0.8 cm (nhỏ hơn vật 2.5 lần), cách TK 6 cm về phía vật.
Bài 5: Tính độ tụ
Đề bài: Một thấu kính có tiêu cự f = 25 cm. Tính độ tụ của thấu kính?
Lời giải:
Bước 1: Đổi đơn vị $$f = 25 \text{ cm} = 0.25 \text{ m}$$
Bước 2: Tính độ tụ $$D = \frac{1}{f} = \frac{1}{0.25} = 4 \text{ điốp}$$
Kết luận: Độ tụ D = 4 dp (điốp)
Vì D > 0 → Đây là thấu kính hội tụ.
Bài 6: Ghép thấu kính
Đề bài: Ghép sát hai thấu kính: TKHT có $f_1 = 15$ cm và TKPK có $f_2 = -20$ cm. Tính tiêu cự và độ tụ của hệ thấu kính? Hệ là hội tụ hay phân kì?
Lời giải:
Tính tiêu cự hệ: $$\frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2} = \frac{1}{15} + \frac{1}{-20}$$
$$= \frac{1}{15} – \frac{1}{20} = \frac{4 – 3}{60} = \frac{1}{60}$$
$$f = 60 \text{ cm} = 0.6 \text{ m}$$
Tính độ tụ: $$D = \frac{1}{f} = \frac{1}{0.6} = \frac{10}{6} = \frac{5}{3} \approx 1.67 \text{ dp}$$
Kết luận:
- Tiêu cự: f = 60 cm = 0.6 m
- Độ tụ: D ≈ 1.67 dp
- Vì f > 0 và D > 0 → Hệ là thấu kính hội tụ
Bài 7: Kính lúp
Đề bài: Một kính lúp có tiêu cự f = 5 cm. Tính độ bội giác của kính lúp? Biết khoảng nhìn rõ ngắn nhất của mắt là 25 cm.
Lời giải:
Áp dụng công thức độ bội giác: $$G = \frac{D_{cc}}{f} = \frac{25}{5} = 5 \text{ lần}$$
Kết luận: Độ bội giác của kính lúp là 5 lần, nghĩa là khi nhìn qua kính lúp, ảnh lớn gấp 5 lần so với khi nhìn trực tiếp vật ở khoảng cách 25 cm.
IX. KẾT LUẬN
Bài viết đã trình bày hệ thống đầy đủ các công thức thấu kính và tiêu cự:
Công thức thấu kính cơ bản:
- Công thức chính: $\frac{1}{f} = \frac{1}{d} + \frac{1}{d’}$
- Độ phóng đại: $k = -\frac{d’}{d}$
- Độ tụ: $D = \frac{1}{f}$ (f tính bằng mét)
Quy ước dấu:
- TKHT: f > 0, có thể cho ảnh thật hoặc ảnh ảo
- TKPK: f < 0, luôn luôn cho ảnh ảo
- d’ > 0: ảnh thật, d’ < 0: ảnh ảo
- k > 0: ảnh cùng chiều, k < 0: ảnh ngược chiều
Tính chất ảnh:
- TKHT: Ảnh phụ thuộc vị trí vật (d < f: ảo, d > f: thật)
- TKPK: Luôn cho ảnh ảo, cùng chiều, nhỏ hơn vật
Công thức đặc biệt:
- Newton: $d_1 \cdot d_2 = f^2$
- Ghép TK: $\frac{1}{f} = \frac{1}{f_1} + \frac{1}{f_2}$
- Kính lúp: $G = \frac{25}{f(\text{cm})}$
7 bài tập mẫu có lời giải chi tiết từng bước
Công thức QUAN TRỌNG NHẤT
🔥 Công thức thấu kính:
$$\boxed{\frac{1}{f} = \frac{1}{d} + \frac{1}{d’}}$$
Quy ước dấu then chốt:
- TKHT: f > 0 (dương)
- TKPK: f < 0 (âm)
- Ảnh thật: d’ > 0
- Ảnh ảo: d’ < 0
Từ công thức này, suy ra:
- Vị trí ảnh: $d’ = \frac{fd}{d – f}$
- Độ phóng đại: $k = -\frac{d’}{d} = -\frac{f}{d – f}$
- Điều kiện tạo ảnh thật (TKHT): d > f

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
