Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ TAM GIÁC VUÔNG
- 1. Tam giác vuông là gì?
- 2. Quy ước ký hiệu
- II. TỈ SỐ LƯỢNG GIÁC TRONG TAM GIÁC VUÔNG
- 1. Định nghĩa các tỉ số lượng giác
- 2. Cách nhớ tỉ số lượng giác
- 3. Tính chất cơ bản
- 4. Bảng giá trị lượng giác đặc biệt
- III. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
- 1. Định lý Pythagore
- 2. Hệ thức về cạnh và góc
- 3. Hệ thức về đường cao
- 4. Hệ thức về cạnh và hình chiếu
- 5. Hệ thức liên hệ đường cao và cạnh
- 6. Bảng tổng hợp hệ thức
- IV. CÔNG THỨC TÍNH CẠNH VÀ GÓC
- 1. Tính cạnh khi biết cạnh và góc
- 2. Tính góc khi biết các cạnh
- 3. Các bài toán thực tế
- V. PHÂN BIỆT THEO LỚP
- A. Chương trình Lớp 8
- B. Chương trình Lớp 9
- C. Chương trình Lớp 10
- Bảng so sánh theo lớp
- VI. BÀI TẬP MẪU
- VII. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Lưu ý quan trọng
- VIII. KẾT LUẬN
- Lời khuyên học tập
I. GIỚI THIỆU VỀ TAM GIÁC VUÔNG
1. Tam giác vuông là gì?
Định nghĩa: Tam giác vuông là tam giác có một góc vuông, tức là có một góc bằng 90°.
Ký hiệu: Khi nói “tam giác ABC vuông tại A”, có nghĩa là góc ở đỉnh A bằng 90° (∠A = 90°).
Các thành phần của tam giác vuông:
Cạnh huyền: Là cạnh đối diện với góc vuông, đây là cạnh dài nhất trong tam giác vuông. Trong tam giác ABC vuông tại A, cạnh huyền là BC.
Hai cạnh góc vuông: Là hai cạnh tạo nên góc vuông. Trong tam giác ABC vuông tại A, hai cạnh góc vuông là AB và AC.
2. Quy ước ký hiệu
Sơ đồ tam giác vuông:
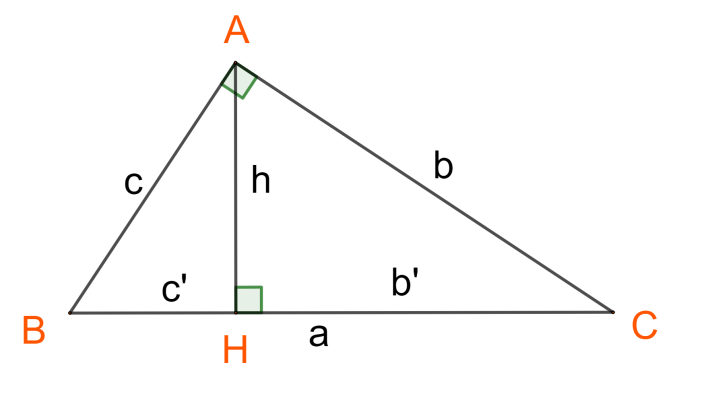
Quy ước chữ cái:
- Đỉnh A, B, C viết hoa
- Cạnh đối diện với đỉnh A là a (BC)
- Cạnh đối diện với đỉnh B là b (AC)
- Cạnh đối diện với đỉnh C là c (AB – cạnh huyền)
Trong tam giác ABC vuông tại A:
- Cạnh huyền: c = AB (cạnh đối diện góc vuông)
- Cạnh góc vuông thứ nhất: a = BC
- Cạnh góc vuông thứ hai: b = AC
- Các góc: ∠A = 90°, ∠B và ∠C là góc nhọn (< 90°)
II. TỈ SỐ LƯỢNG GIÁC TRONG TAM GIÁC VUÔNG
1. Định nghĩa các tỉ số lượng giác
Cho tam giác ABC vuông tại A, xét góc nhọn B:
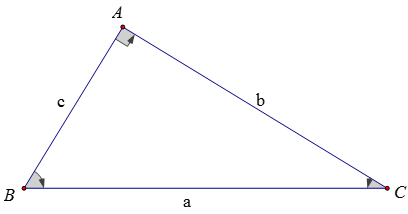
Xác định cạnh theo góc B:
- Cạnh đối: Là cạnh đối diện với góc B → cạnh AC (ký hiệu b)
- Cạnh kề: Là cạnh kề với góc B (không phải cạnh huyền) → cạnh BC (ký hiệu a)
- Cạnh huyền: Là cạnh đối diện góc vuông → cạnh AB (ký hiệu c)
📌 Bốn tỉ số lượng giác cơ bản của góc B:
$$\boxed{\sin B = \frac{\text{cạnh đối}}{\text{cạnh huyền}} = \frac{b}{c}}$$
$$\boxed{\cos B = \frac{\text{cạnh kề}}{\text{cạnh huyền}} = \frac{a}{c}}$$
$$\boxed{\tan B = \frac{\text{cạnh đối}}{\text{cạnh kề}} = \frac{b}{a}}$$
$$\boxed{\cot B = \frac{\text{cạnh kề}}{\text{cạnh đối}} = \frac{a}{b}}$$
Hai tỉ số lượng giác mở rộng (ít dùng trong chương trình phổ thông):
$$\sec B = \frac{\text{cạnh huyền}}{\text{cạnh kề}} = \frac{c}{a}$$
$$\csc B = \frac{\text{cạnh huyền}}{\text{cạnh đối}} = \frac{c}{b}$$
Lưu ý: Chương trình phổ thông (lớp 9, 10) tập trung vào 4 tỉ số: sin, cos, tan, cot.
2. Cách nhớ tỉ số lượng giác
Phương pháp 1: Khẩu quyết tiếng Việt
“Sin Đối Huyền, Cos Kề Huyền, Tan Đối Kề”
- Sin: Cạnh Đối chia Huyền
- Cos: Cạnh Kề chia Huyền
- Tan: Cạnh Đối chia Kề
- Cot: Cạnh Kề chia Đối (đảo ngược của Tan)
Phương pháp 2: Mẹo SOH-CAH-TOA (tiếng Anh)
Đây là mẹo nhớ nổi tiếng trong toán học quốc tế:
- SOH: Sin = Opposite/Hypotenuse (Đối/Huyền)
- CAH: Cos = Adjacent/Hypotenuse (Kề/Huyền)
- TOA: Tan = Opposite/Adjacent (Đối/Kề)
Phương pháp 3: Nhớ theo thứ tự
- Sin và Cos đều có Huyền ở mẫu
- Sin dùng Đối, Cos dùng Kề
- Tan không có Huyền, chỉ có Đối/Kề
- Cot là đảo ngược của Tan
3. Tính chất cơ bản
a) Tính chất hai góc phụ nhau
Định nghĩa: Trong tam giác vuông ABC vuông tại A, hai góc nhọn B và C là hai góc phụ nhau (tổng bằng 90°):
$$\angle B + \angle C = 90°$$
Hệ quả – Quan hệ tỉ số lượng giác:
$$\boxed{\sin B = \cos C}$$ $$\boxed{\cos B = \sin C}$$ $$\boxed{\tan B = \cot C}$$ $$\boxed{\cot B = \tan C}$$
Giải thích: Cạnh đối với góc B chính là cạnh kề với góc C, và ngược lại.
Ví dụ:
- $\sin 30° = \cos 60° = \frac{1}{2}$
- $\tan 30° = \cot 60° = \frac{1}{\sqrt{3}}$
b) Quan hệ giữa các tỉ số lượng giác
Công thức 1: Liên hệ giữa tan và sin, cos
$$\boxed{\tan B = \frac{\sin B}{\cos B}}$$
Chứng minh: $$\tan B = \frac{b/c}{a/c} = \frac{b}{a} = \frac{\sin B}{\cos B}$$
Công thức 2: Liên hệ giữa cot và sin, cos
$$\boxed{\cot B = \frac{\cos B}{\sin B} = \frac{1}{\tan B}}$$
Công thức 3: Hệ thức cơ bản (Pythagore lượng giác)
$$\boxed{\sin^2 B + \cos^2 B = 1}$$
Chứng minh: Từ định lý Pythagore $a^2 + b^2 = c^2$ $$\left(\frac{b}{c}\right)^2 + \left(\frac{a}{c}\right)^2 = \frac{a^2 + b^2}{c^2} = \frac{c^2}{c^2} = 1$$
Hệ quả:
- $\sin^2 B = 1 – \cos^2 B$
- $\cos^2 B = 1 – \sin^2 B$
Công thức 4: Hệ thức với tan và cot
$$1 + \tan^2 B = \frac{1}{\cos^2 B}$$
$$1 + \cot^2 B = \frac{1}{\sin^2 B}$$
4. Bảng giá trị lượng giác đặc biệt
Bảng giá trị của các góc đặc biệt:
| Góc | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin | $0$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1$ |
| cos | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ |
| tan | $0$ | $\frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$ | $1$ | $\sqrt{3}$ | không xđ |
| cot | không xđ | $\sqrt{3}$ | $1$ | $\frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$ | $0$ |
Mẹo nhớ giá trị sin: Dùng quy tắc “0, 1, 2, 3, 4 chia 4 rồi lấy căn”
- $\sin 0° = \sqrt{\frac{0}{4}} = 0$
- $\sin 30° = \sqrt{\frac{1}{4}} = \frac{1}{2}$
- $\sin 45° = \sqrt{\frac{2}{4}} = \frac{\sqrt{2}}{2}$
- $\sin 60° = \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2}$
- $\sin 90° = \sqrt{\frac{4}{4}} = 1$
Mẹo nhớ cos: Cos ngược lại với sin
- $\cos 0° = \sin 90° = 1$
- $\cos 30° = \sin 60° = \frac{\sqrt{3}}{2}$
- $\cos 45° = \sin 45° = \frac{\sqrt{2}}{2}$
- $\cos 60° = \sin 30° = \frac{1}{2}$
- $\cos 90° = \sin 0° = 0$
Mẹo nhớ tan: $\tan = \frac{\sin}{\cos}$
- $\tan 30° = \frac{1/2}{\sqrt{3}/2} = \frac{1}{\sqrt{3}}$
- $\tan 45° = \frac{\sqrt{2}/2}{\sqrt{2}/2} = 1$
- $\tan 60° = \frac{\sqrt{3}/2}{1/2} = \sqrt{3}$
III. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
1. Định lý Pythagore
Định lý: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
$$\boxed{c^2 = a^2 + b^2}$$
Hoặc viết đầy đủ: $$\text{(cạnh huyền)}^2 = \text{(cạnh góc vuông 1)}^2 + \text{(cạnh góc vuông 2)}^2$$
Các dạng biến đổi:
- $c = \sqrt{a^2 + b^2}$ (tính cạnh huyền)
- $a = \sqrt{c^2 – b^2}$ (tính cạnh góc vuông)
- $b = \sqrt{c^2 – a^2}$ (tính cạnh góc vuông)
Ví dụ 1: Tam giác vuông có hai cạnh góc vuông là 3cm và 4cm. Tính cạnh huyền.
Lời giải: $$c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \text{ cm}$$
Ví dụ 2: Tam giác vuông có cạnh huyền 13cm, một cạnh góc vuông 5cm. Tính cạnh còn lại.
Lời giải: $$b = \sqrt{13^2 – 5^2} = \sqrt{169 – 25} = \sqrt{144} = 12 \text{ cm}$$
2. Hệ thức về cạnh và góc
Cho tam giác ABC vuông tại A, với các cạnh a, b, c như đã quy ước:
📌 Công thức tính cạnh từ góc:
$$\boxed{a = c \sin B = c \cos C}$$ $$\boxed{b = c \sin C = c \cos B}$$ $$\boxed{a = b \tan B = b \cot C}$$ $$\boxed{b = a \tan C = a \cot B}$$
Ví dụ 3: Tam giác vuông có cạnh huyền c = 10cm, góc B = 30°. Tính cạnh b.
Lời giải: $$b = c \sin B = 10 \times \sin 30° = 10 \times \frac{1}{2} = 5 \text{ cm}$$
Ví dụ 4: Tam giác vuông có cạnh huyền c = 20cm, góc C = 60°. Tính cạnh a và b.
Lời giải:
- $a = c \cos C = 20 \times \cos 60° = 20 \times \frac{1}{2} = 10$ cm
- $b = c \sin C = 20 \times \sin 60° = 20 \times \frac{\sqrt{3}}{2} = 10\sqrt{3}$ cm
3. Hệ thức về đường cao
Cho tam giác ABC vuông tại A, kẻ đường cao AH từ đỉnh góc vuông xuống cạnh huyền BC:

Ký hiệu:
- $h = AH$ (đường cao)
- $b’ = HC$ (hình chiếu của AC lên BC)
- $c’ = HB$ (hình chiếu của AB lên BC)
- $a = BC = b’ + c’$ (cạnh huyền)
📌 Công thức về đường cao:
$$\boxed{h^2 = b’ \cdot c’}$$
Ý nghĩa: Bình phương đường cao bằng tích hai hình chiếu trên cạnh huyền.
Ví dụ 5: Trong tam giác vuông, hai hình chiếu lên cạnh huyền là 4cm và 9cm. Tính đường cao.
Lời giải: $$h = \sqrt{4 \times 9} = \sqrt{36} = 6 \text{ cm}$$
4. Hệ thức về cạnh và hình chiếu
📌 Công thức về cạnh góc vuông:
$$\boxed{b^2 = a \cdot b’}$$ $$\boxed{c^2 = a \cdot c’}$$
Ý nghĩa: Bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền với hình chiếu của cạnh đó lên cạnh huyền.
Ví dụ 6: Tam giác vuông có cạnh huyền 25cm, hình chiếu của một cạnh góc vuông lên cạnh huyền là 9cm. Tính cạnh góc vuông đó.
Lời giải: $$b = \sqrt{25 \times 9} = \sqrt{225} = 15 \text{ cm}$$
5. Hệ thức liên hệ đường cao và cạnh
📌 Công thức tính đường cao:
$$\boxed{h = \frac{b \cdot c}{a}}$$
Chứng minh: Dùng diện tích tam giác
- Cách 1: $S = \frac{1}{2}bc$ (hai cạnh góc vuông)
- Cách 2: $S = \frac{1}{2}ah$ (cạnh huyền và đường cao)
- Suy ra: $\frac{1}{2}bc = \frac{1}{2}ah$ → $h = \frac{bc}{a}$
📌 Công thức nghịch đảo:
$$\boxed{\frac{1}{h^2} = \frac{1}{b^2} + \frac{1}{c^2}}$$
Chứng minh: Từ $h = \frac{bc}{a}$ và $a^2 = b^2 + c^2$ (Pythagore)
$$h^2 = \frac{b^2c^2}{a^2} = \frac{b^2c^2}{b^2 + c^2}$$
Đảo ngược: $$\frac{1}{h^2} = \frac{b^2 + c^2}{b^2c^2} = \frac{1}{c^2} + \frac{1}{b^2}$$
Ví dụ 7: Tam giác vuông có hai cạnh góc vuông 6cm và 8cm. Tính đường cao ứng với cạnh huyền.
Lời giải:
Cách 1: Dùng công thức trực tiếp
- Cạnh huyền: $a = \sqrt{6^2 + 8^2} = 10$ cm
- Đường cao: $h = \frac{6 \times 8}{10} = \frac{48}{10} = 4.8$ cm
Cách 2: Dùng công thức nghịch đảo $$\frac{1}{h^2} = \frac{1}{6^2} + \frac{1}{8^2} = \frac{1}{36} + \frac{1}{64} = \frac{64 + 36}{2304} = \frac{100}{2304}$$ $$h^2 = \frac{2304}{100} = 23.04$$ $$h = 4.8 \text{ cm}$$
6. Bảng tổng hợp hệ thức
| Loại hệ thức | Công thức | Ý nghĩa |
|---|---|---|
| Pythagore | $a^2 = b^2 + c^2$ | Bình phương cạnh huyền |
| Đường cao | $h^2 = b’ \cdot c’$ | Bình phương đường cao |
| Cạnh – hình chiếu | $b^2 = a \cdot b’$, $c^2 = a \cdot c’$ | Bình phương cạnh góc vuông |
| Đường cao – cạnh | $h = \frac{bc}{a}$ | Đường cao từ tích hai cạnh |
| Nghịch đảo | $\frac{1}{h^2} = \frac{1}{b^2} + \frac{1}{c^2}$ | Tổng nghịch đảo bình phương |
IV. CÔNG THỨC TÍNH CẠNH VÀ GÓC
1. Tính cạnh khi biết cạnh và góc
Trường hợp 1: Biết cạnh huyền c và góc B
$$a = c \sin B$$ $$b = c \cos B$$
Ví dụ 8: Tam giác vuông có cạnh huyền 15cm, góc B = 40°. Tính các cạnh góc vuông.
Lời giải:
- $a = 15 \sin 40° \approx 15 \times 0.643 = 9.64$ cm
- $b = 15 \cos 40° \approx 15 \times 0.766 = 11.49$ cm
Trường hợp 2: Biết cạnh góc vuông a và góc B
$$c = \frac{a}{\sin B}$$ $$b = a \cot B = \frac{a}{\tan B}$$
Ví dụ 9: Tam giác vuông có cạnh góc vuông a = 8cm, góc B = 53°. Tính cạnh huyền và cạnh còn lại.
Lời giải:
- $c = \frac{8}{\sin 53°} \approx \frac{8}{0.8} = 10$ cm
- $b = \frac{8}{\tan 53°} \approx \frac{8}{1.327} = 6$ cm
Trường hợp 3: Biết cạnh góc vuông b và góc B
$$c = \frac{b}{\cos B}$$ $$a = b \tan B$$
2. Tính góc khi biết các cạnh
Cho tam giác ABC vuông tại A, biết các cạnh a, b, c:
$$\sin B = \frac{a}{c} \Rightarrow B = \arcsin\left(\frac{a}{c}\right)$$
$$\cos B = \frac{b}{c} \Rightarrow B = \arccos\left(\frac{b}{c}\right)$$
$$\tan B = \frac{a}{b} \Rightarrow B = \arctan\left(\frac{a}{b}\right)$$
Ví dụ 10: Tam giác vuông có cạnh đối diện góc B là 3cm, cạnh kề là 4cm. Tính góc B.
Lời giải: $$\tan B = \frac{3}{4} = 0.75$$ $$B = \arctan(0.75) \approx 36.87° \approx 36°52’$$
3. Các bài toán thực tế
Dạng 1: Đo chiều cao
Bài toán: Đứng cách chân tháp 50m, nhìn lên đỉnh tháp với góc nâng 30°. Tính chiều cao tháp (không kể chiều cao mắt người quan sát).
Lời giải: $$h = 50 \tan 30° = 50 \times \frac{1}{\sqrt{3}} = \frac{50\sqrt{3}}{3} \approx 28.87 \text{ m}$$
Dạng 2: Đo khoảng cách
Bài toán: Từ đỉnh tòa nhà cao 100m, nhìn xuống một điểm trên mặt đất với góc 45°. Tính khoảng cách từ chân tòa nhà đến điểm đó.
Lời giải: $$d = \frac{100}{\tan 45°} = \frac{100}{1} = 100 \text{ m}$$
Dạng 3: Độ dốc
Bài toán: Một con dốc dài 200m, cao 50m. Tính góc nghiêng của con dốc.
Lời giải: $$\sin \alpha = \frac{50}{200} = 0.25$$ $$\alpha = \arcsin(0.25) \approx 14.48° \approx 14°29’$$
V. PHÂN BIỆT THEO LỚP
A. Chương trình Lớp 8
Nội dung chính:
- Định lý Pythagore và ứng dụng
- Hệ thức về cạnh và đường cao (cơ bản)
- Các bài toán tính toán đơn giản
Công thức trọng tâm:
- Định lý Pythagore: $a^2 = b^2 + c^2$
- Hệ thức đường cao: $h^2 = b’ \cdot c’$
- Hệ thức cạnh: $b^2 = a \cdot b’$
Đặc điểm: Chưa học tỉ số lượng giác, chỉ tập trung vào quan hệ độ dài các cạnh.
B. Chương trình Lớp 9
Nội dung chính:
- Tỉ số lượng giác của góc nhọn: sin, cos, tan, cot
- Tính chất góc phụ nhau
- Giá trị lượng giác đặc biệt: 30°, 45°, 60°
- Hệ thức cơ bản: $\sin^2 + \cos^2 = 1$
Công thức trọng tâm:
$$\sin B = \frac{\text{đối}}{\text{huyền}}, \quad \cos B = \frac{\text{kề}}{\text{huyền}}, \quad \tan B = \frac{\text{đối}}{\text{kề}}$$
Ứng dụng:
- Giải tam giác vuông: Tính các cạnh và góc chưa biết
- Bài toán thực tế: Đo chiều cao, khoảng cách không thể tiếp cận trực tiếp
- Bài toán ứng dụng: Xây dựng, đo đạc, hàng hải
Đặc điểm: Đây là lần đầu học sinh được làm quen với khái niệm tỉ số lượng giác.
C. Chương trình Lớp 10
Nội dung chính:
- Mở rộng lượng giác lên đường tròn đơn vị
- Lượng giác của góc bất kỳ (0° đến 360°, hoặc số âm)
- Công thức lượng giác nâng cao
- Phương trình lượng giác
Công thức mới:
- Lượng giác các góc trong 4 góc phần tư
- Công thức cộng: $\sin(a \pm b)$, $\cos(a \pm b)$
- Công thức nhân đôi, nhân ba
- Công thức biến đổi tổng thành tích
- Phương trình lượng giác cơ bản
Đặc điểm: Lượng giác không còn giới hạn trong tam giác vuông, mở rộng thành lượng giác tổng quát.
Bảng so sánh theo lớp
| Lớp | Nội dung chính | Mức độ | Ứng dụng |
|---|---|---|---|
| Lớp 8 | Pythagore, hệ thức đường cao | Cơ bản | Tính độ dài cạnh |
| Lớp 9 | Tỉ số lượng giác (sin, cos, tan, cot) | Trung bình | Giải tam giác vuông, đo đạc |
| Lớp 10 | Lượng giác tổng quát, công thức nâng cao | Nâng cao | Phương trình, biến đổi |
VI. BÀI TẬP MẪU
Dạng 1: Tính cạnh bằng định lý Pythagore
Bài tập 1: Tam giác vuông có hai cạnh góc vuông là 5cm và 12cm. Tính cạnh huyền.
Lời giải:
Áp dụng định lý Pythagore: $$c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ cm}$$
Kết luận: Cạnh huyền dài 13 cm.
Dạng 2: Tính tỉ số lượng giác
Bài tập 2: Tam giác vuông có cạnh huyền 10cm, cạnh đối diện góc B là 6cm. Tính sin B, cos B, tan B, cot B.
Lời giải:
Bước 1: Tính cạnh kề (dùng Pythagore) $$a = \sqrt{10^2 – 6^2} = \sqrt{100 – 36} = \sqrt{64} = 8 \text{ cm}$$
Bước 2: Tính các tỉ số lượng giác
- $\sin B = \frac{6}{10} = \frac{3}{5} = 0.6$
- $\cos B = \frac{8}{10} = \frac{4}{5} = 0.8$
- $\tan B = \frac{6}{8} = \frac{3}{4} = 0.75$
- $\cot B = \frac{8}{6} = \frac{4}{3} \approx 1.333$
Kiểm tra: $\sin^2 B + \cos^2 B = 0.6^2 + 0.8^2 = 0.36 + 0.64 = 1$ ✓
Dạng 3: Tính cạnh từ tỉ số lượng giác
Bài tập 3: Tam giác vuông có cạnh huyền 20cm, góc B = 60°. Tính các cạnh góc vuông.
Lời giải:
Cạnh đối diện góc B: $$b = 20 \sin 60° = 20 \times \frac{\sqrt{3}}{2} = 10\sqrt{3} \approx 17.32 \text{ cm}$$
Cạnh kề góc B: $$a = 20 \cos 60° = 20 \times \frac{1}{2} = 10 \text{ cm}$$
Kết luận: Hai cạnh góc vuông là 10 cm và $10\sqrt{3}$ cm.
Dạng 4: Tính đường cao
Bài tập 4: Tam giác vuông có hai cạnh góc vuông 6cm và 8cm. Tính đường cao ứng với cạnh huyền.
Lời giải:
Bước 1: Tính cạnh huyền $$c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ cm}$$
Bước 2: Tính đường cao $$h = \frac{6 \times 8}{10} = \frac{48}{10} = 4.8 \text{ cm}$$
Kết luận: Đường cao ứng với cạnh huyền là 4.8 cm.
Dạng 5: Bài toán thực tế – Đo chiều cao
Bài tập 5: Từ điểm A cách chân tháp 30m, nhìn lên đỉnh tháp với góc nâng 45°. Tính chiều cao của tháp (giả sử mắt người quan sát ngang với chân tháp).
Lời giải:
Áp dụng công thức: $$h = 30 \tan 45° = 30 \times 1 = 30 \text{ m}$$
Kết luận: Chiều cao tháp là 30 mét.
Dạng 6: Tính góc từ cạnh
Bài tập 6: Tam giác vuông có cạnh đối 7cm, cạnh kề 24cm. Tính góc B (làm tròn đến phút).
Lời giải:
$$\tan B = \frac{7}{24} \approx 0.2917$$
$$B = \arctan(0.2917) \approx 16.26° \approx 16°16’$$
Kết luận: Góc B xấp xỉ 16°16′.
VII. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Tỉ số lượng giác – Khẩu quyết vàng
“Sin Đối Huyền, Cos Kề Huyền, Tan Đối Kề”
Đây là cách nhớ hiệu quả nhất, giúp bạn không bao giờ quên!
Góc phụ nhau
“Sin này bằng Cos kia”
Hai góc phụ nhau có:
- $\sin 30° = \cos 60°$
- $\sin 45° = \cos 45°$
- $\tan 30° = \cot 60°$
Định lý Pythagore
“Bình phương cạnh huyền = tổng bình phương hai cạnh góc vuông”
Luôn nhớ: $c^2 = a^2 + b^2$ (có lũy thừa 2!)
Đường cao
Công thức 1: $h^2 = b’ \cdot c’$ – “Bình phương đường cao = tích hai hình chiếu”
Công thức 2: $h = \frac{ab}{c}$ – “Tích hai cạnh góc vuông chia cho cạnh huyền”
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm cạnh đối và cạnh kề
Cách tránh: Luôn vẽ hình và xác định rõ góc đang xét, đánh dấu cạnh đối và cạnh kề.
❌ SAI LẦM 2: Quên căn khi dùng Pythagore
Sai: $c = a^2 + b^2$ ❌
Đúng: $c = \sqrt{a^2 + b^2}$ ✓
❌ SAI LẦM 3: Nhầm công thức đường cao
Sai: $h = b’ \cdot c’$ ❌ (thiếu bình phương)
Đúng: $h^2 = b’ \cdot c’$ hoặc $h = \sqrt{b’ \cdot c’}$ ✓
❌ SAI LẦM 4: Quên đổi đơn vị góc trong máy tính
Khi tính sin, cos, tan bằng máy tính, cần kiểm tra máy đang ở chế độ:
- DEG (độ – degree) → cho góc dạng 30°, 45°
- RAD (radian) → cho góc dạng π/6, π/4
Nếu nhầm chế độ, kết quả sẽ hoàn toàn sai!
3. Lưu ý quan trọng
Luôn vẽ hình và ghi rõ ký hiệu
Hình vẽ chuẩn giúp:
- Xác định đúng cạnh đối, kề, huyền
- Tránh nhầm lẫn công thức
- Dễ dàng kiểm tra kết quả
Kiểm tra kết quả bằng Pythagore
Sau khi tính được các cạnh, luôn kiểm tra: $$a^2 + b^2 = c^2$$
Nếu đúng → kết quả chính xác ✓
Giá trị sin và cos luôn ≤ 1
Trong tam giác vuông:
- $0 < \sin < 1$ (với góc nhọn)
- $0 < \cos < 1$ (với góc nhọn)
Nếu tính ra sin hoặc cos > 1 → Sai ngay!
Quan hệ giữa tan và cot
$$\tan B \times \cot B = 1$$
Nếu biết tan, tính ngay cot bằng cách lấy nghịch đảo.
VIII. KẾT LUẬN
Bài viết đã trình bày hệ thống đầy đủ công thức lượng giác trong tam giác vuông:
Tỉ số lượng giác cơ bản:
- Sin = Đối/Huyền
- Cos = Kề/Huyền
- Tan = Đối/Kề
- Cot = Kề/Đối
Định lý Pythagore: $c^2 = a^2 + b^2$
Hệ thức về đường cao:
- $h^2 = b’ \cdot c’$
- $h = \frac{ab}{c}$
Hệ thức về cạnh và hình chiếu: $b^2 = a \cdot b’$
Bảng giá trị đặc biệt: 30°, 45°, 60°
Phân biệt theo lớp: 8, 9, 10
6 dạng bài tập: Từ cơ bản đến thực tế
Lời khuyên học tập
📌 Học thuộc 4 tỉ số lượng giác cơ bản – Nền tảng của mọi bài toán
📌 Nhớ khẩu quyết “Sin Đối Huyền” – Mẹo đơn giản nhưng cực kỳ hiệu quả
📌 Vẽ hình chuẩn, ghi rõ ký hiệu – Tránh 90% sai lầm
📌 Luyện tập đa dạng các dạng bài – Từ lý thuyết đến thực tế
📌 Học thuộc bảng giá trị đặc biệt – 30°, 45°, 60° xuất hiện rất nhiều
📌 Kiểm tra kết quả bằng Pythagore – Phát hiện sai sót ngay lập tức

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
