Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ ĐA GIÁC
- 1. Đa giác là gì?
- 2. Phân loại đa giác
- II. CÔNG THỨC TỔNG QUÁT CHO ĐA GIÁC
- 1. Tổng các góc trong
- 2. Số đường chéo
- 3. Chu vi đa giác
- 4. Diện tích đa giác tổng quát
- III. CÔNG THỨC ĐA GIÁC ĐỀU
- 1. Góc trong đa giác đều
- 2. Góc ở tâm
- 3. Bán kính đường tròn ngoại tiếp
- 4. Bán kính đường tròn nội tiếp
- 5. Công thức diện tích đa giác đều
- Bảng công thức một số đa giác đều thường gặp
- IV. PHƯƠNG PHÁP TÍNH DIỆN TÍCH ĐA GIÁC
- Phương pháp 1: Chia tam giác
- Phương pháp 2: Công thức Shoelace (Tọa độ)
- Phương pháp 3: Công thức đa giác đều
- Phương pháp 4: Diện tích theo bán kính (Đa giác nội tiếp)
- V. BÀI TẬP THỰC TẾ
- VI. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Các lời khuyên hữu ích
- 4. Bảng tóm tắt công thức
- VII. KẾT LUẬN
- Tổng kết
- Tài liệu tham khảo và mở rộng
I. GIỚI THIỆU VỀ ĐA GIÁC
1. Đa giác là gì?
Định nghĩa: Đa giác là một hình phẳng khép kín được tạo thành bởi $n$ đoạn thẳng ($n \geq 3$), trong đó mỗi đoạn thẳng chỉ gặp hai đoạn thẳng khác tại các đầu mút.
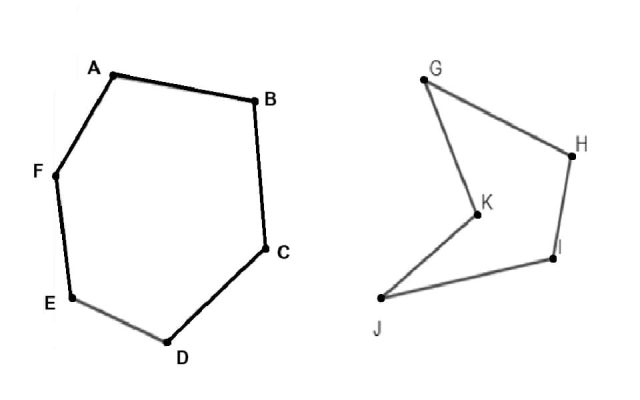
Các yếu tố cấu thành đa giác:
- Đỉnh: Là các điểm đầu mút của các đoạn thẳng. Đa giác $n$ cạnh có $n$ đỉnh.
- Cạnh: Là các đoạn thẳng nối các đỉnh liên tiếp nhau. Đa giác $n$ cạnh có $n$ cạnh.
- Góc trong: Là các góc tạo bởi hai cạnh liên tiếp tại mỗi đỉnh. Có $n$ góc trong.
- Đường chéo: Là đoạn thẳng nối hai đỉnh không kề nhau (không phải cạnh).
Ký hiệu: Đa giác thường được ký hiệu bằng các chữ cái đặt tại các đỉnh, theo thứ tự liên tiếp. Ví dụ: Ngũ giác ABCDE, Lục giác MNPQRS.
2. Phân loại đa giác
a) Theo độ lồi:
Đa giác lồi:
- Mọi góc trong đều nhỏ hơn 180°
- Không có phần lõm vào trong
- Bất kỳ đoạn thẳng nối hai điểm bất kỳ trong đa giác đều nằm hoàn toàn trong đa giác
- Ví dụ: Tam giác, hình vuông, ngũ giác đều, lục giác đều
Đa giác lõm:
- Có ít nhất một góc trong lớn hơn 180°
- Có phần lõm vào trong
- Tồn tại đoạn thẳng nối hai điểm trong đa giác nhưng nằm ngoài đa giác
- Ví dụ: Ngôi sao, hình mũi tên
b) Theo tính đều:
Đa giác đều (Regular Polygon):
- Tất cả các cạnh có độ dài bằng nhau
- Tất cả các góc trong có số đo bằng nhau
- Có tâm đối xứng và các trục đối xứng
- Ví dụ: Tam giác đều, hình vuông, ngũ giác đều, lục giác đều
Đa giác không đều:
- Các cạnh hoặc các góc không bằng nhau
- Không có tính đối xứng hoàn toàn
- Ví dụ: Hình chữ nhật (không phải hình vuông), hình thang, ngũ giác bất kỳ
c) Theo số cạnh:
- Tam giác ($n=3$): 3 cạnh, 3 góc
- Tứ giác ($n=4$): 4 cạnh, 4 góc (hình vuông, chữ nhật, thang, bình hành…)
- Ngũ giác ($n=5$): 5 cạnh, 5 góc
- Lục giác ($n=6$): 6 cạnh, 6 góc
- Thất giác ($n=7$): 7 cạnh, 7 góc
- Bát giác ($n=8$): 8 cạnh, 8 góc
- Cửu giác ($n=9$): 9 cạnh, 9 góc
- Thập giác ($n=10$): 10 cạnh, 10 góc
- Thập nhị giác ($n=12$): 12 cạnh, 12 góc
- …
II. CÔNG THỨC TỔNG QUÁT CHO ĐA GIÁC
1. Tổng các góc trong
Định lý: Đa giác lồi có $n$ cạnh có tổng các góc trong là:
$$\boxed{\sum \text{góc trong} = (n-2) \times 180°}$$
Chứng minh:
Phương pháp: Chia đa giác thành các tam giác từ một đỉnh.
Bước 1: Chọn một đỉnh bất kỳ của đa giác $n$ cạnh.
Bước 2: Từ đỉnh đó, kẻ các đường chéo đến tất cả các đỉnh không kề (có $n-3$ đỉnh như vậy).
Bước 3: Đa giác được chia thành $(n-2)$ tam giác.
Bước 4: Mỗi tam giác có tổng ba góc bằng 180°.
Bước 5: Tổng góc trong của đa giác = Tổng góc của $(n-2)$ tam giác = $(n-2) \times 180°$
Ví dụ 1: Tính tổng các góc trong của các đa giác sau:
a) Tứ giác ($n=4$): $$\sum = (4-2) \times 180° = 2 \times 180° = 360°$$
b) Ngũ giác ($n=5$): $$\sum = (5-2) \times 180° = 3 \times 180° = 540°$$
c) Lục giác ($n=6$): $$\sum = (6-2) \times 180° = 4 \times 180° = 720°$$
d) Bát giác ($n=8$): $$\sum = (8-2) \times 180° = 6 \times 180° = 1080°$$
Lưu ý: Công thức này áp dụng cho mọi đa giác lồi, không phân biệt đều hay không đều.
2. Số đường chéo
Định lý: Đa giác $n$ cạnh có số đường chéo là:
$$\boxed{d = \frac{n(n-3)}{2}}$$
Giải thích:
Bước 1: Từ mỗi đỉnh, ta có thể kẻ đường chéo đến $(n-3)$ đỉnh khác.
- Loại chính đỉnh đó: 1 đỉnh
- Loại 2 đỉnh kề: 2 đỉnh
- Còn lại: $n – 1 – 2 = n – 3$ đỉnh
Bước 2: Tổng số đường chéo từ tất cả các đỉnh: $n(n-3)$
Bước 3: Mỗi đường chéo được đếm 2 lần (từ hai đầu mút), nên số đường chéo thực tế: $$d = \frac{n(n-3)}{2}$$
Ví dụ 2: Tính số đường chéo của các đa giác:
a) Tam giác ($n=3$): $$d = \frac{3(3-3)}{2} = \frac{0}{2} = 0$$ (Tam giác không có đường chéo)
b) Tứ giác ($n=4$): $$d = \frac{4(4-3)}{2} = \frac{4 \times 1}{2} = 2$$
c) Ngũ giác ($n=5$): $$d = \frac{5(5-3)}{2} = \frac{5 \times 2}{2} = 5$$
d) Lục giác ($n=6$): $$d = \frac{6(6-3)}{2} = \frac{6 \times 3}{2} = 9$$
e) Bát giác ($n=8$): $$d = \frac{8(8-3)}{2} = \frac{8 \times 5}{2} = 20$$
f) Thập giác ($n=10$): $$d = \frac{10(10-3)}{2} = \frac{10 \times 7}{2} = 35$$
3. Chu vi đa giác
Định nghĩa: Chu vi đa giác là tổng độ dài tất cả các cạnh.
Công thức tổng quát:
$$\boxed{P = a_1 + a_2 + a_3 + … + a_n}$$
Trong đó: $a_1, a_2, …, a_n$ là độ dài các cạnh.
Với đa giác đều (tất cả các cạnh bằng nhau, độ dài cạnh là $a$):
$$\boxed{P = n \times a}$$
Ví dụ 3:
a) Tứ giác có các cạnh 3 cm, 5 cm, 4 cm, 6 cm: $$P = 3 + 5 + 4 + 6 = 18 \text{ cm}$$
b) Ngũ giác đều cạnh 7 cm: $$P = 5 \times 7 = 35 \text{ cm}$$
c) Lục giác đều cạnh 4.5 m: $$P = 6 \times 4.5 = 27 \text{ m}$$
4. Diện tích đa giác tổng quát
Có nhiều phương pháp tính diện tích đa giác tùy theo dữ liệu cho trước:
Phương pháp 1: Chia tam giác
Nguyên tắc: Chia đa giác thành các tam giác, tính diện tích từng tam giác rồi cộng lại.
Các bước:
- Chọn một đỉnh làm gốc
- Kẻ các đường chéo từ đỉnh đó đến các đỉnh khác
- Đa giác được chia thành $(n-2)$ tam giác
- Tính diện tích từng tam giác (dùng công thức Heron, hoặc công thức cơ bản)
- Cộng tổng diện tích
Ưu điểm: Trực quan, dễ hiểu
Nhược điểm: Tốn thời gian khi đa giác có nhiều cạnh
Phương pháp 2: Công thức Shoelace (Công thức dây giày)
Đây là công thức quan trọng nhất và được sử dụng rộng rãi trong thực tế.
Điều kiện: Biết tọa độ các đỉnh của đa giác.
Công thức:
Cho đa giác có các đỉnh $A_1(x_1, y_1), A_2(x_2, y_2), …, A_n(x_n, y_n)$ được sắp xếp theo thứ tự (thuận hoặc ngược chiều kim đồng hồ):
$$\boxed{S = \frac{1}{2}\left|\sum_{i=1}^{n} (x_i y_{i+1} – x_{i+1} y_i)\right|}$$
Với quy ước: $x_{n+1} = x_1$ và $y_{n+1} = y_1$
Hoặc viết dưới dạng khai triển:
$$S = \frac{1}{2}|x_1(y_2-y_n) + x_2(y_3-y_1) + x_3(y_4-y_2) + … + x_n(y_1-y_{n-1})|$$
Cách nhớ: Nhân chéo theo hình dây giày, lấy hiệu rồi chia 2, lấy trị tuyệt đối.
Ví dụ 4: Tính diện tích tứ giác ABCD có tọa độ:
- $A(0, 0)$
- $B(4, 0)$
- $C(4, 3)$
- $D(0, 3)$
Lời giải:
Áp dụng công thức Shoelace: $$S = \frac{1}{2}|x_1(y_2-y_4) + x_2(y_3-y_1) + x_3(y_4-y_2) + x_4(y_1-y_3)|$$
Thay số: $$S = \frac{1}{2}|0(0-3) + 4(3-0) + 4(3-0) + 0(0-3)|$$ $$= \frac{1}{2}|0 + 12 + 12 + 0|$$ $$= \frac{1}{2} \times 24 = 12 \text{ đvdt}$$
Kiểm tra: Đây là hình chữ nhật $4 \times 3 = 12$ ✓
Lưu ý quan trọng:
- Phải sắp xếp các đỉnh theo thứ tự (cùng chiều)
- Luôn lấy trị tuyệt đối của kết quả
- Công thức áp dụng cho mọi đa giác lồi và cả đa giác lõm
III. CÔNG THỨC ĐA GIÁC ĐỀU
1. Góc trong đa giác đều
Định lý: Đa giác đều $n$ cạnh có mỗi góc trong bằng:
$$\boxed{\alpha = \frac{(n-2) \times 180°}{n}}$$
Chứng minh:
- Tổng các góc trong = $(n-2) \times 180°$
- Đa giác đều có $n$ góc bằng nhau
- Mỗi góc = $\frac{\text{Tổng}}{n} = \frac{(n-2) \times 180°}{n}$
Ví dụ 5: Tính số đo mỗi góc trong của các đa giác đều:
a) Tam giác đều ($n=3$): $$\alpha = \frac{(3-2) \times 180°}{3} = \frac{180°}{3} = 60°$$
b) Tứ giác đều (Hình vuông) ($n=4$): $$\alpha = \frac{(4-2) \times 180°}{4} = \frac{360°}{4} = 90°$$
c) Ngũ giác đều ($n=5$): $$\alpha = \frac{(5-2) \times 180°}{5} = \frac{540°}{5} = 108°$$
d) Lục giác đều ($n=6$): $$\alpha = \frac{(6-2) \times 180°}{6} = \frac{720°}{6} = 120°$$
e) Bát giác đều ($n=8$): $$\alpha = \frac{(8-2) \times 180°}{8} = \frac{1080°}{8} = 135°$$
f) Thập giác đều ($n=10$): $$\alpha = \frac{(10-2) \times 180°}{10} = \frac{1440°}{10} = 144°$$
Nhận xét: Khi $n$ càng lớn, góc trong càng gần 180° (đa giác càng gần hình tròn).
2. Góc ở tâm
Định nghĩa: Góc ở tâm là góc tạo bởi hai bán kính nối tâm với hai đỉnh liên tiếp.
Công thức:
$$\boxed{\beta = \frac{360°}{n}}$$
Ví dụ 6:
a) Tam giác đều: $\beta = \frac{360°}{3} = 120°$
b) Tứ giác đều: $\beta = \frac{360°}{4} = 90°$
c) Ngũ giác đều: $\beta = \frac{360°}{5} = 72°$
d) Lục giác đều: $\beta = \frac{360°}{6} = 60°$
e) Bát giác đều: $\beta = \frac{360°}{8} = 45°$
Mối quan hệ: $\alpha + \beta = 180°$ (không phải luôn đúng, chỉ đúng với một số trường hợp đặc biệt)
3. Bán kính đường tròn ngoại tiếp
Định nghĩa: Đường tròn ngoại tiếp đa giác đều là đường tròn đi qua tất cả các đỉnh. Bán kính $R$ là khoảng cách từ tâm đến đỉnh.
Công thức:
Cho đa giác đều $n$ cạnh, cạnh có độ dài $a$:
$$\boxed{R = \frac{a}{2\sin\frac{180°}{n}}}$$
Hoặc ngược lại:
$$\boxed{a = 2R\sin\frac{180°}{n}}$$
Ví dụ 7:
a) Tam giác đều cạnh $a$: $$R = \frac{a}{2\sin 60°} = \frac{a}{2 \times \frac{\sqrt{3}}{2}} = \frac{a}{\sqrt{3}} = \frac{a\sqrt{3}}{3}$$
b) Hình vuông cạnh $a$: $$R = \frac{a}{2\sin 45°} = \frac{a}{2 \times \frac{\sqrt{2}}{2}} = \frac{a}{\sqrt{2}} = \frac{a\sqrt{2}}{2}$$
c) Lục giác đều cạnh $a$: $$R = \frac{a}{2\sin 30°} = \frac{a}{2 \times 0.5} = a$$
Tính chất đặc biệt: Chỉ có lục giác đều có $R = a$!
4. Bán kính đường tròn nội tiếp
Định nghĩa: Đường tròn nội tiếp đa giác đều là đường tròn tiếp xúc với tất cả các cạnh. Bán kính $r$ là khoảng cách từ tâm đến cạnh (vuông góc).
Công thức:
$$\boxed{r = \frac{a}{2\tan\frac{180°}{n}}}$$
Mối quan hệ với $R$:
$$\boxed{r = R\cos\frac{180°}{n}}$$
Ví dụ 8:
a) Tam giác đều cạnh $a$: $$r = \frac{a}{2\tan 60°} = \frac{a}{2\sqrt{3}} = \frac{a\sqrt{3}}{6}$$
b) Hình vuông cạnh $a$: $$r = \frac{a}{2\tan 45°} = \frac{a}{2 \times 1} = \frac{a}{2}$$
c) Lục giác đều cạnh $a$: $$r = \frac{a}{2\tan 30°} = \frac{a}{2 \times \frac{1}{\sqrt{3}}} = \frac{a\sqrt{3}}{2}$$
5. Công thức diện tích đa giác đều
Đây là công thức quan trọng nhất cho đa giác đều.
CÔNG THỨC CHÍNH (theo cạnh):
$$\boxed{S = \frac{na^2}{4\tan\frac{180°}{n}}}$$
Hoặc dạng khác:
$$\boxed{S = \frac{na^2}{4} \cot\frac{180°}{n}}$$
(Vì $\cot\theta = \frac{1}{\tan\theta}$)
Chứng minh:
Bước 1: Chia đa giác đều thành $n$ tam giác cân bằng nhau (từ tâm đến các đỉnh).
Bước 2: Mỗi tam giác có:
- Đáy = $a$ (cạnh đa giác)
- Chiều cao = $r$ (bán kính nội tiếp)
Bước 3: Diện tích mỗi tam giác: $$S_{\triangle} = \frac{a \cdot r}{2}$$
Bước 4: Tổng diện tích: $$S = n \times S_{\triangle} = n \times \frac{a \cdot r}{2} = \frac{nar}{2}$$
Bước 5: Thay $r = \frac{a}{2\tan\frac{180°}{n}}$: $$S = \frac{na}{2} \times \frac{a}{2\tan\frac{180°}{n}} = \frac{na^2}{4\tan\frac{180°}{n}}$$
Công thức khác:
Theo bán kính ngoại tiếp $R$:
$$\boxed{S = \frac{nR^2}{2}\sin\frac{360°}{n}}$$
Theo bán kính nội tiếp $r$ và cạnh $a$:
$$\boxed{S = \frac{nar}{2}}$$
Bảng công thức một số đa giác đều thường gặp
| Đa giác | n | Góc trong | Góc ở tâm | Diện tích (cạnh $a$) |
|---|---|---|---|---|
| Tam giác đều | 3 | 60° | 120° | $\frac{a^2\sqrt{3}}{4}$ |
| Tứ giác đều (Vuông) | 4 | 90° | 90° | $a^2$ |
| Ngũ giác đều | 5 | 108° | 72° | $\frac{a^2\sqrt{25+10\sqrt{5}}}{4} \approx 1.72a^2$ |
| Lục giác đều | 6 | 120° | 60° | $\frac{3a^2\sqrt{3}}{2} \approx 2.60a^2$ |
| Thất giác đều | 7 | ~128.57° | ~51.43° | $\frac{7a^2}{4}\cot 25.71° \approx 3.63a^2$ |
| Bát giác đều | 8 | 135° | 45° | $2a^2(1+\sqrt{2}) \approx 4.83a^2$ |
| Thập giác đều | 10 | 144° | 36° | $\frac{5a^2}{2}\cot 18° \approx 7.69a^2$ |
| Thập nhị giác đều | 12 | 150° | 30° | $3a^2(2+\sqrt{3}) \approx 11.20a^2$ |
Lưu ý: Công thức ngũ giác và các đa giác $n \geq 7$ (trừ lục giác) khá phức tạp, trong thực tế thường dùng công thức tổng quát hoặc máy tính.
IV. PHƯƠNG PHÁP TÍNH DIỆN TÍCH ĐA GIÁC
Phương pháp 1: Chia tam giác
Nguyên tắc: Chia đa giác thành các tam giác, tính diện tích từng tam giác rồi cộng lại.
Quy trình:
Bước 1: Chọn một đỉnh làm gốc (thường chọn đỉnh thuận tiện nhất).
Bước 2: Kẻ các đường chéo từ đỉnh đó đến tất cả các đỉnh không kề nhau.
Bước 3: Đa giác được chia thành $(n-2)$ tam giác.
Bước 4: Tính diện tích từng tam giác bằng:
- Công thức cơ bản: $S = \frac{1}{2} \times \text{đáy} \times \text{chiều cao}$
- Công thức Heron: $S = \sqrt{p(p-a)(p-b)(p-c)}$ với $p = \frac{a+b+c}{2}$
- Công thức tọa độ (nếu biết tọa độ)
Bước 5: Tổng diện tích = Tổng diện tích các tam giác.
Ví dụ 9: Tính diện tích ngũ giác ABCDE
Phương pháp:
- Từ đỉnh A, kẻ đường chéo đến C và D
- Ngũ giác được chia thành 3 tam giác: $\triangle ABC$, $\triangle ACD$, $\triangle ADE$
- Diện tích: $S = S_{\triangle ABC} + S_{\triangle ACD} + S_{\triangle ADE}$
Ưu điểm:
- Trực quan, dễ hình dung
- Áp dụng được khi biết độ dài cạnh và chiều cao
Nhược điểm:
- Tốn thời gian khi đa giác có nhiều cạnh
- Cần tính nhiều tam giác riêng lẻ
Phương pháp 2: Công thức Shoelace (Tọa độ)
Điều kiện: Biết tọa độ tất cả các đỉnh của đa giác.
Ưu điểm:
- Nhanh chóng, chính xác
- Chỉ cần một công thức duy nhất
- Áp dụng được cho mọi loại đa giác (đều, không đều, lồi, lõm)
Công thức:
Cho đa giác có đỉnh $A_1(x_1, y_1), A_2(x_2, y_2), …, A_n(x_n, y_n)$:
$$S = \frac{1}{2}\left|\sum_{i=1}^{n} (x_i y_{i+1} – x_{i+1} y_i)\right|$$
Quy trình tính:
Bước 1: Sắp xếp các đỉnh theo thứ tự (thuận hoặc ngược chiều kim đồng hồ).
Bước 2: Viết bảng tọa độ:
x₁ y₁
x₂ y₂
x₃ y₃
...
xₙ yₙ
x₁ y₁ (lặp lại điểm đầu)
Bước 3: Tính tích chéo:
- Nhân chéo xuống: $x_1y_2 + x_2y_3 + … + x_ny_1$
- Nhân chéo lên: $x_2y_1 + x_3y_2 + … + x_1y_n$
Bước 4: Lấy hiệu, chia 2, lấy trị tuyệt đối: $$S = \frac{1}{2}|(\text{tổng xuống}) – (\text{tổng lên})|$$
Ví dụ 10: Tính diện tích ngũ giác có tọa độ các đỉnh:
- $A(0, 0)$
- $B(2, 0)$
- $C(3, 2)$
- $D(1, 3)$
- $E(-1, 2)$
Lời giải:
Bước 1: Lập bảng:
x y
0 0
2 0
3 2
1 3
-1 2
0 0 (lặp lại)
Bước 2: Tính tích chéo xuống: $$0 \times 0 + 2 \times 2 + 3 \times 3 + 1 \times 2 + (-1) \times 0$$ $$= 0 + 4 + 9 + 2 + 0 = 15$$
Bước 3: Tính tích chéo lên: $$2 \times 0 + 3 \times 0 + 1 \times 2 + (-1) \times 3 + 0 \times 2$$ $$= 0 + 0 + 2 – 3 + 0 = -1$$
Bước 4: Tính diện tích: $$S = \frac{1}{2}|15 – (-1)| = \frac{1}{2} \times 16 = 8 \text{ đvdt}$$
Kết luận: Diện tích ngũ giác là 8 đơn vị diện tích.
Phương pháp 3: Công thức đa giác đều
Điều kiện: Đa giác là đa giác đều (tất cả cạnh và góc bằng nhau).
Công thức:
$$S = \frac{na^2}{4\tan\frac{180°}{n}}$$
Quy trình:
- Xác định số cạnh $n$
- Xác định độ dài cạnh $a$
- Thay vào công thức
Ví dụ 11: Bát giác đều có cạnh 5 cm. Tính diện tích.
Lời giải:
- $n = 8$, $a = 5$ cm
- $\frac{180°}{8} = 22.5°$
- $\tan 22.5° \approx 0.414$
$$S = \frac{8 \times 25}{4 \times 0.414} = \frac{200}{1.656} \approx 120.8 \text{ cm}^2$$
Hoặc dùng công thức chính xác cho bát giác: $$S = 2a^2(1+\sqrt{2}) = 2 \times 25 \times (1 + 1.414) = 50 \times 2.414 = 120.7 \text{ cm}^2$$
Phương pháp 4: Diện tích theo bán kính (Đa giác nội tiếp)
Điều kiện: Đa giác đều nội tiếp trong đường tròn bán kính $R$.
Công thức:
$$S = \frac{nR^2}{2}\sin\frac{360°}{n}$$
Ví dụ 12: Ngũ giác đều nội tiếp đường tròn bán kính 10 cm.
Lời giải:
- $n = 5$, $R = 10$ cm
- $\frac{360°}{5} = 72°$
- $\sin 72° \approx 0.951$
$$S = \frac{5 \times 100}{2} \times 0.951 = 250 \times 0.951 = 237.8 \text{ cm}^2$$
V. BÀI TẬP THỰC TẾ
Bài tập 1: Tính diện tích mảnh đất
Đề bài: Một mảnh đất có dạng ngũ giác với tọa độ các đỉnh (đơn vị: mét):
- $A(0, 0)$
- $B(20, 5)$
- $C(25, 20)$
- $D(10, 30)$
- $E(-5, 15)$
Tính diện tích mảnh đất để làm thủ tục cấp sổ đỏ.
Lời giải:
Áp dụng công thức Shoelace:
Bước 1: Lập bảng tọa độ:
x y
0 0
20 5
25 20
10 30
-5 15
0 0
Bước 2: Tính tích chéo xuống: $$0 \times 5 + 20 \times 20 + 25 \times 30 + 10 \times 15 + (-5) \times 0$$ $$= 0 + 400 + 750 + 150 + 0 = 1300$$
Bước 3: Tính tích chéo lên: $$20 \times 0 + 25 \times 5 + 10 \times 20 + (-5) \times 30 + 0 \times 15$$ $$= 0 + 125 + 200 – 150 + 0 = 175$$
Bước 4: Tính diện tích: $$S = \frac{1}{2}|1300 – 175| = \frac{1}{2} \times 1125 = 562.5 \text{ m}^2$$
Kết luận: Diện tích mảnh đất là 562.5 m².
Ứng dụng: Đo đạc địa chính, thẩm định giá đất, làm sổ đỏ, quy hoạch sử dụng đất.
Bài tập 2: Thiết kế biển báo giao thông
Đề bài: Biển báo “STOP” (Dừng lại) có dạng bát giác đều. Khoảng cách giữa hai cạnh đối diện (đường kính đường tròn nội tiếp) là 60 cm. Tính diện tích cần sơn màu đỏ cho biển báo.
Lời giải:
Bước 1: Tìm bán kính nội tiếp
- Đường kính nội tiếp = $2r = 60$ cm
- Bán kính nội tiếp: $r = 30$ cm
Bước 2: Tìm cạnh bát giác Từ công thức: $r = \frac{a}{2\tan\frac{180°}{8}}$
$$30 = \frac{a}{2\tan 22.5°}$$ $$a = 60 \times \tan 22.5° = 60 \times 0.414 \approx 24.84 \text{ cm}$$
Bước 3: Tính diện tích $$S = 2a^2(1+\sqrt{2}) = 2 \times (24.84)^2 \times (1 + 1.414)$$ $$= 2 \times 617 \times 2.414 \approx 2979 \text{ cm}^2 \approx 0.30 \text{ m}^2$$
Kết luận: Diện tích cần sơn là khoảng 0.30 m² (2979 cm²).
Ứng dụng: Thiết kế biển báo giao thông, tính toán vật liệu sơn, chi phí sản xuất.
Bài tập 3: Sân chơi hình ngũ giác
Đề bài: Một sân chơi trẻ em có dạng ngũ giác đều với chu vi 50 mét.
a) Tính độ dài mỗi cạnh b) Tính diện tích sân chơi c) Chi phí làm cỏ nhân tạo là 60,000 đồng/m². Tính tổng chi phí.
Lời giải:
Câu a) Tính cạnh: $$a = \frac{P}{n} = \frac{50}{5} = 10 \text{ m}$$
Câu b) Tính diện tích: $$S = \frac{na^2}{4\tan\frac{180°}{n}} = \frac{5 \times 100}{4\tan 36°}$$
Với $\tan 36° \approx 0.727$: $$S = \frac{500}{4 \times 0.727} = \frac{500}{2.908} \approx 172 \text{ m}^2$$
Câu c) Tính chi phí: $$\text{Chi phí} = 172 \times 60,000 = 10,320,000 \text{ đồng}$$
Kết luận:
- Mỗi cạnh: 10 m
- Diện tích: 172 m²
- Tổng chi phí làm cỏ: 10,320,000 đồng
Ứng dụng: Quy hoạch khu vui chơi, công viên, dự toán chi phí thi công.
Bài tập 4: Logo ngôi sao năm cánh
Đề bài: Logo công ty có hình ngôi sao 5 cánh. Phần bên trong là ngũ giác đều có cạnh 4 cm. Tính diện tích phần ngũ giác để in màu vàng.
Lời giải:
Áp dụng công thức ngũ giác đều: $$S = \frac{5 \times 16}{4\tan 36°} = \frac{80}{4 \times 0.727} = \frac{80}{2.908} \approx 27.5 \text{ cm}^2$$
Hoặc dùng công thức chính xác: $$S = \frac{a^2\sqrt{25+10\sqrt{5}}}{4} = \frac{16 \times \sqrt{25 + 22.36}}{4} = \frac{16 \times 6.88}{4} \approx 27.5 \text{ cm}^2$$
Kết luận: Diện tích phần ngũ giác cần in là khoảng 27.5 cm².
Ứng dụng: Thiết kế logo, biểu tượng thương hiệu, tính chi phí in ấn.
Bài tập 5: Gạch bát giác lát sàn
Đề bài: Gạch lát sàn có dạng bát giác đều với cạnh 15 cm, kết hợp với gạch vuông nhỏ ở khoảng trống. Tính diện tích một viên gạch bát giác.
Lời giải:
Áp dụng công thức bát giác đều: $$S = 2a^2(1+\sqrt{2}) = 2 \times 225 \times (1 + 1.414)$$ $$= 450 \times 2.414 = 1086.3 \text{ cm}^2$$
Kết luận: Diện tích một viên gạch bát giác là khoảng 1086 cm² ≈ 0.11 m².
Ứng dụng: Tính toán vật liệu xây dựng, thiết kế nội thất, ước lượng số viên gạch cần dùng.
Bài tập 6: Phân tích ranh giới hành chính
Đề bài: Một xã có ranh giới dạng lục giác (không đều) với tọa độ GPS của 6 đỉnh (đơn vị: km):
- $A(0, 0)$
- $B(5, 2)$
- $C(8, 7)$
- $D(6, 12)$
- $E(2, 10)$
- $F(-2, 5)$
Tính diện tích xã để báo cáo lên cấp trên.
Lời giải:
Áp dụng công thức Shoelace cho 6 điểm:
Tích chéo xuống: $$0 \times 2 + 5 \times 7 + 8 \times 12 + 6 \times 10 + 2 \times 5 + (-2) \times 0$$ $$= 0 + 35 + 96 + 60 + 10 + 0 = 201$$
Tích chéo lên: $$5 \times 0 + 8 \times 2 + 6 \times 7 + 2 \times 12 + (-2) \times 10 + 0 \times 5$$ $$= 0 + 16 + 42 + 24 – 20 + 0 = 62$$
Diện tích: $$S = \frac{1}{2}|201 – 62| = \frac{139}{2} = 69.5 \text{ km}^2$$
Kết luận: Diện tích xã là 69.5 km² = 6,950 ha.
Ứng dụng: Quản lý hành chính, quy hoạch vùng, GIS, bản đồ số, thống kê dân số và diện tích.
VI. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Tổng góc trong:
“Trừ hai rồi nhân 180”
$$\sum \text{góc trong} = (n-2) \times 180°$$
Cách nhớ: Số tam giác = $n – 2$, mỗi tam giác có 180°
Số đường chéo:
“n nhân n trừ ba, chia đôi”
$$d = \frac{n(n-3)}{2}$$
Cách nhớ: Từ mỗi đỉnh kẻ $(n-3)$ đường chéo, có $n$ đỉnh nhưng đếm 2 lần.
Diện tích đa giác đều:
“n lần a bình, chia 4, nhân cot góc tâm trên 2”
$$S = \frac{na^2}{4}\cot\frac{180°}{n}$$
Hoặc nhớ: $$S = \frac{na^2}{4\tan\frac{180°}{n}}$$
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Quên chia 2 khi tính số đường chéo
Sai:
- Số đường chéo = $n(n-3)$ ❌
Đúng:
- Số đường chéo = $\frac{n(n-3)}{2}$ ✓
Lý do: Mỗi đường chéo được đếm 2 lần.
❌ SAI LẦM 2: Sai thứ tự điểm trong công thức Shoelace
Sai:
- Sắp xếp điểm ngẫu nhiên ❌
Đúng:
- Sắp xếp điểm theo thứ tự (cùng chiều kim đồng hồ hoặc ngược chiều) ✓
❌ SAI LẦM 3: Quên trị tuyệt đối trong Shoelace
Sai:
- $S = \frac{1}{2}(…)$ (có thể âm) ❌
Đúng:
- $S = \frac{1}{2}|…|$ (luôn dương) ✓
❌ SAI LẦM 4: Nhầm độ và radian khi tính lượng giác
Cần nhớ:
- Công thức dùng độ ($°$)
- Máy tính phải để chế độ DEG (degree)
- Không dùng radian trừ khi đề yêu cầu
3. Các lời khuyên hữu ích
Luôn sắp xếp điểm theo thứ tự (thuận hoặc ngược chiều kim đồng hồ) khi dùng Shoelace
Luôn lấy trị tuyệt đối kết quả cuối cùng trong công thức Shoelace
Vẽ hình để kiểm tra – Hình vẽ giúp phát hiện lỗi sắp xếp điểm
Kiểm tra đơn vị – Diện tích phải có đơn vị bình phương (m², cm², km²,…)
Dùng công thức phù hợp:
- Biết tọa độ → Dùng Shoelace
- Đa giác đều → Dùng công thức đa giác đều
- Không biết tọa độ → Chia tam giác
4. Bảng tóm tắt công thức
| Công thức | Biểu thức | Áp dụng |
|---|---|---|
| Tổng góc trong | $(n-2) \times 180°$ | Mọi đa giác lồi |
| Góc trong (đều) | $\frac{(n-2) \times 180°}{n}$ | Đa giác đều |
| Góc ở tâm (đều) | $\frac{360°}{n}$ | Đa giác đều |
| Số đường chéo | $\frac{n(n-3)}{2}$ | Mọi đa giác |
| Chu vi (đều) | $P = na$ | Đa giác đều |
| Diện tích (Shoelace) | $S = \frac{1}{2}|\sum(x_iy_{i+1} – x_{i+1}y_i)|$ | Biết tọa độ |
| Diện tích (đều, cạnh) | $S = \frac{na^2}{4\tan\frac{180°}{n}}$ | Đa giác đều |
| Diện tích (đều, R) | $S = \frac{nR^2}{2}\sin\frac{360°}{n}$ | Đa giác nội tiếp |
| Bán kính ngoại | $R = \frac{a}{2\sin\frac{180°}{n}}$ | Đa giác đều |
| Bán kính nội | $r = \frac{a}{2\tan\frac{180°}{n}}$ | Đa giác đều |
VII. KẾT LUẬN
Tổng kết
Bài viết đã trình bày hệ thống công thức đa giác đầy đủ và toàn diện:
Công thức tổng quát cho mọi đa giác:
- Tổng góc trong: $(n-2) \times 180°$
- Số đường chéo: $\frac{n(n-3)}{2}$
- Chu vi: $P = a_1 + a_2 + … + a_n$
- Diện tích (Shoelace): $S = \frac{1}{2}|\sum(x_iy_{i+1} – x_{i+1}y_i)|$
Công thức đa giác đều:
- Góc trong: $\frac{(n-2) \times 180°}{n}$
- Góc ở tâm: $\frac{360°}{n}$
- Bán kính ngoại tiếp: $R = \frac{a}{2\sin\frac{180°}{n}}$
- Bán kính nội tiếp: $r = \frac{a}{2\tan\frac{180°}{n}}$
- Diện tích: $S = \frac{na^2}{4\tan\frac{180°}{n}}$
4 phương pháp tính diện tích:
- Chia tam giác
- Công thức Shoelace (tọa độ) ⭐
- Công thức đa giác đều
- Theo bán kính ngoại tiếp
6 bài tập thực tế ứng dụng:
- Đo đạc đất đai, thiết kế biển báo
- Quy hoạch sân chơi, thiết kế logo
- Tính vật liệu xây dựng, GIS
Tài liệu tham khảo và mở rộng
Các chủ đề liên quan:
Cơ bản:
- [Công Thức Tam Giác – Tổng Hợp Đầy Đủ]
- [Công Thức Tứ Giác – Chu Vi và Diện Tích]
- [Công Thức Lục Giác Đều – Chi Tiết]

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
