Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ HÌNH CHÓP
- 1. Định nghĩa hình chóp
- 2. Các yếu tố của hình chóp
- 3. Phân loại hình chóp
- II. CÔNG THỨC TỔNG QUÁT CỦA HÌNH CHÓP
- 1. Công thức thể tích khối chóp (QUAN TRỌNG NHẤT)
- 2. Công thức diện tích toàn phần
- 3. Các công thức liên quan
- III. CÔNG THỨC HÌNH CHÓP TAM GIÁC ĐỀU
- 1. Định nghĩa
- 2. Các công thức cơ bản
- 3. Công thức thể tích
- 4. Diện tích xung quanh
- IV. CÔNG THỨC HÌNH CHÓP TỨ GIÁC ĐỀU
- 1. Định nghĩa
- 2. Các công thức cơ bản
- 3. Công thức thể tích
- 4. Diện tích xung quanh
- V. CÔNG THỨC HÌNH CHÓP ĐỀU TỔNG QUÁT
- 1. Hình chóp đều n-giác
- 2. Bảng công thức nhanh cho các chóp đều
- VI. CÔNG THỨC HÌNH CHÓP CỤT
- 1. Định nghĩa hình chóp cụt
- 2. Công thức thể tích hình chóp cụt
- 3. Công thức chóp cụt tứ giác đều
- 4. Diện tích xung quanh chóp cụt đều
- 5. Mối liên hệ với hình chóp ban đầu
- VII. CÁC DẠNG BÀI TẬP TRỌNG TÂM
- Dạng 1: Tính thể tích khi biết diện tích đáy và chiều cao
- Dạng 2: Tính chiều cao khi biết thể tích và đáy
- Dạng 3: Hình chóp có các mặt bên vuông góc với đáy
- Dạng 4: Tính tỷ số thể tích
- Dạng 5: Hình chóp đều – Tính các yếu tố khi biết góc
- Dạng 6: Khoảng cách và góc trong hình chóp
- VIII. BẢNG CÔNG THỨC TỔNG HỢP
- Công thức chính
- Bảng diện tích đáy các hình đặc biệt
- IX. MẸO VÀ LƯU Ý
- 1. Các sai lầm thường gặp
- 2. Mẹo nhớ công thức
- 3. Thứ tự giải bài hình chóp
- 4. Cách nhận dạng nhanh
- X. KẾT LUẬN
I. GIỚI THIỆU VỀ HÌNH CHÓP
1. Định nghĩa hình chóp
Hình chóp là một khối đa diện có một mặt là đa giác (gọi là mặt đáy), các mặt còn lại là các tam giác có chung một đỉnh (gọi là đỉnh chóp).
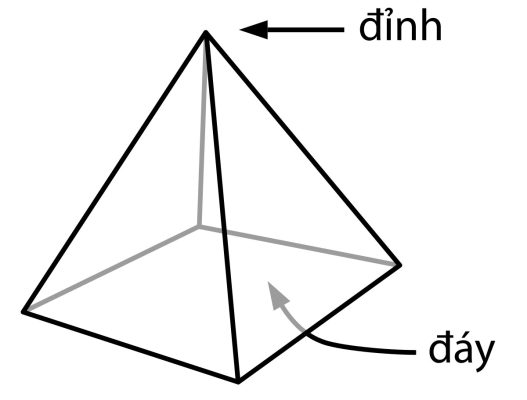
Ký hiệu: Hình chóp được ký hiệu theo đỉnh và các đỉnh của đáy.
- Ví dụ: Hình chóp $S.ABCD$ có đỉnh $S$ và đáy là tứ giác $ABCD$
- Hình chóp $S.ABC$ có đỉnh $S$ và đáy là tam giác $ABC$
Đặc điểm:
- Có một đỉnh duy nhất (đỉnh chóp)
- Tất cả các mặt bên đều là tam giác
- Các cạnh bên cùng xuất phát từ đỉnh chóp
2. Các yếu tố của hình chóp
Đỉnh chóp: Điểm $S$ – đỉnh chung của tất cả các mặt bên
Mặt đáy: Đa giác $ABCD…$ – mặt phẳng đối diện với đỉnh chóp
Các mặt bên: Các tam giác có chung đỉnh $S$
- Ví dụ: $SAB$, $SBC$, $SCD$, $SDA$
Các cạnh bên: Các đoạn thẳng nối đỉnh chóp với các đỉnh của đáy
- Ví dụ: $SA$, $SB$, $SC$, $SD$
Chiều cao (ký hiệu $h$): Khoảng cách từ đỉnh $S$ vuông góc xuống mặt phẳng đáy. Đây là yếu tố quan trọng nhất để tính thể tích.
3. Phân loại hình chóp
Theo đáy:
Hình chóp tam giác: Đáy là tam giác (3 cạnh)
- Có 4 mặt: 1 đáy + 3 mặt bên
- Có 4 đỉnh, 6 cạnh
Hình chóp tứ giác: Đáy là tứ giác (4 cạnh)
- Có 5 mặt: 1 đáy + 4 mặt bên
- Có 5 đỉnh, 8 cạnh
Hình chóp ngũ giác: Đáy là ngũ giác (5 cạnh)
- Có 6 mặt: 1 đáy + 5 mặt bên
- Có 6 đỉnh, 10 cạnh
Hình chóp n-giác: Đáy là đa giác $n$ cạnh
- Có $n+1$ mặt, $n+1$ đỉnh, $2n$ cạnh
Theo tính chất:
Hình chóp đều:
- Đáy là đa giác đều (tất cả các cạnh bằng nhau, các góc bằng nhau)
- Chân đường cao trùng với tâm của đáy
- Các cạnh bên bằng nhau
- Các mặt bên là các tam giác cân bằng nhau
Hình chóp đặc biệt:
- Hình chóp tam giác đều: Đáy là tam giác đều
- Hình chóp tứ giác đều: Đáy là hình vuông
- Hình chóp lục giác đều: Đáy là lục giác đều
II. CÔNG THỨC TỔNG QUÁT CỦA HÌNH CHÓP
1. Công thức thể tích khối chóp (QUAN TRỌNG NHẤT)
Đây là công thức quan trọng nhất và áp dụng cho MỌI loại hình chóp.
Công thức:
$$\boxed{V = \frac{1}{3} S_{\text{đáy}} \cdot h}$$
Trong đó:
- $V$: Thể tích khối chóp (đơn vị: cm³, m³, …)
- $S_{\text{đáy}}$: Diện tích mặt đáy
- $h$: Chiều cao (khoảng cách từ đỉnh vuông góc xuống mặt đáy)
Lưu ý quan trọng:
- Công thức này áp dụng cho MỌI hình chóp (tam giác, tứ giác, ngũ giác, đều hay không đều)
- Thể tích hình chóp bằng $\frac{1}{3}$ thể tích hình hộp hoặc hình lăng trụ có cùng đáy và chiều cao
- Luôn nhớ chia cho 3 – đây là sai lầm phổ biến nhất!
Ví dụ 1: Một hình chóp có diện tích đáy $S_{\text{đáy}} = 24$ cm² và chiều cao $h = 9$ cm. Tính thể tích.
Lời giải: $$V = \frac{1}{3} \times 24 \times 9 = \frac{216}{3} = 72 \text{ (cm}^3\text{)}$$
Kết luận: Thể tích khối chóp là 72 cm³.
2. Công thức diện tích toàn phần
Định nghĩa: Diện tích toàn phần là tổng diện tích tất cả các mặt của hình chóp.
Công thức:
$$\boxed{S_{tp} = S_{\text{đáy}} + S_{xq}}$$
Trong đó:
- $S_{tp}$: Diện tích toàn phần
- $S_{\text{đáy}}$: Diện tích mặt đáy
- $S_{xq}$: Diện tích xung quanh (tổng diện tích các mặt bên)
Với hình chóp đều:
Các mặt bên là các tam giác cân bằng nhau, nên:
$$S_{xq} = \frac{1}{2} \cdot P_{\text{đáy}} \cdot d$$
Trong đó:
- $P_{\text{đáy}}$: Chu vi đáy
- $d$: Trung đoạn (apothem) – chiều cao của mặt bên, kẻ từ đỉnh chóp vuông góc xuống cạnh đáy
Cách tính trung đoạn $d$:
Nếu biết chiều cao $h$ và khoảng cách từ tâm đáy đến giữa cạnh đáy $r$: $$d = \sqrt{h^2 + r^2}$$
3. Các công thức liên quan
Công thức tính chiều cao khi biết cạnh bên:
Nếu biết cạnh bên $SA$ và khoảng cách từ $A$ đến chân đường cao $H$:
$$\boxed{h = \sqrt{SA^2 – HA^2}}$$
Đây là ứng dụng trực tiếp của định lý Pythagore trong tam giác vuông $SHA$.
Công thức tính góc:
Góc giữa cạnh bên và mặt đáy:
Xét tam giác vuông tạo bởi cạnh bên, chiều cao và hình chiếu: $$\tan \alpha = \frac{h}{HA}$$
Trong đó $\alpha$ là góc giữa cạnh bên $SA$ và mặt đáy.
Góc giữa mặt bên và mặt đáy:
- Tìm giao tuyến của mặt bên với mặt đáy
- Kẻ đường vuông góc từ đỉnh chóp và từ chân đường cao xuống giao tuyến
- Góc tạo bởi hai đường vuông góc này chính là góc cần tìm
III. CÔNG THỨC HÌNH CHÓP TAM GIÁC ĐỀU
1. Định nghĩa
Hình chóp tam giác đều $S.ABC$ có các đặc điểm:
- Đáy $ABC$ là tam giác đều cạnh $a$
- Chân đường cao $H$ trùng với trọng tâm $G$ của tam giác đáy
- Các cạnh bên bằng nhau: $SA = SB = SC$
- Các mặt bên là các tam giác cân bằng nhau
2. Các công thức cơ bản
Diện tích đáy (tam giác đều cạnh $a$):
$$\boxed{S_{\text{đáy}} = \frac{a^2\sqrt{3}}{4}}$$
Cách nhớ: “a bình nhân căn 3 chia 4”
Bán kính đường tròn ngoại tiếp đáy:
$$\boxed{R = \frac{a}{\sqrt{3}} = \frac{a\sqrt{3}}{3}}$$
Đây là khoảng cách từ trọng tâm $G$ đến mỗi đỉnh $A$, $B$, $C$.
Khoảng cách từ đỉnh tam giác đến trọng tâm:
Trong tam giác đều, trọng tâm chia đường trung tuyến theo tỉ lệ 2:1. Nếu $M$ là trung điểm của $BC$:
- Đường trung tuyến: $AM = \frac{a\sqrt{3}}{2}$
- Khoảng cách: $AG = \frac{2}{3}AM = \frac{2}{3} \cdot \frac{a\sqrt{3}}{2} = \frac{a\sqrt{3}}{3}$
Chiều cao hình chóp (nếu biết cạnh bên $l$):
$$\boxed{h = \sqrt{l^2 – R^2} = \sqrt{l^2 – \frac{a^2}{3}}}$$
Chứng minh: Áp dụng định lý Pythagore cho tam giác vuông $SGA$: $$SG^2 + GA^2 = SA^2$$ $$h^2 + \frac{a^2}{3} = l^2$$
3. Công thức thể tích
$$\boxed{V = \frac{1}{3} \cdot \frac{a^2\sqrt{3}}{4} \cdot h = \frac{a^2h\sqrt{3}}{12}}$$
Ví dụ 2: Hình chóp tam giác đều có cạnh đáy $a = 6$ cm và cạnh bên $l = 5$ cm. Tính thể tích.
Lời giải:
Bước 1: Tính bán kính đường tròn ngoại tiếp: $$R = \frac{a\sqrt{3}}{3} = \frac{6\sqrt{3}}{3} = 2\sqrt{3} \text{ cm}$$
Bước 2: Tính chiều cao: $$h = \sqrt{l^2 – R^2} = \sqrt{25 – 12} = \sqrt{13} \text{ cm}$$
Bước 3: Tính diện tích đáy: $$S_{\text{đáy}} = \frac{36\sqrt{3}}{4} = 9\sqrt{3} \text{ cm}^2$$
Bước 4: Tính thể tích: $$V = \frac{1}{3} \times 9\sqrt{3} \times \sqrt{13} = 3\sqrt{3} \times \sqrt{13} = 3\sqrt{39} \text{ cm}^3$$
Kết luận: Thể tích là $3\sqrt{39}$ cm³ $\approx 18.73$ cm³.
4. Diện tích xung quanh
Trung đoạn (chiều cao của mặt bên):
Trung đoạn $d$ là đường cao của tam giác cân (mặt bên), kẻ từ $S$ xuống giữa cạnh đáy.
Nếu $M$ là trung điểm của $AB$: $$GM = \frac{a}{2\sqrt{3}} = \frac{a\sqrt{3}}{6}$$
Áp dụng định lý Pythagore trong tam giác $SGM$: $$d = \sqrt{h^2 + GM^2} = \sqrt{h^2 + \frac{a^2}{12}}$$
Diện tích xung quanh:
Hình chóp tam giác đều có 3 mặt bên giống nhau: $$S_{xq} = 3 \times \frac{1}{2} \times a \times d = \frac{3ad}{2}$$
Ví dụ 3: Tính diện tích xung quanh của hình chóp tam giác đều có cạnh đáy $a = 4$ cm và chiều cao $h = 3$ cm.
Lời giải:
Bước 1: Tính $GM$: $$GM = \frac{4\sqrt{3}}{6} = \frac{2\sqrt{3}}{3} \text{ cm}$$
Bước 2: Tính trung đoạn: $$d = \sqrt{9 + \frac{4}{3}} = \sqrt{\frac{31}{3}} = \frac{\sqrt{93}}{3} \text{ cm}$$
Bước 3: Tính diện tích xung quanh: $$S_{xq} = \frac{3 \times 4 \times \sqrt{93}/3}{2} = 2\sqrt{93} \text{ cm}^2 \approx 19.29 \text{ cm}^2$$
IV. CÔNG THỨC HÌNH CHÓP TỨ GIÁC ĐỀU
1. Định nghĩa
Hình chóp tứ giác đều $S.ABCD$ có các đặc điểm:
- Đáy $ABCD$ là hình vuông cạnh $a$
- Chân đường cao $O$ trùng với tâm hình vuông (giao điểm hai đường chéo)
- Các cạnh bên bằng nhau: $SA = SB = SC = SD$
- Các mặt bên là các tam giác cân bằng nhau
2. Các công thức cơ bản
Diện tích đáy (hình vuông cạnh $a$):
$$\boxed{S_{\text{đáy}} = a^2}$$
Đường chéo đáy:
$$\boxed{d_{\text{đáy}} = a\sqrt{2}}$$
Khoảng cách từ tâm đến đỉnh hình vuông:
Đây chính là nửa đường chéo: $$\boxed{OA = OB = OC = OD = \frac{a\sqrt{2}}{2}}$$
Chiều cao hình chóp (nếu biết cạnh bên $l$):
Áp dụng định lý Pythagore trong tam giác vuông $SOA$: $$\boxed{h = \sqrt{l^2 – OA^2} = \sqrt{l^2 – \frac{a^2}{2}}}$$
3. Công thức thể tích
$$\boxed{V = \frac{1}{3} \cdot a^2 \cdot h = \frac{a^2h}{3}}$$
Ví dụ 4: Hình chóp tứ giác đều có cạnh đáy $a = 8$ cm và chiều cao $h = 6$ cm. Tính thể tích.
Lời giải: $$V = \frac{a^2h}{3} = \frac{64 \times 6}{3} = \frac{384}{3} = 128 \text{ (cm}^3\text{)}$$
Kết luận: Thể tích là 128 cm³.
4. Diện tích xung quanh
Trung đoạn (chiều cao của mặt bên):
Nếu $M$ là trung điểm của $AB$: $$OM = \frac{a}{2}$$
Áp dụng định lý Pythagore trong tam giác $SOM$: $$d = \sqrt{h^2 + OM^2} = \sqrt{h^2 + \frac{a^2}{4}}$$
Diện tích xung quanh:
Hình chóp tứ giác đều có 4 mặt bên giống nhau: $$S_{xq} = 4 \times \frac{1}{2} \times a \times d = 2ad$$
Diện tích toàn phần:
$$\boxed{S_{tp} = a^2 + 2ad}$$
Ví dụ 5: Hình chóp tứ giác đều có cạnh đáy $a = 6$ cm và cạnh bên $l = 5$ cm. Tính diện tích toàn phần.
Lời giải:
Bước 1: Tính chiều cao: $$OA = \frac{6\sqrt{2}}{2} = 3\sqrt{2}$$ $$h = \sqrt{25 – 18} = \sqrt{7} \text{ cm}$$
Bước 2: Tính trung đoạn: $$d = \sqrt{7 + 9} = \sqrt{16} = 4 \text{ cm}$$
Bước 3: Tính diện tích xung quanh: $$S_{xq} = 2 \times 6 \times 4 = 48 \text{ cm}^2$$
Bước 4: Tính diện tích toàn phần: $$S_{tp} = 36 + 48 = 84 \text{ cm}^2$$
Kết luận: Diện tích toàn phần là 84 cm².
V. CÔNG THỨC HÌNH CHÓP ĐỀU TỔNG QUÁT
1. Hình chóp đều n-giác
Hình chóp đều có đáy là đa giác đều $n$ cạnh, mỗi cạnh có độ dài $a$.
Diện tích đáy:
Công thức 1 (dùng tang): $$S_{\text{đáy}} = \frac{na^2}{4\tan\frac{180°}{n}}$$
Công thức 2 (dùng bán kính ngoại tiếp $R$): $$S_{\text{đáy}} = \frac{n}{2}R^2\sin\frac{360°}{n}$$
Bán kính đường tròn ngoại tiếp:
$$R = \frac{a}{2\sin\frac{180°}{n}}$$
Thể tích:
$$\boxed{V = \frac{1}{3} S_{\text{đáy}} \cdot h}$$
Công thức vẫn giữ nguyên, chỉ cần tính đúng $S_{\text{đáy}}$ cho đa giác $n$ cạnh.
Diện tích xung quanh:
$$S_{xq} = n \times \frac{1}{2} \times a \times d = \frac{nad}{2}$$
Trong đó $d$ là trung đoạn (chiều cao mặt bên).
2. Bảng công thức nhanh cho các chóp đều
| Loại chóp | Đáy | $S_{\text{đáy}}$ | Khoảng cách $O$ đến đỉnh | Thể tích |
|---|---|---|---|---|
| Tam giác đều | Tam giác đều cạnh $a$ | $\frac{a^2\sqrt{3}}{4}$ | $\frac{a\sqrt{3}}{3}$ | $\frac{a^2h\sqrt{3}}{12}$ |
| Tứ giác đều | Hình vuông cạnh $a$ | $a^2$ | $\frac{a\sqrt{2}}{2}$ | $\frac{a^2h}{3}$ |
| Lục giác đều | Lục giác đều cạnh $a$ | $\frac{3a^2\sqrt{3}}{2}$ | $a$ | $\frac{a^2h\sqrt{3}}{2}$ |
Lưu ý đặc biệt:
- Lục giác đều có tính chất: $R = a$ (bán kính ngoại tiếp bằng cạnh)
- Diện tích lục giác đều = 6 × diện tích tam giác đều cạnh $a$
VI. CÔNG THỨC HÌNH CHÓP CỤT
1. Định nghĩa hình chóp cụt
Hình chóp cụt là phần của hình chóp nằm giữa mặt đáy và một mặt phẳng song song với đáy cắt hình chóp.
Các yếu tố:
- Hai đáy: Đáy lớn (diện tích $S_1$) và đáy nhỏ (diện tích $S_2$)
- Chiều cao $h$: Khoảng cách vuông góc giữa hai mặt đáy
- Các mặt bên: Là các hình thang (nếu chóp cụt đều thì là các hình thang cân)
- Các cạnh bên: Các đoạn thẳng nối các đỉnh tương ứng của hai đáy
2. Công thức thể tích hình chóp cụt
Đây là công thức quan trọng nhất của hình chóp cụt:
$$\boxed{V = \frac{h}{3}(S_1 + S_2 + \sqrt{S_1 \cdot S_2})}$$
Trong đó:
- $h$: Chiều cao chóp cụt (khoảng cách giữa hai đáy)
- $S_1$: Diện tích đáy lớn
- $S_2$: Diện tích đáy nhỏ
- $\sqrt{S_1 \cdot S_2}$: Trung bình nhân của hai diện tích
Cách nhớ: “h chia 3, ngoặc S1 cộng S2 cộng căn S1 nhân S2”
Ví dụ 6: Hình chóp cụt có đáy lớn $S_1 = 36$ cm², đáy nhỏ $S_2 = 16$ cm², chiều cao $h = 6$ cm. Tính thể tích.
Lời giải:
Bước 1: Tính căn bậc hai của tích hai diện tích: $$\sqrt{S_1 \cdot S_2} = \sqrt{36 \times 16} = \sqrt{576} = 24$$
Bước 2: Áp dụng công thức: $$V = \frac{6}{3}(36 + 16 + 24)$$ $$= 2 \times 76 = 152 \text{ (cm}^3\text{)}$$
Kết luận: Thể tích là 152 cm³.
3. Công thức chóp cụt tứ giác đều
Khi đáy lớn là hình vuông cạnh $a_1$ và đáy nhỏ là hình vuông cạnh $a_2$:
Thể tích: $$\boxed{V = \frac{h}{3}(a_1^2 + a_2^2 + a_1a_2)}$$
Ví dụ 7: Hình chóp cụt tứ giác đều có cạnh đáy lớn $a_1 = 8$ cm, cạnh đáy nhỏ $a_2 = 4$ cm, chiều cao $h = 6$ cm. Tính thể tích.
Lời giải:
Bước 1: Tính các diện tích:
- $a_1^2 = 64$
- $a_2^2 = 16$
- $a_1a_2 = 32$
Bước 2: Áp dụng công thức: $$V = \frac{6}{3}(64 + 16 + 32)$$ $$= 2 \times 112 = 224 \text{ (cm}^3\text{)}$$
Kết luận: Thể tích là 224 cm³.
4. Diện tích xung quanh chóp cụt đều
Với chóp cụt $n$-giác đều:
$$\boxed{S_{xq} = \frac{n(a_1 + a_2)d}{2}}$$
Trong đó:
- $n$: Số cạnh đáy
- $a_1, a_2$: Cạnh đáy lớn, đáy nhỏ
- $d$: Trung đoạn (chiều cao của mặt bên hình thang)
Trung đoạn của chóp cụt tứ giác đều:
Nếu $O_1$, $O_2$ là tâm hai đáy và $M_1$, $M_2$ là trung điểm cạnh tương ứng: $$O_1M_1 = \frac{a_1}{2}, \quad O_2M_2 = \frac{a_2}{2}$$
$$d = \sqrt{h^2 + (O_1M_1 – O_2M_2)^2} = \sqrt{h^2 + \left(\frac{a_1 – a_2}{2}\right)^2}$$
5. Mối liên hệ với hình chóp ban đầu
Khi cắt hình chóp bằng mặt phẳng song song với đáy, ta được hình chóp cụt và hình chóp nhỏ phía trên.
Tỷ số đồng dạng:
Nếu hình chóp ban đầu có chiều cao $H$ và cắt ở vị trí cách đỉnh $h_1$: $$k = \frac{h_1}{H}$$
Mối liên hệ diện tích:
Hai đáy đồng dạng với tỷ số: $$\frac{S_2}{S_1} = k^2$$
Thể tích chóp cụt:
$$V_{\text{cụt}} = V_{\text{toàn}} – V_{\text{nhỏ}} = V_{\text{toàn}}(1 – k^3)$$
Ví dụ: Hình chóp có $V = 270$ cm³. Cắt tại vị trí $\frac{1}{3}$ chiều cao tính từ đỉnh. Tính thể tích chóp cụt.
Lời giải:
- $k = \frac{1}{3}$
- $V_{\text{nhỏ}} = 270 \times \left(\frac{1}{3}\right)^3 = 270 \times \frac{1}{27} = 10$ cm³
- $V_{\text{cụt}} = 270 – 10 = 260$ cm³
VII. CÁC DẠNG BÀI TẬP TRỌNG TÂM
Dạng 1: Tính thể tích khi biết diện tích đáy và chiều cao
Phương pháp: Áp dụng trực tiếp công thức $V = \frac{1}{3}S_{\text{đáy}} \cdot h$
Ví dụ 8: Hình chóp có đáy là tam giác vuông với các cạnh góc vuông là 6 cm và 8 cm, chiều cao của hình chóp là 10 cm. Tính thể tích.
Lời giải:
Bước 1: Tính diện tích đáy (tam giác vuông): $$S_{\text{đáy}} = \frac{1}{2} \times 6 \times 8 = 24 \text{ cm}^2$$
Bước 2: Tính thể tích: $$V = \frac{1}{3} \times 24 \times 10 = 80 \text{ cm}^3$$
Kết luận: Thể tích là 80 cm³.
Dạng 2: Tính chiều cao khi biết thể tích và đáy
Phương pháp: Từ $V = \frac{1}{3}S_{\text{đáy}} \cdot h$ suy ra: $$h = \frac{3V}{S_{\text{đáy}}}$$
Ví dụ: Hình chóp có thể tích 120 cm³ và diện tích đáy 45 cm². Tính chiều cao.
Lời giải: $$h = \frac{3 \times 120}{45} = \frac{360}{45} = 8 \text{ cm}$$
Dạng 3: Hình chóp có các mặt bên vuông góc với đáy
Đặc điểm: Một hoặc nhiều mặt bên vuông góc với mặt đáy.
Phương pháp:
- Xác định cạnh bên vuông góc với đáy → đó chính là chiều cao
- Tính diện tích đáy từ các cạnh còn lại
- Áp dụng công thức thể tích
Ví dụ: Hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B$ với $AB = 3$ cm, $BC = 4$ cm. Cạnh $SB$ vuông góc với đáy và $SB = 5$ cm. Tính thể tích.
Lời giải:
- Chiều cao: $h = SB = 5$ cm (vì $SB \perp$ đáy)
- Diện tích đáy: $S = \frac{1}{2} \times 3 \times 4 = 6$ cm²
- Thể tích: $V = \frac{1}{3} \times 6 \times 5 = 10$ cm³
Dạng 4: Tính tỷ số thể tích
Nguyên lý: Khi chia hình chóp thành các phần, tỷ số thể tích bằng tích các tỷ số cạnh tương ứng.
Ví dụ 9: Cho hình chóp $S.ABC$. Gọi $M$, $N$ lần lượt là trung điểm của $SA$ và $SB$. Tính tỷ số $\frac{V_{S.MNC}}{V_{S.ABC}}$.
Phương pháp:
Áp dụng công thức tỷ số thể tích: $$\frac{V_{S.MNC}}{V_{S.ABC}} = \frac{SM}{SA} \times \frac{SN}{SB} \times \frac{SC}{SC}$$
Lời giải: $$\frac{V_{S.MNC}}{V_{S.ABC}} = \frac{1}{2} \times \frac{1}{2} \times 1 = \frac{1}{4}$$
Kết luận: Thể tích $V_{S.MNC} = \frac{1}{4}V_{S.ABC}$.
Dạng 5: Hình chóp đều – Tính các yếu tố khi biết góc
Ví dụ 10: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy $a$, cạnh bên tạo với mặt đáy góc $60°$. Tính thể tích theo $a$.
Lời giải:
Bước 1: Xác định góc
Góc giữa cạnh bên $SA$ và mặt đáy là góc $\widehat{SAO} = 60°$ (với $O$ là tâm đáy).
Bước 2: Tính $OA$ $$OA = \frac{a\sqrt{2}}{2}$$
Bước 3: Tính chiều cao $$\tan 60° = \frac{SO}{OA}$$ $$\sqrt{3} = \frac{h}{a\sqrt{2}/2}$$ $$h = \frac{a\sqrt{6}}{2}$$
Bước 4: Tính thể tích $$V = \frac{1}{3} \times a^2 \times \frac{a\sqrt{6}}{2} = \frac{a^3\sqrt{6}}{6}$$
Kết luận: Thể tích là $\frac{a^3\sqrt{6}}{6}$ (đơn vị khối).
Dạng 6: Khoảng cách và góc trong hình chóp
Các bài toán thường gặp:
- Khoảng cách từ điểm đến mặt phẳng:
- Kẻ đường vuông góc từ điểm đến mặt phẳng
- Tính độ dài đoạn vuông góc đó
- Góc giữa đường thẳng và mặt phẳng:
- Tìm hình chiếu của đường thẳng lên mặt phẳng
- Góc giữa đường thẳng và hình chiếu là góc cần tìm
- Góc giữa hai mặt phẳng:
- Tìm giao tuyến của hai mặt phẳng
- Kẻ hai đường vuông góc với giao tuyến từ hai mặt phẳng
- Góc tạo bởi hai đường đó là góc cần tìm
VIII. BẢNG CÔNG THỨC TỔNG HỢP
Công thức chính
| Nội dung | Công thức | Ghi chú |
|---|---|---|
| Thể tích (tổng quát) | $V = \frac{1}{3}S_{\text{đáy}} \cdot h$ | Áp dụng cho mọi hình chóp |
| Diện tích toàn phần | $S_{tp} = S_{\text{đáy}} + S_{xq}$ | Tổng đáy và xung quanh |
| Chóp tam giác đều | $S_{\text{đáy}} = \frac{a^2\sqrt{3}}{4}$ | Đáy là tam giác đều |
| Chóp tứ giác đều | $S_{\text{đáy}} = a^2$ | Đáy là hình vuông |
| Chiều cao (biết cạnh bên) | $h = \sqrt{l^2 – R^2}$ | $R$: khoảng cách tâm-đỉnh |
| Thể tích chóp cụt | $V = \frac{h}{3}(S_1 + S_2 + \sqrt{S_1S_2})$ | $S_1$: đáy lớn, $S_2$: đáy nhỏ |
| Diện tích xung quanh (đều) | $S_{xq} = \frac{P \cdot d}{2}$ | $P$: chu vi, $d$: trung đoạn |
Bảng diện tích đáy các hình đặc biệt
| Hình dạng đáy | Công thức diện tích | Ghi chú |
|---|---|---|
| Tam giác vuông | $S = \frac{1}{2}ab$ | $a$, $b$: cạnh góc vuông |
| Tam giác thường | $S = \frac{1}{2}ah$ | $a$: đáy, $h$: đường cao |
| Tam giác đều cạnh $a$ | $S = \frac{a^2\sqrt{3}}{4}$ | Công thức quan trọng |
| Hình vuông cạnh $a$ | $S = a^2$ | Đơn giản nhất |
| Hình chữ nhật | $S = ab$ | $a$: dài, $b$: rộng |
| Hình thoi | $S = \frac{1}{2}d_1d_2$ | $d_1$, $d_2$: đường chéo |
| Hình thang | $S = \frac{(a+b)h}{2}$ | $a$, $b$: đáy, $h$: cao |
| Lục giác đều cạnh $a$ | $S = \frac{3a^2\sqrt{3}}{2}$ | Bằng 6 tam giác đều |
IX. MẸO VÀ LƯU Ý
1. Các sai lầm thường gặp
❌ SAI LẦM 1: Quên chia 3 trong công thức thể tích
Sai:
- $V = S_{\text{đáy}} \cdot h$ ❌
Đúng:
- $V = \frac{1}{3}S_{\text{đáy}} \cdot h$ ✓
Lời khuyên: Luôn nhớ “một phần ba” – đây là sai lầm phổ biến nhất!
❌ SAI LẦM 2: Nhầm lẫn giữa chiều cao hình chóp và trung đoạn
Chiều cao $h$:
- Khoảng cách từ đỉnh vuông góc xuống mặt đáy
- Dùng để tính thể tích
Trung đoạn $d$:
- Chiều cao của mặt bên (tam giác)
- Kẻ từ đỉnh xuống giữa cạnh đáy
- Dùng để tính diện tích xung quanh
❌ SAI LẦM 3: Tính sai diện tích đáy
Phải phân biệt:
- Tam giác vuông: $S = \frac{1}{2}ab$
- Tam giác đều: $S = \frac{a^2\sqrt{3}}{4}$
- Tam giác thường: $S = \frac{1}{2}ah$ hoặc dùng công thức Heron
❌ SAI LẦM 4: Quên $\sqrt{S_1 \cdot S_2}$ trong công thức chóp cụt
Sai:
- $V = \frac{h}{3}(S_1 + S_2)$ ❌
Đúng:
- $V = \frac{h}{3}(S_1 + S_2 + \sqrt{S_1 \cdot S_2})$ ✓
2. Mẹo nhớ công thức
Mẹo 1: Thể tích hình chóp
“Một phần ba đáy nhân cao”
$$V = \frac{1}{3}S_{\text{đáy}} \cdot h$$
Mẹo 2: Tam giác đều
“a bình nhân căn 3 chia 4”
$$S = \frac{a^2\sqrt{3}}{4}$$
Mẹo 3: Chóp cụt
“h trên 3, ngoặc S1 cộng S2 cộng căn S1 nhân S2”
$$V = \frac{h}{3}(S_1 + S_2 + \sqrt{S_1S_2})$$
Mẹo 4: Khoảng cách trong chóp đều
- Tam giác đều: $R = \frac{a\sqrt{3}}{3}$ (chia 3)
- Tứ giác đều: $R = \frac{a\sqrt{2}}{2}$ (chia 2)
- Lục giác đều: $R = a$ (bằng cạnh)
3. Thứ tự giải bài hình chóp
Bước 1: Vẽ hình và đánh dấu
- Vẽ hình chóp với các yếu tố đã cho
- Đánh dấu rõ đỉnh, đáy, chiều cao
- Đánh dấu các yếu tố đặc biệt (góc, khoảng cách…)
Bước 2: Xác định loại chóp
- Hình chóp đều? Tam giác? Tứ giác?
- Đáy có hình dạng gì?
- Các tính chất đặc biệt?
Bước 3: Tính diện tích đáy
- Xác định hình dạng đáy (tam giác, tứ giác, …)
- Áp dụng công thức phù hợp
- Kiểm tra đơn vị
Bước 4: Tìm chiều cao
- Từ điều kiện bài toán (cạnh bên, góc, …)
- Dùng định lý Pythagore nếu cần
- Chú ý: chiều cao vuông góc với đáy
Bước 5: Áp dụng công thức
- Thể tích: $V = \frac{1}{3}S_{\text{đáy}} \cdot h$
- Diện tích: $S_{tp} = S_{\text{đáy}} + S_{xq}$
Bước 6: Kiểm tra
- Đơn vị có đúng không?
- Kết quả có hợp lý không?
- So với đáp án (nếu có)
4. Cách nhận dạng nhanh
“Hình chóp đều” →
- Đáy là đa giác đều
- Chân đường cao trùng tâm đáy
- Các cạnh bên bằng nhau
“Tam giác đều” →
- Dùng công thức $S = \frac{a^2\sqrt{3}}{4}$
- Khoảng cách tâm-đỉnh: $R = \frac{a\sqrt{3}}{3}$
“Tứ giác đều” →
- Đáy là hình vuông: $S = a^2$
- Khoảng cách tâm-đỉnh: $R = \frac{a\sqrt{2}}{2}$
“Chóp cụt” →
- Có 2 đáy song song
- Dùng công thức riêng có $\sqrt{S_1S_2}$
X. KẾT LUẬN
Bài viết đã hệ thống hóa đầy đủ và chi tiết các công thức về hình chóp:
Công thức tổng quát áp dụng cho mọi hình chóp:
- Thể tích: $V = \frac{1}{3}S_{\text{đáy}} \cdot h$
- Diện tích toàn phần: $S_{tp} = S_{\text{đáy}} + S_{xq}$
Công thức hình chóp tam giác đều:
- Diện tích đáy: $S = \frac{a^2\sqrt{3}}{4}$
- Khoảng cách tâm-đỉnh: $R = \frac{a\sqrt{3}}{3}$
- Chiều cao: $h = \sqrt{l^2 – \frac{a^2}{3}}$
Công thức hình chóp tứ giác đều:
- Diện tích đáy: $S = a^2$
- Khoảng cách tâm-đỉnh: $R = \frac{a\sqrt{2}}{2}$
- Chiều cao: $h = \sqrt{l^2 – \frac{a^2}{2}}$
Công thức hình chóp đều $n$-giác – tổng quát hóa
Công thức hình chóp cụt:
- Thể tích: $V = \frac{h}{3}(S_1 + S_2 + \sqrt{S_1S_2})$
- Diện tích xung quanh: $S_{xq} = \frac{n(a_1+a_2)d}{2}$
6 dạng bài tập trọng tâm với phương pháp giải chi tiết
Bảng công thức tra cứu nhanh – tiện lợi cho ôn tập
Mẹo nhớ và cảnh báo sai lầm – giúp tránh nhầm lẫn
Xem thêm các bài liên quan:
- [Công thức hình lăng trụ – Thể tích và diện tích]
- [Công thức hình nón – Đầy đủ và chi tiết]
- [Công thức hình trụ – Công thức cơ bản đến nâng cao]
- [Công thức hình cầu – Diện tích và thể tích]

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
