Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. Giới Thiệu Về Hình Hộp Chữ Nhật
- 1. Định nghĩa hình hộp chữ nhật
- 2. Các yếu tố của hình hộp chữ nhật
- 3. Tính chất hình hộp chữ nhật
- 4. Phân biệt hình hộp chữ nhật và hình lập phương
- II. Công Thức Diện Tích Đáy
- 1. Định nghĩa
- 2. Công thức
- 3. Công thức chu vi đáy
- 4. Ví dụ minh họa
- III. Công Thức Diện Tích Xung Quanh
- 1. Định nghĩa
- 2. Công thức
- 3. Cách nhớ
- 4. Các công thức suy ra
- 5. Ví dụ minh họa
- IV. Công Thức Diện Tích Toàn Phần
- 1. Định nghĩa
- 2. Công thức
- 3. Cách nhớ
- 4. Mối quan hệ giữa các diện tích
- 5. Ví dụ minh họa
- V. Công Thức Thể Tích
- 1. Định nghĩa
- 2. Công thức
- 3. Cách nhớ
- 4. Đơn vị thể tích và quy đổi
- 5. Các công thức suy ra
- 6. Ví dụ minh họa
- VI. Công Thức Đường Chéo
- 1. Đường chéo mặt
- 2. Đường chéo hình hộp
- 3. Ví dụ minh họa
- VII. Bảng Tổng Hợp Công Thức
- Bảng 1: Công thức cơ bản
- Bảng 2: Công thức tính chiều cao
- Bảng 3: Mối quan hệ công thức
- Bảng 4: Quy đổi đơn vị
- VIII. Các Dạng Bài Tập Thường Gặp
- Dạng 1: Tính diện tích, thể tích khi biết 3 kích thước
- Dạng 2: Tính chiều cao khi biết thể tích
- Dạng 3: Tính chi phí sơn, dán
- Dạng 4: Bài toán đổ nước vào bể
- Dạng 5: Tính kích thước khi biết thể tích và tỉ lệ
- Dạng 6: Tăng/giảm kích thước
- IX. Bài Tập Thực Tế Vận Dụng
- X. Kết Luận
- Tổng kết công thức
- Lưu ý quan trọng
I. Giới Thiệu Về Hình Hộp Chữ Nhật
1. Định nghĩa hình hộp chữ nhật
Định nghĩa: Hình hộp chữ nhật là một khối đa diện có 6 mặt đều là hình chữ nhật. Đây là một trong những hình khối cơ bản và phổ biến nhất trong hình học không gian.
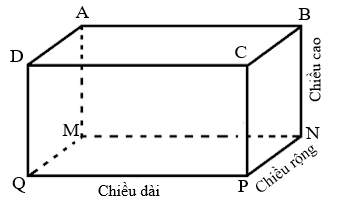
Đặc điểm nhận biết:
- Có 8 đỉnh
- Có 12 cạnh
- Có 6 mặt (tất cả đều là hình chữ nhật)
- Các mặt đối diện song song và bằng nhau
2. Các yếu tố của hình hộp chữ nhật
a) Chiều dài (a):
- Cạnh dài nhất của mặt đáy
- Thường ký hiệu là a hoặc l
- Đơn vị: cm, m, dm…
b) Chiều rộng (b):
- Cạnh ngắn hơn của mặt đáy
- Thường ký hiệu là b hoặc w
- Đơn vị: cm, m, dm…
c) Chiều cao (h hoặc c):
- Độ cao từ mặt đáy lên đỉnh
- Thường ký hiệu là h (height) hoặc c
- Đơn vị: cm, m, dm…
d) Đáy:
- 2 mặt hình chữ nhật đối diện
- Mặt đáy dưới và mặt đáy trên
- Kích thước: a × b
e) Mặt bên:
- 4 mặt hình chữ nhật xung quanh
- 2 mặt kích thước a × h
- 2 mặt kích thước b × h
3. Tính chất hình hộp chữ nhật
Về mặt:
- 6 mặt đều là hình chữ nhật
- Các mặt đối diện song song và bằng nhau
- 3 cặp mặt: 2 đáy, 2 mặt (a×h), 2 mặt (b×h)
Về cạnh:
- 12 cạnh chia thành 3 nhóm:
- 4 cạnh dài = a
- 4 cạnh rộng = b
- 4 cạnh cao = h
- Các cạnh song song thì bằng nhau
Về đường chéo:
- Có 4 đường chéo của hình hộp
- Tất cả đường chéo đều bằng nhau
- Các đường chéo cắt nhau tại trung điểm
Về tâm đối xứng:
- Có tâm đối xứng tại giao điểm các đường chéo
4. Phân biệt hình hộp chữ nhật và hình lập phương
| Đặc điểm | Hình hộp chữ nhật | Hình lập phương |
|---|---|---|
| Kích thước | $a \neq b \neq h$ | $a = b = h$ |
| Số mặt | 6 mặt hình chữ nhật | 6 mặt hình vuông |
| Công thức V | $V = a \times b \times h$ | $V = a^3$ |
| Mối quan hệ | Hình tổng quát | Trường hợp đặc biệt |
Kết luận: Hình lập phương là trường hợp đặc biệt của hình hộp chữ nhật khi $a = b = h$
II. Công Thức Diện Tích Đáy
1. Định nghĩa
Diện tích đáy là diện tích của mặt đáy (mặt hình chữ nhật phía dưới hoặc phía trên).
Lưu ý:
- Hình hộp có 2 mặt đáy giống nhau
- Mặt đáy dưới và mặt đáy trên có diện tích bằng nhau
2. Công thức
$$S_{\text{đáy}} = a \times b$$
Trong đó:
- $S_{\text{đáy}}$: Diện tích một mặt đáy
- $a$: Chiều dài mặt đáy
- $b$: Chiều rộng mặt đáy
Đơn vị: cm², m², dm², km²…
3. Công thức chu vi đáy
$$P_{\text{đáy}} = 2(a + b)$$
Trong đó:
- $P_{\text{đáy}}$: Chu vi mặt đáy
- $a$: Chiều dài
- $b$: Chiều rộng
Ứng dụng: Chu vi đáy được dùng để tính diện tích xung quanh
4. Ví dụ minh họa
Ví dụ 1: Hình hộp chữ nhật có chiều dài 8cm, chiều rộng 5cm. Tính diện tích và chu vi đáy.
Lời giải:
- Diện tích đáy: $$S_{\text{đáy}} = 8 \times 5 = 40 \text{ cm}^2$$
- Chu vi đáy: $$P_{\text{đáy}} = 2(8 + 5) = 26 \text{ cm}$$
Đáp án: $S_{\text{đáy}} = 40$ cm², $P_{\text{đáy}} = 26$ cm
Ví dụ 2: Mặt đáy hình hộp có diện tích 56cm², chiều dài 8cm. Tính chiều rộng.
Lời giải:
$$b = \frac{S_{\text{đáy}}}{a} = \frac{56}{8} = 7 \text{ cm}$$
Đáp án: b = 7 cm
Ví dụ 3: Hộp có đáy hình vuông cạnh 6cm. Tính diện tích đáy.
Lời giải:
$$S_{\text{đáy}} = 6 \times 6 = 36 \text{ cm}^2$$
Đáp án: $S_{\text{đáy}} = 36$ cm²
III. Công Thức Diện Tích Xung Quanh
1. Định nghĩa
Diện tích xung quanh là tổng diện tích của 4 mặt bên (không tính 2 mặt đáy).
4 mặt bên bao gồm:
- 2 mặt có kích thước: a × h
- 2 mặt có kích thước: b × h
2. Công thức
$$S_{xq} = 2(a + b) \times h = P_{\text{đáy}} \times h$$
Hoặc viết chi tiết:
$$S_{xq} = 2ah + 2bh = 2h(a + b)$$
Trong đó:
- $S_{xq}$: Diện tích xung quanh
- $a$: Chiều dài đáy
- $b$: Chiều rộng đáy
- $h$: Chiều cao
- $P_{\text{đáy}} = 2(a + b)$: Chu vi đáy
Đơn vị: cm², m², dm²…
3. Cách nhớ
Diện tích xung quanh = Chu vi đáy × Chiều cao
$$S_{xq} = P_{\text{đáy}} \times h$$
4. Các công thức suy ra
a) Tính chiều cao khi biết diện tích xung quanh:
$$h = \frac{S_{xq}}{2(a + b)} = \frac{S_{xq}}{P_{\text{đáy}}}$$
b) Tính chu vi đáy khi biết diện tích xung quanh:
$$P_{\text{đáy}} = \frac{S_{xq}}{h}$$
c) Tính chiều dài hoặc chiều rộng:
Từ $P_{\text{đáy}} = 2(a + b)$ và $S_{xq} = P_{\text{đáy}} \times h$, ta có thể tính được $a$ hoặc $b$ nếu biết các đại lượng khác.
5. Ví dụ minh họa
Ví dụ 1: Hình hộp có chiều dài 10cm, chiều rộng 6cm, chiều cao 4cm. Tính diện tích xung quanh.
Lời giải:
$$S_{xq} = 2(10 + 6) \times 4 = 2 \times 16 \times 4 = 128 \text{ cm}^2$$
Đáp án: $S_{xq} = 128$ cm²
Ví dụ 2: Hình hộp có diện tích xung quanh 200cm², chu vi đáy 20cm. Tính chiều cao.
Lời giải:
$$h = \frac{S_{xq}}{P_{\text{đáy}}} = \frac{200}{20} = 10 \text{ cm}$$
Đáp án: h = 10 cm
Ví dụ 3: Bể cá có chiều dài 50cm, chiều rộng 30cm, chiều cao 40cm. Tính diện tích kính làm bể (không tính nắp).
Lời giải:
Diện tích kính = Diện tích xung quanh + Diện tích đáy
- Diện tích xung quanh: $$S_{xq} = 2(50 + 30) \times 40 = 6,400 \text{ cm}^2$$
- Diện tích đáy: $$S_{\text{đáy}} = 50 \times 30 = 1,500 \text{ cm}^2$$
- Tổng: $$S = 6,400 + 1,500 = 7,900 \text{ cm}^2$$
Đáp án: 7,900 cm²
Ví dụ 4: Phòng dài 8m, rộng 6m, cao 3m. Tính diện tích 4 bức tường (không tính sàn và trần).
Lời giải:
$$S_{xq} = 2(8 + 6) \times 3 = 2 \times 14 \times 3 = 84 \text{ m}^2$$
Đáp án: 84 m²
IV. Công Thức Diện Tích Toàn Phần
1. Định nghĩa
Diện tích toàn phần là tổng diện tích của tất cả 6 mặt của hình hộp chữ nhật.
Bao gồm:
- 4 mặt bên (diện tích xung quanh)
- 2 mặt đáy (trên và dưới)
2. Công thức
$$S_{tp} = S_{xq} + 2S_{\text{đáy}}$$
Hoặc viết đầy đủ:
$$S_{tp} = 2(a + b)h + 2ab$$
Hoặc dạng rút gọn:
$$S_{tp} = 2(ab + ah + bh)$$
Trong đó:
- $S_{tp}$: Diện tích toàn phần
- $S_{xq}$: Diện tích xung quanh
- $S_{\text{đáy}}$: Diện tích một mặt đáy
Đơn vị: cm², m², dm²…
3. Cách nhớ
Diện tích toàn phần = Diện tích xung quanh + 2 × Diện tích đáy
$$S_{tp} = S_{xq} + 2S_{\text{đáy}}$$
4. Mối quan hệ giữa các diện tích
Từ công thức trên, ta có:
$$S_{tp} = S_{xq} + 2S_{\text{đáy}}$$
$$S_{xq} = S_{tp} – 2S_{\text{đáy}}$$
$$S_{\text{đáy}} = \frac{S_{tp} – S_{xq}}{2}$$
5. Ví dụ minh họa
Ví dụ 1: Hình hộp có $a = 8$cm, $b = 5$cm, $h = 6$cm. Tính diện tích toàn phần.
Lời giải:
Cách 1: Tính qua $S_{xq}$ và $S_{\text{đáy}}$
- Diện tích đáy: $$S_{\text{đáy}} = 8 \times 5 = 40 \text{ cm}^2$$
- Diện tích xung quanh: $$S_{xq} = 2(8 + 5) \times 6 = 156 \text{ cm}^2$$
- Diện tích toàn phần: $$S_{tp} = 156 + 2 \times 40 = 236 \text{ cm}^2$$
Đáp án: $S_{tp} = 236$ cm²
Ví dụ 2: Cách 2 – Dùng công thức trực tiếp:
$$S_{tp} = 2(8 \times 5 + 8 \times 6 + 5 \times 6)$$
$$S_{tp} = 2(40 + 48 + 30) = 2 \times 118 = 236 \text{ cm}^2$$
Đáp án: $S_{tp} = 236$ cm²
Ví dụ 3: Hộp quà có kích thước 25cm × 15cm × 10cm. Tính diện tích giấy cần để bọc hộp.
Lời giải:
$$S_{tp} = 2(25 \times 15 + 25 \times 10 + 15 \times 10)$$
$$S_{tp} = 2(375 + 250 + 150) = 2 \times 775 = 1,550 \text{ cm}^2$$
Đáp án: 1,550 cm²
Ví dụ 4: Hình hộp có diện tích toàn phần 280cm², diện tích xung quanh 200cm². Tính diện tích một mặt đáy.
Lời giải:
$$S_{\text{đáy}} = \frac{S_{tp} – S_{xq}}{2} = \frac{280 – 200}{2} = 40 \text{ cm}^2$$
Đáp án: $S_{\text{đáy}} = 40$ cm²
V. Công Thức Thể Tích
1. Định nghĩa
Thể tích là số đo phần không gian mà hình hộp chữ nhật chiếm chỗ.
Đơn vị đo: cm³, m³, dm³, lít, ml…
2. Công thức
$$V = a \times b \times h = S_{\text{đáy}} \times h$$
Trong đó:
- $V$: Thể tích
- $a$: Chiều dài
- $b$: Chiều rộng
- $h$: Chiều cao
- $S_{\text{đáy}} = a \times b$: Diện tích đáy
Đơn vị: cm³, m³, dm³, lít…
3. Cách nhớ
Thể tích = Dài × Rộng × Cao = Diện tích đáy × Cao
$$V = a \times b \times h = S_{\text{đáy}} \times h$$
4. Đơn vị thể tích và quy đổi
Bảng quy đổi thể tích:
| Đơn vị | Quy đổi |
|---|---|
| 1 m³ | = 1,000 dm³ = 1,000,000 cm³ |
| 1 dm³ | = 1 lít = 1,000 cm³ |
| 1 cm³ | = 1 ml (mililít) |
| 1 lít | = 1 dm³ = 1,000 ml |
Lưu ý quan trọng:
- 1 dm³ = 1 lít (thường dùng cho bài toán nước)
- 1 m³ = 1,000 lít
5. Các công thức suy ra
a) Tính chiều cao khi biết thể tích:
$$h = \frac{V}{a \times b} = \frac{V}{S_{\text{đáy}}}$$
b) Tính chiều dài:
$$a = \frac{V}{b \times h}$$
c) Tính chiều rộng:
$$b = \frac{V}{a \times h}$$
d) Tính diện tích đáy:
$$S_{\text{đáy}} = \frac{V}{h}$$
6. Ví dụ minh họa
Ví dụ 1: Bể nước hình hộp chữ nhật dài 2m, rộng 1.5m, cao 1.2m. Tính thể tích bể (đơn vị lít).
Lời giải:
- Thể tích: $$V = 2 \times 1.5 \times 1.2 = 3.6 \text{ m}^3$$
- Đổi sang lít: $$3.6 \text{ m}^3 = 3,600 \text{ lít}$$
Đáp án: 3,600 lít
Ví dụ 2: Thùng chứa có thể tích 240 lít, đáy hình chữ nhật 60cm × 40cm. Tính chiều cao.
Lời giải:
- Đổi đơn vị: 240 lít = 240 dm³
- Đổi đáy: 60cm × 40cm = 6dm × 4dm
- Chiều cao:
$$h = \frac{V}{S_{\text{đáy}}} = \frac{240}{6 \times 4} = \frac{240}{24} = 10 \text{ dm}$$
Đáp án: h = 10 dm = 1 m
Ví dụ 3: Hộp sữa hình hộp chữ nhật có thể tích 1 lít, đáy hình vuông cạnh 8cm. Tính chiều cao.
Lời giải:
- Đổi: 1 lít = 1,000 cm³
- Diện tích đáy: $8 \times 8 = 64$ cm²
- Chiều cao:
$$h = \frac{1,000}{64} = 15.625 \text{ cm}$$
Đáp án: h ≈ 15.6 cm
Ví dụ 4: Container dài 6m, rộng 2.4m, cao 2.6m. Tính thể tích chứa hàng (m³).
Lời giải:
$$V = 6 \times 2.4 \times 2.6 = 37.44 \text{ m}^3$$
Đáp án: V = 37.44 m³
VI. Công Thức Đường Chéo
1. Đường chéo mặt
a) Đường chéo của mặt đáy:
$$d_{\text{đáy}} = \sqrt{a^2 + b^2}$$
b) Đường chéo của mặt bên (a × h):
$$d_1 = \sqrt{a^2 + h^2}$$
c) Đường chéo của mặt bên (b × h):
$$d_2 = \sqrt{b^2 + h^2}$$
2. Đường chéo hình hộp
Công thức (Định lý Pythagore trong không gian):
$$d = \sqrt{a^2 + b^2 + h^2}$$
Trong đó:
- $d$: Độ dài đường chéo nối 2 đỉnh đối diện của hình hộp
- $a, b, h$: Ba kích thước của hình hộp
Chứng minh:
Trong tam giác vuông với:
- Cạnh 1: Đường chéo đáy = $\sqrt{a^2 + b^2}$
- Cạnh 2: Chiều cao = $h$
- Cạnh huyền: Đường chéo hình hộp = $d$
Áp dụng định lý Pythagore:
$$d^2 = (\sqrt{a^2 + b^2})^2 + h^2 = a^2 + b^2 + h^2$$
3. Ví dụ minh họa
Ví dụ 1: Hình hộp có $a = 6$cm, $b = 8$cm, $h = 10$cm. Tính đường chéo hình hộp.
Lời giải:
$$d = \sqrt{6^2 + 8^2 + 10^2} = \sqrt{36 + 64 + 100} = \sqrt{200} = 10\sqrt{2} \approx 14.14 \text{ cm}$$
Đáp án: $d = 10\sqrt{2}$ cm ≈ 14.14 cm
Ví dụ 2: Hình hộp có đường chéo 13cm, chiều dài 12cm, chiều rộng 4cm. Tính chiều cao.
Lời giải:
Từ công thức: $d^2 = a^2 + b^2 + h^2$
$$h^2 = d^2 – a^2 – b^2 = 13^2 – 12^2 – 4^2$$
$$h^2 = 169 – 144 – 16 = 9$$
$$h = 3 \text{ cm}$$
Đáp án: h = 3 cm
Ví dụ 3: Hình lập phương cạnh 5cm. Tính đường chéo.
Lời giải:
Với hình lập phương: $a = b = h = 5$ cm
$$d = \sqrt{5^2 + 5^2 + 5^2} = \sqrt{75} = 5\sqrt{3} \approx 8.66 \text{ cm}$$
Đáp án: $d = 5\sqrt{3}$ cm ≈ 8.66 cm
VII. Bảng Tổng Hợp Công Thức
Bảng 1: Công thức cơ bản
| Đại lượng | Công thức | Đơn vị |
|---|---|---|
| Diện tích đáy | $S_{\text{đáy}} = a \times b$ | cm², m² |
| Chu vi đáy | $P_{\text{đáy}} = 2(a + b)$ | cm, m |
| Diện tích xung quanh | $S_{xq} = 2(a + b) \times h$ | cm², m² |
| Diện tích toàn phần | $S_{tp} = S_{xq} + 2S_{\text{đáy}}$ | cm², m² |
| Diện tích toàn phần (trực tiếp) | $S_{tp} = 2(ab + ah + bh)$ | cm², m² |
| Thể tích | $V = a \times b \times h$ | cm³, m³, lít |
| Đường chéo | $d = \sqrt{a^2 + b^2 + h^2}$ | cm, m |
Bảng 2: Công thức tính chiều cao
| Cho trước | Công thức tính $h$ |
|---|---|
| Thể tích $V$, $a$, $b$ | $h = \frac{V}{ab}$ |
| Diện tích xung quanh $S_{xq}$, $a$, $b$ | $h = \frac{S_{xq}}{2(a+b)}$ |
| Đường chéo $d$, $a$, $b$ | $h = \sqrt{d^2 – a^2 – b^2}$ |
Bảng 3: Mối quan hệ công thức
S_tp = S_xq + 2S_đáy
S_xq = P_đáy × h = 2(a + b) × h
V = S_đáy × h = a × b × h
d² = a² + b² + h²
Bảng 4: Quy đổi đơn vị
Diện tích:
- 1 m² = 100 dm² = 10,000 cm²
- 1 dm² = 100 cm²
Thể tích:
- 1 m³ = 1,000 dm³ = 1,000 lít
- 1 dm³ = 1 lít = 1,000 cm³
- 1 cm³ = 1 ml
VIII. Các Dạng Bài Tập Thường Gặp
Dạng 1: Tính diện tích, thể tích khi biết 3 kích thước
Phương pháp: Áp dụng trực tiếp công thức
Bài 1: Hộp quà có kích thước 20cm × 15cm × 10cm. Tính diện tích giấy cần dán (diện tích toàn phần).
Lời giải:
$$S_{tp} = 2(20 \times 15 + 20 \times 10 + 15 \times 10)$$
$$S_{tp} = 2(300 + 200 + 150) = 2 \times 650 = 1,300 \text{ cm}^2$$
Đáp án: 1,300 cm²
Bài 2: Tủ lạnh dài 60cm, rộng 70cm, cao 180cm. Tính thể tích (lít).
Lời giải:
$$V = 60 \times 70 \times 180 = 756,000 \text{ cm}^3 = 756 \text{ lít}$$
Đáp án: 756 lít
Bài 3: Thùng carton 50cm × 40cm × 30cm. Tính diện tích xung quanh.
Lời giải:
$$S_{xq} = 2(50 + 40) \times 30 = 2 \times 90 \times 30 = 5,400 \text{ cm}^2$$
Đáp án: 5,400 cm²
Dạng 2: Tính chiều cao khi biết thể tích
Phương pháp: $h = \frac{V}{S_{\text{đáy}}} = \frac{V}{ab}$
Bài 4: Bể cá có thể tích 120 lít, đáy hình chữ nhật 60cm × 40cm. Tính chiều cao.
Lời giải:
- Đổi: 120 lít = 120 dm³
- Đổi đáy: 60cm × 40cm = 6dm × 4dm
- Chiều cao:
$$h = \frac{120}{6 \times 4} = \frac{120}{24} = 5 \text{ dm} = 50 \text{ cm}$$
Đáp án: h = 50 cm
Bài 5: Két nước có thể tích 500 lít, đáy 1m × 0.8m. Tính chiều cao.
Lời giải:
- Đổi: 500 lít = 0.5 m³
- Chiều cao:
$$h = \frac{0.5}{1 \times 0.8} = 0.625 \text{ m} = 62.5 \text{ cm}$$
Đáp án: h = 62.5 cm
Dạng 3: Tính chi phí sơn, dán
Phương pháp:
- Tính diện tích cần sơn (thường là $S_{xq}$ hoặc $S_{tp}$)
- Nhân với đơn giá
Bài 6: Phòng dài 6m, rộng 4m, cao 3m. Sơn trần và 4 tường (không sơn sàn). Sơn 1m² tốn 50,000đ. Tính chi phí.
Lời giải:
- Diện tích trần: $6 \times 4 = 24$ m²
- Diện tích 4 tường: $S_{xq} = 2(6 + 4) \times 3 = 60$ m²
- Tổng diện tích sơn: $24 + 60 = 84$ m²
- Chi phí: $84 \times 50,000 = 4,200,000$ đồng
Đáp án: 4,200,000 đồng
Bài 7: Bọc hộp quà 30cm × 25cm × 20cm. Giấy 8,000đ/m². Tính tiền (thêm 10% hao phí).
Lời giải:
- $S_{tp} = 2(30 \times 25 + 30 \times 20 + 25 \times 20)$
- $S_{tp} = 2(750 + 600 + 500) = 3,700$ cm² = 0.37 m²
- Diện tích thực tế: $0.37 \times 1.1 = 0.407$ m²
- Tiền: $0.407 \times 8,000 \approx 3,256$ đồng
Đáp án: ≈ 3,256 đồng
Dạng 4: Bài toán đổ nước vào bể
Phương pháp: $V_{\text{nước}} = a \times b \times h_{\text{nước}}$
Bài 8: Bể dài 2m, rộng 1.2m, cao 1.5m. Đổ nước đến 4/5 chiều cao. Tính lượng nước (lít).
Lời giải:
- Chiều cao nước: $h = 1.5 \times \frac{4}{5} = 1.2$ m
- Thể tích nước:
$$V = 2 \times 1.2 \times 1.2 = 2.88 \text{ m}^3 = 2,880 \text{ lít}$$
Đáp án: 2,880 lít
Bài 9: Bể 1.5m × 1m × 0.8m đang có 600 lít nước. Mực nước cao bao nhiêu?
Lời giải:
- Đổi: 600 lít = 0.6 m³
- Chiều cao nước:
$$h = \frac{0.6}{1.5 \times 1} = 0.4 \text{ m} = 40 \text{ cm}$$
Đáp án: 40 cm
Dạng 5: Tính kích thước khi biết thể tích và tỉ lệ
Phương pháp: Gọi kích thước theo ẩn, lập phương trình
Bài 10: Hình hộp có thể tích 240cm³, tỉ lệ chiều dài : rộng : cao = 4 : 3 : 2. Tính kích thước.
Lời giải:
- Gọi $a = 4x$, $b = 3x$, $h = 2x$
- Thể tích:
$$4x \times 3x \times 2x = 240$$
$$24x^3 = 240$$
$$x^3 = 10$$
$$x = \sqrt[3]{10} \approx 2.15$$
- Chiều dài: $a = 4\sqrt[3]{10} \approx 8.6$ cm
- Chiều rộng: $b = 3\sqrt[3]{10} \approx 6.5$ cm
- Chiều cao: $h = 2\sqrt[3]{10} \approx 4.3$ cm
Đáp án: $a \approx 8.6$ cm, $b \approx 6.5$ cm, $h \approx 4.3$ cm
Dạng 6: Tăng/giảm kích thước
Phương pháp: Tính thể tích mới, so sánh với thể tích cũ
Bài 11: Hộp có kích thước 10cm × 8cm × 5cm. Nếu tăng cả 3 kích thước lên 20%, thể tích tăng bao nhiêu %?
Lời giải:
- Thể tích cũ: $V_1 = 10 \times 8 \times 5 = 400$ cm³
- Kích thước mới: $12 \times 9.6 \times 6$ cm
- Thể tích mới: $V_2 = 12 \times 9.6 \times 6 = 691.2$ cm³
Cách 1:
$$\text{Tăng} = \frac{691.2 – 400}{400} \times 100% = 72.8%$$
Cách 2 (nhanh hơn):
$$(1.2)^3 = 1.728$$
Tăng: $72.8%$
Đáp án: Thể tích tăng 72.8%
IX. Bài Tập Thực Tế Vận Dụng
Bài 12: Tính dung tích tủ lạnh
Tủ lạnh có khoang chứa dài 50cm, rộng 40cm, cao 60cm. Tính dung tích (lít).
Lời giải:
$$V = 50 \times 40 \times 60 = 120,000 \text{ cm}^3 = 120 \text{ lít}$$
Đáp án: 120 lít
Bài 13: Tính diện tích hộp quà
Hộp quà kích thước 30cm × 20cm × 15cm. Cần bao nhiêu cm² giấy để bọc (không tính mép dán)?
Lời giải:
$$S_{tp} = 2(30 \times 20 + 30 \times 15 + 20 \times 15)$$
$$S_{tp} = 2(600 + 450 + 300) = 2,700 \text{ cm}^2$$
Đáp án: 2,700 cm²
Bài 14: Tính số gạch lát
Phòng dài 8m, rộng 6m. Dùng gạch 40cm × 40cm lát sàn. Cần bao nhiêu viên? (Hao phí 5%)
Lời giải:
- Diện tích sàn: $8 \times 6 = 48$ m² = 480,000 cm²
- Diện tích 1 viên gạch: $40 \times 40 = 1,600$ cm²
- Số viên cần: $\frac{480,000}{1,600} \times 1.05 = 315$ viên
Đáp án: 315 viên
Bài 15: Bể nước chứa bao lâu đầy
Bể dài 2.5m, rộng 1.2m, cao 1m. Vòi chảy 15 lít/phút. Bể đầy sau bao lâu?
Lời giải:
- Thể tích bể: $2.5 \times 1.2 \times 1 = 3$ m³ = 3,000 lít
- Thời gian: $\frac{3,000}{15} = 200$ phút = 3 giờ 20 phút
Đáp án: 3 giờ 20 phút
X. Kết Luận
Tổng kết công thức
Bài viết đã tổng hợp đầy đủ công thức về hình hộp chữ nhật:
Diện tích đáy: $S_{\text{đáy}} = ab$
Diện tích xung quanh: $S_{xq} = 2(a+b)h = P_{\text{đáy}} \times h$
Diện tích toàn phần: $S_{tp} = S_{xq} + 2S_{\text{đáy}} = 2(ab + ah + bh)$
Thể tích: $V = abh = S_{\text{đáy}} \times h$
Đường chéo: $d = \sqrt{a^2+b^2+h^2}$
Lưu ý quan trọng
Phân biệt rõ:
- Diện tích xung quanh (4 mặt bên)
- Diện tích toàn phần (6 mặt)
Chú ý đơn vị:
- Phải đổi về cùng đơn vị trước khi tính
- 1 dm³ = 1 lít (quan trọng cho bài toán nước)
- 1 m³ = 1,000 lít
Hình lập phương:
- Là trường hợp đặc biệt khi $a = b = h$
- Công thức: $V = a^3$, $S_{tp} = 6a^2$
Quy đổi:
- Diện tích: 1 m² = 10,000 cm²
- Thể tích: 1 m³ = 1,000,000 cm³

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
