Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ HÌNH TRỤ
- 1. Hình trụ là gì?
- 2. Các loại hình trụ
- 3. Phân biệt hình trụ và khối trụ
- 5. Cấu trúc bài viết
- II. CÁC THÀNH PHẦN CƠ BẢN CỦA HÌNH TRỤ
- 1. Sơ đồ minh họa các thành phần
- 2. Các đại lượng cần biết
- 3. Mối quan hệ giữa các đại lượng
- 4. Lưu ý về đơn vị
- III. CÔNG THỨC DIỆN TÍCH ĐÁY HÌNH TRỤ
- 1. Công thức tính diện tích đáy
- 2. Ví dụ minh họa
- 3. Lưu ý quan trọng
- IV. CÔNG THỨC DIỆN TÍCH XUNG QUANH HÌNH TRỤ
- 1. Khái niệm diện tích xung quanh
- 2. Cách suy ra công thức
- 3. Công thức diện tích xung quanh
- 4. Ví dụ minh họa
- V. CÔNG THỨC DIỆN TÍCH TOÀN PHẦN HÌNH TRỤ
- 1. Khái niệm diện tích toàn phần
- 2. Công thức diện tích toàn phần
- 3. Cách nhớ công thức
- 4. Ví dụ minh họa
- 5. Ứng dụng thực tế
- VI. CÔNG THỨC THỂ TÍCH HÌNH TRỤ
- 1. Khái niệm thể tích
- 2. Cách suy ra công thức
- 3. Công thức thể tích hình trụ
- 4. Quy đổi đơn vị thể tích
- 5. Ví dụ minh họa
- VII. CÔNG THỨC TÍNH NGƯỢC CÁC ĐẠI LƯỢNG
- 1. Công thức tính bán kính đáy (r)
- 2. Công thức tính chiều cao (h)
- 3. Công thức tính đường kính (d)
- 4. Bảng tổng hợp công thức tính ngược
- VIII. BẢNG TỔNG HỢP TẤT CẢ CÔNG THỨC HÌNH TRỤ
- Bảng công thức chính
- Công thức quan hệ
- IX. BÀI TẬP MẪU CÓ LỜI GIẢI CHI TIẾT
- Dạng 1: Tính diện tích và thể tích khi biết r và h
- Dạng 2: Tính khi biết đường kính
- Dạng 3: Tính ngược chiều cao khi biết thể tích
- Dạng 4: Tính bán kính khi biết diện tích xung quanh
- Dạng 5: Bài toán thực tế – Bể chứa nước
- Dạng 6: So sánh thể tích
- Dạng 7: Tính chi phí vật liệu
- X. MẸO VÀ LƯU Ý KHI TÍNH TOÁN
- 1. Các sai lầm thường gặp
- 2. Mẹo nhớ công thức
- 3. Các bước giải bài tập hình trụ
- 4. Kiểm tra kết quả
- 5. Giá trị π cần nhớ
- 6. Quy đổi đơn vị nhanh
- 7. Lưu ý đặc biệt
- XI. KẾT LUẬN
- Tài liệu tham khảo và học thêm
I. GIỚI THIỆU VỀ HÌNH TRỤ
1. Hình trụ là gì?
Định nghĩa hình trụ: Hình trụ là khối hình học không gian được tạo thành khi quay một hình chữ nhật quanh một cạnh cố định của nó.
Định nghĩa hình trụ tròn xoay: Hình trụ tròn xoay là trường hợp đặc biệt và phổ biến nhất của hình trụ, trong đó đường sinh vuông góc với hai đáy và hai đáy là hai hình tròn bằng nhau, song song với nhau.
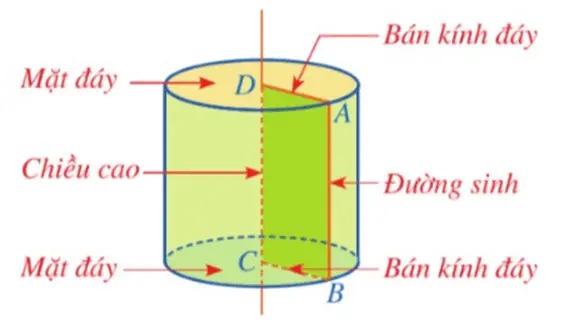
Các yếu tố cấu tạo nên hình trụ:
- Hai đáy: Là hai hình tròn bằng nhau, nằm trên hai mặt phẳng song song
- Mặt xung quanh: Là mặt cong nối hai đường tròn đáy
- Trục: Là đường thẳng nối tâm hai đường tròn đáy
- Chiều cao (h): Là khoảng cách giữa hai mặt phẳng chứa hai đáy
- Bán kính đáy (r): Là bán kính của hình tròn đáy
- Đường sinh (l): Là đoạn thẳng nối hai điểm tương ứng trên hai đường tròn đáy, song song với trục
2. Các loại hình trụ
Hình trụ tròn xoay (hình trụ đứng):
- Đường sinh vuông góc với đáy
- Đường sinh song song với trục
- Trong hình trụ tròn xoay: $l = h$ (đường sinh bằng chiều cao)
- Đây là loại hình trụ phổ biến nhất và là trọng tâm của bài viết
Hình trụ xiên:
- Đường sinh không vuông góc với đáy
- Đường sinh tạo góc với trục
- Ít gặp trong chương trình phổ thông
Lưu ý: Trong bài viết này, chúng ta tập trung vào hình trụ tròn xoay – loại hình trụ xuất hiện trong chương trình toán phổ thông và hầu hết các ứng dụng thực tế.
3. Phân biệt hình trụ và khối trụ
Hình trụ:
- Là bề mặt bao gồm hai đáy và mặt xung quanh
- Chỉ tính đến “vỏ ngoài” của khối
- Khi nói “diện tích hình trụ” là diện tích bề mặt
Khối trụ:
- Là phần không gian bên trong hình trụ
- Bao gồm cả phần rắn bên trong
- Khi nói “thể tích khối trụ” là không gian bên trong
Trong thực tế:
- Thể tích của hình trụ = Thể tích của khối trụ
- Hai thuật ngữ thường được dùng thay thế cho nhau
- Đề bài thường dùng “hình trụ” cho cả hai trường hợp
5. Cấu trúc bài viết
Bài viết được tổ chức theo hệ thống từ cơ bản đến nâng cao:
- Phần II: Các thành phần cơ bản của hình trụ và ký hiệu
- Phần III: Công thức diện tích đáy hình trụ
- Phần IV: Công thức diện tích xung quanh hình trụ
- Phần V: Công thức diện tích toàn phần hình trụ
- Phần VI: Công thức thể tích hình trụ
- Phần VII: Công thức tính ngược các đại lượng (r, h, d)
- Phần VIII: Bảng tổng hợp tất cả công thức
- Phần IX: 7 dạng bài tập mẫu có lời giải chi tiết
- Phần X: Mẹo nhớ và lưu ý khi tính toán
II. CÁC THÀNH PHẦN CƠ BẢN CỦA HÌNH TRỤ
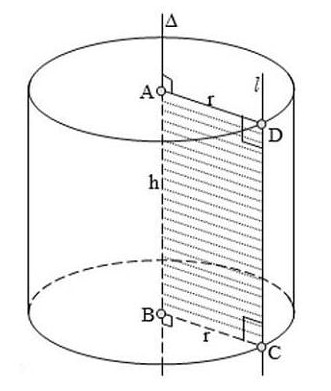
1. Sơ đồ minh họa các thành phần
Giải thích hình vẽ:
- Hai đường tròn trên và dưới là hai đáy của hình trụ
- Đường thẳng nối tâm C của hai đáy là trục (cũng là chiều cao h)
- Khoảng cách từ tâm đến mép đường tròn là bán kính r
- Mặt cong bao quanh là mặt xung quanh
2. Các đại lượng cần biết
| Ký hiệu | Tên gọi | Đơn vị thường dùng | Ghi chú |
|---|---|---|---|
| $r$ | Bán kính đáy | cm, m, dm | Bán kính hình tròn đáy |
| $d$ | Đường kính đáy | cm, m, dm | $d = 2r$ |
| $h$ | Chiều cao | cm, m, dm | Khoảng cách giữa hai đáy |
| $l$ | Đường sinh | cm, m, dm | Với hình trụ tròn: $l = h$ |
| $S_{đáy}$ | Diện tích đáy | cm², m², dm² | Diện tích hình tròn |
| $S_{xq}$ | Diện tích xung quanh | cm², m², dm² | Diện tích mặt cong |
| $S_{tp}$ | Diện tích toàn phần | cm², m², dm² | Tổng diện tích bề mặt |
| $V$ | Thể tích | cm³, m³, dm³, lít | Không gian bên trong |
| $C$ | Chu vi đáy | cm, m, dm | Chu vi hình tròn đáy |
3. Mối quan hệ giữa các đại lượng
Mối quan hệ cơ bản:
- Với hình trụ tròn xoay: Đường sinh = Chiều cao, tức là $l = h$
- Đường kính gấp đôi bán kính: $d = 2r$, hay $r = \frac{d}{2}$
- Chu vi đáy: $C = 2\pi r = \pi d$
- Diện tích đáy: $S_{đáy} = \pi r^2 = \frac{\pi d^2}{4}$
Lưu ý quan trọng:
- Hai đáy của hình trụ luôn bằng nhau
- Trong hình trụ tròn xoay, trục luôn vuông góc với đáy
- Mọi đường sinh của hình trụ tròn đều song song với nhau và bằng nhau
4. Lưu ý về đơn vị
Đơn vị độ dài:
- Thường dùng: cm (centimét), m (mét), dm (decimét)
- Quy đổi: 1 m = 100 cm = 10 dm
Đơn vị diện tích:
- Luôn là đơn vị bình phương: cm², m², dm²
- Quy đổi: 1 m² = 10000 cm² = 100 dm²
Đơn vị thể tích:
- Luôn là đơn vị khối: cm³, m³, dm³
- Đơn vị đặc biệt: lít (l hoặc L)
Quy đổi thể tích quan trọng:
- 1 lít = 1 dm³ = 1000 cm³
- 1 m³ = 1000 lít = 1000 dm³ = 1000000 cm³
- 1 mililít (ml) = 1 cm³
Nguyên tắc khi tính toán:
- Đổi tất cả các đại lượng về cùng một hệ đơn vị trước khi tính
- Kết quả diện tích phải có đơn vị bình phương
- Kết quả thể tích phải có đơn vị khối
III. CÔNG THỨC DIỆN TÍCH ĐÁY HÌNH TRỤ
1. Công thức tính diện tích đáy
Vì đáy của hình trụ là hình tròn, nên diện tích đáy được tính theo công thức diện tích hình tròn:
$$\boxed{S_{đáy} = \pi r^2}$$
Hoặc nếu biết đường kính $d = 2r$:
$$\boxed{S_{đáy} = \pi \left(\frac{d}{2}\right)^2 = \frac{\pi d^2}{4}}$$
Trong đó:
- $S_{đáy}$: Diện tích một đáy (đơn vị: cm², m², dm²)
- $r$: Bán kính đáy (đơn vị: cm, m, dm)
- $d$: Đường kính đáy (đơn vị: cm, m, dm)
- $\pi \approx 3.14$ hoặc $\pi = \frac{22}{7}$ (số pi)
2. Ví dụ minh họa
Ví dụ 1: Tính diện tích đáy hình trụ có bán kính $r = 5$ cm.
Lời giải: $$S_{đáy} = \pi r^2 = 3.14 \times 5^2 = 3.14 \times 25 = 78.5 \text{ cm}^2$$
Đáp số: $S_{đáy} = 78.5$ cm²
Ví dụ 2: Tính diện tích đáy hình trụ có đường kính $d = 12$ cm.
Lời giải:
Cách 1: Tính bán kính rồi áp dụng công thức
- Bán kính: $r = \frac{d}{2} = \frac{12}{2} = 6$ cm
- Diện tích đáy: $S_{đáy} = \pi r^2 = 3.14 \times 6^2 = 3.14 \times 36 = 113.04$ cm²
Cách 2: Dùng công thức với đường kính $$S_{đáy} = \frac{\pi d^2}{4} = \frac{3.14 \times 12^2}{4} = \frac{3.14 \times 144}{4} = \frac{452.16}{4} = 113.04 \text{ cm}^2$$
Đáp số: $S_{đáy} = 113.04$ cm²
3. Lưu ý quan trọng
Về số lượng đáy:
- Công thức $S_{đáy} = \pi r^2$ tính diện tích một đáy
- Hình trụ có hai đáy giống hệt nhau
- Tổng diện tích hai đáy: $2S_{đáy} = 2\pi r^2$
Về đơn vị:
- Đơn vị diện tích luôn là bình phương của đơn vị độ dài
- Nếu $r$ tính bằng cm thì $S_{đáy}$ tính bằng cm²
- Nếu $r$ tính bằng m thì $S_{đáy}$ tính bằng m²
Mẹo nhớ:
“Diện tích đáy = Pi nhân bán kính bình phương”
IV. CÔNG THỨC DIỆN TÍCH XUNG QUANH HÌNH TRỤ
1. Khái niệm diện tích xung quanh
Định nghĩa: Diện tích xung quanh là diện tích của mặt cong bao quanh hình trụ, không bao gồm hai đáy.
Ý nghĩa thực tế:
- Diện tích nhãn dán quanh lon nước ngọt
- Diện tích vải bọc xung quanh ống
- Diện tích sơn mặt bên cột trụ (không sơn đáy)
2. Cách suy ra công thức
Phương pháp trải phẳng:
Nếu cắt dọc và trải phẳng mặt xung quanh của hình trụ ra, ta được một hình chữ nhật với:
- Chiều dài: Bằng chu vi đáy = $2\pi r$
- Chiều rộng: Bằng chiều cao hình trụ = $h$
Diện tích hình chữ nhật: $$S_{xq} = \text{Chiều dài} \times \text{Chiều rộng} = 2\pi r \times h$$
3. Công thức diện tích xung quanh
$$\boxed{S_{xq} = 2\pi rh}$$
Hoặc nếu biết đường kính $d = 2r$:
$$\boxed{S_{xq} = \pi dh}$$
Trong đó:
- $S_{xq}$: Diện tích xung quanh (đơn vị: cm², m², dm²)
- $r$: Bán kính đáy (đơn vị: cm, m, dm)
- $h$: Chiều cao (đơn vị: cm, m, dm)
- $d$: Đường kính đáy (đơn vị: cm, m, dm)
- $\pi \approx 3.14$
4. Ví dụ minh họa
Ví dụ 1: Tính diện tích xung quanh hình trụ có bán kính đáy $r = 4$ cm và chiều cao $h = 10$ cm.
Lời giải: $$S_{xq} = 2\pi rh = 2 \times 3.14 \times 4 \times 10 = 251.2 \text{ cm}^2$$
Đáp số: $S_{xq} = 251.2$ cm²
Ví dụ 2: Một lon nước ngọt hình trụ có đường kính đáy 6 cm, chiều cao 12 cm. Tính diện tích nhãn dán bọc quanh lon (diện tích xung quanh).
Lời giải:
Bước 1: Tính bán kính
- $r = \frac{d}{2} = \frac{6}{2} = 3$ cm
Bước 2: Tính diện tích xung quanh $$S_{xq} = 2\pi rh = 2 \times 3.14 \times 3 \times 12 = 226.08 \text{ cm}^2$$
Đáp số: Diện tích nhãn dán cần 226.08 cm²
Ví dụ 3: Tính diện tích xung quanh hình trụ khi biết đường kính $d = 8$ cm và chiều cao $h = 15$ cm.
Lời giải:
Dùng công thức với đường kính: $$S_{xq} = \pi dh = 3.14 \times 8 \times 15 = 376.8 \text{ cm}^2$$
Đáp số: $S_{xq} = 376.8$ cm²
Mẹo nhớ:
“Diện tích xung quanh = Chu vi đáy nhân chiều cao” $S_{xq} = 2\pi r \times h$
V. CÔNG THỨC DIỆN TÍCH TOÀN PHẦN HÌNH TRỤ
1. Khái niệm diện tích toàn phần
Định nghĩa: Diện tích toàn phần là tổng diện tích tất cả các mặt của hình trụ, bao gồm:
- Mặt đáy trên
- Mặt đáy dưới
- Mặt xung quanh (mặt cong)
Ý nghĩa thực tế:
- Diện tích vật liệu cần để làm một lon kín (có nắp)
- Diện tích cần sơn toàn bộ bề mặt cột trụ
- Diện tích tôn cần để làm thùng phuy kín
2. Công thức diện tích toàn phần
Công thức tổng quát: $$S_{tp} = S_{xq} + 2S_{đáy}$$
Khai triển: $$S_{tp} = 2\pi rh + 2\pi r^2$$
Rút gọn: $$\boxed{S_{tp} = 2\pi r(h + r)}$$
Hoặc nếu biết đường kính: $$S_{tp} = \pi dh + \frac{\pi d^2}{2}$$
Trong đó:
- $S_{tp}$: Diện tích toàn phần (đơn vị: cm², m², dm²)
- $S_{xq}$: Diện tích xung quanh
- $S_{đáy}$: Diện tích một đáy
- $r$: Bán kính đáy (đơn vị: cm, m, dm)
- $h$: Chiều cao (đơn vị: cm, m, dm)
- $d$: Đường kính đáy
3. Cách nhớ công thức
Cách 1: Nhớ theo thành phần $$S_{tp} = \underbrace{2\pi rh}{S{xq}} + \underbrace{2\pi r^2}{2S{đáy}}$$
“Toàn phần = Xung quanh + Hai đáy”
Cách 2: Nhớ dạng rút gọn $$S_{tp} = 2\pi r(h + r)$$
“2 pi r nhân với (chiều cao cộng bán kính)”
4. Ví dụ minh họa
Ví dụ 1: Tính diện tích toàn phần hình trụ có $r = 5$ cm và $h = 12$ cm.
Lời giải:
Cách 1: Tính từng phần rồi cộng lại
- Diện tích một đáy: $S_{đáy} = \pi r^2 = 3.14 \times 5^2 = 78.5$ cm²
- Diện tích hai đáy: $2S_{đáy} = 2 \times 78.5 = 157$ cm²
- Diện tích xung quanh: $S_{xq} = 2\pi rh = 2 \times 3.14 \times 5 \times 12 = 376.8$ cm²
- Diện tích toàn phần: $S_{tp} = 157 + 376.8 = 533.8$ cm²
Cách 2: Dùng công thức rút gọn (nhanh hơn) $$S_{tp} = 2\pi r(h + r) = 2 \times 3.14 \times 5 \times (12 + 5)$$ $$= 2 \times 3.14 \times 5 \times 17 = 31.4 \times 17 = 533.8 \text{ cm}^2$$
Đáp số: $S_{tp} = 533.8$ cm²
Ví dụ 2: Một bể nước hình trụ có đường kính 2m, chiều cao 1.5m. Tính diện tích cần ốp gạch để lát toàn bộ bề mặt trong của bể (kể cả đáy).
Lời giải:
Bước 1: Xác định các đại lượng
- Đường kính: $d = 2$ m
- Bán kính: $r = \frac{d}{2} = 1$ m
- Chiều cao: $h = 1.5$ m
Bước 2: Tính diện tích toàn phần $$S_{tp} = 2\pi r(h + r) = 2 \times 3.14 \times 1 \times (1.5 + 1)$$ $$= 6.28 \times 2.5 = 15.7 \text{ m}^2$$
Đáp số: Cần ốp 15.7 m² gạch.
Ví dụ 3: Làm một thùng sơn hình trụ bằng tôn (kín cả hai đầu), có bán kính đáy 20cm và chiều cao 40cm. Tính diện tích tôn cần dùng.
Lời giải:
Bước 1: Đổi đơn vị về cùng hệ
- $r = 20$ cm
- $h = 40$ cm
Bước 2: Tính diện tích toàn phần $$S_{tp} = 2\pi r(h + r) = 2 \times 3.14 \times 20 \times (40 + 20)$$ $$= 2 \times 3.14 \times 20 \times 60 = 7536 \text{ cm}^2$$
Đổi sang m²: $S_{tp} = \frac{7536}{10000} = 0.7536$ m²
Đáp số: Cần 7536 cm² = 0.7536 m² tôn.
5. Ứng dụng thực tế
Tính lượng vật liệu:
- Làm bể chứa kín
- Làm lon, hộp kim loại
- Làm thùng phuy kín
Tính chi phí:
- Chi phí sơn toàn bộ bề mặt
- Chi phí ốp gạch bể nước
- Chi phí làm vỏ lon
Lưu ý:
- Nếu đề bài nói “không có nắp” hoặc “hở đáy” → chỉ tính $S_{xq} + S_{đáy}$
- Nếu đề bài nói “kín”, “có nắp”, “toàn bộ bề mặt” → tính $S_{tp}$
VI. CÔNG THỨC THỂ TÍCH HÌNH TRỤ
1. Khái niệm thể tích
Định nghĩa: Thể tích hình trụ là không gian bên trong hình trụ, tức là lượng chất lỏng hoặc chất rắn mà hình trụ có thể chứa được.
Ý nghĩa thực tế:
- Dung tích nước trong bình, bể, thùng
- Lượng nước trong lon, chai
- Thể tích bê tông cần để đổ cột trụ
- Dung tích xi lanh động cơ
2. Cách suy ra công thức
Nguyên lý: Thể tích của một khối lăng trụ (kể cả hình trụ) bằng diện tích đáy nhân với chiều cao.
$$\text{Thể tích} = \text{Diện tích đáy} \times \text{Chiều cao}$$
$$V = S_{đáy} \times h = \pi r^2 \times h$$
3. Công thức thể tích hình trụ
$$\boxed{V = \pi r^2 h}$$
Hoặc nếu biết đường kính $d = 2r$:
$$\boxed{V = \pi \left(\frac{d}{2}\right)^2 h = \frac{\pi d^2 h}{4}}$$
Trong đó:
- $V$: Thể tích (đơn vị: cm³, m³, dm³, lít)
- $r$: Bán kính đáy (đơn vị: cm, m, dm)
- $h$: Chiều cao (đơn vị: cm, m, dm)
- $d$: Đường kính đáy (đơn vị: cm, m, dm)
- $\pi \approx 3.14$ hoặc $\pi = \frac{22}{7}$
4. Quy đổi đơn vị thể tích
Bảng quy đổi thể tích:
| Đơn vị gốc | Quy đổi |
|---|---|
| 1 lít (l) | = 1 dm³ = 1000 cm³ |
| 1 m³ | = 1000 lít = 1000 dm³ = 1000000 cm³ |
| 1 dm³ | = 1000 cm³ = 1 lít |
| 1 cm³ | = 1 ml (mililít) |
| 1 kilolít (kl) | = 1 m³ = 1000 lít |
Lưu ý:
- 1 lít nước = 1 dm³ = 1 kg (ở điều kiện tiêu chuẩn)
- Lon nước ngọt thường 330ml = 330 cm³
5. Ví dụ minh họa
Ví dụ 1: Tính thể tích hình trụ có bán kính đáy $r = 7$ cm và chiều cao $h = 10$ cm.
Lời giải: $$V = \pi r^2 h = 3.14 \times 7^2 \times 10$$ $$= 3.14 \times 49 \times 10$$ $$= 1538.6 \text{ cm}^3$$
Đáp số: $V = 1538.6$ cm³
Ví dụ 2: Một bình nước hình trụ có đường kính đáy 20 cm, chiều cao 30 cm. Tính thể tích nước bình chứa được. Đổi kết quả ra lít.
Lời giải:
Bước 1: Tính bán kính
- $r = \frac{d}{2} = \frac{20}{2} = 10$ cm
Bước 2: Tính thể tích $$V = \pi r^2 h = 3.14 \times 10^2 \times 30$$ $$= 3.14 \times 100 \times 30 = 9420 \text{ cm}^3$$
Bước 3: Đổi sang lít $$V = \frac{9420}{1000} = 9.42 \text{ lít}$$
Đáp số: Bình chứa được 9.42 lít nước.
Ví dụ 3: Tính thể tích hình trụ khi biết đường kính $d = 14$ cm và chiều cao $h = 20$ cm.
Lời giải:
Dùng công thức với đường kính: $$V = \frac{\pi d^2 h}{4} = \frac{3.14 \times 14^2 \times 20}{4}$$ $$= \frac{3.14 \times 196 \times 20}{4} = \frac{12307.2}{4} = 3076.8 \text{ cm}^3$$
Đáp số: $V = 3076.8$ cm³
Ví dụ 4: Một ống nước hình trụ dài 5m, đường kính trong 10cm. Tính thể tích nước trong ống khi đầy.
Lời giải:
Bước 1: Đổi đơn vị về cùng hệ
- Chiều dài (chiều cao): $h = 5$ m $= 500$ cm
- Đường kính: $d = 10$ cm
- Bán kính: $r = 5$ cm
Bước 2: Tính thể tích $$V = \pi r^2 h = 3.14 \times 5^2 \times 500$$ $$= 3.14 \times 25 \times 500 = 39250 \text{ cm}^3$$
Bước 3: Đổi sang lít $$V = \frac{39250}{1000} = 39.25 \text{ lít}$$
Đáp số: Ống chứa 39.25 lít nước.
Mẹo nhớ:
“Thể tích = Pi nhân bán kính bình phương nhân chiều cao” $V = \pi r^2 h$
VII. CÔNG THỨC TÍNH NGƯỢC CÁC ĐẠI LƯỢNG
Trong nhiều bài toán thực tế, ta biết một số đại lượng và cần tính các đại lượng còn lại.
1. Công thức tính bán kính đáy (r)
A. Khi biết diện tích đáy ($S_{đáy}$):
Từ công thức: $S_{đáy} = \pi r^2$
$$\boxed{r = \sqrt{\frac{S_{đáy}}{\pi}}}$$
Ví dụ: Hình trụ có diện tích đáy 78.5 cm². Tính bán kính.
Lời giải: $$r = \sqrt{\frac{78.5}{3.14}} = \sqrt{25} = 5 \text{ cm}$$
B. Khi biết thể tích (V) và chiều cao (h):
Từ công thức: $V = \pi r^2 h$
$$\boxed{r = \sqrt{\frac{V}{\pi h}}}$$
Ví dụ: Hình trụ có thể tích 1570 cm³ và chiều cao 10 cm. Tính bán kính.
Lời giải: $$r = \sqrt{\frac{1570}{3.14 \times 10}} = \sqrt{\frac{1570}{31.4}} = \sqrt{50} \approx 7.07 \text{ cm}$$
C. Khi biết diện tích xung quanh ($S_{xq}$) và chiều cao (h):
Từ công thức: $S_{xq} = 2\pi rh$
$$\boxed{r = \frac{S_{xq}}{2\pi h}}$$
Ví dụ: Hình trụ có $S_{xq} = 314$ cm² và chiều cao 10 cm. Tính bán kính.
Lời giải: $$r = \frac{314}{2 \times 3.14 \times 10} = \frac{314}{62.8} = 5 \text{ cm}$$
D. Khi biết đường kính (d):
$$\boxed{r = \frac{d}{2}}$$
Ví dụ: Hình trụ có đường kính 16 cm. Tính bán kính.
Lời giải: $$r = \frac{16}{2} = 8 \text{ cm}$$
2. Công thức tính chiều cao (h)
A. Khi biết thể tích (V) và bán kính (r):
Từ công thức: $V = \pi r^2 h$
$$\boxed{h = \frac{V}{\pi r^2}}$$
Ví dụ: Hình trụ có thể tích 1570 cm³ và bán kính 5 cm. Tính chiều cao.
Lời giải: $$h = \frac{1570}{3.14 \times 5^2} = \frac{1570}{3.14 \times 25} = \frac{1570}{78.5} = 20 \text{ cm}$$
B. Khi biết diện tích xung quanh ($S_{xq}$) và bán kính (r):
Từ công thức: $S_{xq} = 2\pi rh$
$$\boxed{h = \frac{S_{xq}}{2\pi r}}$$
Ví dụ: Hình trụ có $S_{xq} = 314$ cm² và bán kính 5 cm. Tính chiều cao.
Lời giải: $$h = \frac{314}{2 \times 3.14 \times 5} = \frac{314}{31.4} = 10 \text{ cm}$$
C. Khi biết diện tích toàn phần ($S_{tp}$) và bán kính (r):
Từ công thức: $S_{tp} = 2\pi r(h + r)$
$$\boxed{h = \frac{S_{tp}}{2\pi r} – r}$$
Ví dụ: Hình trụ có $S_{tp} = 471$ cm² và bán kính 5 cm. Tính chiều cao.
Lời giải: $$h = \frac{471}{2 \times 3.14 \times 5} – 5 = \frac{471}{31.4} – 5 = 15 – 5 = 10 \text{ cm}$$
3. Công thức tính đường kính (d)
$$\boxed{d = 2r}$$
Hoặc từ các công thức tính $r$ ở trên, ta nhân đôi kết quả để được $d$.
Ví dụ: Hình trụ có bán kính 8 cm. Tính đường kính.
Lời giải: $$d = 2r = 2 \times 8 = 16 \text{ cm}$$
4. Bảng tổng hợp công thức tính ngược
| Cần tính | Biết | Công thức |
|---|---|---|
| $r$ | $S_{đáy}$ | $r = \sqrt{\frac{S_{đáy}}{\pi}}$ |
| $r$ | $V, h$ | $r = \sqrt{\frac{V}{\pi h}}$ |
| $r$ | $S_{xq}, h$ | $r = \frac{S_{xq}}{2\pi h}$ |
| $r$ | $d$ | $r = \frac{d}{2}$ |
| $h$ | $V, r$ | $h = \frac{V}{\pi r^2}$ |
| $h$ | $S_{xq}, r$ | $h = \frac{S_{xq}}{2\pi r}$ |
| $h$ | $S_{tp}, r$ | $h = \frac{S_{tp}}{2\pi r} – r$ |
| $d$ | $r$ | $d = 2r$ |
| $S_{đáy}$ | $r$ | $S_{đáy} = \pi r^2$ |
| $S_{xq}$ | $r, h$ | $S_{xq} = 2\pi rh$ |
| $V$ | $r, h$ | $V = \pi r^2 h$ |
VIII. BẢNG TỔNG HỢP TẤT CẢ CÔNG THỨC HÌNH TRỤ
Bảng công thức chính
| Đại lượng | Công thức (theo r) | Công thức (theo d) | Đơn vị |
|---|---|---|---|
| Diện tích đáy | $S_{đáy} = \pi r^2$ | $S_{đáy} = \frac{\pi d^2}{4}$ | cm², m², dm² |
| Diện tích xung quanh | $S_{xq} = 2\pi rh$ | $S_{xq} = \pi dh$ | cm², m², dm² |
| Diện tích toàn phần | $S_{tp} = 2\pi r(h + r)$ | $S_{tp} = \pi dh + \frac{\pi d^2}{2}$ | cm², m², dm² |
| Thể tích | $V = \pi r^2 h$ | $V = \frac{\pi d^2 h}{4}$ | cm³, m³, dm³, lít |
| Chu vi đáy | $C = 2\pi r$ | $C = \pi d$ | cm, m, dm |
| Bán kính | – | $r = \frac{d}{2}$ | cm, m, dm |
| Đường kính | $d = 2r$ | – | cm, m, dm |
Công thức quan hệ
| Công thức | Ý nghĩa |
|---|---|
| $d = 2r$ hoặc $r = \frac{d}{2}$ | Đường kính và bán kính |
| $l = h$ | Đường sinh = Chiều cao (hình trụ tròn) |
| $S_{tp} = S_{xq} + 2S_{đáy}$ | Toàn phần = Xung quanh + Hai đáy |
| $V = S_{đáy} \times h$ | Thể tích = Diện tích đáy × Chiều cao |
IX. BÀI TẬP MẪU CÓ LỜI GIẢI CHI TIẾT
Dạng 1: Tính diện tích và thể tích khi biết r và h
Bài 1: Cho hình trụ có bán kính đáy $r = 6$ cm và chiều cao $h = 15$ cm. Tính: a) Diện tích xung quanh
b) Diện tích toàn phần
c) Thể tích
Lời giải:
Câu a) Diện tích xung quanh: $$S_{xq} = 2\pi rh = 2 \times 3.14 \times 6 \times 15$$ $$= 6.28 \times 6 \times 15 = 565.2 \text{ cm}^2$$
Câu b) Diện tích toàn phần:
Cách 1 (tính từng phần):
- Diện tích đáy: $S_{đáy} = \pi r^2 = 3.14 \times 36 = 113.04$ cm²
- Diện tích hai đáy: $2S_{đáy} = 226.08$ cm²
- Diện tích toàn phần: $S_{tp} = 565.2 + 226.08 = 791.28$ cm²
Cách 2 (công thức rút gọn – nhanh hơn): $$S_{tp} = 2\pi r(h + r) = 2 \times 3.14 \times 6 \times (15 + 6)$$ $$= 6.28 \times 6 \times 21 = 791.28 \text{ cm}^2$$
Câu c) Thể tích: $$V = \pi r^2 h = 3.14 \times 6^2 \times 15$$ $$= 3.14 \times 36 \times 15 = 1695.6 \text{ cm}^3$$
Đáp số:
- a) $S_{xq} = 565.2$ cm²
- b) $S_{tp} = 791.28$ cm²
- c) $V = 1695.6$ cm³
Dạng 2: Tính khi biết đường kính
Bài 2: Một lon sữa hình trụ có đường kính đáy 8 cm, chiều cao 12 cm. Tính: a) Diện tích nhãn dán bọc quanh lon (diện tích xung quanh)
b) Dung tích lon (thể tích) tính bằng lít
Lời giải:
Xác định đại lượng:
- Đường kính: $d = 8$ cm
- Bán kính: $r = \frac{d}{2} = \frac{8}{2} = 4$ cm
- Chiều cao: $h = 12$ cm
Câu a) Diện tích nhãn dán: $$S_{xq} = 2\pi rh = 2 \times 3.14 \times 4 \times 12$$ $$= 6.28 \times 48 = 301.44 \text{ cm}^2$$
Câu b) Dung tích: $$V = \pi r^2 h = 3.14 \times 4^2 \times 12$$ $$= 3.14 \times 16 \times 12 = 602.88 \text{ cm}^3$$
Đổi sang lít: $$V = \frac{602.88}{1000} = 0.603 \text{ lít} \approx 603 \text{ ml}$$
Đáp số:
- a) Diện tích nhãn: 301.44 cm²
- b) Dung tích: 0.603 lít (603 ml)
Dạng 3: Tính ngược chiều cao khi biết thể tích
Bài 3: Một bể nước hình trụ có thể tích 3.14 m³ và bán kính đáy 1 m. Tính chiều cao của bể.
Lời giải:
Từ công thức thể tích: $V = \pi r^2 h$
Suy ra chiều cao: $$h = \frac{V}{\pi r^2} = \frac{3.14}{3.14 \times 1^2} = \frac{3.14}{3.14} = 1 \text{ m}$$
Đáp số: Chiều cao bể là 1 m.
Dạng 4: Tính bán kính khi biết diện tích xung quanh
Bài 4: Hình trụ có diện tích xung quanh 628 cm² và chiều cao 20 cm. Tính bán kính đáy.
Lời giải:
Từ công thức: $S_{xq} = 2\pi rh$
Suy ra bán kính: $$r = \frac{S_{xq}}{2\pi h} = \frac{628}{2 \times 3.14 \times 20}$$ $$= \frac{628}{125.6} = 5 \text{ cm}$$
Đáp số: Bán kính đáy là 5 cm.
Dạng 5: Bài toán thực tế – Bể chứa nước
Bài 5: Một bể nước hình trụ có đường kính 2m và chiều sâu 1.5m. a) Tính thể tích nước bể chứa được khi đầy (tính cả m³ và lít)
b) Nếu mỗi ngày dùng 500 lít nước, hỏi đầy bể dùng được khoảng bao nhiêu ngày?
Lời giải:
Xác định đại lượng:
- Đường kính: $d = 2$ m
- Bán kính: $r = \frac{d}{2} = 1$ m
- Chiều cao (độ sâu): $h = 1.5$ m
Câu a) Thể tích nước: $$V = \pi r^2 h = 3.14 \times 1^2 \times 1.5$$ $$= 3.14 \times 1.5 = 4.71 \text{ m}^3$$
Đổi sang lít: $$V = 4.71 \times 1000 = 4710 \text{ lít}$$
Câu b) Số ngày dùng được: $$\text{Số ngày} = \frac{4710}{500} = 9.42 \text{ ngày}$$
Làm tròn: Đầy bể dùng được khoảng 9 ngày.
Đáp số:
- a) Thể tích: 4.71 m³ = 4710 lít
- b) Dùng được khoảng 9 ngày
Dạng 6: So sánh thể tích
Bài 6: Hình trụ A có $r_A = 4$ cm, $h_A = 10$ cm. Hình trụ B có $r_B = 5$ cm, $h_B = 8$ cm. Hình nào có thể tích lớn hơn?
Lời giải:
Thể tích hình trụ A: $$V_A = \pi r_A^2 h_A = 3.14 \times 4^2 \times 10$$ $$= 3.14 \times 16 \times 10 = 502.4 \text{ cm}^3$$
Thể tích hình trụ B: $$V_B = \pi r_B^2 h_B = 3.14 \times 5^2 \times 8$$ $$= 3.14 \times 25 \times 8 = 628 \text{ cm}^3$$
So sánh: $V_B = 628 > 502.4 = V_A$
Kết luận: Hình trụ B có thể tích lớn hơn.
Dạng 7: Tính chi phí vật liệu
Bài 7: Làm một thùng đựng dầu hình trụ bằng tôn (kín cả hai đầu), có đường kính 80cm và chiều cao 1.2m. a) Tính diện tích tôn cần dùng b) Tính chi phí làm thùng nếu 1m² tôn giá 150,000 đồng
Lời giải:
Đổi đơn vị về cùng hệ:
- Đường kính: $d = 80$ cm $= 0.8$ m
- Bán kính: $r = \frac{0.8}{2} = 0.4$ m
- Chiều cao: $h = 1.2$ m
Câu a) Diện tích tôn:
Vì thùng kín cả hai đầu nên tính diện tích toàn phần: $$S_{tp} = 2\pi r(h + r) = 2 \times 3.14 \times 0.4 \times (1.2 + 0.4)$$ $$= 2 \times 3.14 \times 0.4 \times 1.6$$ $$= 4.0192 \text{ m}^2$$
Câu b) Chi phí: $$\text{Chi phí} = 4.0192 \times 150000 = 602880 \text{ đồng}$$
Làm tròn: Khoảng 603,000 đồng.
Đáp số:
- a) Diện tích tôn: 4.0192 m² ≈ 4.02 m²
- b) Chi phí: 602,880 đồng ≈ 603,000 đồng
X. MẸO VÀ LƯU Ý KHI TÍNH TOÁN
1. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm lẫn bán kính và đường kính
Sai:
- Đề cho đường kính $d = 10$ cm
- Tính thẳng: $V = \pi \times 10^2 \times h$ ❌ (sai vì dùng d thay cho r)
Đúng:
- Tính bán kính trước: $r = \frac{d}{2} = 5$ cm
- Rồi tính: $V = \pi \times 5^2 \times h$ ✓
❌ SAI LẦM 2: Quên nhân với 2 khi tính diện tích hai đáy
Sai:
- $S_{tp} = S_{xq} + S_{đáy}$ ❌ (thiếu một đáy)
Đúng:
- $S_{tp} = S_{xq} + 2S_{đáy}$ ✓ (có số 2)
❌ SAI LẦM 3: Nhầm đơn vị diện tích và thể tích
Sai:
- Diện tích: 100 cm ❌ (thiếu bình phương)
- Thể tích: 500 m² ❌ (sai đơn vị)
Đúng:
- Diện tích: 100 cm² ✓
- Thể tích: 500 cm³ hoặc 500 lít ✓
❌ SAI LẦM 4: Quên đổi đơn vị về cùng hệ
Sai:
- $r = 5$ cm, $h = 2$ m
- Tính thẳng: $V = 3.14 \times 5^2 \times 2$ ❌ (khác đơn vị)
Đúng:
- Đổi: $h = 2$ m $= 200$ cm
- Tính: $V = 3.14 \times 5^2 \times 200$ ✓
2. Mẹo nhớ công thức
Thể tích hình trụ:
“Diện tích đáy nhân chiều cao”
$$V = S_{đáy} \times h = \pi r^2 h$$
Nghĩ đơn giản: Lấy diện tích đáy nhân với chiều cao là ra thể tích.
Diện tích xung quanh:
“Chu vi đáy nhân chiều cao”
$$S_{xq} = C_{đáy} \times h = 2\pi r \times h$$
Tưởng tượng: Cắt và trải phẳng mặt xung quanh thành hình chữ nhật.
Diện tích toàn phần:
“Xung quanh cộng hai đáy”
$$S_{tp} = S_{xq} + 2S_{đáy}$$
Nhớ: Toàn bộ = Mặt cong + Hai mặt phẳng
3. Các bước giải bài tập hình trụ
Bước 1: Đọc kỹ đề, gạch chân số liệu
- Xác định rõ: r, d, h, V, S…
- Nếu cho d → tính ngay $r = \frac{d}{2}$
- Nếu cho đường kính → đổi sang bán kính ngay
Bước 2: Đổi đơn vị về cùng hệ
- Ví dụ: m → cm, cm → m
- Thể tích: cm³ → lít, lít → m³
- Quy tắc: Tất cả cùng đơn vị trước khi tính
Bước 3: Xác định công thức cần dùng
- Tính diện tích → dùng công thức $S$
- Tính thể tích → dùng công thức $V$
- Tính ngược → biến đổi công thức
Bước 4: Thay số và tính toán
- Cẩn thận với phép tính bình phương: $r^2$
- Cẩn thận với phép nhân nhiều số
- Sử dụng máy tính bỏ túi nếu cần
Bước 5: Viết đáp số đầy đủ đơn vị
- Diện tích → cm², m², dm²
- Thể tích → cm³, m³, dm³, lít
- Độ dài → cm, m, dm
4. Kiểm tra kết quả
Các điều kiện hợp lý:
- Thể tích phải > 0
- Bán kính, chiều cao phải > 0
- Diện tích toàn phần > Diện tích xung quanh
- $S_{tp} = S_{xq} + 2S_{đáy}$ (kiểm tra lại)
So sánh với thực tế:
- Lon nước ngọt: thường 330ml = 330 cm³
- Bể nước gia đình: vài m³ đến chục m³
- Cột nhà: chiều cao vài mét
Kiểm tra đơn vị:
- Diện tích phải có ²
- Thể tích phải có ³
- Không được lẫn lộn
5. Giá trị π cần nhớ
Các dạng giá trị π:
- $\pi \approx 3.14$ (chính xác 2 chữ số, dùng phổ biến nhất)
- $\pi = \frac{22}{7}$ (dạng phân số, dễ tính nhẩm)
- Trên máy tính: Dùng phím $\pi$ để chính xác hơn
Khi nào dùng giá trị nào:
- Đề bài yêu cầu $\pi = 3.14$ → dùng 3.14
- Đề bài yêu cầu $\pi = \frac{22}{7}$ → dùng phân số
- Đề không nói gì → dùng 3.14 hoặc để $\pi$
- Máy tính cho phép → dùng phím $\pi$ chính xác nhất
6. Quy đổi đơn vị nhanh
Độ dài:
- 1 m = 100 cm = 10 dm
- 1 dm = 10 cm = 0.1 m
- 1 cm = 0.01 m = 0.1 dm
Diện tích:
- 1 m² = 10000 cm² = 100 dm²
- 1 dm² = 100 cm² = 0.01 m²
- 1 cm² = 0.0001 m² = 0.01 dm²
Thể tích:
- 1 m³ = 1000 dm³ = 1000000 cm³ = 1000 lít
- 1 dm³ = 1000 cm³ = 1 lít = 0.001 m³
- 1 cm³ = 0.001 dm³ = 0.001 lít = 1 ml
- 1 lít = 1 dm³ = 1000 cm³ = 0.001 m³
Mẹo nhớ quy đổi:
- Độ dài: nhân/chia 10
- Diện tích: nhân/chia 100 (vì có ²)
- Thể tích: nhân/chia 1000 (vì có ³)
7. Lưu ý đặc biệt
Khi bài toán nói “không có nắp” hoặc “hở đáy”:
- Chỉ tính: $S = S_{xq} + S_{đáy}$ (một đáy)
- Không dùng công thức $S_{tp}$
Khi bài toán nói “kín”, “có nắp”, “toàn bộ bề mặt”:
- Tính: $S_{tp} = S_{xq} + 2S_{đáy}$
- Hoặc dùng: $S_{tp} = 2\pi r(h + r)$
Khi tính thể tích chất lỏng:
- Nếu “đầy bể” → $V = \pi r^2 h$ (toàn bộ)
- Nếu “cao $x$ cm” → $V = \pi r^2 x$ (chiều cao nước thay cho h)
Khi tính chi phí:
- Chi phí = Diện tích × Đơn giá
- Hoặc: Chi phí = Thể tích × Đơn giá
- Chú ý đơn vị: m² hay cm², m³ hay lít
XI. KẾT LUẬN
Bài viết đã tổng hợp đầy đủ và chi tiết các công thức về hình trụ, từ cơ bản đến nâng cao:
Các thành phần cơ bản của hình trụ:
- Hai đáy hình tròn bằng nhau
- Mặt xung quanh (mặt cong)
- Bán kính (r), đường kính (d), chiều cao (h)
- Mối quan hệ: $d = 2r$, $l = h$ (hình trụ tròn)
Công thức diện tích:
- Diện tích đáy: $S_{đáy} = \pi r^2$
- Diện tích xung quanh: $S_{xq} = 2\pi rh$
- Diện tích toàn phần: $S_{tp} = 2\pi r(h + r)$
Công thức thể tích:
- $V = \pi r^2 h$ (công thức quan trọng nhất)
Công thức tính ngược:
- Tính $r$ khi biết $V, h$ hoặc $S_{xq}, h$
- Tính $h$ khi biết $V, r$ hoặc $S_{xq}, r$
- Các công thức biến đổi linh hoạt
Bài tập mẫu:
- 7 dạng bài tập từ cơ bản đến nâng cao
- Lời giải chi tiết từng bước
- Ứng dụng thực tế: bể nước, lon sữa, thùng dầu
Mẹo và lưu ý:
- Cảnh báo các sai lầm thường gặp
- Mẹo nhớ công thức dễ dàng
- Quy trình giải bài tập chuẩn
- Quy đổi đơn vị nhanh
Tài liệu tham khảo và học thêm
Các chủ đề liên quan nên học:
Hình học không gian cơ bản:
- [Công thức hình nón – Diện tích và thể tích đầy đủ]
- [Công thức hình cầu – Bảng tổng hợp chi tiết]
- [Công thức hình hộp chữ nhật – Thể tích và diện tích]
- [Công thức hình chóp – Đầy đủ các loại]
- [Công thức hình lăng trụ – Tổng hợp công thức]

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa