Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ LỰC ĐÀN HỒI
- 1. Lực đàn hồi là gì?
- 2. Đặc điểm lực đàn hồi
- 3. Phân biệt Lớp 10 và Lớp 12
- II. ĐỊNH LUẬT HOOKE – CÔNG THỨC CƠ BẢN
- 1. Định luật Hooke
- 2. Các đại lượng trong công thức
- 3. Ví dụ minh họa cơ bản
- 4. Giới hạn đàn hồi
- III. CÔNG THỨC TÍNH ĐỘ DÃN CỦA LÒ XO
- 1. Từ định luật Hooke
- 2. Lò xo treo thẳng đứng cân bằng
- 3. Lò xo trên mặt phẳng nghiêng
- 4. Công thức chiều dài lò xo
- IV. CÔNG THỨC TÍNH ĐỘ CỨNG CỦA LÒ XO
- 1. Từ định luật Hooke
- 2. Từ vật treo cân bằng
- 3. Từ chu kỳ dao động (Lớp 12)
- 4. Công thức tổng hợp lò xo
- V. LỰC ĐÀN HỒI TRONG DAO ĐỘNG ĐIỀU HÒA (LỚP 12)
- 1. Phương trình dao động
- 2. Lực đàn hồi tại vị trí bất kỳ
- 3. Lực hồi phục
- 4. Điều kiện lò xo không rời vật
- 5. Năng lượng trong dao động điều hòa
- VI. BẢNG CÔNG THỨC TÓM TẮT
- A. Công thức cơ bản (Lớp 10)
- B. Lò xo ghép
- C. Dao động điều hòa (Lớp 12)
- D. Các trường hợp đặc biệt
- VII. BÀI TẬP MẪU
- VIII. PHƯƠNG PHÁP GIẢI NHANH
- 1. Dạng bài tính lực đàn hồi
- 2. Dạng bài tính độ cứng
- 3. Mẹo nhớ công thức
- IX. MẸO VÀ LƯU Ý
- 1. Các sai lầm thường gặp
- 2. Lưu ý quan trọng
- 3. Đơn vị cần nhớ
- X. KẾT LUẬN
- Công thức quan trọng nhất
I. GIỚI THIỆU VỀ LỰC ĐÀN HỒI
1. Lực đàn hồi là gì?
Định nghĩa: Lực đàn hồi là lực xuất hiện trong vật đàn hồi khi vật bị biến dạng (dãn hoặc nén), có xu hướng đưa vật trở về hình dạng ban đầu.
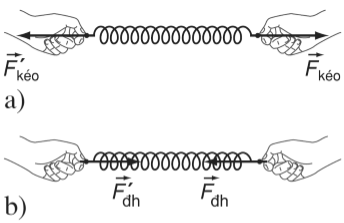
Ví dụ thực tế:
- Lò xo: Khi kéo hoặc nén lò xo, lực đàn hồi xuất hiện để đưa lò xo về chiều dài ban đầu
- Dây cao su: Khi kéo căng dây cao su, lực đàn hồi kéo dây co lại
- Thanh thép: Khi uốn cong thanh thép, lực đàn hồi có xu hướng làm thanh thẳng lại
- Bóng đàn hồi: Khi ép bóng, lực đàn hồi làm bóng nảy ra
Ký hiệu:
- $\vec{F}_{đh}$ hoặc $\vec{F}$ (lực đàn hồi)
- $\vec{F}_{lx}$ (lực lò xo)
2. Đặc điểm lực đàn hồi
Đặc điểm 1 – Hướng:
- Lực đàn hồi luôn có chiều ngược với chiều biến dạng
- Nếu lò xo bị kéo dãn → lực đàn hồi hướng vào trong (có xu hướng kéo lò xo co lại)
- Nếu lò xo bị nén → lực đàn hồi hướng ra ngoài (có xu hướng đẩy lò xo dãn ra)
Đặc điểm 2 – Độ lớn:
- Tỷ lệ thuận với độ biến dạng (trong giới hạn đàn hồi)
- Biến dạng càng lớn → lực đàn hồi càng lớn
- Được mô tả bởi định luật Hooke
Đặc điểm 3 – Điểm đặt:
- Tại điểm tiếp xúc giữa vật đàn hồi với vật khác
- Ví dụ: Điểm nối giữa lò xo và vật treo
3. Phân biệt Lớp 10 và Lớp 12
Lực đàn hồi được học ở hai cấp độ khác nhau:
| Nội dung | Vật lý 10 | Vật lý 12 |
|---|---|---|
| Lực đàn hồi tĩnh | ✅ Học chi tiết | ✅ Ôn lại |
| Định luật Hooke | ✅ Trọng tâm | ✅ Áp dụng |
| Vật cân bằng | ✅ Học kỹ | ✅ Ứng dụng |
| Dao động điều hòa | ❌ Chưa học | ✅ Trọng tâm |
| Năng lượng | Cơ bản | Chi tiết |
| Chu kỳ, tần số | ❌ Chưa học | ✅ Học kỹ |
Lớp 10: Tập trung vào lực đàn hồi trong trạng thái cân bằng (vật đứng yên)
Lớp 12: Tập trung vào lực đàn hồi trong dao động điều hòa (vật dao động)
II. ĐỊNH LUẬT HOOKE – CÔNG THỨC CƠ BẢN
1. Định luật Hooke
Phát biểu: Trong giới hạn đàn hồi, độ lớn lực đàn hồi của lò xo tỷ lệ thuận với độ biến dạng của lò xo.
Công thức dạng độ lớn:
$$\boxed{F_{đh} = k \cdot |\Delta l|}$$
Công thức dạng vectơ:
$$\boxed{\vec{F}_{đh} = -k \cdot \Delta \vec{l}}$$
Trong đó:
- $F_{đh}$: Độ lớn lực đàn hồi (N – Newton)
- $k$: Độ cứng của lò xo (N/m)
- $|\Delta l|$: Độ biến dạng (độ dãn hoặc độ nén) của lò xo (m – mét)
- $\Delta l = l – l_0$ với:
- $l$: Chiều dài lò xo khi có biến dạng
- $l_0$: Chiều dài tự nhiên (không biến dạng)
Ý nghĩa dấu âm trong công thức vectơ:
- Dấu âm chỉ rằng lực đàn hồi luôn ngược chiều với độ biến dạng
- Nếu lò xo dãn ($\Delta l > 0$) → $\vec{F}_{đh}$ hướng về vị trí ban đầu (co lại)
- Nếu lò xo nén ($\Delta l < 0$) → $\vec{F}_{đh}$ hướng ra ngoài (dãn ra)
2. Các đại lượng trong công thức
a) Độ cứng k
Định nghĩa: Độ cứng k là đại lượng đặc trưng cho khả năng chống lại biến dạng của lò xo.
Ý nghĩa vật lý:
- $k$ lớn → lò xo cứng → khó biến dạng → cần lực lớn để kéo dãn
- $k$ nhỏ → lò xo mềm → dễ biến dạng → cần lực nhỏ để kéo dãn
Đơn vị: N/m (Newton trên mét)
Phụ thuộc vào:
- Vật liệu làm lò xo (thép, đồng, nhựa…)
- Kích thước lò xo (đường kính vòng xo, đường kính dây xo)
- Số vòng xo
- Chiều dài lò xo
Lưu ý: Với cùng một lò xo, độ cứng k không đổi (không phụ thuộc vào lực tác dụng hay độ biến dạng).
b) Độ biến dạng $\Delta l$
Định nghĩa: Độ biến dạng là độ thay đổi chiều dài của lò xo so với chiều dài tự nhiên.
Công thức: $$\Delta l = l – l_0$$
Các trường hợp:
- $\Delta l > 0$: Lò xo bị dãn (kéo căng)
- $\Delta l < 0$: Lò xo bị nén (ép lại)
- $\Delta l = 0$: Lò xo ở trạng thái tự nhiên (không biến dạng, $F_{đh} = 0$)
Đơn vị: mét (m), hoặc cm, mm (cần đổi sang m khi tính)
c) Chiều dài lò xo
$l_0$ – Chiều dài tự nhiên:
- Chiều dài lò xo khi không chịu lực tác dụng
- Không có biến dạng
- Lực đàn hồi bằng 0
$l$ – Chiều dài khi có biến dạng:
- Chiều dài lò xo khi đang chịu lực
- $l > l_0$: lò xo dãn
- $l < l_0$: lò xo nén
- $l = l_0$: lò xo tự nhiên
Mối liên hệ: $$l = l_0 + \Delta l$$
3. Ví dụ minh họa cơ bản
Ví dụ 1: Một lò xo có độ cứng $k = 100$ N/m và chiều dài tự nhiên $l_0 = 20$ cm. Kéo lò xo đến chiều dài $l = 25$ cm. Tính lực đàn hồi của lò xo?
Lời giải:
Bước 1: Tính độ dãn của lò xo $$\Delta l = l – l_0 = 25 – 20 = 5 \text{ cm} = 0.05 \text{ m}$$
Bước 2: Áp dụng định luật Hooke $$F_{đh} = k \cdot |\Delta l| = 100 \times 0.05 = 5 \text{ N}$$
Đáp án: Lực đàn hồi của lò xo là 5N.
Ví dụ 2: Lò xo có $k = 200$ N/m, $l_0 = 30$ cm. Nén lò xo xuống còn 25 cm. Tính lực đàn hồi?
Lời giải:
Bước 1: Tính độ nén $$\Delta l = l – l_0 = 25 – 30 = -5 \text{ cm} = -0.05 \text{ m}$$
Bước 2: Tính lực đàn hồi $$F_{đh} = k \cdot |\Delta l| = 200 \times |-0.05| = 200 \times 0.05 = 10 \text{ N}$$
Đáp án: Lực đàn hồi là 10N (hướng đẩy lò xo dãn ra).
4. Giới hạn đàn hồi
Khái niệm: Giới hạn đàn hồi là giới hạn mà khi vượt qua, vật không thể trở về hình dạng ban đầu.
Lưu ý quan trọng:
✅ Định luật Hooke chỉ đúng trong giới hạn đàn hồi
❌ Nếu kéo lò xo quá mạnh (vượt giới hạn đàn hồi):
- Lò xo bị biến dạng vĩnh viễn (không co lại được)
- Định luật Hooke không còn đúng
- Lò xo có thể bị hỏng hoặc gãy
Ví dụ: Kéo lò xo quá mạnh → lò xo bị dãn vĩnh viễn → chiều dài tự nhiên mới lớn hơn $l_0$ ban đầu.
III. CÔNG THỨC TÍNH ĐỘ DÃN CỦA LÒ XO
1. Từ định luật Hooke
Từ công thức $F_{đh} = k \cdot |\Delta l|$, ta suy ra:
$$\boxed{\Delta l = \frac{F_{đh}}{k}}$$
Ví dụ: Tác dụng lực $F = 20$ N lên lò xo có độ cứng $k = 200$ N/m. Tính độ dãn?
Lời giải: $$\Delta l = \frac{F}{k} = \frac{20}{200} = 0.1 \text{ m} = 10 \text{ cm}$$
Đáp án: Lò xo dãn ra 10 cm.
2. Lò xo treo thẳng đứng cân bằng
Bài toán: Treo vật có khối lượng $m$ vào lò xo thẳng đứng. Khi vật đứng yên (cân bằng), tính độ dãn của lò xo?
Phân tích:
- Vật chịu hai lực: trọng lực $\vec{P}$ (hướng xuống) và lực đàn hồi $\vec{F}_{đh}$ (hướng lên)
- Vật cân bằng: $\vec{F}_{đh} + \vec{P} = \vec{0}$
- Chiếu lên phương thẳng đứng: $F_{đh} = P = mg$
Công thức:
$$\boxed{\Delta l_0 = \frac{mg}{k}}$$
Trong đó:
- $\Delta l_0$: Độ dãn của lò xo tại vị trí cân bằng
- $m$: Khối lượng vật (kg)
- $g$: Gia tốc trọng trường ($g = 10$ m/s² hoặc 9.8 m/s²)
- $k$: Độ cứng lò xo (N/m)
Ví dụ 3: Treo vật có khối lượng $m = 0.5$ kg vào lò xo có độ cứng $k = 100$ N/m. Tính độ dãn của lò xo khi vật cân bằng? (Lấy $g = 10$ m/s²)
Lời giải: $$\Delta l_0 = \frac{mg}{k} = \frac{0.5 \times 10}{100} = \frac{5}{100} = 0.05 \text{ m} = 5 \text{ cm}$$
Đáp án: Lò xo dãn ra 5 cm.
3. Lò xo trên mặt phẳng nghiêng
Bài toán: Vật khối lượng $m$ nằm trên mặt phẳng nghiêng góc $\alpha$, nối với lò xo song song với mặt phẳng. Khi vật cân bằng, tính độ dãn?
Phân tích:
- Thành phần trọng lực theo mặt phẳng nghiêng: $P_t = mg\sin\alpha$
- Cân bằng: $F_{đh} = P_t = mg\sin\alpha$
Công thức:
$$\boxed{\Delta l = \frac{mg\sin\alpha}{k}}$$
Ví dụ 4: Vật $m = 1$ kg trên mặt phẳng nghiêng $\alpha = 30°$, nối với lò xo $k = 50$ N/m. Tính độ dãn? (Lấy $g = 10$ m/s², $\sin 30° = 0.5$)
Lời giải: $$\Delta l = \frac{mg\sin\alpha}{k} = \frac{1 \times 10 \times 0.5}{50} = \frac{5}{50} = 0.1 \text{ m} = 10 \text{ cm}$$
Đáp án: Lò xo dãn 10 cm.
4. Công thức chiều dài lò xo
Khi biết độ dãn, ta có thể tính chiều dài lò xo:
$$\boxed{l = l_0 + \Delta l}$$
Hoặc với vật treo cân bằng:
$$\boxed{l = l_0 + \frac{F}{k} = l_0 + \frac{mg}{k}}$$
Ví dụ 5: Lò xo có $l_0 = 20$ cm, $k = 100$ N/m. Treo vật $m = 0.3$ kg. Tính chiều dài lò xo khi cân bằng?
Lời giải:
Cách 1: Tính từng bước
- $\Delta l = \frac{0.3 \times 10}{100} = 0.03$ m = 3 cm
- $l = 20 + 3 = 23$ cm
Cách 2: Dùng công thức trực tiếp $$l = l_0 + \frac{mg}{k} = 0.2 + \frac{0.3 \times 10}{100} = 0.2 + 0.03 = 0.23 \text{ m} = 23 \text{ cm}$$
Đáp án: 23 cm.
IV. CÔNG THỨC TÍNH ĐỘ CỨNG CỦA LÒ XO
1. Từ định luật Hooke
Từ $F_{đh} = k \cdot \Delta l$, ta suy ra:
$$\boxed{k = \frac{F_{đh}}{\Delta l}}$$
Ví dụ 6: Tác dụng lực $F = 30$ N làm lò xo dãn $\Delta l = 15$ cm. Tính độ cứng?
Lời giải: $$k = \frac{F}{\Delta l} = \frac{30}{0.15} = 200 \text{ N/m}$$
Đáp án: Độ cứng $k = 200$ N/m.
2. Từ vật treo cân bằng
Khi treo vật cân bằng, ta có:
$$\boxed{k = \frac{mg}{\Delta l_0}}$$
Ví dụ 7: Treo vật khối lượng $m = 200$ g vào lò xo làm lò xo dãn $\Delta l_0 = 4$ cm. Tính độ cứng? (Lấy $g = 10$ m/s²)
Lời giải: $$k = \frac{mg}{\Delta l_0} = \frac{0.2 \times 10}{0.04} = \frac{2}{0.04} = 50 \text{ N/m}$$
Đáp án: Độ cứng $k = 50$ N/m.
3. Từ chu kỳ dao động (Lớp 12)
Trong dao động điều hòa của con lắc lò xo, chu kỳ dao động được tính theo công thức:
$$T = 2\pi\sqrt{\frac{m}{k}}$$
Từ đó suy ra độ cứng:
$$\boxed{k = \frac{4\pi^2 m}{T^2}}$$
Ví dụ 8: Con lắc lò xo có khối lượng $m = 0.1$ kg dao động với chu kỳ $T = 0.628$ s. Tính độ cứng? (Lấy $\pi \approx 3.14$)
Lời giải: $$k = \frac{4\pi^2 m}{T^2} = \frac{4 \times 3.14^2 \times 0.1}{0.628^2} = \frac{3.95}{0.394} \approx 10 \text{ N/m}$$
Đáp án: Độ cứng khoảng 10 N/m.
4. Công thức tổng hợp lò xo
Khi ghép nhiều lò xo, độ cứng tương đương phụ thuộc vào cách ghép:
a) Ghép nối tiếp
Công thức:
$$\boxed{\frac{1}{k} = \frac{1}{k_1} + \frac{1}{k_2} + … + \frac{1}{k_n}}$$
Với 2 lò xo:
$$k = \frac{k_1 k_2}{k_1 + k_2}$$
Đặc điểm:
- Độ cứng tương đương nhỏ hơn độ cứng từng lò xo
- Lò xo trở nên mềm hơn
Ví dụ 9: Hai lò xo $k_1 = 100$ N/m và $k_2 = 100$ N/m ghép nối tiếp. Tính $k$?
Lời giải: $$k = \frac{k_1 k_2}{k_1 + k_2} = \frac{100 \times 100}{100 + 100} = \frac{10000}{200} = 50 \text{ N/m}$$
Đáp án: $k = 50$ N/m (nhỏ hơn cả hai).
b) Ghép song song
Công thức:
$$\boxed{k = k_1 + k_2 + … + k_n}$$
Đặc điểm:
- Độ cứng tương đương lớn hơn độ cứng từng lò xo
- Lò xo trở nên cứng hơn
Ví dụ 10: Hai lò xo $k_1 = 100$ N/m và $k_2 = 100$ N/m ghép song song. Tính $k$?
Lời giải: $$k = k_1 + k_2 = 100 + 100 = 200 \text{ N/m}$$
Đáp án: $k = 200$ N/m (lớn hơn cả hai).
V. LỰC ĐÀN HỒI TRONG DAO ĐỘNG ĐIỀU HÒA (LỚP 12)
1. Phương trình dao động
Vật gắn với lò xo dao động điều hòa theo phương trình:
$$\boxed{x = A\cos(\omega t + \varphi)}$$
Trong đó:
- $x$: Li độ (m) – khoảng cách từ vật đến vị trí cân bằng
- $A$: Biên độ dao động (m) – li độ cực đại
- $\omega$: Tần số góc (rad/s) $$\omega = \sqrt{\frac{k}{m}}$$
- $t$: Thời gian (s)
- $\varphi$: Pha ban đầu (rad)
Các đại lượng liên quan:
Chu kỳ: $T = 2\pi\sqrt{\frac{m}{k}}$ (s)
Tần số: $f = \frac{1}{T} = \frac{1}{2\pi}\sqrt{\frac{k}{m}}$ (Hz)
2. Lực đàn hồi tại vị trí bất kỳ
Tại vị trí có li độ $x$ (tính từ vị trí cân bằng):
Nếu tính từ vị trí tự nhiên của lò xo:
$$\boxed{F = k(x + \Delta l_0)}$$
Nếu tính từ vị trí cân bằng (thường dùng):
$$\boxed{F = k|x + \Delta l_0|}$$
Các vị trí đặc biệt:
Tại vị trí cân bằng ($x = 0$): $$F_0 = k\Delta l_0 = mg$$
Tại biên trên ($x = A$): $$F_{min} = k(A – \Delta l_0) = k|A – \Delta l_0|$$
Nếu $A < \Delta l_0$: $F_{min} = k(\Delta l_0 – A)$
Tại biên dưới ($x = -A$): $$F_{max} = k(A + \Delta l_0)$$
3. Lực hồi phục
Định nghĩa: Lực hồi phục là lực luôn hướng về vị trí cân bằng, gây ra dao động điều hòa.
Công thức:
$$\boxed{F_{hp} = -kx}$$
Đặc điểm:
- Luôn hướng về vị trí cân bằng (VTCB)
- Độ lớn tỷ lệ với li độ: $|F_{hp}| = k|x|$
- Là nguyên nhân gây ra dao động điều hòa
Phân biệt lực hồi phục và lực đàn hồi:
- Lực hồi phục: Được tính từ VTCB, gây ra dao động
- Lực đàn hồi: Được tính từ vị trí tự nhiên của lò xo
4. Điều kiện lò xo không rời vật
Bài toán: Lò xo treo thẳng đứng dao động. Tìm biên độ tối đa để lò xo không rời khỏi vật?
Phân tích: Lò xo rời vật khi lực đàn hồi bằng 0, tức là tại biên trên:
$$F_{min} = k(\Delta l_0 – A) = 0$$
Điều kiện: $A \leq \Delta l_0$
Công thức:
$$\boxed{A_{max} = \Delta l_0 = \frac{mg}{k}}$$
Ví dụ 11: Con lắc lò xo treo thẳng đứng, khi cân bằng lò xo dãn $\Delta l_0 = 5$ cm. Tính biên độ dao động tối đa để lò xo không rời vật?
Lời giải: $$A_{max} = \Delta l_0 = 5 \text{ cm}$$
Đáp án: Biên độ tối đa là 5 cm.
5. Năng lượng trong dao động điều hòa
a) Thế năng đàn hồi
Tại vị trí có li độ $x$:
$$\boxed{W_t = \frac{1}{2}kx^2}$$
Đặc điểm:
- Tại VTCB ($x = 0$): $W_t = 0$ (thế năng cực tiểu)
- Tại biên ($x = \pm A$): $W_t = \frac{1}{2}kA^2$ (thế năng cực đại)
b) Động năng
Với vận tốc $v$:
$$W_đ = \frac{1}{2}mv^2$$
Hoặc theo li độ:
$$\boxed{W_đ = \frac{1}{2}k(A^2 – x^2)}$$
Đặc điểm:
- Tại VTCB ($x = 0$): $W_đ = \frac{1}{2}kA^2$ (động năng cực đại)
- Tại biên ($x = \pm A$): $W_đ = 0$ (động năng cực tiểu)
c) Cơ năng
Định luật bảo toàn cơ năng:
$$\boxed{W = W_t + W_đ = \frac{1}{2}kA^2 = \text{const}}$$
Ý nghĩa: Cơ năng của dao động điều hòa không đổi theo thời gian (nếu không có ma sát).
Công thức khác: $$W = \frac{1}{2}kA^2 = \frac{1}{2}m\omega^2 A^2 = 2\pi^2 mf^2A^2$$
VI. BẢNG CÔNG THỨC TÓM TẮT
A. Công thức cơ bản (Lớp 10)
| Đại lượng | Công thức | Đơn vị |
|---|---|---|
| Lực đàn hồi | $F_{đh} = k \cdot |\Delta l|$ | N |
| Độ dãn | $\Delta l = \frac{F_{đh}}{k}$ | m |
| Độ dãn (vật treo) | $\Delta l_0 = \frac{mg}{k}$ | m |
| Độ cứng | $k = \frac{F_{đh}}{\Delta l}$ | N/m |
| Độ cứng (vật treo) | $k = \frac{mg}{\Delta l_0}$ | N/m |
| Chiều dài | $l = l_0 + \Delta l$ | m |
B. Lò xo ghép
| Loại ghép | Công thức | Đặc điểm |
|---|---|---|
| Nối tiếp | $\frac{1}{k} = \frac{1}{k_1} + \frac{1}{k_2}$ | $k < k_1, k_2$ (mềm hơn) |
| Nối tiếp (2 lò xo) | $k = \frac{k_1 k_2}{k_1 + k_2}$ | Nhỏ hơn cả hai |
| Song song | $k = k_1 + k_2$ | $k > k_1, k_2$ (cứng hơn) |
C. Dao động điều hòa (Lớp 12)
| Đại lượng | Công thức | Đơn vị |
|---|---|---|
| Tần số góc | $\omega = \sqrt{\frac{k}{m}}$ | rad/s |
| Chu kỳ | $T = 2\pi\sqrt{\frac{m}{k}}$ | s |
| Tần số | $f = \frac{1}{2\pi}\sqrt{\frac{k}{m}}$ | Hz |
| Độ cứng (từ T) | $k = \frac{4\pi^2 m}{T^2}$ | N/m |
| Lực hồi phục | $F_{hp} = -kx$ | N |
| Thế năng | $W_t = \frac{1}{2}kx^2$ | J |
| Động năng | $W_đ = \frac{1}{2}k(A^2-x^2)$ | J |
| Cơ năng | $W = \frac{1}{2}kA^2$ | J |
| Điều kiện không rời | $A_{max} = \frac{mg}{k}$ | m |
D. Các trường hợp đặc biệt
| Tình huống | Công thức độ dãn |
|---|---|
| Treo thẳng đứng | $\Delta l_0 = \frac{mg}{k}$ |
| Mặt ngang | $\Delta l = 0$ (nếu không kéo) |
| Mặt nghiêng $\alpha$ | $\Delta l = \frac{mg\sin\alpha}{k}$ |
VII. BÀI TẬP MẪU
Bài 1: Tính lực đàn hồi
Đề bài: Lò xo có độ cứng $k = 50$ N/m bị kéo dãn $\Delta l = 8$ cm. Tính lực đàn hồi?
Lời giải:
Đổi đơn vị: $\Delta l = 8$ cm = 0.08 m
Áp dụng công thức: $$F_{đh} = k \cdot \Delta l = 50 \times 0.08 = 4 \text{ N}$$
Đáp án: Lực đàn hồi là 4N.
Bài 2: Tính độ cứng
Đề bài: Treo vật có khối lượng $m = 100$ g vào lò xo làm lò xo dãn $\Delta l = 2$ cm. Tính độ cứng? (Lấy $g = 10$ m/s²)
Lời giải:
Đổi đơn vị:
- $m = 100$ g = 0.1 kg
- $\Delta l = 2$ cm = 0.02 m
Áp dụng công thức: $$k = \frac{mg}{\Delta l_0} = \frac{0.1 \times 10}{0.02} = \frac{1}{0.02} = 50 \text{ N/m}$$
Đáp án: Độ cứng $k = 50$ N/m.
Bài 3: Tính độ dãn
Đề bài: Vật có khối lượng $m = 0.4$ kg treo vào lò xo có độ cứng $k = 80$ N/m. Tính độ dãn của lò xo khi vật cân bằng? (Lấy $g = 10$ m/s²)
Lời giải: $$\Delta l_0 = \frac{mg}{k} = \frac{0.4 \times 10}{80} = \frac{4}{80} = 0.05 \text{ m} = 5 \text{ cm}$$
Đáp án: Lò xo dãn 5 cm.
Bài 4: Lò xo ghép nối tiếp
Đề bài: Hai lò xo có độ cứng $k_1 = 60$ N/m và $k_2 = 40$ N/m được ghép nối tiếp. Tính độ cứng tương đương?
Lời giải:
Áp dụng công thức ghép nối tiếp: $$k = \frac{k_1 k_2}{k_1 + k_2} = \frac{60 \times 40}{60 + 40} = \frac{2400}{100} = 24 \text{ N/m}$$
Kiểm tra: $k = 24$ N/m < $k_1 = 60$ N/m và $k < k_2 = 40$ N/m ✓
Đáp án: Độ cứng tương đương là 24 N/m.
Bài 5: Tính chu kỳ dao động
Đề bài: Con lắc lò xo có khối lượng $m = 100$ g và độ cứng $k = 25$ N/m. Tính chu kỳ dao động? (Lấy $\pi = 3.14$)
Lời giải:
Đổi: $m = 0.1$ kg
Áp dụng công thức: $$T = 2\pi\sqrt{\frac{m}{k}} = 2 \times 3.14 \times \sqrt{\frac{0.1}{25}}$$ $$= 6.28 \times \sqrt{0.004} = 6.28 \times 0.063 \approx 0.4 \text{ s}$$
Đáp án: Chu kỳ dao động khoảng 0.4 giây.
Bài 6: Biên độ tối đa
Đề bài: Con lắc lò xo treo thẳng đứng, khi cân bằng lò xo dãn $\Delta l_0 = 5$ cm. Tính biên độ dao động tối đa để lò xo không rời khỏi vật?
Lời giải:
Áp dụng điều kiện không rời vật: $$A_{max} = \Delta l_0 = 5 \text{ cm}$$
Đáp án: Biên độ tối đa là 5 cm.
VIII. PHƯƠNG PHÁP GIẢI NHANH
1. Dạng bài tính lực đàn hồi
Quy trình 3 bước:
Bước 1: Xác định độ cứng $k$ và độ biến dạng $\Delta l$
- Đọc kỹ đề, ghi rõ giá trị đã cho
- Chú ý đổi đơn vị: cm → m
Bước 2: Áp dụng định luật Hooke $$F_{đh} = k \cdot |\Delta l|$$
Bước 3: Kiểm tra kết quả
- Đơn vị: Newton (N)
- Giá trị hợp lý: $F > 0$
2. Dạng bài tính độ cứng
Có 3 phương pháp tùy vào dữ kiện đề bài:
Phương pháp 1: Từ lực và độ dãn $$k = \frac{F}{\Delta l}$$
Phương pháp 2: Từ vật treo cân bằng $$k = \frac{mg}{\Delta l_0}$$
Phương pháp 3: Từ chu kỳ dao động (Lớp 12) $$k = \frac{4\pi^2 m}{T^2}$$
Chọn phương pháp phù hợp với dữ kiện đề bài cho!
3. Mẹo nhớ công thức
“F bằng k nhân delta l” – Định luật Hooke cơ bản
Treo thẳng đứng: Nhớ công thức $\Delta l_0 = \frac{mg}{k}$ (mg trên k)
Ghép lò xo:
- Nối tiếp: k giảm (nhỏ hơn cả hai) – “càng dài càng mềm”
- Song song: k tăng (lớn hơn cả hai) – “cộng lại”
Chu kỳ dao động: $T = 2\pi\sqrt{\frac{m}{k}}$ – “m trên k, có 2 pi”
Điều kiện không rời: $A_{max} = \Delta l_0$ – “biên độ max bằng độ dãn ban đầu”
IX. MẸO VÀ LƯU Ý
1. Các sai lầm thường gặp
❌ SAI LẦM 1: Quên đổi đơn vị cm → m
Sai: $k = 100$ N/m, $\Delta l = 5$ cm → $F = 100 \times 5 = 500$ N ❌
Đúng: Đổi $\Delta l = 5$ cm = 0.05 m → $F = 100 \times 0.05 = 5$ N ✓
❌ SAI LẦM 2: Nhầm $l$ với $\Delta l$
Sai: Cho $l_0 = 20$ cm, $l = 25$ cm → $F = k \times 25$ ❌
Đúng: Tính $\Delta l = l – l_0 = 25 – 20 = 5$ cm → $F = k \times \Delta l$ ✓
❌ SAI LẦM 3: Quên rằng $F_{đh}$ luôn ngược chiều biến dạng
Lưu ý:
- Lò xo dãn → $F_{đh}$ kéo về (co lại)
- Lò xo nén → $F_{đh}$ đẩy ra (dãn ra)
❌ SAI LẦM 4: Nhầm công thức ghép nối tiếp và song song
Nhớ:
- Nối tiếp: $\frac{1}{k} = \frac{1}{k_1} + \frac{1}{k_2}$ (có phân số)
- Song song: $k = k_1 + k_2$ (cộng thẳng)
2. Lưu ý quan trọng
Định luật Hooke chỉ đúng trong giới hạn đàn hồi
- Không kéo lò xo quá mạnh
- Vượt giới hạn → lò xo biến dạng vĩnh viễn
Độ cứng k không đổi với cùng một lò xo
- Không phụ thuộc lực tác dụng
- Không phụ thuộc độ biến dạng
Lực đàn hồi luôn hướng về vị trí ban đầu
- Có xu hướng đưa lò xo về trạng thái tự nhiên
Khi $\Delta l = 0$ thì $F_{đh} = 0$
- Lò xo ở trạng thái tự nhiên
- Không có lực đàn hồi
3. Đơn vị cần nhớ
| Đại lượng | Đơn vị | Ghi chú |
|---|---|---|
| Lực $F$ | N (Newton) | Đơn vị chuẩn |
| Độ cứng $k$ | N/m | Newton trên mét |
| Độ dãn $\Delta l$ | m (mét) | Hoặc cm (cần đổi) |
| Khối lượng $m$ | kg | Kilôgam |
| Chiều dài $l, l_0$ | m | Mét |
Quy tắc vàng: Luôn đổi tất cả về đơn vị chuẩn (N, m, kg) trước khi tính!
X. KẾT LUẬN
Bài viết đã trình bày đầy đủ và chi tiết các công thức lực đàn hồi:
Định luật Hooke (cơ bản nhất): $$F_{đh} = k \cdot |\Delta l|$$
Công thức độ dãn:
- Tổng quát: $\Delta l = \frac{F}{k}$
- Vật treo: $\Delta l_0 = \frac{mg}{k}$
Công thức độ cứng:
- Từ lực: $k = \frac{F}{\Delta l}$
- Từ vật treo: $k = \frac{mg}{\Delta l_0}$
- Từ chu kỳ: $k = \frac{4\pi^2 m}{T^2}$
Lò xo ghép:
- Nối tiếp: $k = \frac{k_1k_2}{k_1+k_2}$
- Song song: $k = k_1 + k_2$
Dao động điều hòa (Lớp 12):
- Chu kỳ: $T = 2\pi\sqrt{\frac{m}{k}}$
- Lực hồi phục: $F_{hp} = -kx$
- Cơ năng: $W = \frac{1}{2}kA^2$
- Điều kiện không rời: $A_{max} = \frac{mg}{k}$
Công thức quan trọng nhất
Định luật Hooke – Nền tảng mọi bài toán:
$$\boxed{F_{đh} = k \cdot |\Delta l|}$$
Công thức vàng cho vật treo:
$$\boxed{\Delta l_0 = \frac{mg}{k}}$$

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
