Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ TAM GIÁC VUÔNG
- 1. Tam giác vuông là gì?
- 2. Tam giác vuông học ở lớp mấy?
- II. CÔNG THỨC DIỆN TÍCH TAM GIÁC VUÔNG
- 1. Công thức diện tích cơ bản (Lớp 5)
- 2. Công thức diện tích khi biết cạnh huyền và đường cao (Lớp 8)
- 3. Công thức diện tích khi biết cạnh huyền và 1 cạnh góc vuông (Lớp 7)
- 4. Diện tích tam giác vuông lớn nhất khi nào?
- III. CÔNG THỨC TAM GIÁC VUÔNG CÂN
- 1. Đặc điểm tam giác vuông cân
- 2. Công thức diện tích tam giác vuông cân
- 3. Công thức chu vi tam giác vuông cân
- IV. CÔNG THỨC TÍNH CẠNH TAM GIÁC VUÔNG
- 1. Định lý Pitago (Lớp 7)
- Hệ quả – Công thức tính cạnh:
- 2. Công thức tính cạnh trong tam giác vuông cân
- 3. Bộ số Pitago thường gặp (Lớp 7)
- V. CÔNG THỨC CHU VI TAM GIÁC VUÔNG
- 1. Công thức chu vi cơ bản (Lớp 5)
- 2. Chu vi khi biết hai cạnh góc vuông (Lớp 7)
- 3. Chu vi tam giác vuông cân
- VI. BẢNG CÔNG THỨC TỔNG HỢP
- A. Công thức diện tích
- B. Công thức tính cạnh (Định lý Pitago)
- C. Công thức tam giác vuông cân
- D. Công thức chu vi
- VII. BÀI TẬP MẪU THEO LỚP
- VIII. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Kiểm tra nhanh
- 4. Quy trình giải bài tập
- IX. KẾT LUẬN
I. GIỚI THIỆU VỀ TAM GIÁC VUÔNG
1. Tam giác vuông là gì?
Định nghĩa: Tam giác vuông là tam giác có một góc vuông (góc 90°). Đây là một trong những hình học cơ bản và quan trọng nhất trong toán học.
Các thành phần của tam giác vuông:
- 2 cạnh góc vuông (thường ký hiệu là $a$ và $b$): Là hai cạnh tạo thành góc vuông
- 1 cạnh huyền (ký hiệu là $c$): Là cạnh đối diện với góc vuông, luôn là cạnh dài nhất trong tam giác
- 1 góc vuông: Góc 90° (thường đánh dấu bằng hình vuông nhỏ)
- 2 góc nhọn: Hai góc còn lại, có tổng bằng 90°
Hình minh họa:
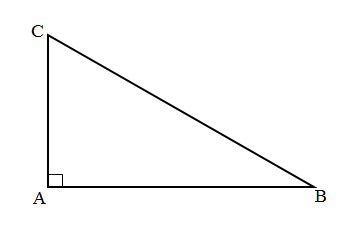
Đặc điểm quan trọng:
- Cạnh huyền luôn là cạnh dài nhất
- Hai góc nhọn có tổng bằng 90° (bù nhau)
- Thỏa mãn định lý Pitago: $a^2 + b^2 = c^2$
2. Tam giác vuông học ở lớp mấy?
Tam giác vuông là kiến thức xuyên suốt từ tiểu học đến THCS, với độ phức tạp tăng dần:
| Lớp | Nội dung học | Công thức chính |
|---|---|---|
| Lớp 5 | Diện tích, chu vi cơ bản | $S = \frac{ab}{2}$, $P = a+b+c$ |
| Lớp 7 | Định lý Pitago, tính cạnh, tam giác vuông cân | $c^2 = a^2 + b^2$ |
| Lớp 8 | Hệ thức lượng, đường cao, hình chiếu | $h^2 = ab’$, $bc’ = a^2$ |
| Lớp 9 | Tỉ số lượng giác, sin, cos, tan | $\sin A = \frac{a}{c}$ |
II. CÔNG THỨC DIỆN TÍCH TAM GIÁC VUÔNG
1. Công thức diện tích cơ bản (Lớp 5)
Công thức chính: Cho tam giác vuông có hai cạnh góc vuông là $a$ và $b$:
$$\boxed{S = \frac{1}{2}ab}$$
Hoặc viết dưới dạng:
$$\boxed{S = \frac{a \times b}{2}}$$
Trong đó:
- $S$: Diện tích tam giác (đơn vị: cm², m², dm², mm²…)
- $a$, $b$: Độ dài hai cạnh góc vuông (đơn vị: cm, m, dm, mm…)
Cách nhớ: “Nhân hai cạnh góc vuông rồi chia đôi”
Giải thích: Tam giác vuông bằng nửa hình chữ nhật có hai cạnh là $a$ và $b$, nên diện tích bằng một nửa diện tích hình chữ nhật đó.
Ví dụ 1: Tam giác vuông có hai cạnh góc vuông lần lượt là 3cm và 4cm. Tính diện tích?
Lời giải: $$S = \frac{a \times b}{2} = \frac{3 \times 4}{2} = \frac{12}{2} = 6 \text{ cm}^2$$
Kết luận: Diện tích tam giác vuông là 6 cm².
2. Công thức diện tích khi biết cạnh huyền và đường cao (Lớp 8)
Công thức: Cho tam giác vuông có:
- Cạnh huyền: $c$
- Đường cao ứng với cạnh huyền: $h$
$$\boxed{S = \frac{1}{2}ch}$$
Cách nhớ: Giống như công thức diện tích tam giác thường: “Một nửa tích của đáy và chiều cao”
Ví dụ 2: Tam giác vuông có cạnh huyền 10cm, đường cao ứng với cạnh huyền là 4.8cm. Tính diện tích?
Lời giải: $$S = \frac{c \times h}{2} = \frac{10 \times 4.8}{2} = \frac{48}{2} = 24 \text{ cm}^2$$
Kết luận: Diện tích tam giác là 24 cm².
3. Công thức diện tích khi biết cạnh huyền và 1 cạnh góc vuông (Lớp 7)
Cho: Cạnh huyền $c$ và một cạnh góc vuông $a$
Phương pháp giải:
Bước 1: Tính cạnh góc vuông còn lại bằng định lý Pitago: $$b = \sqrt{c^2 – a^2}$$
Bước 2: Tính diện tích: $$S = \frac{1}{2}ab = \frac{1}{2}a\sqrt{c^2 – a^2}$$
Hoặc công thức rút gọn:
$$\boxed{S = \frac{a\sqrt{c^2 – a^2}}{2}}$$
Ví dụ 3: Tam giác vuông có cạnh huyền 5cm, một cạnh góc vuông 3cm. Tính diện tích?
Lời giải:
Bước 1: Tính cạnh góc vuông còn lại: $$b = \sqrt{c^2 – a^2} = \sqrt{5^2 – 3^2} = \sqrt{25 – 9} = \sqrt{16} = 4 \text{ cm}$$
Bước 2: Tính diện tích: $$S = \frac{a \times b}{2} = \frac{3 \times 4}{2} = \frac{12}{2} = 6 \text{ cm}^2$$
Kết luận: Diện tích tam giác là 6 cm².
Nhận xét: Đây là bộ số Pitago nổi tiếng (3, 4, 5).
4. Diện tích tam giác vuông lớn nhất khi nào?
Bài toán: Cho cạnh huyền cố định $c$. Khi nào tam giác vuông có diện tích lớn nhất?
Trả lời: Diện tích tam giác vuông lớn nhất khi tam giác đó là tam giác vuông cân!
Chứng minh:
Cho tam giác vuông có:
- Cạnh huyền: $c$ (cố định)
- Hai cạnh góc vuông: $a$ và $b$
- Ràng buộc: $a^2 + b^2 = c^2$ (định lý Pitago)
- Diện tích: $S = \frac{1}{2}ab$
Áp dụng bất đẳng thức AM-GM:
Với hai số dương $a$ và $b$, ta có: $$ab \leq \frac{a^2 + b^2}{2}$$
Dấu “=” xảy ra khi và chỉ khi $a = b$
Từ định lý Pitago: $a^2 + b^2 = c^2$
Nên: $$ab \leq \frac{c^2}{2}$$
Do đó: $$S = \frac{1}{2}ab \leq \frac{1}{2} \times \frac{c^2}{2} = \frac{c^2}{4}$$
Vậy diện tích lớn nhất: $$\boxed{S_{max} = \frac{c^2}{4}}$$
Đạt được khi $a = b$, tức là tam giác vuông cân.
Khi đó: $a = b = \frac{c}{\sqrt{2}} = \frac{c\sqrt{2}}{2}$
Kết luận: Với cạnh huyền cho trước, tam giác vuông cân có diện tích lớn nhất.
III. CÔNG THỨC TAM GIÁC VUÔNG CÂN
1. Đặc điểm tam giác vuông cân
Định nghĩa: Tam giác vuông cân là tam giác vuông có hai cạnh góc vuông bằng nhau.
Tính chất đặc biệt:
- Hai cạnh góc vuông bằng nhau: $a = b$
- Hai góc nhọn bằng nhau: mỗi góc 45°
- Cạnh huyền liên hệ với cạnh góc vuông: $c = a\sqrt{2}$
Hình minh họa:
A
|\
a | \ a√2
|45° \
|_____\
B a C
Công thức liên hệ:
- Từ cạnh góc vuông: $c = a\sqrt{2} \approx 1.414a$
- Từ cạnh huyền: $a = \frac{c}{\sqrt{2}} = \frac{c\sqrt{2}}{2}$
2. Công thức diện tích tam giác vuông cân
📌 Khi biết cạnh góc vuông $a$:
$$\boxed{S = \frac{1}{2}a^2 = \frac{a^2}{2}}$$
Cách nhớ: “Cạnh góc vuông bình phương chia đôi”
Giải thích: Vì $a = b$ nên $S = \frac{ab}{2} = \frac{a \times a}{2} = \frac{a^2}{2}$
Ví dụ 4: Tam giác vuông cân có cạnh góc vuông 6cm. Tính diện tích?
Lời giải: $$S = \frac{a^2}{2} = \frac{6^2}{2} = \frac{36}{2} = 18 \text{ cm}^2$$
Kết luận: Diện tích tam giác vuông cân là 18 cm².
📌 Khi biết cạnh huyền $c$:
Vì $a = \frac{c}{\sqrt{2}}$, nên:
$$S = \frac{a^2}{2} = \frac{1}{2} \times \left(\frac{c}{\sqrt{2}}\right)^2 = \frac{1}{2} \times \frac{c^2}{2} = \frac{c^2}{4}$$
$$\boxed{S = \frac{c^2}{4}}$$
Cách nhớ: “Cạnh huyền bình phương chia bốn”
Ví dụ 5: Tam giác vuông cân có cạnh huyền 10cm. Tính diện tích?
Lời giải: $$S = \frac{c^2}{4} = \frac{10^2}{4} = \frac{100}{4} = 25 \text{ cm}^2$$
Kết luận: Diện tích tam giác vuông cân là 25 cm².
Kiểm tra:
- Cạnh góc vuông: $a = \frac{10}{\sqrt{2}} = 5\sqrt{2} \approx 7.07$ cm
- Diện tích: $S = \frac{(5\sqrt{2})^2}{2} = \frac{50}{2} = 25$ cm² ✓
3. Công thức chu vi tam giác vuông cân
Từ cạnh góc vuông $a$:
$$P = a + a + c = 2a + a\sqrt{2}$$
$$\boxed{P = a(2 + \sqrt{2})}$$
Với $\sqrt{2} \approx 1.414$ nên: $$P \approx a \times 3.414$$
Ví dụ 6: Tam giác vuông cân có cạnh góc vuông 5cm. Tính chu vi?
Lời giải: $$P = a(2 + \sqrt{2}) = 5(2 + 1.414) = 5 \times 3.414 = 17.07 \text{ cm}$$
Hoặc tính chính xác: $$P = 5(2 + \sqrt{2}) = 10 + 5\sqrt{2} \text{ cm}$$
Từ cạnh huyền $c$:
$$P = \frac{c}{\sqrt{2}} + \frac{c}{\sqrt{2}} + c = \frac{2c}{\sqrt{2}} + c = c\sqrt{2} + c$$
$$\boxed{P = c(\sqrt{2} + 1) = c(1 + \sqrt{2})}$$
Ví dụ 7: Tam giác vuông cân có cạnh huyền 8cm. Tính chu vi?
Lời giải: $$P = c(1 + \sqrt{2}) = 8(1 + 1.414) = 8 \times 2.414 = 19.31 \text{ cm}$$
IV. CÔNG THỨC TÍNH CẠNH TAM GIÁC VUÔNG
1. Định lý Pitago (Lớp 7)
Định lý Pitago: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
$$\boxed{c^2 = a^2 + b^2}$$
Trong đó:
- $c$: Cạnh huyền (cạnh dài nhất)
- $a$, $b$: Hai cạnh góc vuông
Nguồn gốc: Định lý mang tên nhà toán học Hy Lạp cổ đại Pythagoras (khoảng 570-495 TCN), là một trong những định lý nổi tiếng và quan trọng nhất trong toán học.
Hệ quả – Công thức tính cạnh:
📌 Tính cạnh huyền khi biết hai cạnh góc vuông:
$$\boxed{c = \sqrt{a^2 + b^2}}$$
Ví dụ 8: Tính cạnh huyền khi biết hai cạnh góc vuông là 6cm và 8cm?
Lời giải: $$c = \sqrt{a^2 + b^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ cm}$$
Kết luận: Cạnh huyền dài 10 cm.
Nhận xét: Đây là bộ số Pitago (6, 8, 10), là bội của (3, 4, 5).
📌 Tính cạnh góc vuông khi biết cạnh huyền và cạnh góc vuông còn lại:
$$\boxed{a = \sqrt{c^2 – b^2}}$$
$$\boxed{b = \sqrt{c^2 – a^2}}$$
Ví dụ 9: Tam giác vuông có cạnh huyền 13cm, một cạnh góc vuông 5cm. Tính cạnh góc vuông còn lại?
Lời giải: $$a = \sqrt{c^2 – b^2} = \sqrt{13^2 – 5^2} = \sqrt{169 – 25} = \sqrt{144} = 12 \text{ cm}$$
Kết luận: Cạnh góc vuông còn lại dài 12 cm.
Nhận xét: Đây là bộ số Pitago nổi tiếng (5, 12, 13).
2. Công thức tính cạnh trong tam giác vuông cân
Từ cạnh góc vuông $a$ tính cạnh huyền $c$:
$$\boxed{c = a\sqrt{2}}$$
Với $\sqrt{2} \approx 1.414$ nên: $$c \approx 1.414a$$
Ví dụ 10: Tam giác vuông cân có cạnh góc vuông 7cm. Tính cạnh huyền?
Lời giải: $$c = a\sqrt{2} = 7\sqrt{2} = 7 \times 1.414 \approx 9.90 \text{ cm}$$
Hoặc giữ nguyên dạng căn: $$c = 7\sqrt{2} \text{ cm}$$
Từ cạnh huyền $c$ tính cạnh góc vuông $a$:
$$\boxed{a = b = \frac{c}{\sqrt{2}} = \frac{c\sqrt{2}}{2}}$$
Ví dụ 11: Tam giác vuông cân có cạnh huyền 10cm. Tính cạnh góc vuông?
Lời giải:
Cách 1: $$a = \frac{c}{\sqrt{2}} = \frac{10}{\sqrt{2}} = \frac{10\sqrt{2}}{2} = 5\sqrt{2} \approx 7.07 \text{ cm}$$
Cách 2: Dùng Pitago
- $a = b$ nên $a^2 + a^2 = c^2$
- $2a^2 = 100$
- $a^2 = 50$
- $a = \sqrt{50} = 5\sqrt{2}$ cm ✓
3. Bộ số Pitago thường gặp (Lớp 7)
Định nghĩa: Bộ ba số Pitago là bộ ba số nguyên dương $(a, b, c)$ thỏa mãn $a^2 + b^2 = c^2$.
Các bộ số Pitago phổ biến:
| Bộ ba | Kiểm tra | Ứng dụng |
|---|---|---|
| (3, 4, 5) | $3^2 + 4^2 = 9 + 16 = 25 = 5^2$ ✓ | Phổ biến nhất |
| (5, 12, 13) | $5^2 + 12^2 = 25 + 144 = 169 = 13^2$ ✓ | Hay gặp trong bài tập |
| (8, 15, 17) | $8^2 + 15^2 = 64 + 225 = 289 = 17^2$ ✓ | Nâng cao |
| (7, 24, 25) | $7^2 + 24^2 = 49 + 576 = 625 = 25^2$ ✓ | Nâng cao |
| (9, 40, 41) | $9^2 + 40^2 = 81 + 1600 = 1681 = 41^2$ ✓ | Khó |
| (6, 8, 10) | $6^2 + 8^2 = 36 + 64 = 100 = 10^2$ ✓ | Bội của (3, 4, 5) |
| (9, 12, 15) | $9^2 + 12^2 = 81 + 144 = 225 = 15^2$ ✓ | Bội của (3, 4, 5) |
Quy tắc mở rộng: Nếu $(a, b, c)$ là bộ Pitago thì $(ka, kb, kc)$ cũng là bộ Pitago với mọi $k$ nguyên dương.
Ví dụ:
- $(3, 4, 5)$ là bộ Pitago
- $(6, 8, 10) = 2 \times (3, 4, 5)$ cũng là bộ Pitago
- $(30, 40, 50) = 10 \times (3, 4, 5)$ cũng là bộ Pitago
Cách sinh bộ Pitago: Với hai số nguyên $m > n > 0$:
- $a = m^2 – n^2$
- $b = 2mn$
- $c = m^2 + n^2$
V. CÔNG THỨC CHU VI TAM GIÁC VUÔNG
1. Công thức chu vi cơ bản (Lớp 5)
Định nghĩa: Chu vi tam giác vuông là tổng độ dài ba cạnh.
$$\boxed{P = a + b + c}$$
Trong đó:
- $a$, $b$: Hai cạnh góc vuông
- $c$: Cạnh huyền
- $P$: Chu vi (cùng đơn vị với các cạnh)
Ví dụ 12: Tam giác vuông có ba cạnh lần lượt là 3cm, 4cm, 5cm. Tính chu vi?
Lời giải: $$P = 3 + 4 + 5 = 12 \text{ cm}$$
Kết luận: Chu vi tam giác là 12 cm.
2. Chu vi khi biết hai cạnh góc vuông (Lớp 7)
Công thức: Khi biết hai cạnh góc vuông $a$ và $b$, ta tính cạnh huyền bằng Pitago rồi cộng vào:
$$\boxed{P = a + b + \sqrt{a^2 + b^2}}$$
Ví dụ 13: Tam giác vuông có hai cạnh góc vuông 6cm và 8cm. Tính chu vi?
Lời giải:
Bước 1: Tính cạnh huyền: $$c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ cm}$$
Bước 2: Tính chu vi: $$P = a + b + c = 6 + 8 + 10 = 24 \text{ cm}$$
Hoặc dùng công thức trực tiếp: $$P = 6 + 8 + \sqrt{6^2 + 8^2} = 14 + 10 = 24 \text{ cm}$$
Kết luận: Chu vi tam giác là 24 cm.
3. Chu vi tam giác vuông cân
Từ cạnh góc vuông $a$:
$$\boxed{P = 2a + a\sqrt{2} = a(2 + \sqrt{2})}$$
Với $\sqrt{2} \approx 1.414$: $$P \approx a \times 3.414$$
Ví dụ 14: Tam giác vuông cân có cạnh góc vuông 4cm. Tính chu vi?
Lời giải: $$P = a(2 + \sqrt{2}) = 4(2 + 1.414) = 4 \times 3.414 = 13.66 \text{ cm}$$
Hoặc: $$P = 4(2 + \sqrt{2}) = 8 + 4\sqrt{2} \text{ cm}$$
Từ cạnh huyền $c$:
$$\boxed{P = c + c\sqrt{2} = c(1 + \sqrt{2})}$$
Với $\sqrt{2} \approx 1.414$: $$P \approx c \times 2.414$$
Ví dụ 15: Tam giác vuông cân có cạnh huyền 12cm. Tính chu vi?
Lời giải: $$P = c(1 + \sqrt{2}) = 12(1 + 1.414) = 12 \times 2.414 = 28.97 \text{ cm}$$
VI. BẢNG CÔNG THỨC TỔNG HỢP
A. Công thức diện tích
| Trường hợp | Công thức | Lớp học | Ghi chú |
|---|---|---|---|
| Biết 2 cạnh góc vuông $a$, $b$ | $S = \frac{ab}{2}$ | Lớp 5 | Công thức cơ bản nhất |
| Biết cạnh huyền $c$ + đường cao $h$ | $S = \frac{ch}{2}$ | Lớp 8 | Dùng hệ thức lượng |
| Tam giác vuông cân (cạnh $a$) | $S = \frac{a^2}{2}$ | Lớp 7 | $a$ là cạnh góc vuông |
| Tam giác vuông cân (cạnh huyền $c$) | $S = \frac{c^2}{4}$ | Lớp 7 | Diện tích max với $c$ cố định |
B. Công thức tính cạnh (Định lý Pitago)
| Cần tìm | Biết | Công thức | Lớp học |
|---|---|---|---|
| Cạnh huyền $c$ | $a$, $b$ | $c = \sqrt{a^2 + b^2}$ | Lớp 7 |
| Cạnh góc vuông $a$ | $b$, $c$ | $a = \sqrt{c^2 – b^2}$ | Lớp 7 |
| Cạnh góc vuông $b$ | $a$, $c$ | $b = \sqrt{c^2 – a^2}$ | Lớp 7 |
Quy tắc ghi nhớ: “Bình phương cộng lại cho cạnh huyền, bình phương trừ nhau cho cạnh góc vuông”
C. Công thức tam giác vuông cân
| Đại lượng | Từ cạnh góc vuông $a$ | Từ cạnh huyền $c$ |
|---|---|---|
| Cạnh huyền | $c = a\sqrt{2}$ | – |
| Cạnh góc vuông | – | $a = \frac{c}{\sqrt{2}} = \frac{c\sqrt{2}}{2}$ |
| Diện tích | $S = \frac{a^2}{2}$ | $S = \frac{c^2}{4}$ |
| Chu vi | $P = a(2 + \sqrt{2})$ | $P = c(1 + \sqrt{2})$ |
Hằng số hữu ích: $\sqrt{2} \approx 1.414$, $2 + \sqrt{2} \approx 3.414$, $1 + \sqrt{2} \approx 2.414$
D. Công thức chu vi
| Trường hợp | Công thức | Ghi chú |
|---|---|---|
| Tam giác vuông thường | $P = a + b + c$ | Cộng 3 cạnh |
| Biết 2 cạnh góc vuông | $P = a + b + \sqrt{a^2+b^2}$ | Tính $c$ trước |
| Tam giác vuông cân (từ $a$) | $P = a(2 + \sqrt{2})$ | $a$ là cạnh góc vuông |
| Tam giác vuông cân (từ $c$) | $P = c(1 + \sqrt{2})$ | $c$ là cạnh huyền |
VII. BÀI TẬP MẪU THEO LỚP
Dạng 1: Tính diện tích (Lớp 5)
Bài 1: Một tam giác vuông có hai cạnh góc vuông lần lượt là 5cm và 12cm. Tính diện tích và chu vi của tam giác đó?
Lời giải:
Tính diện tích: $$S = \frac{a \times b}{2} = \frac{5 \times 12}{2} = \frac{60}{2} = 30 \text{ cm}^2$$
Tính chu vi:
Bước 1: Tính cạnh huyền bằng định lý Pitago: $$c = \sqrt{a^2 + b^2} = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13 \text{ cm}$$
Bước 2: Tính chu vi: $$P = a + b + c = 5 + 12 + 13 = 30 \text{ cm}$$
Kết luận:
- Diện tích: 30 cm²
- Chu vi: 30 cm
Nhận xét: Đây là bộ số Pitago (5, 12, 13).
Dạng 2: Tính cạnh bằng Pitago (Lớp 7)
Bài 2: Một tam giác vuông có cạnh huyền dài 25cm, một cạnh góc vuông dài 7cm. Hãy tính: a) Độ dài cạnh góc vuông còn lại b) Diện tích tam giác
Lời giải:
Câu a) Tính cạnh góc vuông còn lại:
Áp dụng định lý Pitago: $$b = \sqrt{c^2 – a^2} = \sqrt{25^2 – 7^2} = \sqrt{625 – 49} = \sqrt{576} = 24 \text{ cm}$$
Câu b) Tính diện tích: $$S = \frac{a \times b}{2} = \frac{7 \times 24}{2} = \frac{168}{2} = 84 \text{ cm}^2$$
Kết luận:
- Cạnh góc vuông còn lại: 24 cm
- Diện tích: 84 cm²
Nhận xét: Đây là bộ số Pitago (7, 24, 25).
Dạng 3: Tam giác vuông cân (Lớp 7)
Bài 3: Một tam giác vuông cân có cạnh góc vuông dài 8cm. Hãy tính: a) Độ dài cạnh huyền b) Diện tích c) Chu vi
Lời giải:
Câu a) Tính cạnh huyền: $$c = a\sqrt{2} = 8\sqrt{2} = 8 \times 1.414 = 11.31 \text{ cm}$$
Hoặc giữ nguyên: $c = 8\sqrt{2}$ cm
Câu b) Tính diện tích: $$S = \frac{a^2}{2} = \frac{8^2}{2} = \frac{64}{2} = 32 \text{ cm}^2$$
Câu c) Tính chu vi: $$P = a(2 + \sqrt{2}) = 8(2 + 1.414) = 8 \times 3.414 = 27.31 \text{ cm}$$
Hoặc: $P = 16 + 8\sqrt{2}$ cm
Kết luận:
- Cạnh huyền: $8\sqrt{2} \approx 11.31$ cm
- Diện tích: 32 cm²
- Chu vi: $16 + 8\sqrt{2} \approx 27.31$ cm
Bài 4: Một tam giác vuông cân có cạnh huyền dài 14cm. Tính diện tích của tam giác?
Lời giải:
Áp dụng công thức diện tích tam giác vuông cân khi biết cạnh huyền: $$S = \frac{c^2}{4} = \frac{14^2}{4} = \frac{196}{4} = 49 \text{ cm}^2$$
Kết luận: Diện tích tam giác là 49 cm².
Kiểm tra bằng cách khác:
- Cạnh góc vuông: $a = \frac{14}{\sqrt{2}} = 7\sqrt{2}$ cm
- Diện tích: $S = \frac{a^2}{2} = \frac{(7\sqrt{2})^2}{2} = \frac{98}{2} = 49$ cm² ✓
Dạng 4: Đường cao trong tam giác vuông (Lớp 8)
Bài 5: Một tam giác vuông có hai cạnh góc vuông là 6cm và 8cm. Tính độ dài đường cao ứng với cạnh huyền?
Lời giải:
Bước 1: Tính cạnh huyền: $$c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10 \text{ cm}$$
Bước 2: Tính diện tích theo hai cạnh góc vuông: $$S = \frac{a \times b}{2} = \frac{6 \times 8}{2} = 24 \text{ cm}^2$$
Bước 3: Tính đường cao $h$ từ công thức $S = \frac{c \times h}{2}$: $$24 = \frac{10 \times h}{2}$$ $$24 = 5h$$ $$h = \frac{24}{5} = 4.8 \text{ cm}$$
Kết luận: Đường cao ứng với cạnh huyền dài 4.8 cm.
Công thức tổng quát: $h = \frac{ab}{c} = \frac{ab}{\sqrt{a^2+b^2}}$
Dạng 5: Diện tích lớn nhất (Lớp 9)
Bài 6: Một tam giác vuông có cạnh huyền cố định bằng 20cm. Hỏi tam giác đó có diện tích lớn nhất bằng bao nhiêu?
Lời giải:
Theo lý thuyết đã chứng minh ở phần II.4, diện tích tam giác vuông lớn nhất khi tam giác đó là tam giác vuông cân.
Áp dụng công thức: $$S_{max} = \frac{c^2}{4} = \frac{20^2}{4} = \frac{400}{4} = 100 \text{ cm}^2$$
Kết luận: Diện tích lớn nhất của tam giác là 100 cm², đạt được khi tam giác là tam giác vuông cân với mỗi cạnh góc vuông bằng $10\sqrt{2}$ cm.
Dạng 6: Bộ số Pitago (Lớp 7)
Bài 7: Kiểm tra xem bộ ba số (9, 12, 15) có phải là độ dài ba cạnh của tam giác vuông không? Nếu đúng, hãy chỉ ra cạnh nào là cạnh huyền và tính diện tích tam giác đó.
Lời giải:
Kiểm tra điều kiện Pitago:
Cạnh dài nhất là 15, giả sử đây là cạnh huyền.
Kiểm tra: $9^2 + 12^2 = 15^2$? $$9^2 + 12^2 = 81 + 144 = 225$$ $$15^2 = 225$$
Vậy $9^2 + 12^2 = 15^2$ ✓
Kết luận 1: Bộ ba (9, 12, 15) là độ dài ba cạnh của tam giác vuông, với:
- Hai cạnh góc vuông: 9cm và 12cm
- Cạnh huyền: 15cm
Nhận xét: Đây là bội của bộ số Pitago (3, 4, 5): $(9, 12, 15) = 3 \times (3, 4, 5)$
Tính diện tích: $$S = \frac{9 \times 12}{2} = \frac{108}{2} = 54 \text{ cm}^2$$
Kết luận 2: Diện tích tam giác là 54 cm².
VIII. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Công thức diện tích:
Tam giác vuông thường:
“Nhân hai cạnh góc vuông rồi chia đôi”
$$S = \frac{ab}{2}$$
Tam giác vuông cân:
“Cạnh bình phương chia đôi”
$$S = \frac{a^2}{2} \text{ (từ cạnh góc vuông)}$$ $$S = \frac{c^2}{4} \text{ (từ cạnh huyền)}$$
Định lý Pitago:
“Bình phương cộng lại”
$$c^2 = a^2 + b^2$$
Cách nhớ khác: “Huyền bình bằng tổng hai góc bình”
Hệ quả:
- Tìm cạnh huyền: $c = \sqrt{a^2 + b^2}$ (cộng rồi lấy căn)
- Tìm cạnh góc vuông: $a = \sqrt{c^2 – b^2}$ (trừ rồi lấy căn)
Tam giác vuông cân:
“Nhân căn hai”
- Từ cạnh góc vuông → cạnh huyền: nhân $\sqrt{2}$
- Từ cạnh huyền → cạnh góc vuông: chia $\sqrt{2}$
$$c = a\sqrt{2} \quad \text{hoặc} \quad a = \frac{c}{\sqrt{2}}$$
Ghi nhớ: $\sqrt{2} \approx 1.414$ (dễ nhớ: 1-4-1-4)
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Quên chia 2 trong công thức diện tích
Sai:
- $S = ab$
Đúng:
- $S = \frac{ab}{2}$ ✓
Lưu ý: Tam giác bằng một nửa hình chữ nhật, nên nhớ chia 2.
❌ SAI LẦM 2: Nhầm cạnh huyền và cạnh góc vuông trong Pitago
Sai:
- $a^2 = b^2 + c^2$ ❌ (lấy cạnh góc vuông làm tổng)
Đúng:
- $c^2 = a^2 + b^2$ ✓ (cạnh huyền bình phương)
Cách tránh: Luôn nhớ cạnh huyền là cạnh dài nhất, đối diện góc vuông.
❌ SAI LẦM 3: Quên $\sqrt{2}$ trong tam giác vuông cân
Sai:
- $c = 2a$
Đúng:
- $c = a\sqrt{2}$ ✓
❌ SAI LẦM 4: Nhầm công thức tam giác vuông cân với tam giác vuông thường
Sai:
- Dùng $S = \frac{a^2}{2}$ cho tam giác vuông có hai cạnh góc vuông khác nhau
Đúng:
- $S = \frac{a^2}{2}$ chỉ dùng cho tam giác vuông cân (hai cạnh góc vuông bằng nhau) ✓
- Tam giác vuông thường: $S = \frac{ab}{2}$ ✓
3. Kiểm tra nhanh
Kiểm tra 1: Cạnh huyền luôn dài nhất
Trong tam giác vuông, nếu $c$ là cạnh huyền thì: $$c > a \text{ và } c > b$$
Nếu không thỏa điều kiện này → sai!
Kiểm tra 2: Tam giác vuông cân
Cạnh huyền ≈ 1.41 × cạnh góc vuông
Ví dụ: Nếu cạnh góc vuông 7cm → cạnh huyền ≈ 9.9cm
Kiểm tra 3: Bộ số Pitago phổ biến
Nhận biết ngay các bộ:
- (3, 4, 5) và bội: (6, 8, 10), (9, 12, 15), (15, 20, 25)…
- (5, 12, 13)
- (8, 15, 17)
- (7, 24, 25)
Kiểm tra 4: Công thức ngược
Sau khi tính, thử lại bằng công thức khác:
- Tính diện tích từ hai cạnh góc vuông → kiểm tra bằng cạnh huyền và đường cao
- Tính cạnh từ Pitago → kiểm tra bằng $a^2 + b^2 = c^2$
4. Quy trình giải bài tập
Bước 1: Đọc kỹ đề bài
- Xác định tam giác vuông hay tam giác vuông cân?
- Biết những đại lượng nào?
- Cần tìm đại lượng gì?
Bước 2: Vẽ hình (nếu có thể)
- Đánh dấu góc vuông
- Ghi rõ độ dài các cạnh đã biết
- Chú thích cạnh huyền
Bước 3: Chọn công thức phù hợp
- Diện tích: $S = \frac{ab}{2}$ hoặc $S = \frac{a^2}{2}$ (vuông cân)
- Tính cạnh: Định lý Pitago
- Chu vi: $P = a + b + c$
Bước 4: Tính toán cẩn thận
- Thực hiện các phép tính từng bước
- Chú ý đơn vị (cm, m, dm…)
- Kết quả diện tích có đơn vị bình phương (cm², m²…)
Bước 5: Kiểm tra kết quả
- Xem kết quả có hợp lý không?
- Cạnh huyền có dài nhất không?
- Thử lại bằng công thức khác
IX. KẾT LUẬN
Bài viết đã hệ thống hóa đầy đủ các công thức tam giác vuông từ cơ bản đến nâng cao:
Công thức diện tích:
- Tam giác vuông thường: $S = \frac{ab}{2}$ (Lớp 5)
- Tam giác vuông cân (từ cạnh $a$): $S = \frac{a^2}{2}$ (Lớp 7)
- Tam giác vuông cân (từ cạnh huyền $c$): $S = \frac{c^2}{4}$ (Lớp 7)
- Với cạnh huyền và đường cao: $S = \frac{ch}{2}$ (Lớp 8)
Định lý Pitago:
- Công thức cơ bản: $c^2 = a^2 + b^2$ (Lớp 7)
- Tính cạnh huyền: $c = \sqrt{a^2 + b^2}$
- Tính cạnh góc vuông: $a = \sqrt{c^2 – b^2}$
Công thức tam giác vuông cân:
- Liên hệ cạnh: $c = a\sqrt{2}$ hoặc $a = \frac{c}{\sqrt{2}}$
- Diện tích: $S = \frac{a^2}{2}$ hoặc $S = \frac{c^2}{4}$
- Chu vi: $P = a(2 + \sqrt{2})$ hoặc $P = c(1 + \sqrt{2})$
Công thức chu vi:
- Công thức cơ bản: $P = a + b + c$ (Lớp 5)
- Biết hai cạnh góc vuông: $P = a + b + \sqrt{a^2+b^2}$ (Lớp 7)
Bộ số Pitago phổ biến:
- (3, 4, 5), (5, 12, 13), (8, 15, 17), (7, 24, 25)
- Các bội của chúng
Công thức QUAN TRỌNG NHẤT cần nhớ
1. Diện tích tam giác vuông:
$$\boxed{S = \frac{ab}{2}}$$
2. Định lý Pitago:
$$\boxed{c = \sqrt{a^2 + b^2}}$$
3. Tam giác vuông cân:
$$\boxed{c = a\sqrt{2}}$$
Lời khuyên học tập
📌 Học thuộc ba công thức vàng: Diện tích, Pitago, tam giác vuông cân
📌 Nhớ bộ số Pitago: (3, 4, 5) là quan trọng nhất, các bộ khác là mở rộng
📌 Vẽ hình khi làm bài: Giúp hình dung rõ ràng và tránh nhầm lẫn
📌 Phân biệt tam giác vuông và tam giác vuông cân: Dùng đúng công thức
📌 Kiểm tra kết quả: Cạnh huyền luôn dài nhất, diện tích luôn dương
📌 Luyện tập nhiều dạng bài: Từ cơ bản đến nâng cao theo từng lớp

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
