Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. KHÁI NIỆM VỀ TIỆM CẬN
- 1. Tiệm cận là gì?
- 2. Phân loại tiệm cận
- 3. Ứng dụng của tiệm cận
- 4. Khi nào cần tìm tiệm cận?
- II. TIỆM CẬN ĐỨNG
- 1. Định nghĩa
- 2. Công thức tìm tiệm cận đứng
- 3. Ví dụ minh họa
- 4. Dấu hiệu nhận biết nhanh
- III. TIỆM CẬN NGANG
- 1. Định nghĩa
- 2. Công thức tìm tiệm cận ngang
- 3. Ví dụ minh họa
- 4. Lưu ý quan trọng
- IV. TIỆM CẬN XIÊN
- 1. Định nghĩa
- 2. Công thức tính tiệm cận xiên
- Phương pháp chia đa thức (nhanh hơn):
- 3. Ví dụ minh họa
- 4. Điều kiện để có tiệm cận xiên
- V. BẢNG TỔNG HỢP CÔNG THỨC
- Bảng 1: So sánh 3 loại tiệm cận
- Bảng 2: Công thức cho hàm phân thức $y = \frac{P(x)}{Q(x)}$
- Bảng 3: Công thức tính tiệm cận xiên
- Bảng 4: Các trường hợp đặc biệt thường gặp
- VI. PHƯƠNG PHÁP GIẢI TỔNG HỢP
- Quy trình tìm TẤT CẢ các tiệm cận (7 bước)
- Sơ đồ tư duy
- Ví dụ tổng hợp
- VII. MẸO VÀ LƯU Ý
- 1. Các sai lầm thường gặp
- 2. Mẹo nhận biết nhanh
- 3. Thứ tự ưu tiên khi làm bài thi
- 4. Cách kiểm tra kết quả
- VIII. KẾT LUẬN
- Những điểm cần nhớ
- So sánh 3 loại tiệm cận
- Sơ đồ tổng quát
- Câu hỏi thường gặp (FAQ)
I. KHÁI NIỆM VỀ TIỆM CẬN
1. Tiệm cận là gì?
Định nghĩa trực quan:
Tiệm cận là đường thẳng mà đồ thị hàm số tiến gần đến khi:
- Biến số $x$ tiến tới vô cực ($x \to +\infty$ hoặc $x \to -\infty$)
- Hoặc biến số $x$ tiến tới một giá trị đặc biệt $x_0$
Nói cách khác, khoảng cách từ các điểm trên đồ thị đến đường tiệm cận tiến dần về 0 nhưng đồ thị không nhất thiết chạm vào đường tiệm cận.
Ý nghĩa hình học:
- Tiệm cận cho biết “hành vi” của hàm số ở xa (khi $x \to \pm\infty$) hoặc gần một điểm đặc biệt
- Giúp vẽ đồ thị chính xác hơn, đặc biệt là phần ở xa hoặc gần các điểm kỳ dị
- Là ranh giới mà đồ thị không thể vượt qua (tiệm cận đứng) hoặc tiến gần đến (tiệm cận ngang, xiên)
- Thể hiện xu hướng biến thiên của hàm số
Ví dụ trực quan:
- Hàm $y = \frac{1}{x}$ có tiệm cận đứng $x = 0$ và tiệm cận ngang $y = 0$
- Khi $x$ càng lớn, đồ thị càng gần trục Ox nhưng không bao giờ chạm vào
2. Phân loại tiệm cận
Có 3 loại tiệm cận cơ bản trong chương trình Toán phổ thông:
| Loại | Dạng phương trình | Đặc điểm | Hướng |
|---|---|---|---|
| Tiệm cận đứng | $x = x_0$ | Đường thẳng thẳng đứng | Song song với Oy |
| Tiệm cận ngang | $y = y_0$ | Đường thẳng nằm ngang | Song song với Ox |
| Tiệm cận xiên | $y = ax + b$ $(a \neq 0)$ | Đường thẳng nghiêng | Không song song với trục tọa độ |
Lưu ý quan trọng:
✅ Một đồ thị có thể có nhiều tiệm cận đứng (mỗi điểm kỳ dị cho một tiệm cận)
✅ Một đồ thị có tối đa 2 tiệm cận ngang (một khi $x \to +\infty$, một khi $x \to -\infty$)
⚠️ Nếu có tiệm cận ngang thì KHÔNG có tiệm cận xiên và ngược lại
✅ Tiệm cận xiên xuất hiện khi bậc tử = bậc mẫu + 1 (với hàm phân thức)
✅ Một hàm số có thể có cả tiệm cận đứng VÀ tiệm cận ngang/xiên
3. Ứng dụng của tiệm cận
Trong toán học:
- Khảo sát hàm số: Xác định hành vi của hàm số ở vô cực và gần các điểm kỳ dị
- Vẽ đồ thị chính xác: Tiệm cận là “khung xương” của đồ thị, giúp định hình đường cong
- Xác định miền giá trị: Biết được hàm số có thể đạt những giá trị nào
- Nghiên cứu hàm số: Hiểu sâu về tính chất và đặc điểm của hàm số
Trong thực tế:
Kinh tế:
- Chi phí bình quân tiến đến một giá trị cố định khi sản lượng tăng lên vô hạn
- Doanh thu cận biên giảm dần khi sản xuất nhiều
Vật lý:
- Vận tốc giới hạn của vật rơi trong môi trường có ma sát
- Nhiệt độ của vật nguội dần tiến về nhiệt độ môi trường
Sinh học:
- Dân số tiến đến sức chứa tối đa (carrying capacity) của môi trường
- Nồng độ thuốc trong máu sau khi uống
Kỹ thuật:
- Phản ứng của hệ thống điều khiển khi thời gian tiến tới vô cực
- Đáp ứng tần số của mạch điện
4. Khi nào cần tìm tiệm cận?
✅ Bài toán khảo sát và vẽ đồ thị hàm số – Đây là ứng dụng quan trọng nhất
✅ Bài toán tìm giá trị lớn nhất, nhỏ nhất – Tiệm cận cho biết giới hạn của hàm số
✅ Xác định tính chất của hàm số – Tăng, giảm, bị chặn hay không
✅ Trong đề thi THPT Quốc gia – Câu hỏi về tiệm cận xuất hiện thường xuyên
✅ Phân tích đồ thị cho trước – Xác định phương trình hàm số từ đồ thị
II. TIỆM CẬN ĐỨNG
1. Định nghĩa
Đường thẳng $x = x_0$ được gọi là tiệm cận đứng của đồ thị hàm số $y = f(x)$ nếu ít nhất một trong các điều kiện sau xảy ra:
$$\lim_{x \to x_0^+} f(x) = +\infty \quad \text{hoặc} \quad \lim_{x \to x_0^+} f(x) = -\infty$$
$$\lim_{x \to x_0^-} f(x) = +\infty \quad \text{hoặc} \quad \lim_{x \to x_0^-} f(x) = -\infty$$
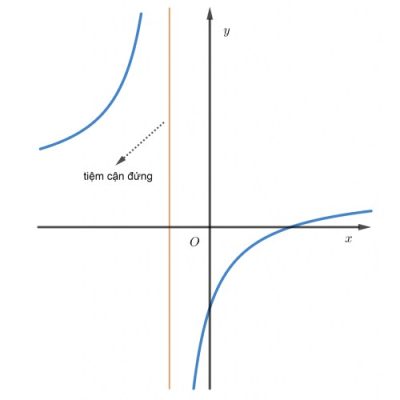
Giải thích:
- Khi $x$ tiến gần đến $x_0$ (từ bên phải hoặc bên trái), giá trị hàm số $|f(x)|$ tăng vô hạn
- Đồ thị “bay lên” hoặc “rơi xuống” theo phương thẳng đứng khi $x$ gần $x_0$
- Đường thẳng $x = x_0$ là ranh giới mà đồ thị không thể vượt qua
Ý nghĩa:
- $x_0$ thường là điểm mà hàm số không xác định (mẫu số bằng 0)
- Tiệm cận đứng chia mặt phẳng thành các miền, đồ thị nằm ở các miền khác nhau
2. Công thức tìm tiệm cận đứng
Đối với hàm phân thức $y = \frac{P(x)}{Q(x)}$:
$$\boxed{x = x_0 \text{ là TCĐ} \Leftrightarrow \begin{cases} Q(x_0) = 0 \\ P(x_0) \neq 0 \end{cases}}$$
Điều kiện:
- Mẫu số bằng 0 tại $x_0$: $Q(x_0) = 0$
- Tử số khác 0 tại $x_0$: $P(x_0) \neq 0$
Quy trình tìm tiệm cận đứng (5 bước):
Bước 1: Xác định miền xác định của hàm số (tìm điều kiện để mẫu $\neq 0$)
Bước 2: Giải phương trình $Q(x) = 0$ để tìm các nghiệm $x_1, x_2, …, x_n$
Bước 3: Với mỗi nghiệm $x_i$, kiểm tra $P(x_i) \neq 0$
Bước 4: Nếu thỏa mãn, kết luận $x = x_i$ là tiệm cận đứng
Bước 5: Liệt kê tất cả các tiệm cận đứng
Lưu ý đặc biệt:
⚠️ Nếu $P(x_0) = Q(x_0) = 0$ (cả tử và mẫu đều bằng 0):
- Phải rút gọn phân thức trước bằng cách phân tích và giản ước
- Sau khi rút gọn, kiểm tra lại điều kiện
⚠️ Hàm khác ngoài phân thức:
- Hàm logarit: $y = \ln(g(x))$ có TCĐ tại nghiệm của $g(x) = 0$ (nếu giới hạn là $-\infty$)
- Hàm mũ: Hiếm khi có TCĐ
- Hàm căn: Có thể có TCĐ tại biên của miền xác định
3. Ví dụ minh họa
Ví dụ 1 (Cơ bản – Một tiệm cận đứng):
Tìm tiệm cận đứng của hàm số $y = \frac{x+1}{x-2}$
Lời giải:
Bước 1: Miền xác định: $x \neq 2$
Bước 2: Giải phương trình mẫu = 0: $$x – 2 = 0 \Leftrightarrow x = 2$$
Bước 3: Kiểm tra tử số tại $x = 2$: $$P(2) = 2 + 1 = 3 \neq 0 \quad \text{✓}$$
Bước 4: Kết luận: Đường thẳng $\boxed{x = 2}$ là tiệm cận đứng
Kiểm tra bằng giới hạn:
- $\lim_{x \to 2^+} \frac{x+1}{x-2} = +\infty$ (vì tử dương, mẫu dương tiến về 0)
- $\lim_{x \to 2^-} \frac{x+1}{x-2} = -\infty$ (vì tử dương, mẫu âm tiến về 0)
Ví dụ 2 (Nhiều tiệm cận đứng):
Tìm tiệm cận đứng của hàm số $y = \frac{x}{x^2 – 4}$
Lời giải:
Bước 1: Miền xác định: $x^2 – 4 \neq 0 \Leftrightarrow x \neq \pm 2$
Bước 2: Giải phương trình mẫu = 0: $$x^2 – 4 = 0$$ $$(x-2)(x+2) = 0$$ $$x = 2 \text{ hoặc } x = -2$$
Bước 3: Kiểm tra tử số:
- Tại $x = 2$: $P(2) = 2 \neq 0$ ✓
- Tại $x = -2$: $P(-2) = -2 \neq 0$ ✓
Bước 4: Kết luận: Có 2 tiệm cận đứng:
- $\boxed{x = 2}$
- $\boxed{x = -2}$
Ví dụ 3 (Cần rút gọn phân thức):
Tìm tiệm cận đứng của hàm số $y = \frac{x^2 – 1}{x^2 – 3x + 2}$
Lời giải:
Bước 1: Phân tích tử và mẫu: $$y = \frac{(x-1)(x+1)}{(x-1)(x-2)}$$
Bước 2: Rút gọn (với $x \neq 1$): $$y = \frac{x+1}{x-2}$$
Bước 3: Tìm nghiệm mẫu sau rút gọn: $$x – 2 = 0 \Leftrightarrow x = 2$$
Bước 4: Kiểm tra tử số: $$P(2) = 2 + 1 = 3 \neq 0 \quad \text{✓}$$
Kết luận: Tiệm cận đứng duy nhất là $\boxed{x = 2}$
Lưu ý: Không có tiệm cận đứng tại $x = 1$ vì đã bị rút gọn (đây chỉ là điểm bị loại khỏi miền xác định, không phải tiệm cận đứng).
Ví dụ 4 (Hàm logarit):
Tìm tiệm cận đứng của hàm số $y = \ln(x – 1)$
Lời giải:
Bước 1: Điều kiện xác định: $$x – 1 > 0 \Leftrightarrow x > 1$$
Bước 2: Xét giới hạn tại biên miền xác định: $$\lim_{x \to 1^+} \ln(x-1) = -\infty$$
Kết luận: Đường thẳng $\boxed{x = 1}$ là tiệm cận đứng
Giải thích: Khi $x$ tiến về 1 từ bên phải, $(x-1)$ tiến về $0^+$, do đó $\ln(x-1) \to -\infty$.
Ví dụ 5 (Không có tiệm cận đứng):
Tìm tiệm cận đứng của hàm số $y = \frac{x^2 + 1}{x^2 + 4}$
Lời giải:
Bước 1: Giải phương trình mẫu = 0: $$x^2 + 4 = 0$$ $$x^2 = -4$$
Phương trình vô nghiệm (vì $x^2 \geq 0$ với mọi $x \in \mathbb{R}$)
Kết luận: Hàm số không có tiệm cận đứng
Giải thích: Mẫu số $x^2 + 4 \geq 4 > 0$ với mọi $x$, nên hàm số xác định trên toàn trục số và không có điểm kỳ dị.
4. Dấu hiệu nhận biết nhanh
✅ Hàm phân thức $\frac{P(x)}{Q(x)}$: Giải $Q(x) = 0$, kiểm tra $P(x_0) \neq 0$
✅ Hàm $\ln(g(x))$: Tìm nghiệm $g(x) = 0$ (nếu giới hạn là $-\infty$)
✅ Hàm $\frac{1}{g(x)}$: Tìm nghiệm $g(x) = 0$
✅ Hàm $\tan x$: TCĐ tại $x = \frac{\pi}{2} + k\pi$
✅ Hàm $\cot x$: TCĐ tại $x = k\pi$
III. TIỆM CẬN NGANG
1. Định nghĩa
Đường thẳng $y = y_0$ được gọi là tiệm cận ngang của đồ thị hàm số $y = f(x)$ nếu ít nhất một trong hai điều kiện sau xảy ra:
$$\lim_{x \to +\infty} f(x) = y_0$$
$$\lim_{x \to -\infty} f(x) = y_0$$
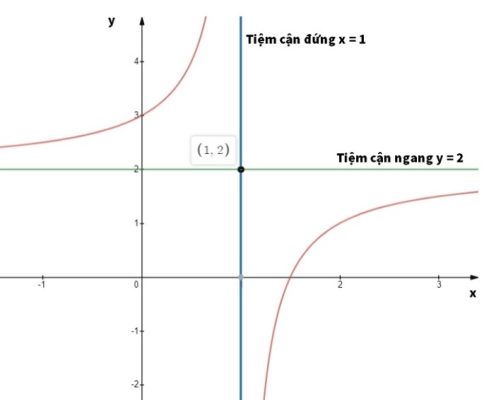
Giải thích:
- Khi $x$ tiến ra vô cực (dương hoặc âm), giá trị hàm số tiến gần đến một giá trị cố định $y_0$
- Đồ thị tiến gần đến đường thẳng $y = y_0$ khi càng ra xa
- Hàm số có giá trị “ổn định” ở vô cực
Ý nghĩa:
- Tiệm cận ngang cho biết giới hạn của hàm số khi $x$ rất lớn hoặc rất nhỏ
- Trong thực tế, đây thường là giá trị cân bằng, giá trị bão hòa
2. Công thức tìm tiệm cận ngang
Đối với hàm phân thức $y = \frac{a_nx^n + a_{n-1}x^{n-1} + … + a_0}{b_mx^m + b_{m-1}x^{m-1} + … + b_0}$:
| Trường hợp | Tiệm cận ngang | Giải thích |
|---|---|---|
| Bậc tử < Bậc mẫu $(n < m)$ | $y = 0$ | Mẫu tăng nhanh hơn tử, phân số tiến về 0 |
| Bậc tử = Bậc mẫu $(n = m)$ | $y = \frac{a_n}{b_m}$ | Tỉ số hệ số bậc cao nhất |
| Bậc tử > Bậc mẫu $(n > m)$ | Không có TCN | Tử tăng nhanh hơn, hàm tiến về vô cực |
Quy trình tìm tiệm cận ngang:
Bước 1: Xác định bậc của tử số ($n$) và mẫu số ($m$)
Bước 2: So sánh $n$ và $m$:
- Nếu $n < m$ → TCN: $y = 0$
- Nếu $n = m$ → TCN: $y = \frac{a_n}{b_m}$ (tỉ số hệ số bậc cao nhất)
- Nếu $n > m$ → Không có TCN (có thể có TCX)
Bước 3: Kết luận tiệm cận ngang
Lưu ý:
- Nếu giới hạn khi $x \to +\infty$ khác giới hạn khi $x \to -\infty$, có thể có 2 TCN khác nhau
- Phải tính cả hai giới hạn để chắc chắn
3. Ví dụ minh họa
Ví dụ 1 (Bậc tử < Bậc mẫu):
Tìm tiệm cận ngang của hàm số $y = \frac{2x + 1}{x^2 + 3}$
Lời giải:
Bước 1: Xác định bậc:
- Bậc tử số: $n = 1$
- Bậc mẫu số: $m = 2$
Bước 2: So sánh: $n = 1 < m = 2$
Bước 3: Áp dụng công thức: $$\text{Bậc tử < Bậc mẫu} \Rightarrow \text{TCN: } y = 0$$
Kiểm tra bằng giới hạn: $$\lim_{x \to \pm\infty} \frac{2x + 1}{x^2 + 3} = \lim_{x \to \pm\infty} \frac{x(2 + \frac{1}{x})}{x^2(1 + \frac{3}{x^2})} = \lim_{x \to \pm\infty} \frac{2 + \frac{1}{x}}{x(1 + \frac{3}{x^2})} = 0$$
Kết luận: Tiệm cận ngang là $\boxed{y = 0}$ (trục hoành)
Ví dụ 2 (Bậc tử = Bậc mẫu):
Tìm tiệm cận ngang của hàm số $y = \frac{3x^2 – 2x + 1}{2x^2 + 5}$
Lời giải:
Bước 1: Xác định bậc:
- Bậc tử số: $n = 2$
- Bậc mẫu số: $m = 2$
Bước 2: So sánh: $n = m = 2$ (bằng nhau)
Bước 3: Áp dụng công thức: $$y = \frac{a_n}{b_m} = \frac{3}{2}$$
Kiểm tra bằng giới hạn: $$\lim_{x \to \pm\infty} \frac{3x^2 – 2x + 1}{2x^2 + 5} = \lim_{x \to \pm\infty} \frac{x^2(3 – \frac{2}{x} + \frac{1}{x^2})}{x^2(2 + \frac{5}{x^2})} = \frac{3}{2}$$
Kết luận: Tiệm cận ngang là $\boxed{y = \frac{3}{2}}$
Ví dụ 3 (Không có tiệm cận ngang):
Tìm tiệm cận ngang của hàm số $y = \frac{x^3 + 1}{x^2 – 1}$
Lời giải:
Bước 1: Xác định bậc:
- Bậc tử số: $n = 3$
- Bậc mẫu số: $m = 2$
Bước 2: So sánh: $n = 3 > m = 2$
Bước 3: Kết luận: Không có tiệm cận ngang
Giải thích: $$\lim_{x \to \pm\infty} \frac{x^3 + 1}{x^2 – 1} = \lim_{x \to \pm\infty} \frac{x^3}{x^2} = \lim_{x \to \pm\infty} x = \pm\infty$$
Hàm số này có tiệm cận xiên (sẽ xét ở phần sau).
Ví dụ 4 (Hàm mũ – Hai tiệm cận ngang khác nhau):
Tìm tiệm cận ngang của hàm số $y = \frac{e^x}{1 + e^x}$
Lời giải:
Bước 1: Tính giới hạn khi $x \to +\infty$: $$\lim_{x \to +\infty} \frac{e^x}{1 + e^x} = \lim_{x \to +\infty} \frac{e^x}{e^x(\frac{1}{e^x} + 1)} = \lim_{x \to +\infty} \frac{1}{\frac{1}{e^x} + 1} = \frac{1}{0 + 1} = 1$$
Bước 2: Tính giới hạn khi $x \to -\infty$: $$\lim_{x \to -\infty} \frac{e^x}{1 + e^x} = \frac{0}{1 + 0} = 0$$ (vì $e^x \to 0$ khi $x \to -\infty$)
Kết luận: Có 2 tiệm cận ngang:
- $\boxed{y = 1}$ (khi $x \to +\infty$)
- $\boxed{y = 0}$ (khi $x \to -\infty$)
Ví dụ 5 (Hàm chứa căn):
Tìm tiệm cận ngang của hàm số $y = \frac{\sqrt{4x^2 + 1}}{x + 2}$
Lời giải:
Với $x \to +\infty$: $$y = \frac{\sqrt{4x^2 + 1}}{x + 2} = \frac{\sqrt{x^2(4 + \frac{1}{x^2})}}{x(1 + \frac{2}{x})} = \frac{|x|\sqrt{4 + \frac{1}{x^2}}}{x(1 + \frac{2}{x})}$$
Vì $x > 0$ nên $|x| = x$: $$= \frac{x\sqrt{4 + \frac{1}{x^2}}}{x(1 + \frac{2}{x})} = \frac{\sqrt{4 + \frac{1}{x^2}}}{1 + \frac{2}{x}} \to \frac{\sqrt{4}}{1} = \frac{2}{1} = 2$$
Với $x \to -\infty$: Vì $x < 0$ nên $|x| = -x$: $$y = \frac{-x\sqrt{4 + \frac{1}{x^2}}}{x(1 + \frac{2}{x})} = \frac{-\sqrt{4 + \frac{1}{x^2}}}{1 + \frac{2}{x}} \to \frac{-2}{1} = -2$$
Kết luận: Có 2 tiệm cận ngang:
- $\boxed{y = 2}$ (khi $x \to +\infty$)
- $\boxed{y = -2}$ (khi $x \to -\infty$)
4. Lưu ý quan trọng
⚠️ Một hàm số có thể có 2 tiệm cận ngang khác nhau khi $x \to +\infty$ và $x \to -\infty$
⚠️ Nếu có tiệm cận ngang thì KHÔNG có tiệm cận xiên và ngược lại
✅ Với hàm phân thức, chỉ cần so sánh bậc là xong, không cần tính giới hạn
IV. TIỆM CẬN XIÊN
1. Định nghĩa
Đường thẳng $y = ax + b$ (với $a \neq 0$) được gọi là tiệm cận xiên của đồ thị hàm số $y = f(x)$ nếu:
$$\lim_{x \to +\infty} [f(x) – (ax + b)] = 0$$
hoặc
$$\lim_{x \to -\infty} [f(x) – (ax + b)] = 0$$
Giải thích:
- Khi $x$ tiến ra vô cực, khoảng cách từ đồ thị đến đường thẳng $y = ax + b$ tiến về 0
- Đồ thị “bám sát” vào đường thẳng nghiêng khi càng ra xa
- Tiệm cận xiên là “xu hướng tuyến tính” của hàm số ở vô cực
Ý nghĩa:
- Tiệm cận xiên xuất hiện khi hàm số tăng/giảm theo xu hướng tuyến tính ở vô cực
- Khác với TCN (nằm ngang), TCX có độ dốc $a \neq 0$
2. Công thức tính tiệm cận xiên
Công thức tổng quát (quan trọng nhất):
$$\boxed{\begin{cases} a = \lim_{x \to \pm\infty} \frac{f(x)}{x} \\[10pt] b = \lim_{x \to \pm\infty} [f(x) – ax] \end{cases}}$$
Điều kiện tồn tại:
- Hệ số góc $a$ phải hữu hạn và $a \neq 0$
- Tung độ gốc $b$ phải hữu hạn
- Nếu $a = 0$ → Đó là tiệm cận ngang, không phải tiệm cận xiên
Đối với hàm phân thức $y = \frac{P(x)}{Q(x)}$ với bậc $P$ = bậc $Q$ + 1:
Phương pháp chia đa thức (nhanh hơn):
Bước 1: Thực hiện phép chia đa thức $P(x) : Q(x)$
Bước 2: Viết dưới dạng: $$f(x) = ax + b + \frac{R(x)}{Q(x)}$$
Trong đó $R(x)$ là dư, có bậc < bậc $Q(x)$
Bước 3: Khi $x \to \pm\infty$: $\frac{R(x)}{Q(x)} \to 0$
Bước 4: Kết luận tiệm cận xiên: $y = ax + b$
3. Ví dụ minh họa
Ví dụ 1 (Phương pháp công thức):
Tìm tiệm cận xiên của hàm số $y = \frac{x^2 + x + 1}{x + 1}$
Lời giải:
Phương pháp 1: Dùng công thức
Bước 1: Tính hệ số góc $a$: $$a = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{x^2 + x + 1}{x(x+1)}$$ $$= \lim_{x \to +\infty} \frac{x^2 + x + 1}{x^2 + x} = \lim_{x \to +\infty} \frac{x^2(1 + \frac{1}{x} + \frac{1}{x^2})}{x^2(1 + \frac{1}{x})} = 1$$
Bước 2: Tính tung độ gốc $b$: $$b = \lim_{x \to +\infty} \left[\frac{x^2 + x + 1}{x + 1} – x\right]$$ $$= \lim_{x \to +\infty} \frac{x^2 + x + 1 – x(x+1)}{x + 1}$$ $$= \lim_{x \to +\infty} \frac{x^2 + x + 1 – x^2 – x}{x + 1}$$ $$= \lim_{x \to +\infty} \frac{1}{x + 1} = 0$$
Kết luận: Tiệm cận xiên là $\boxed{y = x}$
Ví dụ 2 (Phương pháp chia đa thức – Nhanh hơn):
Tìm tiệm cận xiên của hàm số $y = \frac{2x^2 – 3x + 1}{x – 2}$
Lời giải:
Bước 1: Thực hiện phép chia đa thức:
2x² - 3x + 1 | x - 2
-2x² + 4x | 2x + 1
____________
x + 1
-x + 2
__________
3 (dư)
Bước 2: Viết lại hàm số: $$y = 2x + 1 + \frac{3}{x – 2}$$
Bước 3: Khi $x \to \pm\infty$: $$\frac{3}{x – 2} \to 0$$
Kết luận: Tiệm cận xiên là $\boxed{y = 2x + 1}$
Giải thích: Phần $\frac{3}{x-2}$ tiến về 0 khi $x$ càng lớn, nên đồ thị càng gần đường thẳng $y = 2x + 1$.
Ví dụ 3 (Hàm có cả TCĐ và TCX):
Tìm tất cả các tiệm cận của hàm số $y = \frac{x^2 + 1}{x – 1}$
Lời giải:
Phần 1: Tìm tiệm cận đứng
- Mẫu số: $x – 1 = 0 \Leftrightarrow x = 1$
- Tử số tại $x = 1$: $1 + 1 = 2 \neq 0$ ✓
- Tiệm cận đứng: $\boxed{x = 1}$
Phần 2: Tìm tiệm cận xiên
Kiểm tra: Bậc tử = 2, Bậc mẫu = 1 → Bậc tử = Bậc mẫu + 1 ✓ (có thể có TCX)
Chia đa thức:
x² + 1 | x - 1
-x² + x | x + 1
________
x + 1
-x + 1
_______
2 (dư)
Viết lại: $y = x + 1 + \frac{2}{x – 1}$
Tiệm cận xiên: $\boxed{y = x + 1}$
Kết luận tổng hợp:
- Tiệm cận đứng: $x = 1$
- Tiệm cận xiên: $y = x + 1$
- Không có tiệm cận ngang
Ví dụ 4 (Hàm vô tỉ):
Tìm tiệm cận xiên của hàm số $y = \sqrt{x^2 + x}$
Lời giải:
Với $x \to +\infty$:
Bước 1: Tính $a$: $$a = \lim_{x \to +\infty} \frac{\sqrt{x^2 + x}}{x} = \lim_{x \to +\infty} \frac{\sqrt{x^2(1 + \frac{1}{x})}}{x}$$ $$= \lim_{x \to +\infty} \frac{|x|\sqrt{1 + \frac{1}{x}}}{x} = \lim_{x \to +\infty} \frac{x\sqrt{1 + \frac{1}{x}}}{x}$$ (vì $x > 0$ nên $|x| = x$) $$= \lim_{x \to +\infty} \sqrt{1 + \frac{1}{x}} = 1$$
Bước 2: Tính $b$: $$b = \lim_{x \to +\infty} [\sqrt{x^2 + x} – x]$$ $$= \lim_{x \to +\infty} \frac{(\sqrt{x^2 + x} – x)(\sqrt{x^2 + x} + x)}{\sqrt{x^2 + x} + x}$$ $$= \lim_{x \to +\infty} \frac{x^2 + x – x^2}{\sqrt{x^2 + x} + x}$$ $$= \lim_{x \to +\infty} \frac{x}{\sqrt{x^2 + x} + x}$$ $$= \lim_{x \to +\infty} \frac{x}{x(\sqrt{1 + \frac{1}{x}} + 1)}$$ $$= \lim_{x \to +\infty} \frac{1}{\sqrt{1 + \frac{1}{x}} + 1} = \frac{1}{1 + 1} = \frac{1}{2}$$
Kết luận: Tiệm cận xiên là $\boxed{y = x + \frac{1}{2}}$ (khi $x \to +\infty$)
Với $x \to -\infty$: Tính tương tự (hoặc không xét nếu hàm không xác định).
Ví dụ 5 (Không có tiệm cận xiên):
Kiểm tra xem hàm số $y = \frac{x^3 + 1}{x^2 + 1}$ có tiệm cận xiên không?
Lời giải:
Bước 1: Kiểm tra điều kiện:
- Bậc tử = 3, Bậc mẫu = 2
- Bậc tử = Bậc mẫu + 1 ✓ (thỏa điều kiện có thể có TCX)
Bước 2: Tính $a$: $$a = \lim_{x \to \infty} \frac{x^3 + 1}{x(x^2 + 1)} = \lim_{x \to \infty} \frac{x^3 + 1}{x^3 + x}$$ $$= \lim_{x \to \infty} \frac{x^3(1 + \frac{1}{x^3})}{x^3(1 + \frac{1}{x^2})} = 1$$
Bước 3: Tính $b$: $$b = \lim_{x \to \infty} \left[\frac{x^3 + 1}{x^2 + 1} – x\right]$$ $$= \lim_{x \to \infty} \frac{x^3 + 1 – x(x^2 + 1)}{x^2 + 1}$$ $$= \lim_{x \to \infty} \frac{x^3 + 1 – x^3 – x}{x^2 + 1}$$ $$= \lim_{x \to \infty} \frac{1 – x}{x^2 + 1} = 0$$
Kết luận: Tiệm cận xiên là $\boxed{y = x}$
4. Điều kiện để có tiệm cận xiên
✅ Hàm phân thức: Bậc tử = Bậc mẫu + 1
✅ Hàm vô tỉ: Một số hàm chứa căn có TCX
✅ Điều kiện chung: $a = \lim_{x \to \pm\infty} \frac{f(x)}{x}$ phải hữu hạn và $\neq 0$
❌ KHÔNG có TCX nếu:
- Đã có tiệm cận ngang (TCN và TCX loại trừ nhau)
- Bậc tử $\neq$ Bậc mẫu + 1 (với hàm phân thức)
- Giới hạn $a$ hoặc $b$ không hữu hạn
Quy tắc vàng: TCN và TCX KHÔNG thể cùng tồn tại!
V. BẢNG TỔNG HỢP CÔNG THỨC
Bảng 1: So sánh 3 loại tiệm cận
| Loại | Phương trình | Điều kiện | Cách tìm nhanh |
|---|---|---|---|
| Tiệm cận đứng (TCĐ) | $x = x_0$ | $\lim_{x \to x_0} |f(x)| = +\infty$ | Giải $Q(x) = 0$, kiểm tra $P(x_0) \neq 0$ |
| Tiệm cận ngang (TCN) | $y = y_0$ | $\lim_{x \to \pm\infty} f(x) = y_0$ | So sánh bậc tử/mẫu |
| Tiệm cận xiên (TCX) | $y = ax + b$ $(a \neq 0)$ | $\lim_{x \to \pm\infty} [f(x) – (ax+b)] = 0$ | Chia đa thức hoặc tính $a, b$ |
Bảng 2: Công thức cho hàm phân thức $y = \frac{P(x)}{Q(x)}$
| So sánh bậc | TCĐ | TCN | TCX |
|---|---|---|---|
| Bậc $P$ < Bậc $Q$ | $Q(x_0) = 0$<br>$P(x_0) \neq 0$ | $y = 0$ | Không có |
| Bậc $P$ = Bậc $Q$ | $Q(x_0) = 0$<br>$P(x_0) \neq 0$ | $y = \frac{a_n}{b_m}$ | Không có |
| Bậc $P$ = Bậc $Q$ + 1 | $Q(x_0) = 0$<br>$P(x_0) \neq 0$ | Không có | $y = ax + b$<br>(chia đa thức) |
| Bậc $P$ > Bậc $Q$ + 1 | $Q(x_0) = 0$<br>$P(x_0) \neq 0$ | Không có | Không có |
Ghi nhớ:
- Bậc tử < Bậc mẫu → TCN: $y = 0$
- Bậc tử = Bậc mẫu → TCN: $y = \frac{a_n}{b_m}$
- Bậc tử = Bậc mẫu + 1 → TCX (chia đa thức)
Bảng 3: Công thức tính tiệm cận xiên
| Phương pháp | Công thức | Ưu điểm | Khi nào dùng |
|---|---|---|---|
| PP1: Công thức giới hạn | $a = \lim_{x \to \pm\infty} \frac{f(x)}{x}$
$b = \lim_{x \to \pm\infty} [f(x) – ax]$ |
Áp dụng cho mọi hàm | Hàm vô tỉ, phức tạp |
| PP2: Chia đa thức | $f(x) = ax + b + \frac{R(x)}{Q(x)}$
TCX: $y = ax + b$ |
Nhanh, đơn giản | Hàm phân thức hữu tỉ |
Bảng 4: Các trường hợp đặc biệt thường gặp
| Hàm số | Tiệm cận đứng | Tiệm cận ngang | Tiệm cận xiên |
|---|---|---|---|
| $y = \frac{k}{x}$ | $x = 0$ | $y = 0$ | Không có |
| $y = \frac{ax + b}{cx + d}$ | $x = -\frac{d}{c}$ | $y = \frac{a}{c}$ | Không có |
| $y = \frac{ax^2 + bx + c}{dx + e}$ | $x = -\frac{e}{d}$ | Không có | $y = mx + n$ |
| $y = \ln x$ | $x = 0$ | Không có | Không có |
| $y = e^x$ | Không có | $y = 0$ ($x \to -\infty$) | Không có |
| $y = \arctan x$ | Không có | $y = \pm\frac{\pi}{2}$ | Không có |
| $y = \frac{1}{x^2}$ | $x = 0$ | $y = 0$ | Không có |
VI. PHƯƠNG PHÁP GIẢI TỔNG HỢP
Quy trình tìm TẤT CẢ các tiệm cận (7 bước)
Bước 1: Xác định miền xác định
- Tìm điều kiện để hàm số xác định
- Ghi rõ các giá trị $x$ bị loại
Bước 2: Tìm tiệm cận đứng
- Giải phương trình mẫu = 0 (hoặc điều kiện không xác định)
- Kiểm tra tử số $\neq$ 0 tại các điểm đó
- Nếu tử = mẫu = 0 → Rút gọn trước
Bước 3: So sánh bậc (với hàm phân thức)
- Xác định bậc tử số và bậc mẫu số
- Áp dụng quy tắc trong bảng tổng hợp
Bước 4: Tìm tiệm cận ngang (nếu có)
- Bậc tử < Bậc mẫu → TCN: $y = 0$
- Bậc tử = Bậc mẫu → TCN: $y = \frac{a_n}{b_m}$
Bước 5: Tìm tiệm cận xiên (nếu không có TCN)
- Bậc tử = Bậc mẫu + 1 → Có TCX
- Dùng phép chia đa thức hoặc tính $a, b$
Bước 6: Kiểm tra lại kết quả
- Thế vào công thức kiểm tra
- Tính giới hạn để xác nhận
Bước 7: Kết luận
- Liệt kê đầy đủ tất cả các tiệm cận tìm được
Sơ đồ tư duy
Cho hàm y = f(x)
|
↓
┌──────────────────────┴──────────────────────┐
| |
Tìm TCĐ: x = x₀ So sánh bậc tử/mẫu
(mẫu = 0, tử ≠ 0) |
┌────────────────┼────────────────┐
| | |
Bậc tử < Bậc mẫu Bậc tử = Bậc mẫu Bậc tử = Bậc mẫu + 1
| | |
TCN: y = 0 TCN: y = aₙ/bₘ TCX: y = ax + b
(chia đa thức)
Ví dụ tổng hợp
Đề bài: Tìm tất cả các tiệm cận của đồ thị hàm số $y = \frac{2x^2 – 3x + 1}{x^2 – 4}$
Lời giải đầy đủ:
Bước 1: Miền xác định $$x^2 – 4 \neq 0 \Leftrightarrow x \neq \pm 2$$
Bước 2: Tìm tiệm cận đứng
Giải phương trình mẫu = 0: $$x^2 – 4 = 0$$ $$(x-2)(x+2) = 0$$ $$x = 2 \text{ hoặc } x = -2$$
Kiểm tra tử số:
- Tại $x = 2$: $P(2) = 2(4) – 3(2) + 1 = 8 – 6 + 1 = 3 \neq 0$ ✓
- Tại $x = -2$: $P(-2) = 2(4) – 3(-2) + 1 = 8 + 6 + 1 = 15 \neq 0$ ✓
Tiệm cận đứng: $\boxed{x = 2}$ và $\boxed{x = -2}$
Bước 3: So sánh bậc
- Bậc tử số: 2
- Bậc mẫu số: 2
- Bậc tử = Bậc mẫu → Có tiệm cận ngang
Bước 4: Tìm tiệm cận ngang $$y = \frac{2x^2 + …}{x^2 + …} \to \frac{2}{1} = 2$$
Tiệm cận ngang: $\boxed{y = 2}$
Bước 5: Kiểm tra tiệm cận xiên Vì đã có TCN nên không có TCX
Kết luận tổng hợp:
- 2 tiệm cận đứng: $x = 2$ và $x = -2$
- 1 tiệm cận ngang: $y = 2$
- Không có tiệm cận xiên
VII. MẸO VÀ LƯU Ý
1. Các sai lầm thường gặp
❌ Sai lầm 1: Quên kiểm tra tử số khi tìm TCĐ
Sai:
- Chỉ giải mẫu = 0 mà không kiểm tra tử
Đúng:
- Phải có: Mẫu = 0 VÀ Tử $\neq$ 0
Ví dụ: $y = \frac{x-1}{(x-1)(x-2)}$ không có TCĐ tại $x = 1$ (vì tử cũng = 0).
❌ Sai lầm 2: Nhầm lẫn TCN và TCX
Nhớ: TCN và TCX loại trừ lẫn nhau!
- Có TCN thì KHÔNG có TCX
- Có TCX thì KHÔNG có TCN
❌ Sai lầm 3: Quên rút gọn phân thức
Nếu tử và mẫu có nhân tử chung $(x – a)$:
- Phải rút gọn trước khi tìm tiệm cận
- Điểm $x = a$ không phải là TCĐ
Ví dụ: $y = \frac{(x-1)(x+2)}{(x-1)(x-3)}$ sau rút gọn là $y = \frac{x+2}{x-3}$ → Chỉ có TCĐ tại $x = 3$
❌ Sai lầm 4: Sai khi chia đa thức
Phải thực hiện phép chia chính xác:
- Sắp xếp theo thứ tự giảm dần của bậc
- Chia từng bước cẩn thận
- Kiểm tra lại bằng phép nhân ngược
❌ Sai lầm 5: Không xét cả hai giới hạn
Một hàm có thể có:
- 2 TCN khác nhau khi $x \to +\infty$ và $x \to -\infty$
- 2 TCX khác nhau (hiếm gặp)
Ví dụ: $y = \frac{e^x}{1 + e^x}$ có TCN: $y = 1$ (khi $x \to +\infty$) và $y = 0$ (khi $x \to -\infty$)
2. Mẹo nhận biết nhanh
✅ Mẹo 1: Nhận dạng nhanh loại tiệm cận từ công thức
Nhìn vào hàm phân thức:
- Đếm bậc tử và mẫu → Biết ngay loại tiệm cận
- Mẫu = 0 → Có TCĐ
- Bậc tử ≤ Bậc mẫu → Có TCN
- Bậc tử = Bậc mẫu + 1 → Có TCX
✅ Mẹo 2: Công thức nhanh cho $y = \frac{ax + b}{cx + d}$
Không cần tính gì cả, nhớ luôn:
- TCĐ: $x = -\frac{d}{c}$ (cho mẫu = 0)
- TCN: $y = \frac{a}{c}$ (tỉ số hệ số bậc nhất)
Ví dụ: $y = \frac{2x + 3}{3x – 6}$
- TCĐ: $x = 2$
- TCN: $y = \frac{2}{3}$
✅ Mẹo 3: Kiểm tra nhanh TCX bằng chia đa thức
Chỉ cần chia đa thức, lấy phần nguyên (bỏ phần dư)
✅ Mẹo 4: Hàm đặc biệt – Nhớ luôn
| Hàm | TCĐ | TCN |
|---|---|---|
| $y = \frac{k}{x}$ | $x = 0$ | $y = 0$ |
| $y = \ln x$ | $x = 0$ | Không |
| $y = e^x$ | Không | $y = 0$ (khi $x \to -\infty$) |
3. Thứ tự ưu tiên khi làm bài thi
📝 Tìm TCĐ trước (dễ nhất, ít sai sót, 1-2 phút)
📝 Tìm TCN tiếp theo (so sánh bậc rất nhanh, 30 giây)
📝 Tìm TCX cuối cùng (phức tạp nhất, mất nhiều thời gian, 2-3 phút)
Lý do:
- TCĐ và TCN dễ, làm trước để đảm bảo điểm
- TCX khó, để sau, nếu hết thời gian thì bỏ qua
4. Cách kiểm tra kết quả
✔️ Kiểm tra TCĐ:
Thế $x = x_0$ vào:
- Mẫu → phải bằng 0
- Tử → phải khác 0
✔️ Kiểm tra TCN:
Tính lại giới hạn: $$\lim_{x \to \pm\infty} f(x) = y_0$$
✔️ Kiểm tra TCX:
Tính giới hạn: $$\lim_{x \to \pm\infty} [f(x) – (ax + b)] = 0$$
Nếu bằng 0 → Đúng ✓
VIII. KẾT LUẬN
Bài viết đã trình bày đầy đủ và chi tiết về 3 loại tiệm cận:
Tiệm cận đứng (TCĐ): $$x = x_0 \quad \text{(mẫu = 0, tử ≠ 0)}$$
Tiệm cận ngang (TCN): $$y = y_0 \quad \text{(so sánh bậc tử/mẫu)}$$
Tiệm cận xiên (TCX): $$y = ax + b \quad \text{(chia đa thức hoặc tính } a, b\text{)}$$
4 bảng công thức tổng hợp đầy đủ để tra cứu nhanh
15+ ví dụ chi tiết từ cơ bản đến nâng cao, bao quát mọi dạng bài
Quy trình 7 bước tìm tất cả tiệm cận một cách hệ thống
Mẹo nhận biết nhanh và cách tránh 5 sai lầm thường gặp
Phương pháp kiểm tra kết quả chính xác
Những điểm cần nhớ
TCĐ: Song song với trục Oy – Đường thẳng đứng $x = x_0$
TCN: Song song với trục Ox – Đường thẳng ngang $y = y_0$
TCX: Đường thẳng nghiêng $y = ax + b$ với $a \neq 0$
Quy tắc vàng: Có TCN thì KHÔNG có TCX và ngược lại
Một hàm số có thể có:
- Nhiều TCĐ (mỗi điểm kỳ dị một TCĐ)
- Tối đa 2 TCN (một khi $x \to +\infty$, một khi $x \to -\infty$)
- Tối đa 2 TCX (tương tự TCN)
Với hàm phân thức: Chỉ cần so sánh bậc là biết ngay loại tiệm cận
So sánh 3 loại tiệm cận
| Tiêu chí | TCĐ | TCN | TCX |
|---|---|---|---|
| Hình dạng | Thẳng đứng | Nằm ngang | Nghiêng |
| Phương trình | $x = x_0$ | $y = y_0$ | $y = ax + b$ |
| Điều kiện | Hàm không xác định tại $x_0$ | Giới hạn hữu hạn tại $\pm\infty$ | Bậc tử = Bậc mẫu + 1 |
| Số lượng | Có thể nhiều | Tối đa 2 | Tối đa 2 |
| Độ khó | Dễ | Dễ | Trung bình |
| Thời gian | Nhanh (1-2 phút) | Rất nhanh (30 giây) | Lâu (2-3 phút) |
| Cách tìm | Giải mẫu = 0 | So sánh bậc | Chia đa thức |
Sơ đồ tổng quát
TIỆM CẬN
|
┌───────────────┼───────────────┐
| | |
TIỆM CẬN ĐỨNG TIỆM CẬN NGANG TIỆM CẬN XIÊN
| | |
x = x₀ y = y₀ y = ax + b
| | |
Song song Oy Song song Ox Đường xiên
| | |
Mẫu = 0 So sánh bậc Chia đa thức
Tử ≠ 0 | |
| |
Bậc tử < Bậc mẫu Bậc tử = Bậc mẫu + 1
↓ ↓
y = 0 y = ax + b
Bậc tử = Bậc mẫu
↓
y = aₙ/bₘ
📚 Xem thêm các bài viết liên quan:
- [Khảo sát hàm số – Quy trình 7 bước chuẩn]
- [Công thức đạo hàm đầy đủ từ cơ bản đến nâng cao]
- [Giới hạn hàm số – Công thức và phương pháp]
- [Bài tập tiệm cận có lời giải chi tiết – 50 bài]
- [Vẽ đồ thị hàm số – Kỹ thuật và mẹo hay]
Câu hỏi thường gặp (FAQ)
Q1: Làm sao biết hàm số có tiệm cận ngang hay tiệm cận xiên?
A: Với hàm phân thức, so sánh bậc:
- Bậc tử ≤ Bậc mẫu → Có TCN
- Bậc tử = Bậc mẫu + 1 → Có TCX
- Nhớ: TCN và TCX không thể cùng tồn tại!
Q2: Khi nào cần rút gọn phân thức trước khi tìm tiệm cận?
A: Khi cả tử và mẫu đều có nhân tử chung. Ví dụ: $\frac{(x-1)(x+2)}{(x-1)(x+3)}$ cần rút gọn thành $\frac{x+2}{x+3}$ trước khi tìm tiệm cận.
Q3: Một hàm số có thể có bao nhiêu tiệm cận đứng?
A: Có thể có nhiều tiệm cận đứng, mỗi nghiệm của mẫu số (thỏa mãn tử ≠ 0) cho một tiệm cận đứng.
Q4: Tại sao có TCN thì không có TCX?
A: Vì:
- TCN: $\lim_{x \to \infty} f(x) = y_0$ (hàm tiến đến hằng số)
- TCX: $\lim_{x \to \infty} [f(x) – ax] = b$ (hàm tiến đến đường thẳng nghiêng)
Hai điều kiện này mâu thuẫn với nhau.
Q5: Làm thế nào để kiểm tra kết quả nhanh?
A:
- TCĐ: Thế $x_0$ vào mẫu phải được 0, vào tử phải khác 0
- TCN: Tính $\lim_{x \to \pm\infty} f(x)$ phải bằng $y_0$
- TCX: Tính $\lim_{x \to \pm\infty} [f(x) – (ax+b)]$ phải bằng 0
Q6: Hàm nào thường có tiệm cận đứng?
A:
- Hàm phân thức: $\frac{P(x)}{Q(x)}$
- Hàm logarit: $\ln(g(x))$
- Hàm lượng giác: $\tan x$, $\cot x$
- Hàm $\frac{1}{g(x)}$
Q7: Có công thức nhớ nhanh không?
A: Có! Với $y = \frac{ax+b}{cx+d}$:
- TCĐ: $x = -\frac{d}{c}$
- TCN: $y = \frac{a}{c}$

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
