Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU
- 1. Diện tích hình phẳng trong tích phân là gì?
- 2. Tại sao dùng tích phân để tính diện tích?
- 3. Cấu trúc bài viết
- II. CÔNG THỨC TÍCH PHÂN TÍNH DIỆN TÍCH
- CÔNG THỨC 1: Diện tích giới hạn bởi đồ thị hàm số và trục Ox
- Trường hợp đặc biệt:
- CÔNG THỨC 2: Diện tích giới hạn bởi hai đồ thị hàm số
- Trường hợp đặc biệt:
- Lưu ý quan trọng:
- III. CÁC DẠNG BÀI TẬP THƯỜNG GẶP
- Dạng 1: Diện tích giới hạn bởi parabol và trục Ox
- Dạng 2: Diện tích giới hạn bởi đường cong và đường thẳng
- Dạng 3: Diện tích hình phẳng với hàm lượng giác
- Dạng 4: Diện tích với hàm mũ/logarit
- Dạng 5: Diện tích giữa hai parabol
- IV. BÀI TẬP THỰC TẾ
- V. BẢNG TỔNG HỢP VÀ MẸO NHỚ
- Bảng tổng hợp công thức
- Mẹo giải nhanh
- VI. KẾT LUẬN
- Tổng kết
- Tài nguyên học thêm
I. GIỚI THIỆU
1. Diện tích hình phẳng trong tích phân là gì?
Định nghĩa: Diện tích hình phẳng trong tích phân là diện tích vùng giới hạn bởi đồ thị hàm số, trục hoành và các đường thẳng đứng.
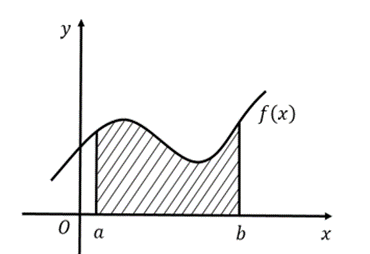
Phạm vi áp dụng:
- Chương trình Toán 12 – Ứng dụng tích phân
- Bài toán tính diện tích trong đề thi THPT Quốc gia
- Ứng dụng thực tế trong nhiều lĩnh vực
Ý nghĩa:
- Tính diện tích các hình phẳng bất kỳ (không chỉ hình học cơ bản)
- Ứng dụng trong vật lý: tính quãng đường, công, năng lượng
- Ứng dụng trong kinh tế: phân tích doanh thu, lợi nhuận
- Ứng dụng trong kỹ thuật: thiết kế, đo đạc
2. Tại sao dùng tích phân để tính diện tích?
Hình học cơ bản (vuông, chữ nhật, tam giác, hình tròn):
- Có công thức đơn giản đã biết
- Không cần dùng tích phân
Đường cong phức tạp (parabol, sin, cos, e^x, ln x):
- Không có công thức hình học đơn giản
- CẦN dùng tích phân để tính chính xác
Ứng dụng thực tế:
- Tính diện tích mặt hồ không đều
- Tính diện tích mặt cắt chi tiết máy
- Phân tích biểu đồ kinh tế (doanh thu, chi phí)
- Tính khối lượng công việc theo thời gian
3. Cấu trúc bài viết
Bài viết sẽ trình bày:
- 2 công thức tích phân cơ bản
- Phương pháp giải từng dạng bài
- 10 ví dụ minh họa chi tiết
- 8 bài tập thực tế có lời giải
- Bảng tổng hợp và mẹo nhớ
II. CÔNG THỨC TÍCH PHÂN TÍNH DIỆN TÍCH
CÔNG THỨC 1: Diện tích giới hạn bởi đồ thị hàm số và trục Ox
Điều kiện: Hàm số $y = f(x)$ liên tục trên $[a; b]$
Công thức:
$$S = \int_a^b |f(x)| , dx$$
Giải thích:
- Vùng tính: Giữa đồ thị $y = f(x)$ và trục Ox, từ $x = a$ đến $x = b$
- Dùng trị tuyệt đối vì diện tích luôn dương
- Nếu $f(x)$ ở dưới trục Ox, tích phân âm → cần trị tuyệt đối
Trường hợp đặc biệt:
a) Khi $f(x) \geq 0$ trên $[a; b]$ (đồ thị nằm hoàn toàn phía trên trục Ox)
$$S = \int_a^b f(x) , dx$$
Ví dụ 1: Tính diện tích hình phẳng giới hạn bởi $y = x^2$, trục Ox, $x = 0$, $x = 2$
Lời giải:
- Ta có: $x^2 \geq 0$ với mọi $x \in [0; 2]$
- Diện tích: $$S = \int_0^2 x^2 , dx = \left[\frac{x^3}{3}\right]_0^2 = \frac{8}{3} – 0 = \frac{8}{3}$$ (đvdt)
Đáp số: $\frac{8}{3}$ đơn vị diện tích
b) Khi $f(x) \leq 0$ trên $[a; b]$ (đồ thị nằm hoàn toàn phía dưới trục Ox)
$$S = -\int_a^b f(x) , dx = \left|\int_a^b f(x) , dx\right|$$
Ví dụ 2: Tính diện tích hình phẳng giới hạn bởi $y = x^2 – 4$, trục Ox, $x = 0$, $x = 1$
Lời giải:
- Trên $[0; 1]$: $x^2 – 4 < 0$ (đồ thị nằm dưới trục Ox)
- Diện tích: $$S = -\int_0^1 (x^2 – 4) , dx = -\left[\frac{x^3}{3} – 4x\right]_0^1$$ $$= -\left(\frac{1}{3} – 4\right) = -\left(-\frac{11}{3}\right) = \frac{11}{3}$$ (đvdt)
Đáp số: $\frac{11}{3}$ đơn vị diện tích
c) Khi $f(x)$ đổi dấu trên $[a; b]$ (đồ thị cắt trục Ox)
Phương pháp:
- Tìm nghiệm của $f(x) = 0$ trên $(a; b)$ để xác định điểm đổi dấu
- Chia thành các khoảng con
- Tính diện tích từng phần và cộng lại
$$S = \int_a^{c_1} |f(x)| , dx + \int_{c_1}^{c_2} |f(x)| , dx + … + \int_{c_n}^b |f(x)| , dx$$
Ví dụ 3: Tính diện tích hình phẳng giới hạn bởi $y = x^2 – 4x + 3$, trục Ox, $x = 0$, $x = 4$
Lời giải:
- Tìm nghiệm: $x^2 – 4x + 3 = 0 \Rightarrow (x-1)(x-3) = 0 \Rightarrow x = 1$ hoặc $x = 3$
- Xét dấu:
- $x \in [0; 1]$: $f(x) > 0$ (thử $x = 0.5$)
- $x \in [1; 3]$: $f(x) < 0$ (thử $x = 2$)
- $x \in [3; 4]$: $f(x) > 0$ (thử $x = 3.5$)
- Diện tích: $$S = \int_0^1 (x^2 – 4x + 3) , dx – \int_1^3 (x^2 – 4x + 3) , dx + \int_3^4 (x^2 – 4x + 3) , dx$$
$$= \left[\frac{x^3}{3} – 2x^2 + 3x\right]_0^1 – \left[\frac{x^3}{3} – 2x^2 + 3x\right]_1^3 + \left[\frac{x^3}{3} – 2x^2 + 3x\right]_3^4$$
$$= \left(\frac{1}{3} – 2 + 3\right) – \left[\left(9 – 18 + 9\right) – \left(\frac{1}{3} – 2 + 3\right)\right] + \left[\left(\frac{64}{3} – 32 + 12\right) – (9 – 18 + 9)\right]$$
$$= \frac{4}{3} – \left(0 – \frac{4}{3}\right) + \left(\frac{4}{3} – 0\right) = \frac{4}{3} + \frac{4}{3} + \frac{4}{3} = 4$$ (đvdt)
Đáp số: 4 đơn vị diện tích
CÔNG THỨC 2: Diện tích giới hạn bởi hai đồ thị hàm số
Điều kiện: Hàm số $y = f(x)$ và $y = g(x)$ liên tục trên $[a; b]$
Công thức:
$$S = \int_a^b |f(x) – g(x)| , dx$$
Giải thích:
- Vùng tính: Giữa hai đồ thị $y = f(x)$ và $y = g(x)$, từ $x = a$ đến $x = b$
- Trị tuyệt đối đảm bảo diện tích dương
Trường hợp đặc biệt:
a) Khi $f(x) \geq g(x)$ trên $[a; b]$ (đồ thị $f$ nằm hoàn toàn phía trên $g$)
$$S = \int_a^b [f(x) – g(x)] , dx$$
Ví dụ 4: Tính diện tích hình phẳng giới hạn bởi $y = x^2 + 1$ và $y = x + 1$, từ $x = 0$ đến $x = 2$
Lời giải:
- So sánh: $x^2 + 1 \geq x + 1 \Leftrightarrow x^2 \geq x \Leftrightarrow x(x-1) \geq 0$
- Với $x \in [0; 1]$: $x^2 + 1 \leq x + 1$
- Với $x \in [1; 2]$: $x^2 + 1 \geq x + 1$
- Diện tích: $$S = \int_0^1 [(x+1) – (x^2+1)] , dx + \int_1^2 [(x^2+1) – (x+1)] , dx$$ $$= \int_0^1 (x – x^2) , dx + \int_1^2 (x^2 – x) , dx$$ $$= \left[\frac{x^2}{2} – \frac{x^3}{3}\right]_0^1 + \left[\frac{x^3}{3} – \frac{x^2}{2}\right]_1^2$$ $$= \left(\frac{1}{2} – \frac{1}{3}\right) + \left[\left(\frac{8}{3} – 2\right) – \left(\frac{1}{3} – \frac{1}{2}\right)\right]$$ $$= \frac{1}{6} + \frac{5}{6} = 1$$ (đvdt)
Đáp số: 1 đơn vị diện tích
b) Khi hai đồ thị cắt nhau trên $[a; b]$
Phương pháp:
- Giải phương trình $f(x) = g(x)$ để tìm giao điểm
- Chia thành các khoảng con
- Xác định hàm nào lớn hơn trên mỗi khoảng
- Tính diện tích từng phần
Ví dụ 5: Tính diện tích hình phẳng giới hạn bởi $y = x^2$ và $y = 2x$
Lời giải:
- Tìm giao điểm: $x^2 = 2x \Rightarrow x(x-2) = 0 \Rightarrow x = 0$ hoặc $x = 2$
- Trên $[0; 2]$: $2x \geq x^2$ (thử $x = 1$: $2 > 1$ ✓)
- Diện tích: $$S = \int_0^2 (2x – x^2) , dx = \left[x^2 – \frac{x^3}{3}\right]_0^2 = 4 – \frac{8}{3} = \frac{4}{3}$$ (đvdt)
Đáp số: $\frac{4}{3}$ đơn vị diện tích
Lưu ý quan trọng:
1. Khi nào dùng trị tuyệt đối?
- Nếu không chắc dấu của $f(x)$ hoặc $f(x) – g(x)$: BẮT BUỘC dùng
- Nếu đã xét dấu rõ ràng: Có thể bỏ trị tuyệt đối và đổi dấu tích phân khi cần
2. Cách xử lý trị tuyệt đối: $$\int_a^b |f(x)| , dx = \int_a^c f(x) , dx – \int_c^d f(x) , dx + \int_d^b f(x) , dx$$ (Với $c$, $d$ là nghiệm của $f(x) = 0$, và đổi dấu tương ứng)
3. Công thức rút gọn:
- Nếu $f(x)$ không đổi dấu trên $[a; b]$: $$\int_a^b |f(x)| , dx = \left|\int_a^b f(x) , dx\right|$$
4. Đơn vị:
- Nếu đề không cho đơn vị cụ thể, viết “đơn vị diện tích” (đvdt)
- Nếu có đơn vị trục tọa độ (cm, m), diện tích tính theo cm², m²
III. CÁC DẠNG BÀI TẬP THƯỜNG GẶP
Dạng 1: Diện tích giới hạn bởi parabol và trục Ox
Bài tập 1: Tính diện tích hình phẳng giới hạn bởi $(P): y = -x^2 + 4x – 3$, trục Ox
Lời giải:
- Tìm giao điểm với Ox: $-x^2 + 4x – 3 = 0 \Rightarrow x^2 – 4x + 3 = 0$
- $(x-1)(x-3) = 0 \Rightarrow x = 1$ hoặc $x = 3$
- Trên $[1; 3]$: $-x^2 + 4x – 3 \geq 0$ (parabol quay bề lõm xuống, đỉnh $x = 2$)
- Diện tích: $$S = \int_1^3 (-x^2 + 4x – 3) , dx = \left[-\frac{x^3}{3} + 2x^2 – 3x\right]_1^3$$ $$= \left(-9 + 18 – 9\right) – \left(-\frac{1}{3} + 2 – 3\right) = 0 – \left(-\frac{4}{3}\right) = \frac{4}{3}$$ (đvdt)
Đáp số: $\frac{4}{3}$ đơn vị diện tích
Dạng 2: Diện tích giới hạn bởi đường cong và đường thẳng
Bài tập 2: Tính diện tích hình phẳng giới hạn bởi $y = x^3$ và $y = x$
Lời giải:
- Tìm giao điểm: $x^3 = x \Rightarrow x(x^2 – 1) = 0 \Rightarrow x \in {-1, 0, 1}$
- Xét trên $[-1; 0]$: $x^3 \leq x$ (thử $x = -0.5$: $-0.125 \leq -0.5$ ✓)
- Xét trên $[0; 1]$: $x^3 \leq x$ (thử $x = 0.5$: $0.125 \leq 0.5$ ✓)
- Do tính đối xứng qua gốc tọa độ: $$S = 2\int_0^1 (x – x^3) , dx = 2\left[\frac{x^2}{2} – \frac{x^4}{4}\right]_0^1$$ $$= 2\left(\frac{1}{2} – \frac{1}{4}\right) = 2 \times \frac{1}{4} = \frac{1}{2}$$ (đvdt)
Đáp số: $\frac{1}{2}$ đơn vị diện tích
Dạng 3: Diện tích hình phẳng với hàm lượng giác
Bài tập 3: Tính diện tích hình phẳng giới hạn bởi $y = \sin x$, trục Ox, từ $x = 0$ đến $x = \pi$
Lời giải:
- Trên $[0; \pi]$: $\sin x \geq 0$
- Diện tích: $$S = \int_0^\pi \sin x , dx = [-\cos x]_0^\pi = -\cos\pi – (-\cos 0) = -(-1) + 1 = 2$$ (đvdt)
Đáp số: 2 đơn vị diện tích
Dạng 4: Diện tích với hàm mũ/logarit
Bài tập 4: Tính diện tích hình phẳng giới hạn bởi $y = e^x$, trục Ox, $x = 0$, $x = 1$
Lời giải:
- Trên $[0; 1]$: $e^x > 0$
- Diện tích: $$S = \int_0^1 e^x , dx = [e^x]_0^1 = e – 1$$ (đvdt)
Đáp số: $(e – 1)$ đơn vị diện tích ≈ 1.718 đvdt
Dạng 5: Diện tích giữa hai parabol
Bài tập 5: Tính diện tích hình phẳng giới hạn bởi $y = x^2$ và $y = -x^2 + 2$
Lời giải:
- Tìm giao điểm: $x^2 = -x^2 + 2 \Rightarrow 2x^2 = 2 \Rightarrow x = \pm 1$
- Trên $[-1; 1]$: $-x^2 + 2 \geq x^2$ (thử $x = 0$: $2 > 0$ ✓)
- Do tính đối xứng: $$S = 2\int_0^1 [(-x^2 + 2) – x^2] , dx = 2\int_0^1 (2 – 2x^2) , dx$$ $$= 2\left[2x – \frac{2x^3}{3}\right]_0^1 = 2\left(2 – \frac{2}{3}\right) = 2 \times \frac{4}{3} = \frac{8}{3}$$ (đvdt)
Đáp số: $\frac{8}{3}$ đơn vị diện tích
IV. BÀI TẬP THỰC TẾ
Bài tập thực tế 1: Tính diện tích mặt hồ
Đề bài: Một mặt hồ có dạng hình phẳng giới hạn bởi đường cong $y = -\frac{1}{100}x^2 + 4$ (đơn vị: mét) và trục Ox. Tính diện tích mặt hồ.
Lời giải:
- Tìm giao điểm với Ox: $-\frac{1}{100}x^2 + 4 = 0 \Rightarrow x^2 = 400 \Rightarrow x = \pm 20$
- Do tính đối xứng: $$S = 2\int_0^{20} \left(-\frac{1}{100}x^2 + 4\right) dx = 2\left[-\frac{x^3}{300} + 4x\right]_0^{20}$$ $$= 2\left(-\frac{8000}{300} + 80\right) = 2\left(-\frac{80}{3} + 80\right) = 2 \times \frac{160}{3} = \frac{320}{3} \approx 106.67 \text{ m}^2$$
Đáp số: $\frac{320}{3}$ m² ≈ 106.67 m²
Ứng dụng: Tính lượng nước trong hồ, chi phí xây dựng, làm sạch hồ.
Bài tập thực tế 2: Tính diện tích mặt cắt cầu
Đề bài: Mặt cắt của một cây cầu có dạng parabol $y = -0.02x^2 + 1.8$ (m). Hai đầu cầu tiếp đất (y = 0). Tính diện tích mặt cắt.
Lời giải:
- Tìm hai đầu cầu: $-0.02x^2 + 1.8 = 0 \Rightarrow x^2 = 90 \Rightarrow x = \pm 3\sqrt{10}$
- Diện tích: $$S = 2\int_0^{3\sqrt{10}} (-0.02x^2 + 1.8) , dx = 2\left[-\frac{0.02x^3}{3} + 1.8x\right]_0^{3\sqrt{10}}$$ $$= 2\left[-\frac{0.02 \times 90 \times 3\sqrt{10}}{3} + 1.8 \times 3\sqrt{10}\right]$$ $$= 2\left[-1.8\sqrt{10} + 5.4\sqrt{10}\right] = 2 \times 3.6\sqrt{10} = 7.2\sqrt{10} \approx 22.77 \text{ m}^2$$
Đáp số: $7.2\sqrt{10}$ m² ≈ 22.77 m²
Ứng dụng: Tính vật liệu xây dựng, kiểm tra thiết kế.
Bài tập thực tế 3: Phân tích biểu đồ tăng trưởng
Đề bài: Doanh thu của công ty theo tháng được mô hình hóa bởi $f(t) = 2t + 5$ (triệu đồng/tháng) và chi phí bởi $g(t) = t^2 + 1$, với $t \in [0; 3]$ (tháng). Tính tổng lợi nhuận trong 3 tháng đầu.
Lời giải:
- Lợi nhuận = Doanh thu – Chi phí = $f(t) – g(t) = 2t + 5 – t^2 – 1 = -t^2 + 2t + 4$
- Xét dấu: $-t^2 + 2t + 4 > 0$ với $t \in [0; 3]$ (đỉnh parabol tại $t = 1$, giá trị đỉnh = 5 > 0)
- Tổng lợi nhuận: $$S = \int_0^3 (-t^2 + 2t + 4) , dt = \left[-\frac{t^3}{3} + t^2 + 4t\right]_0^3$$ $$= -9 + 9 + 12 = 12 \text{ triệu đồng}$$
Đáp số: 12 triệu đồng
Ứng dụng: Phân tích tài chính, dự báo kinh doanh.
Bài tập thực tế 4: Tính diện tích vườn hình elip
Đề bài: Một khu vườn có biên dạng elip $\frac{x^2}{16} + \frac{y^2}{9} = 1$ (m). Tính diện tích khu vườn.
Lời giải:
- Từ phương trình elip: $y = 3\sqrt{1 – \frac{x^2}{16}}$ (nửa trên)
- Diện tích elip = $\pi ab$ với $a = 4$, $b = 3$
- $S = \pi \times 4 \times 3 = 12\pi \approx 37.7$ m²
Đáp số: $12\pi$ m² ≈ 37.7 m²
Ứng dụng: Thiết kế cảnh quan, tính lượng cỏ trồng.
Bài tập thực tế 5: Khối lượng công việc theo thời gian
Đề bài: Tốc độ hoàn thành công việc (sản phẩm/giờ) được cho bởi $v(t) = 20 + 5\sin(\frac{\pi t}{4})$ với $t \in [0; 8]$ (giờ). Tính tổng số sản phẩm hoàn thành trong 8 giờ.
Lời giải: $$S = \int_0^8 \left(20 + 5\sin\frac{\pi t}{4}\right) dt = \left[20t – \frac{5 \times 4}{\pi}\cos\frac{\pi t}{4}\right]_0^8$$ $$= \left[20 \times 8 – \frac{20}{\pi}\cos 2\pi\right] – \left[0 – \frac{20}{\pi}\cos 0\right]$$ $$= 160 – \frac{20}{\pi} + \frac{20}{\pi} = 160 \text{ sản phẩm}$$
Đáp số: 160 sản phẩm
Ứng dụng: Quản lý sản xuất, tối ưu hóa quy trình.
Bài tập thực tế 6: Tính diện tích mảnh đất không đều
Đề bài: Một mảnh đất có hai biên song song cách nhau 10m. Biên phía Bắc thẳng (y = 10), biên phía Nam có dạng $y = x^2 – 5x + 10$, với $x \in [0; 5]$ (m). Tính diện tích.
Lời giải: $$S = \int_0^5 [10 – (x^2 – 5x + 10)] , dx = \int_0^5 (-x^2 + 5x) , dx$$ $$= \left[-\frac{x^3}{3} + \frac{5x^2}{2}\right]_0^5 = -\frac{125}{3} + \frac{125}{2} = \frac{125}{6} \approx 20.83 \text{ m}^2$$
Đáp số: $\frac{125}{6}$ m² ≈ 20.83 m²
Ứng dụng: Thẩm định giá đất, quy hoạch xây dựng.
Bài tập thực tế 7: Tính diện tích biển quảng cáo
Đề bài: Một biển quảng cáo có dạng hình phẳng giới hạn bởi $y = \sqrt{x}$ và $y = \frac{x}{4}$, với $x \in [0; 4]$ (m). Tính diện tích để sơn.
Lời giải:
- Tìm giao điểm: $\sqrt{x} = \frac{x}{4} \Rightarrow 4\sqrt{x} = x \Rightarrow x = 16$ (ngoài [0,4])
- Trên [0; 4]: $\sqrt{x} \geq \frac{x}{4}$ (kiểm tra tại x = 1: $1 > 0.25$ ✓) $$S = \int_0^4 \left(\sqrt{x} – \frac{x}{4}\right) dx = \left[\frac{2x^{3/2}}{3} – \frac{x^2}{8}\right]_0^4$$ $$= \frac{2 \times 8}{3} – 2 = \frac{16}{3} – 2 = \frac{10}{3} \approx 3.33 \text{ m}^2$$
Đáp số: $\frac{10}{3}$ m² ≈ 3.33 m²
Ứng dụng: Tính chi phí sơn, thiết kế quảng cáo.
Bài tập thực tế 8: Phân tích tiêu thụ nhiên liệu
Đề bài: Tốc độ tiêu thụ nhiên liệu của xe (lít/km) theo vận tốc v (km/h) là $f(v) = \frac{v}{100} + \frac{1600}{v}$. Tính lượng nhiên liệu tiêu thụ khi vận tốc thay đổi từ 40 km/h đến 100 km/h (mỗi vận tốc trong 1 km).
Lời giải: $$S = \int_{40}^{100} \left(\frac{v}{100} + \frac{1600}{v}\right) dv = \left[\frac{v^2}{200} + 1600\ln v\right]_{40}^{100}$$ $$= \left(\frac{10000}{200} + 1600\ln 100\right) – \left(\frac{1600}{200} + 1600\ln 40\right)$$ $$= 50 + 1600\ln\frac{100}{40} = 50 + 1600\ln 2.5 \approx 50 + 1466 \approx 1516 \text{ lít}$$
Đáp số: Khoảng 1516 lít
Ứng dụng: Tối ưu vận tốc, tiết kiệm nhiên liệu.
V. BẢNG TỔNG HỢP VÀ MẸO NHỚ
Bảng tổng hợp công thức
| Dạng | Công thức | Điều kiện |
|---|---|---|
| Đồ thị – Trục Ox | $S = \int_a^b |f(x)| , dx$ | $f(x)$ liên tục |
| Hai đồ thị | $S = \int_a^b |f(x) – g(x)| , dx$ | $f(x)$, $g(x)$ liên tục |
| $f(x) \geq 0$ | $S = \int_a^b f(x) , dx$ | Đồ thị trên trục Ox |
| $f(x) \leq 0$ | $S = -\int_a^b f(x) , dx$ | Đồ thị dưới trục Ox |
| $f(x)$ không đổi dấu | $S = \left|\int_a^b f(x) , dx\right|$ | Không cắt trục |
Mẹo giải nhanh
1. Quy trình 5 bước chuẩn:
- Bước 1: Vẽ hình (nếu có thể) để hình dung vùng tính
- Bước 2: Tìm giao điểm (nghiệm phương trình)
- Bước 3: Xét dấu trên từng khoảng
- Bước 4: Lập công thức tích phân (có/không trị tuyệt đối)
- Bước 5: Tính tích phân và kết luận
2. Mẹo xét dấu nhanh:
- Thử 1 giá trị cụ thể trong khoảng
- Parabol: Xét hệ số $a$ và vị trí đỉnh
- Tích $(x-a)(x-b)$: Dùng bảng xét dấu
3. Mẹo tính nhanh với tính chẵn/lẻ:
- Nếu $f(x)$ chẵn: $\int_{-a}^a f(x) , dx = 2\int_0^a f(x) , dx$
- Nếu $f(x)$ lẻ: $\int_{-a}^a f(x) , dx = 0$
4. Các công thức nguyên hàm cần nhớ:
| Hàm số | Nguyên hàm |
|---|---|
| $x^n$ | $\frac{x^{n+1}}{n+1} + C$ |
| $e^x$ | $e^x + C$ |
| $\sin x$ | $-\cos x + C$ |
| $\cos x$ | $\sin x + C$ |
| $\frac{1}{x}$ | $\ln|x| + C$ |
| $\frac{1}{ax+b}$ | $\frac{1}{a}\ln|ax+b| + C$ |
VI. KẾT LUẬN
Tổng kết
Bài viết đã hệ thống hóa công thức tính diện tích hình phẳng bằng tích phân:
2 công thức cốt lõi:
- $S = \int_a^b |f(x)| , dx$ (đồ thị – trục Ox)
- $S = \int_a^b |f(x) – g(x)| , dx$ (hai đồ thị)
Phương pháp xử lý:
- Xét dấu → Chia khoảng → Bỏ trị tuyệt đối
- Tìm giao điểm → Xác định vùng → Tính diện tích
10 ví dụ minh họa từ cơ bản đến nâng cao
8 bài tập thực tế ứng dụng trong:
- Kiến trúc (mặt hồ, cầu, đất)
- Kinh tế (doanh thu, lợi nhuận)
- Kỹ thuật (nhiên liệu, sản xuất)
Tài nguyên học thêm
Xem thêm:
- Công thức tích phân cơ bản – Đầy đủ nhất
- Phương pháp tích phân từng phần và đổi biến
- Ứng dụng tích phân tính thể tích vật thể tròn xoay

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
