Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ LỰC CĂNG DÂY
- 1. Lực căng dây là gì?
- 2. Tính chất của lực căng dây
- II. CÔNG THỨC LỰC CĂNG DÂY CƠ BẢN
- 1. Vật treo thẳng đứng đứng yên
- 2. Vật chuyển động thẳng đứng với gia tốc
- 3. Các trường hợp đặc biệt
- 4. Công thức nhớ nhanh
- III. LỰC CĂNG DÂY TRÊN MẶT PHẲNG NGHIÊNG
- 1. Vật đứng yên trên mặt phẳng nghiêng
- 2. Có ma sát
- IV. HỆ HAI VẬT NỐI DÂY QUA RÒNG RỌC
- 1. Hệ hai vật treo thẳng đứng (Máy Atwood)
- 2. Một vật trên mặt ngang, một vật treo
- 3. Hai vật trên mặt phẳng nghiêng
- V. LỰC CĂNG DÂY TRONG CHUYỂN ĐỘNG TRÒN
- 1. Vật chuyển động tròn đều thẳng đứng
- 2. Con lắc đơn
- VI. BẢNG CÔNG THỨC TÓM TẮT
- A. Vật treo thẳng đứng
- B. Mặt phẳng nghiêng
- C. Hệ hai vật
- D. Chuyển động tròn
- VII. BÀI TẬP MẪU
- VIII. PHƯƠNG PHÁP GIẢI NHANH
- 1. Các bước giải bài toán lực căng dây
- 2. Mẹo nhớ nhanh
- IX. MẸO VÀ LƯU Ý
- 1. Các sai lầm thường gặp
- 2. Lưu ý quan trọng
- 3. Kiểm tra nhanh kết quả
- X. KẾT LUẬN
- Công thức quan trọng nhất
I. GIỚI THIỆU VỀ LỰC CĂNG DÂY
1. Lực căng dây là gì?
Định nghĩa: Lực căng dây là lực mà sợi dây tác dụng lên vật được treo hoặc nối với dây. Đây là một trong những lực quan trọng thường gặp trong bài toán cơ học.
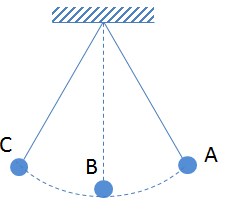
Ký hiệu:
- $\vec{T}$ (từ tiếng Anh: Tension – sức căng)
- Đôi khi còn ký hiệu là $\vec{F_c}$ (lực căng)
Đặc điểm:
- Hướng: Lực căng dây luôn dọc theo phương của dây, hướng từ vật ra xa điểm treo hoặc điểm giữ dây
- Điểm đặt: Tại điểm tiếp xúc giữa dây và vật
- Bản chất: Là phản lực của dây khi bị kéo căng
2. Tính chất của lực căng dây
Giả thiết quan trọng trong bài toán:
Để đơn giản hóa, trong hầu hết các bài toán vật lý phổ thông, ta giả thiết dây là dây lý tưởng với các tính chất:
Dây không dãn: Độ dài dây không thay đổi khi chịu lực kéo
Dây không có khối lượng: Hoặc khối lượng dây rất nhỏ so với khối lượng vật, có thể bỏ qua
Dây chỉ chịu kéo, không chịu nén: Dây chỉ có thể bị căng, không thể bị ép
Dây không bị đứt: Lực căng không vượt quá giới hạn bền của dây
Tính chất quan trọng:
Tính chất 1: Lực căng truyền nguyên vẹn qua dây
- Nếu dây không có khối lượng và không có ma sát, lực căng tại mọi điểm trên dây đều bằng nhau
Tính chất 2: Hai đầu dây có độ lớn lực căng bằng nhau
- Lực căng tại điểm treo = Lực căng tại điểm nối với vật (nếu dây lý tưởng)
Tính chất 3: Lực căng có thể thay đổi
- Phụ thuộc vào trạng thái chuyển động của vật (đứng yên, chuyển động đều, chuyển động có gia tốc)
II. CÔNG THỨC LỰC CĂNG DÂY CƠ BẢN
1. Vật treo thẳng đứng đứng yên
Trường hợp đơn giản nhất: Vật có khối lượng $m$ treo đứng yên bằng một sợi dây thẳng đứng.
Công thức:
$$\boxed{T = P = mg}$$
Trong đó:
- $T$: Lực căng dây (N – Newton)
- $P$: Trọng lượng vật (N)
- $m$: Khối lượng vật (kg)
- $g$: Gia tốc trọng trường ($g = 10$ m/s² hoặc 9.8 m/s²)
Giải thích vật lý:
Vật đứng yên nên ở trạng thái cân bằng. Theo điều kiện cân bằng: $$\vec{T} + \vec{P} = \vec{0}$$
Chiếu lên phương thẳng đứng (chọn chiều dương hướng lên): $$T – P = 0$$ $$T = P = mg$$
Ví dụ 1: Một vật có khối lượng $m = 2$ kg treo đứng yên. Tính lực căng dây? (Lấy $g = 10$ m/s²)
Lời giải: $$T = mg = 2 \times 10 = 20 \text{ N}$$
Đáp án: Lực căng dây là 20N.
2. Vật chuyển động thẳng đứng với gia tốc
Trường hợp tổng quát: Vật chuyển động thẳng đứng với gia tốc $a$.
Công thức:
$$\boxed{T = m(g + a)}$$
Trong đó:
- $a$: Gia tốc của vật (m/s²)
- Quy ước dấu: Chọn chiều dương hướng lên
- $a > 0$: Gia tốc hướng lên → $T > mg$
- $a < 0$: Gia tốc hướng xuống → $T < mg$
- $a = 0$: Đứng yên hoặc chuyển động đều → $T = mg$
Chứng minh từ định luật Newton II:
Áp dụng định luật II Newton: $\vec{F} = m\vec{a}$
Chiếu lên phương thẳng đứng (chiều dương hướng lên): $$T – P = ma$$ $$T – mg = ma$$ $$T = mg + ma = m(g + a)$$
Ví dụ 2: Vật khối lượng $m = 3$ kg chuyển động thẳng đứng với gia tốc $a = 2$ m/s² hướng lên. Tính lực căng dây? (Lấy $g = 10$ m/s²)
Lời giải: $$T = m(g + a) = 3(10 + 2) = 3 \times 12 = 36 \text{ N}$$
Đáp án: Lực căng dây là 36N.
3. Các trường hợp đặc biệt
a) Thang máy đi lên nhanh dần đều
Đặc điểm: Vận tốc hướng lên, gia tốc hướng lên ($a > 0$)
Công thức: $$\boxed{T = m(g + a) > mg}$$
Ví dụ 3: Một người có khối lượng $m = 50$ kg đứng trong thang máy đi lên nhanh dần đều với gia tốc $a = 2$ m/s². Tính lực mà sàn thang máy tác dụng lên người? (Lấy $g = 10$ m/s²)
Lời giải: $$T = m(g + a) = 50(10 + 2) = 50 \times 12 = 600 \text{ N}$$
Nhận xét: Người cảm thấy nặng hơn bình thường vì $T = 600N > mg = 500N$
b) Thang máy đi xuống nhanh dần đều (đang phanh)
Đặc điểm: Vận tốc hướng xuống, nhưng đang phanh nên gia tốc hướng lên ($a > 0$)
Công thức: $$\boxed{T = m(g + a) > mg}$$
Giải thích: Mặc dù đang đi xuống, nhưng do đang phanh (chậm dần), gia tốc ngược chiều với vận tốc, tức là hướng lên.
c) Thang máy đi lên chậm dần đều (đang phanh)
Đặc điểm: Vận tốc hướng lên, nhưng đang phanh nên gia tốc hướng xuống ($a < 0$)
Công thức: $$\boxed{T = m(g – |a|) < mg}$$
Ví dụ 4: Thang máy đi lên chậm dần đều với gia tốc có độ lớn $|a| = 2$ m/s². Người có khối lượng 60 kg. Tính lực mà sàn thang máy tác dụng lên người?
Lời giải: $$T = m(g – |a|) = 60(10 – 2) = 60 \times 8 = 480 \text{ N}$$
Nhận xét: Người cảm thấy nhẹ hơn bình thường vì $T = 480N < mg = 600N$
d) Thang máy đi xuống chậm dần đều
Đặc điểm: Vận tốc hướng xuống, gia tốc hướng xuống ($a < 0$)
Công thức: $$\boxed{T = m(g – |a|) < mg}$$
e) Rơi tự do
Đặc điểm: Gia tốc bằng gia tốc trọng trường, hướng xuống: $a = -g$
Công thức: $$\boxed{T = m(g – g) = 0}$$
Ý nghĩa: Đây là trạng thái không trọng lượng (weightlessness). Dây không căng, vật rơi tự do.
Ví dụ: Thang máy bị đứt cáp và rơi tự do → người trong thang máy cảm thấy mất trọng lượng, lơ lửng trong không khí.
4. Công thức nhớ nhanh
Quy ước dấu quan trọng:
- Chọn chiều dương hướng lên
- $a > 0$: gia tốc hướng lên
- $a < 0$: gia tốc hướng xuống
Công thức tổng quát:
$$\boxed{T = m(g + a)}$$
Với $a$ có dấu theo quy ước!
Bảng tổng hợp:
| Trạng thái chuyển động | Gia tốc | Lực căng | So sánh với mg |
|---|---|---|---|
| Đứng yên | $a = 0$ | $T = mg$ | $T = mg$ |
| Chuyển động đều | $a = 0$ | $T = mg$ | $T = mg$ |
| Lên nhanh dần | $a > 0$ | $T = m(g+a)$ | $T > mg$ |
| Xuống chậm dần | $a > 0$ | $T = m(g+a)$ | $T > mg$ |
| Lên chậm dần | $a < 0$ | $T = m(g-|a|)$ | $T < mg$ |
| Xuống nhanh dần | $a < 0$ | $T = m(g-|a|)$ | $T < mg$ |
| Rơi tự do | $a = -g$ | $T = 0$ | $T = 0$ |
III. LỰC CĂNG DÂY TRÊN MẶT PHẲNG NGHIÊNG
1. Vật đứng yên trên mặt phẳng nghiêng
Điều kiện: Vật đứng yên trên mặt phẳng nghiêng góc $\alpha$, giữ bằng dây song song với mặt phẳng nghiêng, không có ma sát.
Công thức:
$$\boxed{T = P\sin\alpha = mg\sin\alpha}$$
Giải thích:
Bước 1: Phân tích trọng lực thành hai thành phần:
- $P_t = P\sin\alpha = mg\sin\alpha$ (song song với mặt phẳng nghiêng, hướng xuống)
- $P_n = P\cos\alpha = mg\cos\alpha$ (vuông góc với mặt phẳng nghiêng)
Bước 2: Vật cân bằng theo phương song song với mặt phẳng: $$T = P_t = mg\sin\alpha$$
Ví dụ 5: Vật có khối lượng $m = 4$ kg đặt trên mặt phẳng nghiêng góc $\alpha = 30°$, giữ bằng dây song song với mặt phẳng. Tính lực căng dây? (Lấy $g = 10$ m/s², $\sin 30° = 0.5$)
Lời giải: $$T = mg\sin\alpha = 4 \times 10 \times \sin 30° = 40 \times 0.5 = 20 \text{ N}$$
Đáp án: Lực căng dây là 20N.
2. Có ma sát
a) Vật đứng yên
Khi có ma sát, lực ma sát nghỉ cùng với lực căng dây cân bằng với thành phần trọng lực theo mặt phẳng:
$$T + F_{ms} = P\sin\alpha$$
Suy ra: $$\boxed{T = mg\sin\alpha – F_{ms}}$$
Trong đó: $F_{ms}$ là lực ma sát nghỉ (có thể thay đổi từ 0 đến $F_{msmax} = \mu_s N = \mu_s mg\cos\alpha$)
b) Vật chuyển động lên
Lực ma sát trượt hướng ngược chiều chuyển động (hướng xuống):
$$T = m(g\sin\alpha + a) + F_{mst}$$
Với $F_{mst} = \mu_k mg\cos\alpha$
c) Vật chuyển động xuống
Lực ma sát trượt hướng ngược chiều chuyển động (hướng lên):
$$T + F_{mst} = m(g\sin\alpha – a)$$
IV. HỆ HAI VẬT NỐI DÂY QUA RÒNG RỌC
1. Hệ hai vật treo thẳng đứng (Máy Atwood)
Mô tả: Hai vật có khối lượng $m_1$ và $m_2$ ($m_1 > m_2$) được nối với nhau bằng dây không dãn, vắt qua ròng rọc cố định nhẹ.
Công thức lực căng:
$$\boxed{T = \frac{2m_1m_2}{m_1 + m_2} \cdot g}$$
Công thức gia tốc hệ:
$$\boxed{a = \frac{m_1 – m_2}{m_1 + m_2} \cdot g}$$
Chứng minh:
Bước 1: Viết phương trình Newton cho từng vật
Vật 1 (nặng hơn, đi xuống): $$m_1g – T = m_1a \quad (1)$$
Vật 2 (nhẹ hơn, đi lên): $$T – m_2g = m_2a \quad (2)$$
Bước 2: Cộng (1) và (2): $$(m_1 – m_2)g = (m_1 + m_2)a$$
$$a = \frac{m_1 – m_2}{m_1 + m_2} \cdot g$$
Bước 3: Thế $a$ vào (2): $$T = m_2g + m_2a = m_2g + m_2 \cdot \frac{m_1 – m_2}{m_1 + m_2} \cdot g$$
$$T = m_2g \left(1 + \frac{m_1 – m_2}{m_1 + m_2}\right) = m_2g \cdot \frac{2m_1}{m_1 + m_2}$$
$$T = \frac{2m_1m_2g}{m_1 + m_2}$$
Ví dụ 6: Hai vật có khối lượng $m_1 = 3$ kg và $m_2 = 2$ kg nối với nhau qua ròng rọc. Tính lực căng dây và gia tốc hệ? (Lấy $g = 10$ m/s²)
Lời giải:
Tính gia tốc: $$a = \frac{m_1 – m_2}{m_1 + m_2} \cdot g = \frac{3 – 2}{3 + 2} \times 10 = \frac{1}{5} \times 10 = 2 \text{ m/s}^2$$
Tính lực căng: $$T = \frac{2m_1m_2}{m_1 + m_2} \cdot g = \frac{2 \times 3 \times 2}{5} \times 10 = \frac{12}{5} \times 10 = 24 \text{ N}$$
Kiểm tra:
- Vật 1: $m_1g – T = 30 – 24 = 6 = 3 \times 2 = m_1a$ ✓
- Vật 2: $T – m_2g = 24 – 20 = 4 = 2 \times 2 = m_2a$ ✓
Đáp án:
- Gia tốc: $a = 2$ m/s²
- Lực căng: $T = 24$ N
2. Một vật trên mặt ngang, một vật treo
Mô tả: Vật 1 khối lượng $m_1$ đặt trên mặt ngang (có ma sát $\mu$), nối dây với vật 2 khối lượng $m_2$ treo thẳng đứng qua ròng rọc.
Gia tốc: $$\boxed{a = \frac{m_2g – \mu m_1g}{m_1 + m_2}}$$
Lực căng: $$\boxed{T = \frac{m_1m_2g(1 + \mu)}{m_1 + m_2}}$$
Chứng minh:
Vật 1 (trên mặt ngang): $$T – F_{ms} = m_1a$$ $$T – \mu m_1g = m_1a \quad (1)$$
Vật 2 (treo thẳng đứng): $$m_2g – T = m_2a \quad (2)$$
Cộng (1) và (2): $$m_2g – \mu m_1g = (m_1 + m_2)a$$
$$a = \frac{m_2g – \mu m_1g}{m_1 + m_2}$$
Thế vào (1): $$T = m_1a + \mu m_1g = m_1 \cdot \frac{m_2g – \mu m_1g}{m_1 + m_2} + \mu m_1g$$
$$T = \frac{m_1m_2g(1 + \mu)}{m_1 + m_2}$$
Ví dụ 7: Vật 1 có $m_1 = 2$ kg trên mặt ngang, hệ số ma sát $\mu = 0.2$. Vật 2 có $m_2 = 3$ kg treo thẳng đứng. Tính gia tốc và lực căng dây?
Lời giải:
Gia tốc: $$a = \frac{m_2g – \mu m_1g}{m_1 + m_2} = \frac{3 \times 10 – 0.2 \times 2 \times 10}{2 + 3} = \frac{30 – 4}{5} = \frac{26}{5} = 5.2 \text{ m/s}^2$$
Lực căng: $$T = \frac{m_1m_2g(1 + \mu)}{m_1 + m_2} = \frac{2 \times 3 \times 10 \times 1.2}{5} = \frac{72}{5} = 14.4 \text{ N}$$
Đáp án:
- Gia tốc: 5.2 m/s²
- Lực căng: 14.4 N
3. Hai vật trên mặt phẳng nghiêng
Mô tả: Hai vật trên hai mặt phẳng nghiêng góc $\alpha_1$ và $\alpha_2$ ở hai bên ròng rọc.
Gia tốc: $$\boxed{a = \frac{m_1\sin\alpha_1 – m_2\sin\alpha_2}{m_1 + m_2} \cdot g}$$
Lực căng: $$\boxed{T = \frac{m_1m_2(\sin\alpha_1 + \sin\alpha_2)}{m_1 + m_2} \cdot g}$$
V. LỰC CĂNG DÂY TRONG CHUYỂN ĐỘNG TRÒN
1. Vật chuyển động tròn đều thẳng đứng
Mô tả: Vật khối lượng $m$ chuyển động tròn đều trong mặt phẳng thẳng đứng với bán kính $R$, vận tốc $v$.
Tại điểm cao nhất:
Lực căng và trọng lực cùng hướng vào tâm:
$$\boxed{T_{min} = m\frac{v^2}{R} – mg}$$
Điều kiện để dây không bị chùng: $T \geq 0$
$$m\frac{v^2}{R} \geq mg$$
$$v \geq \sqrt{gR}$$
Vận tốc tối thiểu: $$v_{min} = \sqrt{gR}$$
Tại điểm thấp nhất:
Lực căng hướng lên, trọng lực hướng xuống:
$$\boxed{T_{max} = m\frac{v^2}{R} + mg}$$
Ví dụ 8: Vật có khối lượng $m = 0.5$ kg chuyển động tròn đều bán kính $R = 1$ m trong mặt phẳng thẳng đứng với vận tốc $v = 4$ m/s tại điểm thấp nhất. Tính lực căng dây?
Lời giải: $$T = m\frac{v^2}{R} + mg = 0.5 \times \frac{16}{1} + 0.5 \times 10$$ $$= 8 + 5 = 13 \text{ N}$$
Đáp án: Lực căng dây là 13N.
2. Con lắc đơn
Tại vị trí cân bằng:
$$\boxed{T = mg + m\frac{v^2}{l}}$$
Trong đó $l$ là chiều dài dây treo.
Tại vị trí biên (góc lệch $\alpha$):
$$\boxed{T = mg\cos\alpha}$$
VI. BẢNG CÔNG THỨC TÓM TẮT
A. Vật treo thẳng đứng
| Trường hợp | Công thức | Ghi chú |
|---|---|---|
| Đứng yên hoặc chuyển động đều | $T = mg$ | $a = 0$ |
| Chuyển động với gia tốc | $T = m(g + a)$ | $a$ có dấu |
| Đi lên nhanh dần | $T = m(g + a)$ | $a > 0$, $T > mg$ |
| Đi xuống chậm dần (phanh) | $T = m(g + a)$ | $a > 0$, $T > mg$ |
| Đi lên chậm dần (phanh) | $T = m(g – |a|)$ | $a < 0$, $T < mg$ |
| Đi xuống nhanh dần | $T = m(g – |a|)$ | $a < 0$, $T < mg$ |
| Rơi tự do | $T = 0$ | $a = -g$ |
B. Mặt phẳng nghiêng
| Trường hợp | Công thức | Điều kiện |
|---|---|---|
| Đứng yên, không ma sát | $T = mg\sin\alpha$ | Cân bằng |
| Đứng yên, có ma sát | $T = mg\sin\alpha – F_{ms}$ | $F_{ms} \leq \mu_s mg\cos\alpha$ |
| Chuyển động lên | $T = m(g\sin\alpha + a) + \mu_k mg\cos\alpha$ | Có gia tốc |
| Chuyển động xuống | $T + \mu_k mg\cos\alpha = m(g\sin\alpha – a)$ | Có gia tốc |
C. Hệ hai vật
| Loại hệ | Gia tốc | Lực căng |
|---|---|---|
| Hai vật treo (Atwood) | $a = \frac{m_1 – m_2}{m_1 + m_2}g$ | $T = \frac{2m_1m_2g}{m_1+m_2}$ |
| Một ngang, một treo | $a = \frac{m_2g – \mu m_1g}{m_1+m_2}$ | $T = \frac{m_1m_2g(1+\mu)}{m_1+m_2}$ |
| Hai vật trên mặt nghiêng | $a = \frac{m_1\sin\alpha_1 – m_2\sin\alpha_2}{m_1+m_2}g$ | $T = \frac{m_1m_2(\sin\alpha_1+\sin\alpha_2)}{m_1+m_2}g$ |
D. Chuyển động tròn
| Vị trí | Công thức | Ghi chú |
|---|---|---|
| Điểm cao nhất | $T = m\frac{v^2}{R} – mg$ | $v_{min} = \sqrt{gR}$ |
| Điểm thấp nhất | $T = m\frac{v^2}{R} + mg$ | $T_{max}$ |
| Con lắc – vị trí cân bằng | $T = mg + m\frac{v^2}{l}$ | $v$ lớn nhất |
| Con lắc – vị trí biên | $T = mg\cos\alpha$ | $v = 0$ |
VII. BÀI TẬP MẪU
Bài 1: Vật treo đứng yên
Đề bài: Một vật có khối lượng $m = 5$ kg treo đứng yên bằng dây. Tính lực căng dây? (Lấy $g = 10$ m/s²)
Lời giải:
Vật đứng yên nên: $$T = mg = 5 \times 10 = 50 \text{ N}$$
Đáp án: 50N.
Bài 2: Thang máy đi lên
Đề bài: Một người có khối lượng $m = 60$ kg đứng trong thang máy đang đi lên nhanh dần đều với gia tốc $a = 2$ m/s². Tính lực mà sàn thang máy tác dụng lên người? (Lấy $g = 10$ m/s²)
Lời giải:
Thang máy đi lên nhanh dần nên gia tốc hướng lên ($a > 0$): $$T = m(g + a) = 60(10 + 2) = 60 \times 12 = 720 \text{ N}$$
Đáp án: 720N.
Bài 3: Mặt phẳng nghiêng
Đề bài: Vật có khối lượng $m = 2$ kg đặt trên mặt phẳng nghiêng góc $\alpha = 30°$, được giữ bằng dây song song với mặt phẳng. Bỏ qua ma sát. Tính lực căng dây? (Lấy $g = 10$ m/s², $\sin 30° = 0.5$)
Lời giải: $$T = mg\sin\alpha = 2 \times 10 \times 0.5 = 10 \text{ N}$$
Đáp án: 10N.
Bài 4: Máy Atwood
Đề bài: Hai vật có khối lượng $m_1 = 4$ kg và $m_2 = 3$ kg được nối với nhau bằng dây vắt qua ròng rọc. Tính lực căng dây? (Lấy $g = 10$ m/s²)
Lời giải: $$T = \frac{2m_1m_2g}{m_1 + m_2} = \frac{2 \times 4 \times 3 \times 10}{4 + 3} = \frac{240}{7} \approx 34.3 \text{ N}$$
Đáp án: Khoảng 34.3N.
Bài 5: Chuyển động tròn
Đề bài: Vật có khối lượng $m = 0.2$ kg chuyển động tròn đều bán kính $R = 0.5$ m với vận tốc $v = 3$ m/s tại điểm thấp nhất của quỹ đạo tròn thẳng đứng. Tính lực căng dây? (Lấy $g = 10$ m/s²)
Lời giải: $$T = m\left(\frac{v^2}{R} + g\right) = 0.2\left(\frac{9}{0.5} + 10\right) = 0.2(18 + 10) = 0.2 \times 28 = 5.6 \text{ N}$$
Đáp án: 5.6N.
VIII. PHƯƠNG PHÁP GIẢI NHANH
1. Các bước giải bài toán lực căng dây
Bước 1: Vẽ hình và phân tích lực
- Vẽ sơ đồ hình học của bài toán
- Vẽ tất cả các lực tác dụng lên vật (trọng lực, lực căng, phản lực, ma sát…)
- Chọn hệ quy chiếu và chiều dương (thường hướng lên hoặc hướng chuyển động)
Bước 2: Viết phương trình định luật II Newton
- Cho từng vật: $\vec{F}_{hl} = m\vec{a}$
- Chiếu lên phương chuyển động
Bước 3: Giải hệ phương trình
- Nếu có nhiều vật: lập hệ phương trình
- Tìm gia tốc $a$ (nếu chưa biết)
- Tìm lực căng $T$
Bước 4: Kiểm tra kết quả
- Đơn vị có đúng không? (Newton – N)
- Kết quả có hợp lý không? ($T \geq 0$)
- Thử thế ngược vào phương trình để kiểm tra
2. Mẹo nhớ nhanh
Vật đứng yên: $T = mg$ (đơn giản nhất)
Có gia tốc: $T = m(g \pm a)$ (dấu phụ thuộc hướng gia tốc)
- Gia tốc hướng lên → dấu +
- Gia tốc hướng xuống → dấu –
Mặt nghiêng: Nhớ $\sin\alpha$ (không phải $\cos\alpha$)
- $T = mg\sin\alpha$
Máy Atwood: Công thức đặc biệt
- $T = \frac{2m_1m_2}{m_1+m_2}g$ (nhớ hệ số 2)
Chuyển động tròn:
- Điểm cao nhất: trừ $mg$
- Điểm thấp nhất: cộng $mg$
IX. MẸO VÀ LƯU Ý
1. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm dấu gia tốc
Sai: Thang máy đi xuống chậm dần → gia tốc hướng xuống ❌
Đúng: Thang máy đi xuống chậm dần (phanh) → gia tốc hướng lên ✓
Quy tắc: Gia tốc luôn cùng chiều với lực gây ra gia tốc, có thể ngược chiều vận tốc.
❌ SAI LẦM 2: Quên rằng lực căng truyền nguyên vẹn
Sai: Hai đầu dây có lực căng khác nhau ❌
Đúng: Hai đầu dây có độ lớn lực căng bằng nhau (nếu dây lý tưởng) ✓
❌ SAI LẦM 3: Nhầm $\sin$ và $\cos$ trên mặt nghiêng
Sai: $T = mg\cos\alpha$ ❌
Đúng: $T = mg\sin\alpha$ ✓
Cách nhớ: Thành phần song song với mặt nghiêng dùng $\sin\alpha$
❌ SAI LẦM 4: Quên các lực khác (ma sát, lực cản)
Lưu ý: Đọc kỹ đề xem có ma sát không, có lực cản không khí không?
2. Lưu ý quan trọng
Dây lý tưởng:
- Không dãn
- Không có khối lượng
- Lực căng truyền nguyên vẹn
Hướng lực căng:
- Luôn dọc theo dây
- Hướng ra xa điểm treo
- Có xu hướng kéo vật về phía điểm treo
Ròng rọc lý tưởng:
- Không có khối lượng
- Không có ma sát
- Chỉ làm thay đổi hướng lực, không làm thay đổi độ lớn $T$
Quan hệ giữa $T$ và $mg$:
- $T > mg$: Vật có xu hướng đi lên (hoặc đang bị kéo lên)
- $T = mg$: Vật cân bằng hoặc chuyển động đều
- $T < mg$: Vật có xu hướng đi xuống
- $T = 0$: Dây không căng (rơi tự do)
3. Kiểm tra nhanh kết quả
Điều kiện bắt buộc: $T \geq 0$ (lực căng không thể âm, dây không chịu nén)
Đơn vị: Lực căng đo bằng Newton (N)
So sánh:
- Nếu vật đứng yên: $T = mg$
- Nếu vật có gia tốc hướng lên: $T > mg$
- Nếu vật có gia tốc hướng xuống: $T < mg$
Giới hạn thực tế: Trong thực tế, dây có giới hạn bền. Nếu $T$ vượt quá giới hạn này, dây sẽ đứt.
X. KẾT LUẬN
Bài viết đã trình bày đầy đủ và chi tiết các công thức lực căng dây trong các trường hợp:
Vật treo thẳng đứng:
- Cơ bản: $T = m(g + a)$
- 7 trường hợp đặc biệt
Mặt phẳng nghiêng:
- $T = mg\sin\alpha$ (không ma sát)
- Công thức có ma sát
Hệ hai vật (Máy Atwood):
- $T = \frac{2m_1m_2g}{m_1+m_2}$
- Các biến thể khác
Chuyển động tròn:
- Điểm cao nhất: $T = m\frac{v^2}{R} – mg$
- Điểm thấp nhất: $T = m\frac{v^2}{R} + mg$
5 bài tập mẫu với lời giải chi tiết
Phương pháp giải 4 bước chuẩn
Mẹo nhớ và cảnh báo sai lầm
Công thức quan trọng nhất
Công thức vàng cho vật treo thẳng đứng:
$$\boxed{T = m(g + a)}$$
Với quy ước: Chọn chiều dương hướng lên, $a$ mang dấu theo quy ước.
Các trường hợp đặc biệt:
- $a = 0$: $T = mg$ (đứng yên/chuyển động đều)
- $a > 0$: $T > mg$ (gia tốc hướng lên)
- $a < 0$: $T < mg$ (gia tốc hướng xuống)
- $a = -g$: $T = 0$ (rơi tự do)

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
