Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ LỰC TỪ
- 1. Lực từ là gì?
- 2. Các đại lượng liên quan
- II. LỰC TỪ TÁC DỤNG LÊN DÂY DẪN (Lực Ampere)
- 1. Công thức lực từ tác dụng lên dây dẫn
- 2. Các trường hợp đặc biệt
- 3. Quy tắc bàn tay trái (xác định chiều lực)
- 4. Ví dụ minh họa
- 5. Ứng dụng: Động cơ điện
- III. LỰC LORENTZ (Lực từ tác dụng lên hạt mang điện)
- 1. Định nghĩa lực Lorentz
- 2. Các trường hợp đặc biệt
- 3. Quy tắc bàn tay trái cho lực Lorentz
- 4. Chuyển động của hạt điện trong từ trường
- 5. Ví dụ minh họa về lực Lorentz
- IV. SO SÁNH LỰC TỪ VÀ LỰC LORENTZ
- Bảng so sánh chi tiết
- Mối liên hệ giữa hai loại lực
- V. BẢNG CÔNG THỨC TỔNG HỢP
- A. Lực từ tác dụng lên dây dẫn
- B. Lực Lorentz tác dụng lên hạt điện
- C. Chuyển động tròn của hạt điện (v ⊥ B)
- D. Quy tắc bàn tay trái
- E. Đơn vị đo
- VI. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Lưu ý đặc biệt
- VII. BÀI TẬP MẪU
- VIII. KẾT LUẬN
- Lời khuyên học tập
I. GIỚI THIỆU VỀ LỰC TỪ
1. Lực từ là gì?
Định nghĩa: Lực từ là lực mà từ trường tác dụng lên vật mang điện chuyển động hoặc dây dẫn có dòng điện chạy qua. Đây là một trong những hiện tượng cơ bản của điện từ học.
Đặc điểm quan trọng:
- Lực từ luôn vuông góc với cả vector vận tốc (hoặc dòng điện) và vector từ trường
- Độ lớn lực từ phụ thuộc vào góc giữa chuyển động và từ trường
- Lực từ không sinh công (vì vuông góc với chuyển động)
Phân loại lực từ:
Loại 1: Lực từ tác dụng lên dây dẫn có dòng điện (còn gọi là lực Ampere)
- Tác dụng lên toàn bộ đoạn dây dẫn
- Phụ thuộc vào cường độ dòng điện và chiều dài dây
Loại 2: Lực từ tác dụng lên hạt mang điện (lực Lorentz)
- Tác dụng lên từng hạt riêng lẻ
- Phụ thuộc vào điện tích và vận tốc hạt
2. Các đại lượng liên quan
| Đại lượng | Ký hiệu | Đơn vị | Ý nghĩa |
|---|---|---|---|
| Lực từ | F | N (Newton) | Lực tác dụng lên dây dẫn |
| Lực Lorentz | $F_L$ | N (Newton) | Lực tác dụng lên hạt điện |
| Cảm ứng từ | B | T (Tesla) | Độ mạnh của từ trường |
| Cường độ dòng điện | I | A (Ampere) | Dòng điện chạy qua dây |
| Chiều dài dây | l | m (mét) | Chiều dài dây trong từ trường |
| Điện tích | q | C (Coulomb) | Điện tích của hạt |
| Vận tốc | v | m/s | Vận tốc của hạt |
| Góc | α | độ (°) hoặc rad | Góc giữa dòng/vận tốc và $\vec{B}$ |
| Khối lượng | m | kg | Khối lượng hạt |
II. LỰC TỪ TÁC DỤNG LÊN DÂY DẪN (Lực Ampere)
1. Công thức lực từ tác dụng lên dây dẫn
Công thức tổng quát:
Một dây dẫn thẳng có chiều dài l, có dòng điện I chạy qua, đặt trong từ trường đều có cảm ứng từ B:
$$\boxed{F = BIl\sin\alpha}$$
Trong đó:
- $F$: lực từ tác dụng lên dây dẫn (đơn vị: N – Newton)
- $B$: cảm ứng từ (đơn vị: T – Tesla)
- $I$: cường độ dòng điện qua dây (đơn vị: A – Ampere)
- $l$: chiều dài đoạn dây nằm trong từ trường (đơn vị: m – mét)
- $\alpha$: góc giữa chiều dòng điện (dây dẫn) và vector cảm ứng từ $\vec{B}$
Dạng vector: $$\vec{F} = I\vec{l} \times \vec{B}$$
(Tích có hướng của vector dòng điện và vector từ trường)
2. Các trường hợp đặc biệt
a) Dây dẫn vuông góc với từ trường (α = 90°):
Khi dây dẫn đặt vuông góc với các đường sức từ:
$$\boxed{F = BIl\sin 90° = BIl}$$
Đây là trường hợp lực từ CỰC ĐẠI
Giải thích: Khi dây vuông góc với từ trường, mọi đoạn dây đều chịu tác dụng lực tối đa.
b) Dây dẫn song song với từ trường (α = 0° hoặc 180°):
Khi dây dẫn song song với các đường sức từ:
$$\boxed{F = BIl\sin 0° = 0}$$
KHÔNG có lực từ tác dụng
Giải thích: Dòng điện chạy dọc theo đường sức từ nên không bị lực từ tác dụng.
c) Dây dẫn nghiêng góc α:
Trường hợp tổng quát:
$$F = BIl\sin\alpha$$
với $0° < \alpha < 90°$
3. Quy tắc bàn tay trái (xác định chiều lực)
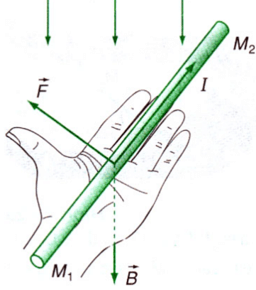
Quy tắc bàn tay trái giúp xác định chiều của lực từ:
Cách thực hiện:
- Đưa bàn tay trái ra, duỗi thẳng các ngón
- Đặt bàn tay sao cho:
- Chiều từ cổ tay đến ngón tay: hướng của vector cảm ứng từ $\vec{B}$ (từ cực Bắc sang cực Nam)
- Bốn ngón thẳng: hướng của dòng điện $\vec{I}$ (chiều dòng điện quy ước)
- Ngón cái choãi ra 90°: chỉ hướng của lực từ $\vec{F}$
Lưu ý quan trọng:
- $\vec{B}$, $\vec{I}$, $\vec{F}$ tạo thành một hệ ba vector vuông góc với nhau
- Lực từ luôn vuông góc với mặt phẳng chứa dòng điện và từ trường
4. Ví dụ minh họa
Ví dụ 1: Tính lực từ cơ bản
Đề bài: Một dây dẫn thẳng dài 50 cm mang dòng điện I = 4A, đặt vuông góc trong từ trường đều có cảm ứng từ B = 0.5T. Tính lực từ tác dụng lên dây dẫn.
Lời giải:
Bước 1: Đổi đơn vị
- l = 50 cm = 0.5 m
Bước 2: Xác định góc
- Dây vuông góc với $\vec{B}$ → α = 90°
Bước 3: Áp dụng công thức $$F = BIl\sin 90° = BIl$$ $$F = 0.5 \times 4 \times 0.5 = 1 \text{ N}$$
Kết luận: Lực từ tác dụng lên dây dẫn là 1 N.
Ví dụ 2: Dây dẫn nghiêng
Đề bài: Dây dẫn như ví dụ 1 nhưng hợp với vector cảm ứng từ $\vec{B}$ một góc 30°. Tính lực từ tác dụng lên dây.
Lời giải:
Bước 1: Áp dụng công thức với góc α = 30° $$F = BIl\sin 30°$$ $$F = 0.5 \times 4 \times 0.5 \times \sin 30°$$ $$F = 1 \times 0.5 = 0.5 \text{ N}$$
Kết luận: Lực từ giảm xuống còn 0.5 N (bằng một nửa so với trường hợp vuông góc).
Ví dụ 3: Tìm cường độ dòng điện
Đề bài: Dây dẫn dài 40 cm đặt vuông góc trong từ trường B = 0.2T. Lực từ tác dụng lên dây là 0.4 N. Tính cường độ dòng điện.
Lời giải:
Bước 1: Từ công thức $F = BIl$ $$I = \frac{F}{Bl}$$
Bước 2: Thay số $$I = \frac{0.4}{0.2 \times 0.4} = \frac{0.4}{0.08} = 5 \text{ A}$$
Kết luận: Cường độ dòng điện là 5 A.
5. Ứng dụng: Động cơ điện
Nguyên lý hoạt động:
Động cơ điện hoạt động dựa trên lực từ tác dụng lên khung dây có dòng điện trong từ trường.
Cấu tạo:
- Khung dây có N vòng, diện tích S
- Đặt trong từ trường B
- Có dòng điện I chạy qua
Mô men lực tác dụng lên khung dây:
$$\boxed{M = NBIS\sin\alpha}$$
Trong đó:
- $M$: mô men lực (N.m)
- $N$: số vòng dây
- $B$: cảm ứng từ (T)
- $I$: cường độ dòng điện (A)
- $S$: diện tích khung (m²)
- $\alpha$: góc giữa pháp tuyến khung và $\vec{B}$
Mô men cực đại: $$M_{max} = NBIS$$ (khi α = 90°, tức khung song song với $\vec{B}$)
Ví dụ 4: Khung dây chữ nhật có 100 vòng, diện tích 0.04 m², dòng điện 2A, đặt trong từ trường B = 0.5T. Khung đặt sao cho pháp tuyến hợp với $\vec{B}$ góc 90°. Tính mô men lực.
Lời giải: $$M = NBIS\sin 90° = 100 \times 0.5 \times 2 \times 0.04 \times 1 = 4 \text{ N.m}$$
III. LỰC LORENTZ (Lực từ tác dụng lên hạt mang điện)
1. Định nghĩa lực Lorentz
Định nghĩa: Lực Lorentz là lực từ tác dụng lên một hạt mang điện q chuyển động với vận tốc $\vec{v}$ trong từ trường $\vec{B}$.
Công thức lực Lorentz:
$$\boxed{F_L = |q|vB\sin\alpha}$$
Trong đó:
- $F_L$: lực Lorentz (đơn vị: N – Newton)
- $q$: điện tích của hạt (đơn vị: C – Coulomb)
- $v$: vận tốc của hạt (đơn vị: m/s)
- $B$: cảm ứng từ (đơn vị: T – Tesla)
- $\alpha$: góc giữa vector vận tốc $\vec{v}$ và vector cảm ứng từ $\vec{B}$
Dạng vector: $$\vec{F_L} = q(\vec{v} \times \vec{B})$$
Lưu ý quan trọng:
- Dấu giá trị tuyệt đối $|q|$ đảm bảo độ lớn lực luôn dương
- Chiều lực phụ thuộc vào dấu của điện tích
2. Các trường hợp đặc biệt
a) Hạt chuyển động vuông góc với từ trường (α = 90°):
$$\boxed{F_L = |q|vB}$$
Lực CỰC ĐẠI → Hạt chuyển động tròn đều
Giải thích: Lực Lorentz đóng vai trò lực hướng tâm, kéo hạt chuyển động theo quỹ đạo tròn.
b) Hạt chuyển động song song với từ trường (α = 0° hoặc 180°):
$$\boxed{F_L = 0}$$
KHÔNG có lực Lorentz → Hạt chuyển động thẳng đều
Giải thích: Vận tốc song song với từ trường nên không có lực tác dụng.
3. Quy tắc bàn tay trái cho lực Lorentz
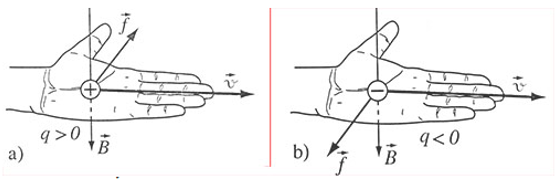
Áp dụng cho hạt mang điện tích dương (q > 0):
- Đưa bàn tay trái ra, duỗi thẳng
- Đặt bàn tay sao cho:
- Chiều từ cổ tay đến ngón tay: hướng của $\vec{B}$
- Bốn ngón: hướng của $\vec{v}$ (vận tốc hạt)
- Ngón cái: hướng của $\vec{F_L}$ (lực Lorentz)
Với hạt mang điện tích âm (q < 0):
- Áp dụng quy tắc bàn tay trái như trên
- Sau đó đảo ngược chiều lực (lấy chiều ngược lại)
Ví dụ:
- Electron (e⁻): Lực ngược với chiều xác định bởi quy tắc bàn tay trái
- Proton (p⁺): Lực cùng chiều với quy tắc bàn tay trái
4. Chuyển động của hạt điện trong từ trường
a) Chuyển động tròn đều (v ⊥ B):
Khi hạt chuyển động vuông góc với từ trường, lực Lorentz đóng vai trò lực hướng tâm:
$$|q|vB = \frac{mv^2}{r}$$
Bán kính quỹ đạo tròn:
$$\boxed{r = \frac{mv}{|q|B}}$$
Chu kỳ chuyển động:
$$\boxed{T = \frac{2\pi r}{v} = \frac{2\pi m}{|q|B}}$$
Tần số chuyển động:
$$\boxed{f = \frac{1}{T} = \frac{|q|B}{2\pi m}}$$
Tốc độ góc:
$$\omega = \frac{2\pi}{T} = \frac{|q|B}{m}$$
Lưu ý CỰC KỲ QUAN TRỌNG:
- Chu kỳ T và tần số f KHÔNG phụ thuộc vào vận tốc v!
- Chỉ phụ thuộc vào: điện tích q, khối lượng m, cảm ứng từ B
- Đây là nguyên lý hoạt động của máy gia tốc cyclotron
b) Chuyển động xoắn ốc (v không vuông góc B):
Khi vận tốc hợp với từ trường một góc α ≠ 90°, ta phân tích vận tốc thành hai thành phần:
Phân tích vận tốc: $$\vec{v} = \vec{v}_{//} + \vec{v}_{\perp}$$
- $\vec{v}_{//} = v\cos\alpha$: thành phần song song với $\vec{B}$
- $\vec{v}_{\perp} = v\sin\alpha$: thành phần vuông góc với $\vec{B}$
Chuyển động tổng hợp:
- Thành phần song song: Chuyển động thẳng đều (không chịu lực)
- Thành phần vuông góc: Chuyển động tròn đều (chịu lực hướng tâm)
- Kết quả: Quỹ đạo xoắn ốc (helix)
Bán kính xoắn ốc: $$r = \frac{mv_{\perp}}{|q|B} = \frac{mv\sin\alpha}{|q|B}$$
Bước xoắn (khoảng cách giữa hai vòng liên tiếp): $$h = v_{//} \cdot T = v\cos\alpha \cdot \frac{2\pi m}{|q|B}$$
5. Ví dụ minh họa về lực Lorentz
Ví dụ 5: Tính lực Lorentz cơ bản
Đề bài: Một electron (điện tích $e = -1.6 \times 10^{-19}$ C, khối lượng $m_e = 9.1 \times 10^{-31}$ kg) chuyển động vuông góc với từ trường B = 0.2T với vận tốc v = 10⁶ m/s. Tính: a) Lực Lorentz tác dụng lên electron b) Bán kính quỹ đạo chuyển động
Lời giải:
Câu a) Lực Lorentz: $$F_L = |e|vB\sin 90° = |e|vB$$ $$F_L = 1.6 \times 10^{-19} \times 10^6 \times 0.2$$ $$F_L = 3.2 \times 10^{-14} \text{ N}$$
Câu b) Bán kính quỹ đạo: $$r = \frac{m_e v}{|e|B}$$ $$r = \frac{9.1 \times 10^{-31} \times 10^6}{1.6 \times 10^{-19} \times 0.2}$$ $$r = \frac{9.1 \times 10^{-25}}{3.2 \times 10^{-20}}$$ $$r = 2.84 \times 10^{-5} \text{ m} = 28.4 , \mu\text{m}$$
Kết luận:
- Lực Lorentz: $3.2 \times 10^{-14}$ N
- Bán kính quỹ đạo: 28.4 μm
Ví dụ 6: Chu kỳ và tần số
Đề bài: Một proton (khối lượng $m_p = 1.67 \times 10^{-27}$ kg, điện tích $e = 1.6 \times 10^{-19}$ C) chuyển động trong từ trường B = 0.5T theo quỹ đạo tròn. Tính: a) Chu kỳ chuyển động b) Tần số chuyển động
Lời giải:
Câu a) Chu kỳ: $$T = \frac{2\pi m_p}{eB}$$ $$T = \frac{2\pi \times 1.67 \times 10^{-27}}{1.6 \times 10^{-19} \times 0.5}$$ $$T = \frac{10.49 \times 10^{-27}}{8 \times 10^{-20}}$$ $$T = 1.31 \times 10^{-7} \text{ s} = 131 \text{ ns}$$
Câu b) Tần số: $$f = \frac{1}{T} = \frac{1}{1.31 \times 10^{-7}}$$ $$f = 7.63 \times 10^6 \text{ Hz} = 7.63 \text{ MHz}$$
Kết luận:
- Chu kỳ: 131 ns
- Tần số: 7.63 MHz
Lưu ý: Chu kỳ và tần số không phụ thuộc vào vận tốc!
Ví dụ 7: Bài toán ngược – Tìm vận tốc
Đề bài: Một hạt alpha (điện tích $q = 2e = 3.2 \times 10^{-19}$ C, khối lượng $m = 6.64 \times 10^{-27}$ kg) chuyển động vuông góc trong từ trường B = 0.4T theo quỹ đạo tròn bán kính r = 10 cm. Tính vận tốc của hạt.
Lời giải:
Từ công thức bán kính: $$r = \frac{mv}{qB}$$
Suy ra: $$v = \frac{qBr}{m}$$
Thay số: $$v = \frac{3.2 \times 10^{-19} \times 0.4 \times 0.1}{6.64 \times 10^{-27}}$$ $$v = \frac{1.28 \times 10^{-20}}{6.64 \times 10^{-27}}$$ $$v = 1.93 \times 10^6 \text{ m/s}$$
Kết luận: Vận tốc hạt alpha là $1.93 \times 10^6$ m/s.
IV. SO SÁNH LỰC TỪ VÀ LỰC LORENTZ
Bảng so sánh chi tiết
| Tiêu chí | Lực từ (dây dẫn) | Lực Lorentz (hạt điện) |
|---|---|---|
| Đối tượng tác dụng | Dây dẫn có dòng điện | Hạt mang điện chuyển động |
| Công thức | $F = BIl\sin\alpha$ | $F_L = |q|vB\sin\alpha$ |
| Đại lượng đặc trưng | I (dòng điện), l (chiều dài) | q (điện tích), v (vận tốc) |
| Đơn vị đại lượng | A, m | C, m/s |
| Chiều lực | Quy tắc bàn tay trái | Quy tắc bàn tay trái (q>0), ngược lại (q<0) |
| Ứng dụng chính | Động cơ điện, loa, micro | Máy gia tốc hạt, màn hình CRT |
| Quỹ đạo | Dây cố định, bị kéo/đẩy | Hạt chuyển động tròn hoặc xoắn |
| Công sinh ra | Có thể sinh công | Không sinh công (lực ⊥ v) |
Mối liên hệ giữa hai loại lực
Dòng điện là dòng hạt mang điện:
Dòng điện I trong dây dẫn thực chất là dòng các hạt mang điện chuyển động:
$$I = \frac{q}{t}$$
Trong đó q là điện tích chuyển qua tiết diện trong thời gian t.
Suy ra mối liên hệ:
$$F = BIl = B \cdot \frac{q}{t} \cdot l = Bq \cdot \frac{l}{t} = Bqv$$
Kết luận:
- Lực từ trên dây dẫn = Tổng các lực Lorentz tác dụng lên các hạt điện tự do trong dây!
- $F_{dây} = \sum F_L$
Ý nghĩa: Hai công thức về bản chất là một, chỉ khác cách nhìn:
- Nhìn ở cấp độ vĩ mô → Lực từ tác dụng lên dây
- Nhìn ở cấp độ vi mô → Lực Lorentz tác dụng lên từng hạt
V. BẢNG CÔNG THỨC TỔNG HỢP
A. Lực từ tác dụng lên dây dẫn
| Trường hợp | Công thức | Điều kiện | Ghi chú |
|---|---|---|---|
| Tổng quát | $F = BIl\sin\alpha$ | Góc α bất kỳ | α: góc giữa dây và $\vec{B}$ |
| Vuông góc | $F = BIl$ | $\alpha = 90°$ | Lực cực đại |
| Song song | $F = 0$ | $\alpha = 0°$ hoặc $180°$ | Không có lực |
| Khung dây | $M = NBIS\sin\alpha$ | Mô men lực | N vòng, diện tích S |
B. Lực Lorentz tác dụng lên hạt điện
| Trường hợp | Công thức | Điều kiện | Ghi chú |
|---|---|---|---|
| Tổng quát | $F_L = |q|vB\sin\alpha$ | Góc α bất kỳ | α: góc giữa $\vec{v}$ và $\vec{B}$ |
| Vuông góc | $F_L = |q|vB$ | $\alpha = 90°$ | Chuyển động tròn |
| Song song | $F_L = 0$ | $\alpha = 0°$ hoặc $180°$ | Chuyển động thẳng |
C. Chuyển động tròn của hạt điện (v ⊥ B)
| Đại lượng | Công thức | Ý nghĩa |
|---|---|---|
| Bán kính quỹ đạo | $r = \frac{mv}{|q|B}$ | Phụ thuộc v |
| Chu kỳ | $T = \frac{2\pi m}{|q|B}$ | Không phụ thuộc v |
| Tần số | $f = \frac{|q|B}{2\pi m}$ | Không phụ thuộc v |
| Tốc độ góc | $\omega = \frac{|q|B}{m}$ | Không phụ thuộc v |
| Lực hướng tâm | $F = |q|vB = \frac{mv^2}{r}$ | Lực Lorentz = Lực hướng tâm |
D. Quy tắc bàn tay trái
Xác định chiều lực từ:
| Bộ phận bàn tay | Dây dẫn có dòng điện | Hạt mang điện (q > 0) |
|---|---|---|
| Từ cổ tay → ngón tay | Hướng của $\vec{B}$ | Hướng của $\vec{B}$ |
| Bốn ngón thẳng | Chiều dòng điện $\vec{I}$ | Chiều vận tốc $\vec{v}$ |
| Ngón cái choãi 90° | Chiều lực từ $\vec{F}$ | Chiều lực $\vec{F_L}$ |
Lưu ý: Với hạt mang điện âm (q < 0), lực có chiều ngược lại.
E. Đơn vị đo
| Đại lượng | Ký hiệu | Đơn vị | Quy đổi |
|---|---|---|---|
| Lực từ | F, $F_L$ | N (Newton) | |
| Cảm ứng từ | B | T (Tesla) | 1 T = 1 Wb/m² |
| Dòng điện | I | A (Ampere) | |
| Chiều dài | l | m (mét) | 1 m = 100 cm |
| Điện tích | q | C (Coulomb) | $e = 1.6 \times 10^{-19}$ C |
| Vận tốc | v | m/s | |
| Khối lượng | m | kg | $m_e = 9.1 \times 10^{-31}$ kg |
VI. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Dạng chung của lực từ:
“B nhân (cái gì chuyển động) nhân (độ dài/vận tốc) nhân sin α”
- Dây dẫn: $F = B \times I \times l \times \sin\alpha$
- Hạt điện: $F_L = B \times q \times v \times \sin\alpha$
Lực cực đại khi vuông góc:
α = 90° → sin α = 1 → Lực đạt giá trị lớn nhất
Không có lực khi song song:
α = 0° hoặc 180° → sin α = 0 → Lực bằng 0
Chu kỳ không phụ thuộc vận tốc:
$$T = \frac{2\pi m}{|q|B}$$
Không có v trong công thức!
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm góc α
Sai: Lấy góc giữa dây/vận tốc và mặt phẳng vuông góc với $\vec{B}$ ❌
Đúng: α là góc giữa dây/vận tốc và chính vector $\vec{B}$ ✓
❌ SAI LẦM 2: Quên lấy trị tuyệt đối |q|
Sai: $F_L = qvB$ (có thể âm) ❌
Đúng: $F_L = |q|vB$ (luôn dương) ✓
Độ lớn lực luôn dương, dấu của q chỉ ảnh hưởng đến chiều lực.
❌ SAI LẦM 3: Nhầm công thức dây dẫn với hạt điện
Sai:
- Dây dẫn: $F = qvB$ ❌
- Hạt điện: $F_L = BIl$ ❌
Đúng:
- Dây dẫn: $F = BIl\sin\alpha$ ✓
- Hạt điện: $F_L = |q|vB\sin\alpha$ ✓
❌ SAI LẦM 4: Quên đổi đơn vị
Sai: l = 50 cm (dùng luôn) ❌
Đúng: l = 50 cm = 0.5 m ✓
Lưu ý: Luôn đổi về đơn vị chuẩn: m, A, T, C, m/s
❌ SAI LẦM 5: Dùng sai quy tắc bàn tay trái cho điện tích âm
Sai: Áp dụng quy tắc bàn tay trái trực tiếp cho electron ❌
Đúng: Áp dụng quy tắc cho điện tích dương, sau đó đảo ngược chiều lực ✓
3. Lưu ý đặc biệt
Về điện tích âm (electron):
- Electron có điện tích $e = -1.6 \times 10^{-19}$ C
- Trong công thức, dùng $|e| = 1.6 \times 10^{-19}$ C
- Chiều lực ngược với quy tắc bàn tay trái
Về chu kỳ và tần số:
- $T = \frac{2\pi m}{|q|B}$ KHÔNG phụ thuộc vận tốc v
- Mọi hạt cùng loại (cùng q, m) trong cùng từ trường B có cùng chu kỳ T
- Đây là nguyên lý của máy gia tốc cyclotron
Về bán kính quỹ đạo:
- $r = \frac{mv}{|q|B}$ phụ thuộc vào vận tốc v
- Hạt có động năng lớn → v lớn → r lớn
- Hạt nặng hơn → m lớn → r lớn
VII. BÀI TẬP MẪU
Dạng 1: Lực từ tác dụng lên dây dẫn
Đề bài: Một dây dẫn thẳng dài 80 cm mang dòng điện I = 5A, đặt trong từ trường đều có cảm ứng từ B = 0.4T. Dây dẫn hợp với vector cảm ứng từ một góc 30°. Tính lực từ tác dụng lên dây dẫn.
Lời giải:
Bước 1: Đổi đơn vị
- l = 80 cm = 0.8 m
Bước 2: Áp dụng công thức $$F = BIl\sin\alpha$$ $$F = 0.4 \times 5 \times 0.8 \times \sin 30°$$ $$F = 0.4 \times 5 \times 0.8 \times 0.5$$ $$F = 0.8 \text{ N}$$
Kết luận: Lực từ tác dụng lên dây dẫn là 0.8 N.
Dạng 2: Lực Lorentz
Đề bài: Một hạt alpha (điện tích $q = 2e = 3.2 \times 10^{-19}$ C) chuyển động vuông góc với từ trường B = 0.5T với vận tốc v = $2 \times 10^5$ m/s. Tính lực Lorentz tác dụng lên hạt.
Lời giải:
$$F_L = |q|vB\sin 90° = |q|vB$$ $$F_L = 3.2 \times 10^{-19} \times 2 \times 10^5 \times 0.5$$ $$F_L = 3.2 \times 10^{-14} \text{ N}$$
Kết luận: Lực Lorentz là $3.2 \times 10^{-14}$ N.
Dạng 3: Bán kính quỹ đạo
Đề bài: Một electron (khối lượng $m_e = 9.1 \times 10^{-31}$ kg, điện tích $|e| = 1.6 \times 10^{-19}$ C) chuyển động vuông góc trong từ trường B = $10^{-3}$ T với vận tốc v = $10^7$ m/s. Tính bán kính quỹ đạo chuyển động.
Lời giải:
$$r = \frac{m_e v}{|e|B}$$ $$r = \frac{9.1 \times 10^{-31} \times 10^7}{1.6 \times 10^{-19} \times 10^{-3}}$$ $$r = \frac{9.1 \times 10^{-24}}{1.6 \times 10^{-22}}$$ $$r = 5.69 \times 10^{-2} \text{ m} = 5.69 \text{ cm}$$
Kết luận: Bán kính quỹ đạo là 5.69 cm.
Dạng 4: Chu kỳ và tần số
Đề bài: Một proton (khối lượng $m_p = 1.67 \times 10^{-27}$ kg, điện tích $e = 1.6 \times 10^{-19}$ C) chuyển động trong từ trường B = 0.2T. Tính: a) Chu kỳ chuyển động b) Tần số chuyển động
Lời giải:
Câu a) Chu kỳ: $$T = \frac{2\pi m_p}{eB}$$ $$T = \frac{2\pi \times 1.67 \times 10^{-27}}{1.6 \times 10^{-19} \times 0.2}$$ $$T = \frac{10.49 \times 10^{-27}}{3.2 \times 10^{-20}}$$ $$T = 3.28 \times 10^{-7} \text{ s} = 328 \text{ ns}$$
Câu b) Tần số: $$f = \frac{1}{T} = \frac{1}{3.28 \times 10^{-7}}$$ $$f = 3.05 \times 10^6 \text{ Hz} = 3.05 \text{ MHz}$$
Kết luận:
- Chu kỳ: 328 ns
- Tần số: 3.05 MHz
Dạng 5: Mô men lực trong động cơ điện
Đề bài: Một khung dây chữ nhật gồm 100 vòng, diện tích mỗi vòng S = 0.05 m², mang dòng điện I = 2A, đặt trong từ trường đều B = 0.4T. Khung đặt sao cho pháp tuyến của khung vuông góc với vector cảm ứng từ. Tính mô men lực tác dụng lên khung.
Lời giải:
Phân tích: Pháp tuyến vuông góc với $\vec{B}$ → Mặt phẳng khung song song với $\vec{B}$ → α = 90°
$$M = NBIS\sin 90° = NBIS$$ $$M = 100 \times 0.4 \times 2 \times 0.05 \times 1$$ $$M = 4 \text{ N.m}$$
Kết luận: Mô men lực tác dụng lên khung là 4 N.m.
VIII. KẾT LUẬN
Bài viết đã trình bày đầy đủ kiến thức về lực từ và lực Lorentz:
Lực từ tác dụng lên dây dẫn:
- Công thức: $F = BIl\sin\alpha$
- Ứng dụng: Động cơ điện, loa, micro
- Quy tắc bàn tay trái xác định chiều lực
Lực Lorentz tác dụng lên hạt điện:
- Công thức: $F_L = |q|vB\sin\alpha$
- Chuyển động tròn: $r = \frac{mv}{|q|B}$, $T = \frac{2\pi m}{|q|B}$
- Ứng dụng: Máy gia tốc hạt, màn hình CRT
Mối liên hệ:
- Lực từ trên dây = Tổng lực Lorentz trên các hạt
- Cùng bản chất, khác cách nhìn (vĩ mô vs vi mô)
Lời khuyên học tập
📌 Học thuộc hai công thức chính – Nền tảng của mọi bài toán
📌 Phân biệt rõ hai loại lực:
- Dây dẫn → dùng I và l
- Hạt điện → dùng q và v
📌 Luyện quy tắc bàn tay trái – Vẽ hình, thực hành nhiều lần
📌 Nhớ: Chu kỳ không phụ thuộc v – Điều đặc biệt về chuyển động tròn
📌 Chú ý điện tích âm – Đảo ngược chiều lực
📌 Đổi đơn vị cẩn thận – Luôn về m, A, T, C

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
