Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ KHỐI TRÒN XOAY
- 1. Khối tròn xoay là gì?
- 2. Các khối tròn xoay cơ bản
- II. CÔNG THỨC TỔNG QUÁT TÍNH THỂ TÍCH KHỐI TRÒN XOAY
- A. Quay quanh trục Ox
- B. Quay quanh trục Oy
- C. Công thức khi có hai đường cong
- III. CÔNG THỨC CHO CÁC KHỐI TRÒN XOAY CƠ BẢN
- A. Hình trụ (Cylinder)
- B. Hình nón (Cone)
- C. Hình cầu (Sphere)
- D. Hình nón cụt (Truncated Cone)
- E. Hình xuyến (Torus)
- IV. PHƯƠNG PHÁP GIẢI BÀI TẬP TÍCH PHÂN
- Bước 1: Vẽ hình và xác định miền
- Bước 2: Xác định cận tích phân
- Bước 3: Chọn công thức phù hợp
- Bước 4: Tính tích phân
- Bước 5: Kết luận
- V. CÁC DẠNG BÀI TẬP THƯỜNG GẶP
- VI. MẸO VÀ LƯU Ý
- 1. Các sai lầm thường gặp
- 2. Mẹo tính nhanh
- 3. Công thức nguyên hàm thường dùng
- VII. KẾT LUẬN
- Tổng kết
I. GIỚI THIỆU VỀ KHỐI TRÒN XOAY
1. Khối tròn xoay là gì?
Định nghĩa: Khối tròn xoay là khối hình học được tạo ra khi quay một hình phẳng quanh một đường thẳng cố định (gọi là trục quay).
Trục quay:
- Thường là trục hoành Ox hoặc trục tung Oy
- Có thể là bất kỳ đường thẳng nào trong mặt phẳng
- Hình phẳng quay 360° quanh trục tạo thành khối tròn xoay
Nguyên lý tạo thành:
- Mỗi điểm của hình phẳng vạch ra một đường tròn
- Tập hợp tất cả các đường tròn tạo thành bề mặt khối tròn xoay
- Khối tròn xoay có tính đối xứng quanh trục
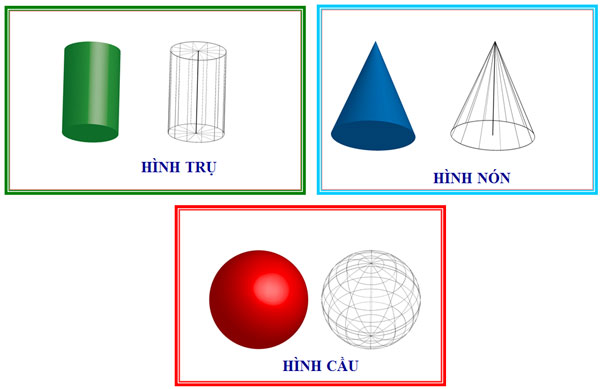
2. Các khối tròn xoay cơ bản
Hình trụ (Cylinder):
- Tạo bởi: Quay hình chữ nhật quanh một cạnh
- Đặc điểm: Hai đáy là hai hình tròn bằng nhau và song song
- Ví dụ thực tế: Lon nước, ống dẫn, trụ cột
Hình nón (Cone):
- Tạo bởi: Quay tam giác vuông quanh một cạnh góc vuông
- Đặc điểm: Có đáy hình tròn và đỉnh
- Ví dụ thực tế: Nón lá, phễu, cột mốc
Hình cầu (Sphere):
- Tạo bởi: Quay nửa hình tròn quanh đường kính
- Đặc điểm: Mọi điểm trên mặt cầu cách đều tâm
- Ví dụ thực tế: Quả bóng, trái đất, mặt trời
Khối tròn xoay bất kỳ:
- Tạo bởi: Quay đường cong $y = f(x)$ quanh trục
- Đặc điểm: Hình dạng phức tạp, cần dùng tích phân
- Ví dụ: Bình hoa, chai lọ, đồ gốm
II. CÔNG THỨC TỔNG QUÁT TÍNH THỂ TÍCH KHỐI TRÒN XOAY
A. Quay quanh trục Ox
Điều kiện:
Cho hàm số $y = f(x)$ liên tục và không âm trên đoạn $[a, b]$.
Miền quay:
Hình phẳng giới hạn bởi:
- Đường cong $y = f(x)$
- Trục hoành Ox
- Hai đường thẳng $x = a$ và $x = b$
Công thức:
$$\boxed{V = \pi \int_{a}^{b} f^2(x) , dx = \pi \int_{a}^{b} y^2 , dx}$$
Cách nhớ: “Pi nhân tích phân y bình phương dx”
Giải thích:
- Mỗi tiết diện vuông góc với trục Ox là hình tròn bán kính $y = f(x)$
- Diện tích tiết diện: $S(x) = \pi y^2 = \pi [f(x)]^2$
- Tích phân từ $a$ đến $b$ để tính thể tích tổng
Ví dụ 1: Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi $y = x$, trục Ox, $x = 0$ và $x = 2$ quanh trục Ox.
Lời giải:
Bước 1: Xác định hàm số và cận:
- $f(x) = x$
- Cận: $a = 0$, $b = 2$
Bước 2: Áp dụng công thức: $$V = \pi \int_{0}^{2} x^2 , dx$$
Bước 3: Tính tích phân: $$V = \pi \left[ \frac{x^3}{3} \right]_{0}^{2} = \pi \left( \frac{8}{3} – 0 \right) = \frac{8\pi}{3}$$
Kết luận: Thể tích là $\frac{8\pi}{3}$ đơn vị khối $\approx 8.38$ đơn vị khối.
B. Quay quanh trục Oy
Điều kiện:
Cho hàm số $x = g(y)$ liên tục và không âm trên đoạn $[c, d]$.
Miền quay:
Hình phẳng giới hạn bởi:
- Đường cong $x = g(y)$
- Trục tung Oy
- Hai đường thẳng $y = c$ và $y = d$
Công thức:
$$\boxed{V = \pi \int_{c}^{d} g^2(y) , dy = \pi \int_{c}^{d} x^2 , dy}$$
Lưu ý:
- Cần viết hàm số dưới dạng $x = g(y)$
- Biến tích phân là $dy$, không phải $dx$
- Cận tích phân là giá trị của $y$
Ví dụ 2: Tính thể tích khối tròn xoay khi quay đường cong $x = y^2$ từ $y = 0$ đến $y = 2$ quanh trục Oy.
Lời giải:
Bước 1: Xác định:
- $g(y) = y^2$
- Cận: $c = 0$, $d = 2$
Bước 2: Áp dụng công thức: $$V = \pi \int_{0}^{2} (y^2)^2 , dy = \pi \int_{0}^{2} y^4 , dy$$
Bước 3: Tính tích phân: $$V = \pi \left[ \frac{y^5}{5} \right]_{0}^{2} = \pi \cdot \frac{32}{5} = \frac{32\pi}{5}$$
Kết luận: Thể tích là $\frac{32\pi}{5}$ đơn vị khối $\approx 20.11$ đơn vị khối.
C. Công thức khi có hai đường cong
Điều kiện:
Hình phẳng giới hạn bởi:
- Hai đường cong $y = f(x)$ và $y = g(x)$ với $f(x) \geq g(x) \geq 0$ trên $[a, b]$
- Hai đường thẳng $x = a$ và $x = b$
- Quay quanh trục Ox
Công thức:
$$\boxed{V = \pi \int_{a}^{b} [f^2(x) – g^2(x)] , dx}$$
Cách nhớ: “Bình phương lớn trừ bình phương nhỏ, nhân pi”
Giải thích:
- Thể tích = Thể tích khối ngoài – Thể tích khối trong
- $f(x)$ là đường cong phía ngoài (xa trục hơn)
- $g(x)$ là đường cong phía trong (gần trục hơn)
Ví dụ 3: Tính thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi $y = x$ và $y = x^2$ quanh trục Ox.
Lời giải:
Bước 1: Tìm giao điểm: $$x = x^2 \Rightarrow x^2 – x = 0 \Rightarrow x(x-1) = 0$$ $$x = 0 \text{ hoặc } x = 1$$
Bước 2: Xác định đường nào lớn hơn trên $[0, 1]$:
- Thử $x = 0.5$: $f(0.5) = 0.5$, $g(0.5) = 0.25$
- Vậy $x \geq x^2$ trên $[0, 1]$
Bước 3: Áp dụng công thức: $$V = \pi \int_{0}^{1} (x^2 – x^4) , dx$$
Bước 4: Tính tích phân: $$V = \pi \left[ \frac{x^3}{3} – \frac{x^5}{5} \right]_{0}^{1} = \pi \left( \frac{1}{3} – \frac{1}{5} \right) = \pi \cdot \frac{2}{15} = \frac{2\pi}{15}$$
Kết luận: Thể tích là $\frac{2\pi}{15}$ đơn vị khối $\approx 0.419$ đơn vị khối.
III. CÔNG THỨC CHO CÁC KHỐI TRÒN XOAY CƠ BẢN
A. Hình trụ (Cylinder)
Định nghĩa:
Hình trụ được tạo ra khi quay hình chữ nhật quanh một trong các cạnh của nó.
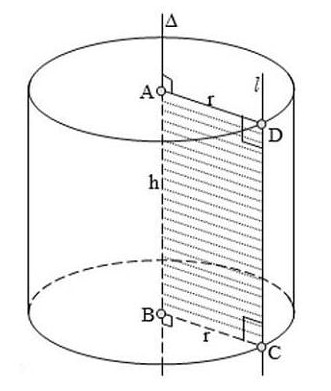
Công thức thể tích:
$$\boxed{V = \pi r^2 h}$$
Trong đó:
- $r$: bán kính đáy (bán kính hình tròn)
- $h$: chiều cao (khoảng cách giữa hai đáy)
Các công thức liên quan:
Diện tích xung quanh: $$S_{xq} = 2\pi rh$$
Diện tích toàn phần: $$S_{tp} = 2\pi r(r + h) = 2\pi r^2 + 2\pi rh$$
Ví dụ 4: Hình trụ có bán kính đáy $r = 3$ cm và chiều cao $h = 5$ cm. Tính thể tích và diện tích toàn phần.
Lời giải:
Thể tích: $$V = \pi \cdot 3^2 \cdot 5 = 45\pi \text{ cm}^3 \approx 141.37 \text{ cm}^3$$
Diện tích toàn phần: $$S_{tp} = 2\pi \cdot 3(3 + 5) = 48\pi \text{ cm}^2 \approx 150.80 \text{ cm}^2$$
Cách tạo từ tích phân: Quay hình chữ nhật có chiều cao $r$ (song song Oy) và chiều dài $h$ (từ $x = 0$ đến $x = h$) quanh Ox: $$V = \pi \int_{0}^{h} r^2 , dx = \pi r^2 h$$
B. Hình nón (Cone)
Định nghĩa:
Hình nón được tạo ra khi quay tam giác vuông quanh một cạnh góc vuông.
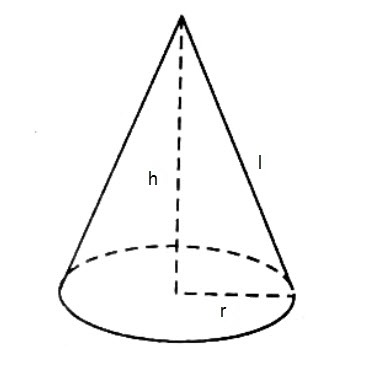
Công thức thể tích:
$$\boxed{V = \frac{1}{3}\pi r^2 h}$$
Trong đó:
- $r$: bán kính đáy
- $h$: chiều cao (từ đáy đến đỉnh)
- $l = \sqrt{r^2 + h^2}$: đường sinh (độ dài cạnh bên)
Các công thức liên quan:
Diện tích xung quanh: $$S_{xq} = \pi rl$$
Diện tích toàn phần: $$S_{tp} = \pi r(r + l)$$
Quan hệ: $l^2 = r^2 + h^2$ (định lý Pythagore)
Ví dụ 5: Hình nón có bán kính đáy $r = 4$ cm và chiều cao $h = 3$ cm. Tính thể tích và đường sinh.
Lời giải:
Thể tích: $$V = \frac{1}{3}\pi \cdot 4^2 \cdot 3 = 16\pi \text{ cm}^3 \approx 50.27 \text{ cm}^3$$
Đường sinh: $$l = \sqrt{4^2 + 3^2} = \sqrt{16 + 9} = \sqrt{25} = 5 \text{ cm}$$
Cách tạo từ tích phân: Quay đường thẳng $y = \frac{r}{h}x$ từ $x = 0$ đến $x = h$ quanh trục Ox: $$V = \pi \int_{0}^{h} \left(\frac{r}{h}x\right)^2 dx = \pi \cdot \frac{r^2}{h^2} \int_{0}^{h} x^2 , dx$$ $$= \pi \cdot \frac{r^2}{h^2} \cdot \frac{h^3}{3} = \frac{1}{3}\pi r^2 h$$
C. Hình cầu (Sphere)
Định nghĩa:
Hình cầu được tạo ra khi quay nửa đường tròn quanh đường kính.
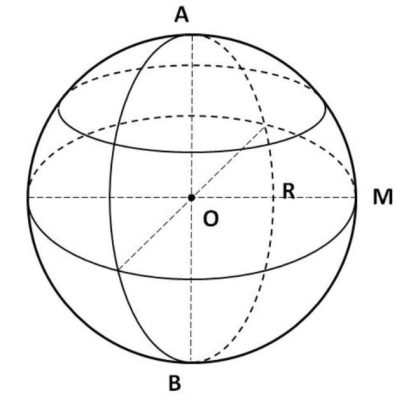
Công thức thể tích:
$$\boxed{V = \frac{4}{3}\pi R^3}$$
Trong đó: $R$ là bán kính hình cầu.
Diện tích mặt cầu:
$$S = 4\pi R^2$$
Ví dụ 6: Hình cầu có bán kính $R = 3$ cm. Tính thể tích và diện tích mặt cầu.
Lời giải:
Thể tích: $$V = \frac{4}{3}\pi \cdot 3^3 = \frac{4}{3}\pi \cdot 27 = 36\pi \text{ cm}^3 \approx 113.10 \text{ cm}^3$$
Diện tích mặt cầu: $$S = 4\pi \cdot 3^2 = 36\pi \text{ cm}^2 \approx 113.10 \text{ cm}^2$$
Cách tạo từ tích phân: Quay nửa đường tròn $y = \sqrt{R^2 – x^2}$ từ $x = -R$ đến $x = R$ quanh trục Ox: $$V = \pi \int_{-R}^{R} (\sqrt{R^2 – x^2})^2 , dx = \pi \int_{-R}^{R} (R^2 – x^2) , dx$$ $$= \pi \left[ R^2x – \frac{x^3}{3} \right]_{-R}^{R} = \pi \left[ 2R^3 – \frac{2R^3}{3} \right] = \frac{4}{3}\pi R^3$$
D. Hình nón cụt (Truncated Cone)
Định nghĩa:
Hình nón cụt là phần của hình nón bị cắt bởi một mặt phẳng song song với đáy.
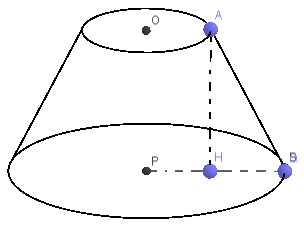
Công thức thể tích:
$$\boxed{V = \frac{1}{3}\pi h(R^2 + Rr + r^2)}$$
Trong đó:
- $R$: bán kính đáy lớn
- $r$: bán kính đáy nhỏ
- $h$: chiều cao (khoảng cách giữa hai đáy)
Cách nhớ: “Một phần ba pi h nhân ngoặc R bình cộng R nhân r cộng r bình”
Ví dụ 7: Hình nón cụt có bán kính đáy lớn $R = 5$ cm, bán kính đáy nhỏ $r = 3$ cm, chiều cao $h = 4$ cm. Tính thể tích.
Lời giải:
$$V = \frac{1}{3}\pi \cdot 4(5^2 + 5 \cdot 3 + 3^2)$$ $$= \frac{4\pi}{3}(25 + 15 + 9)$$ $$= \frac{4\pi}{3} \cdot 49 = \frac{196\pi}{3} \text{ cm}^3 \approx 205.25 \text{ cm}^3$$
Công thức thay thế: $$V = V_{\text{nón lớn}} – V_{\text{nón nhỏ}}$$
E. Hình xuyến (Torus)
Định nghĩa:
Hình xuyến được tạo ra khi quay một hình tròn quanh một trục nằm ngoài hình tròn đó (trục không cắt hình tròn).
Công thức thể tích:
$$\boxed{V = 2\pi^2 Rr^2}$$
Trong đó:
- $R$: khoảng cách từ tâm hình tròn đến trục quay
- $r$: bán kính hình tròn
Diện tích bề mặt: $$S = 4\pi^2 Rr$$
Ví dụ: Bánh donut có $R = 5$ cm, $r = 2$ cm. $$V = 2\pi^2 \cdot 5 \cdot 2^2 = 40\pi^2 \text{ cm}^3 \approx 394.78 \text{ cm}^3$$
IV. PHƯƠNG PHÁP GIẢI BÀI TẬP TÍCH PHÂN
Bước 1: Vẽ hình và xác định miền
Mục đích: Hình dung rõ ràng miền cần quay
Cách làm:
- Vẽ đồ thị hàm số $y = f(x)$ trên hệ trục tọa độ
- Đánh dấu miền cần quay (thường là miền giữa đồ thị và trục)
- Xác định trục quay (Ox hoặc Oy)
- Gạch chéo hoặc tô màu miền cần quay
Lưu ý: Hình vẽ giúp tránh nhầm lẫn về cận và vị trí miền quay.
Bước 2: Xác định cận tích phân
Phương pháp:
Nếu quay quanh Ox:
- Tìm giao điểm của đồ thị với trục Ox hoặc với các đường thẳng đứng
- Giải phương trình để tìm $a$ và $b$
Nếu quay quanh Oy:
- Viết hàm dưới dạng $x = g(y)$
- Tìm giao điểm để xác định $c$ và $d$
Ví dụ: Với $y = x^2$ và $y = 2x$: $$x^2 = 2x \Rightarrow x^2 – 2x = 0 \Rightarrow x(x-2) = 0$$ $$x = 0 \text{ hoặc } x = 2$$
Bước 3: Chọn công thức phù hợp
Quyết định dựa trên:
Một đường cong:
- Quay quanh Ox: $V = \pi \int_{a}^{b} y^2 , dx$
- Quay quanh Oy: $V = \pi \int_{c}^{d} x^2 , dy$
Hai đường cong:
- Quay quanh Ox: $V = \pi \int_{a}^{b} (y_1^2 – y_2^2) , dx$
- (với $y_1 \geq y_2 \geq 0$)
Bước 4: Tính tích phân
Các kỹ thuật:
Đa thức: Khai triển và tích phân từng số hạng $$\int (x^3 + 2x^2) , dx = \frac{x^4}{4} + \frac{2x^3}{3} + C$$
Phân tích: Đưa về dạng cơ bản $$\int (x-1)^2 , dx = \int (x^2 – 2x + 1) , dx$$
Công thức hạ bậc: Với hàm lượng giác $$\sin^2 x = \frac{1 – \cos 2x}{2}$$ $$\cos^2 x = \frac{1 + \cos 2x}{2}$$
Bước 5: Kết luận
Yêu cầu:
- Ghi rõ đơn vị: đơn vị khối (cm³, m³, dm³)
- Làm tròn kết quả nếu cần (thường 2 chữ số thập phân)
- Kiểm tra: Thể tích luôn dương
V. CÁC DẠNG BÀI TẬP THƯỜNG GẶP
Dạng 1: Quay hàm đa thức quanh Ox
Phương pháp: Áp dụng $V = \pi \int y^2 , dx$
Bài tập 1: Tính thể tích khối tròn xoay khi quay hàm $y = x^2$ từ $x = 0$ đến $x = 1$ quanh trục Ox.
Lời giải:
$$V = \pi \int_{0}^{1} (x^2)^2 , dx = \pi \int_{0}^{1} x^4 , dx$$ $$= \pi \left[ \frac{x^5}{5} \right]_{0}^{1} = \pi \cdot \frac{1}{5} = \frac{\pi}{5}$$
Kết luận: Thể tích là $\frac{\pi}{5}$ đơn vị khối.
Dạng 2: Quay hàm phân thức
Bài tập 2: Tính thể tích khi quay $y = \frac{1}{x}$ từ $x = 1$ đến $x = 2$ quanh trục Ox.
Lời giải:
$$V = \pi \int_{1}^{2} \left(\frac{1}{x}\right)^2 dx = \pi \int_{1}^{2} \frac{1}{x^2} , dx$$ $$= \pi \left[ -\frac{1}{x} \right]_{1}^{2} = \pi \left( -\frac{1}{2} – (-1) \right) = \pi \cdot \frac{1}{2} = \frac{\pi}{2}$$
Kết luận: Thể tích là $\frac{\pi}{2}$ đơn vị khối.
Dạng 3: Quay hàm lượng giác
Bài tập 3: Tính thể tích khi quay $y = \sin x$ từ $x = 0$ đến $x = \pi$ quanh trục Ox.
Lời giải:
$$V = \pi \int_{0}^{\pi} \sin^2 x , dx$$
Sử dụng công thức hạ bậc: $\sin^2 x = \frac{1 – \cos 2x}{2}$
$$V = \pi \int_{0}^{\pi} \frac{1 – \cos 2x}{2} , dx = \frac{\pi}{2} \int_{0}^{\pi} (1 – \cos 2x) , dx$$ $$= \frac{\pi}{2} \left[ x – \frac{\sin 2x}{2} \right]_{0}^{\pi}$$ $$= \frac{\pi}{2} \left[ \pi – 0 – (0 – 0) \right] = \frac{\pi^2}{2}$$
Kết luận: Thể tích là $\frac{\pi^2}{2}$ đơn vị khối $\approx 4.93$ đơn vị khối.
Dạng 4: Quay giữa hai đường cong
Bài tập 4: Tính thể tích khi quay hình phẳng giới hạn bởi $y = x$ và $y = \sqrt{x}$ quanh trục Ox.
Lời giải:
Bước 1: Tìm giao điểm: $$x = \sqrt{x} \Rightarrow x^2 = x \Rightarrow x^2 – x = 0 \Rightarrow x = 0 \text{ hoặc } x = 1$$
Bước 2: Xác định đường nào lớn hơn:
- Thử $x = 0.25$: $\sqrt{0.25} = 0.5$, $0.25 = 0.25$
- Vậy $\sqrt{x} \geq x$ trên $[0, 1]$
Bước 3: Tính thể tích: $$V = \pi \int_{0}^{1} [(\sqrt{x})^2 – x^2] , dx = \pi \int_{0}^{1} (x – x^2) , dx$$ $$= \pi \left[ \frac{x^2}{2} – \frac{x^3}{3} \right]_{0}^{1} = \pi \left( \frac{1}{2} – \frac{1}{3} \right) = \frac{\pi}{6}$$
Kết luận: Thể tích là $\frac{\pi}{6}$ đơn vị khối.
Dạng 5: Quay quanh trục Oy
Bài tập 5: Tính thể tích khi quay $x = y^2$ từ $y = 0$ đến $y = 1$ quanh trục Oy.
Lời giải:
$$V = \pi \int_{0}^{1} (y^2)^2 , dy = \pi \int_{0}^{1} y^4 , dy$$ $$= \pi \left[ \frac{y^5}{5} \right]_{0}^{1} = \frac{\pi}{5}$$
Kết luận: Thể tích là $\frac{\pi}{5}$ đơn vị khối.
Dạng 6: Quay hàm mũ và logarit
Bài tập 6: Tính thể tích khi quay $y = e^x$ từ $x = 0$ đến $x = 1$ quanh trục Ox.
Lời giải:
$$V = \pi \int_{0}^{1} (e^x)^2 , dx = \pi \int_{0}^{1} e^{2x} , dx$$ $$= \pi \left[ \frac{e^{2x}}{2} \right]_{0}^{1} = \pi \left( \frac{e^2}{2} – \frac{1}{2} \right) = \frac{\pi(e^2 – 1)}{2}$$
Kết luận: Thể tích là $\frac{\pi(e^2 – 1)}{2} \approx 10.04$ đơn vị khối.
VI. MẸO VÀ LƯU Ý
1. Các sai lầm thường gặp
❌ SAI LẦM 1: Quên bình phương hàm số
Sai:
- $V = \pi \int y , dx$ ❌
Đúng:
- $V = \pi \int y^2 , dx$ ✓
Ghi nhớ: Luôn nhớ bình phương hàm số!
❌ SAI LẦM 2: Quên nhân với $\pi$
Sai:
- $V = \int y^2 , dx$ ❌
Đúng:
- $V = \pi \int y^2 , dx$ ✓
❌ SAI LẦM 3: Nhầm lẫn công thức quay quanh Ox và Oy
Quay quanh Ox:
- $V = \pi \int y^2 , dx$ (biến $dx$)
Quay quanh Oy:
- $V = \pi \int x^2 , dy$ (biến $dy$)
❌ SAI LẦM 4: Đặt sai cận tích phân
Lưu ý:
- Phải tìm giao điểm chính xác
- Cận dưới < cận trên
- Kiểm tra lại bằng cách vẽ hình
2. Mẹo tính nhanh
🔹 Mẹo 1: Nhớ công thức các khối cơ bản
- Hình trụ: $V = \pi r^2 h$
- Hình nón: $V = \frac{1}{3}\pi r^2 h$
- Hình cầu: $V = \frac{4}{3}\pi R^3$
🔹 Mẹo 2: Kỹ thuật tính tích phân
Phân tích đa thức: $$\int (x+1)^2 , dx = \int (x^2 + 2x + 1) , dx$$
Công thức hạ bậc: $$\sin^2 x = \frac{1 – \cos 2x}{2}$$
Đổi biến: Khi gặp hàm hợp phức tạp
🔹 Mẹo 3: Kiểm tra kết quả
- Thể tích luôn dương
- So sánh với các khối cơ bản để ước lượng
- Nếu kết quả âm → Sai ở đâu đó!
3. Công thức nguyên hàm thường dùng
| Hàm số | Nguyên hàm | Ghi chú |
|---|---|---|
| $x^n$ | $\frac{x^{n+1}}{n+1} + C$ | $n \neq -1$ |
| $\frac{1}{x}$ | $\ln|x| + C$ | $x \neq 0$ |
| $e^{ax}$ | $\frac{e^{ax}}{a} + C$ | $a \neq 0$ |
| $\sin x$ | $-\cos x + C$ | |
| $\cos x$ | $\sin x + C$ | |
| $\sin^2 x$ | $\frac{x}{2} – \frac{\sin 2x}{4} + C$ | Hạ bậc |
| $\cos^2 x$ | $\frac{x}{2} + \frac{\sin 2x}{4} + C$ | Hạ bậc |
| $\frac{1}{x^2}$ | $-\frac{1}{x} + C$ | |
| $\sqrt{x}$ | $\frac{2x^{3/2}}{3} + C$ |
VII. KẾT LUẬN
Tổng kết
Bài viết đã tổng hợp đầy đủ công thức tính thể tích khối tròn xoay:
Công thức tổng quát:
- Quay quanh Ox: $V = \pi \int_{a}^{b} y^2 , dx$
- Quay quanh Oy: $V = \pi \int_{c}^{d} x^2 , dy$
- Hai đường cong: $V = \pi \int [f^2(x) – g^2(x)] , dx$
Công thức các khối cơ bản:
- Hình trụ: $V = \pi r^2 h$
- Hình nón: $V = \frac{1}{3}\pi r^2 h$
- Hình cầu: $V = \frac{4}{3}\pi R^3$
- Hình nón cụt: $V = \frac{1}{3}\pi h(R^2 + Rr + r^2)$
Phương pháp giải bài tập – 5 bước chuẩn
6 dạng bài tập thường gặp với lời giải chi tiết
Mẹo và lưu ý – tránh sai lầm phổ biến
Xem thêm các bài liên quan:
- [Công thức tích phân cơ bản – Đầy đủ nhất]
- [Ứng dụng tích phân – Tính diện tích hình phẳng]
- [Bài tập tích phân có lời giải chi tiết]
- [Công thức nguyên hàm – Bảng tra cứu nhanh]

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
