Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ TỤ ĐIỆN
- 1. Tụ điện là gì?
- 2. Các đại lượng đặc trưng
- II. CÔNG THỨC CƠ BẢN CỦA TỤ ĐIỆN
- 1. Công thức điện dung
- 2. Đơn vị điện dung
- 3. Công thức điện dung tụ phẳng
- 4. Công thức năng lượng tụ điện
- III. TỤ ĐIỆN NỐI TIẾP
- 1. Sơ đồ mạch nối tiếp
- 2. Công thức tụ điện nối tiếp
- 3. Các công thức khác cho nối tiếp
- 4. Ví dụ về tụ nối tiếp
- IV. TỤ ĐIỆN NỐI SONG SONG
- 1. Sơ đồ mạch song song
- 2. Công thức tụ điện song song
- 3. Các công thức khác cho song song
- 4. Ví dụ về tụ song song
- V. BẢNG CÔNG THỨC TỔNG HỢP
- A. Công thức cơ bản
- B. Tụ điện phẳng
- C. Ghép tụ điện – So sánh chi tiết
- D. Trường hợp đặc biệt
- E. Quy tắc nhớ nhanh
- VI. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Quy tắc kiểm tra nhanh
- 4. Quy trình giải bài tập
- VII. BÀI TẬP MẪU
- Bài 5: Mạch hỗn hợp
- VIII. KẾT LUẬN
- Điểm cần ghi nhớ
- Lời khuyên học tập
I. GIỚI THIỆU VỀ TỤ ĐIỆN
1. Tụ điện là gì?
Định nghĩa: Tụ điện là một linh kiện điện tử có khả năng tích và phóng điện tích, được cấu tạo bởi hai bản kim loại (gọi là hai bản cực) đặt gần nhau và ngăn cách bởi một lớp cách điện (gọi là điện môi).
Cấu tạo cơ bản:
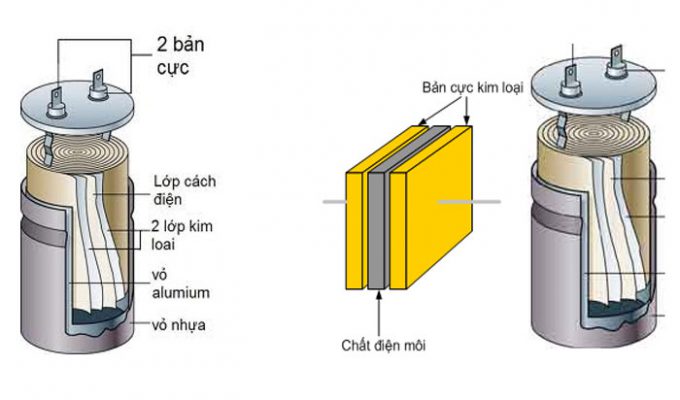
Các thành phần:
- Hai bản cực: Thường làm bằng kim loại (nhôm, đồng…) để dẫn điện tốt
- Lớp điện môi: Chất cách điện đặt giữa hai bản (không khí, giấy, gốm, plastic…)
- Vỏ bọc: Bảo vệ tụ điện khỏi môi trường bên ngoài
Ký hiệu trong mạch điện:
──┤├── (tụ điện thường - không phân cực)
──┤(├── (tụ điện phân - có phân cực)
Nguyên lý hoạt động:
- Khi đặt hiệu điện thế giữa hai bản → điện tích tích lũy trên mỗi bản
- Bản nối với cực dương: tích điện dương (+Q)
- Bản nối với cực âm: tích điện âm (-Q)
- Điện trường hình thành trong lớp điện môi
2. Các đại lượng đặc trưng
Để mô tả đầy đủ tụ điện, cần biết các đại lượng sau:
| Đại lượng | Ký hiệu | Đơn vị | Ý nghĩa |
|---|---|---|---|
| Điện dung | $C$ | F (Farad) | Khả năng tích điện của tụ |
| Điện tích | $q$, $Q$ | C (Coulomb) | Lượng điện tích trên mỗi bản |
| Hiệu điện thế | $U$ | V (Volt) | Điện áp giữa hai bản tụ |
| Năng lượng | $W$ | J (Joule) | Năng lượng điện trường tích lũy |
Giải thích chi tiết:
Điện dung (C): Là đại lượng đặc trưng cho khả năng tích điện của tụ. Điện dung càng lớn, tụ càng tích được nhiều điện tích khi đặt vào cùng một hiệu điện thế.
Điện tích (Q): Là lượng điện tích tích lũy trên mỗi bản tụ. Hai bản tụ luôn mang điện tích trái dấu nhưng có độ lớn bằng nhau.
Hiệu điện thế (U): Là hiệu điện thế giữa hai bản tụ, quyết định cường độ điện trường trong tụ.
Năng lượng (W): Là năng lượng điện trường được tích lũy trong tụ khi tích điện.
II. CÔNG THỨC CƠ BẢN CỦA TỤ ĐIỆN
1. Công thức điện dung
📌 Định nghĩa điện dung:
$$\boxed{C = \frac{Q}{U}}$$
Trong đó:
- $C$: điện dung của tụ điện, đơn vị: Farad (F)
- $Q$: điện tích trên mỗi bản tụ, đơn vị: Coulomb (C)
- $U$: hiệu điện thế giữa hai bản tụ, đơn vị: Volt (V)
Ý nghĩa vật lý:
Điện dung đặc trưng cho khả năng tích điện của tụ điện. Điện dung càng lớn thì:
- Tụ tích được càng nhiều điện tích khi đặt vào cùng hiệu điện thế
- Khả năng lưu trữ năng lượng càng lớn
- Thời gian nạp/xả điện càng lâu
Các công thức suy ra:
Từ định nghĩa trên, ta có các công thức biến đổi:
$$\boxed{Q = C \cdot U}$$
$$\boxed{U = \frac{Q}{C}}$$
Mối quan hệ: Biết 2 trong 3 đại lượng $(C, Q, U)$ → tính đại lượng còn lại.
Ví dụ 1: Một tụ điện có điện dung $C = 5\mu F$ được tích điện đến hiệu điện thế $U = 100V$. Tính điện tích trên mỗi bản tụ?
Lời giải:
Đổi đơn vị: $C = 5\mu F = 5 \times 10^{-6}F$
Áp dụng công thức: $$Q = C \cdot U = 5 \times 10^{-6} \times 100 = 5 \times 10^{-4} \text{ C}$$
Kết luận: Điện tích trên mỗi bản tụ là $Q = 5 \times 10^{-4}C = 0.5mC$
2. Đơn vị điện dung
Đơn vị chuẩn trong hệ SI:
Farad (F), được định nghĩa: $1F = 1\frac{C}{V}$
Ý nghĩa: Tụ điện có điện dung 1F nghĩa là khi đặt hiệu điện thế 1V giữa hai bản, tụ tích được điện tích 1C.
Lưu ý quan trọng: 1 Farad là đơn vị RẤT LỚN trong thực tế. Các tụ điện thông thường có điện dung nhỏ hơn nhiều.
Các đơn vị thực tế thường dùng:
| Đơn vị | Ký hiệu | Giá trị quy đổi | Ứng dụng |
|---|---|---|---|
| Microfarad | $\mu F$ | $1\mu F = 10^{-6}F$ | Tụ điện phân, tụ công suất |
| Nanofarad | $nF$ | $1nF = 10^{-9}F$ | Mạch lọc, mạch tần số cao |
| Picofarad | $pF$ | $1pF = 10^{-12}F$ | Tụ gốm, mạch RF, vi mạch |
Ví dụ chuyển đổi:
- $100\mu F = 100 \times 10^{-6}F = 10^{-4}F$
- $2200pF = 2200 \times 10^{-12}F = 2.2 \times 10^{-9}F = 2.2nF$
- $0.1\mu F = 0.1 \times 10^{-6}F = 10^{-7}F = 100nF$
Lưu ý khi tính toán: Luôn đổi về đơn vị Farad (F) trước khi thay vào công thức!
3. Công thức điện dung tụ phẳng
Tụ điện phẳng là loại tụ đơn giản nhất, gồm hai bản kim loại phẳng đặt song song với nhau.
Công thức điện dung:
$$\boxed{C = \frac{\varepsilon \cdot \varepsilon_0 \cdot S}{d}}$$
Trong đó:
- $\varepsilon$: hằng số điện môi (không có đơn vị)
- Chân không: $\varepsilon = 1$
- Không khí: $\varepsilon \approx 1$
- Giấy: $\varepsilon \approx 3.5$
- Mica: $\varepsilon \approx 5.4$
- Thủy tinh: $\varepsilon \approx 6$
- Gốm: $\varepsilon \approx 10-100$
- $\varepsilon_0 = 8.85 \times 10^{-12} \text{ F/m}$: hằng số điện (hay hằng số điện môi của chân không)
- $S$: diện tích phần đối diện của hai bản tụ (m²)
- $d$: khoảng cách giữa hai bản tụ (m)
Nhận xét từ công thức:
- Điện dung $C$ tỉ lệ thuận với diện tích $S$ → Tăng diện tích → điện dung tăng
- Điện dung $C$ tỉ lệ nghịch với khoảng cách $d$ → Giảm khoảng cách → điện dung tăng
- Điện dung $C$ tỉ lệ thuận với $\varepsilon$ → Điện môi tốt hơn → điện dung lớn hơn
Ví dụ 2: Tụ điện phẳng có diện tích mỗi bản $S = 100cm^2$, khoảng cách giữa hai bản $d = 1mm$, điện môi là không khí. Tính điện dung của tụ?
Lời giải:
Bước 1: Đổi đơn vị
- $S = 100cm^2 = 100 \times 10^{-4}m^2 = 0.01m^2$
- $d = 1mm = 0.001m$
- Không khí: $\varepsilon = 1$
Bước 2: Áp dụng công thức $$C = \frac{\varepsilon \cdot \varepsilon_0 \cdot S}{d} = \frac{1 \times 8.85 \times 10^{-12} \times 0.01}{0.001}$$
$$C = \frac{8.85 \times 10^{-14}}{10^{-3}} = 8.85 \times 10^{-11}F = 88.5pF$$
Kết luận: Điện dung của tụ là $88.5pF$
4. Công thức năng lượng tụ điện
Khi tụ điện được tích điện, năng lượng điện trường được tích lũy trong tụ.
Công thức năng lượng:
$$\boxed{W = \frac{1}{2}Q \cdot U = \frac{1}{2}C \cdot U^2 = \frac{Q^2}{2C}}$$
Ba dạng công thức tương đương:
| Biết đại lượng | Công thức năng lượng | Khi nào dùng |
|---|---|---|
| $Q$, $U$ | $W = \frac{1}{2}QU$ | Biết điện tích và hiệu điện thế |
| $C$, $U$ | $W = \frac{1}{2}CU^2$ | Biết điện dung và hiệu điện thế (phổ biến nhất) |
| $Q$, $C$ | $W = \frac{Q^2}{2C}$ | Biết điện tích và điện dung |
Đơn vị: Năng lượng đo bằng Joule (J)
Lưu ý quan trọng: Luôn có hệ số $\frac{1}{2}$ trong công thức năng lượng tụ điện!
Ví dụ 3: Một tụ điện có điện dung $C = 10\mu F$ được tích điện đến hiệu điện thế $U = 100V$. Tính:
a) Điện tích trên tụ b) Năng lượng tích lũy trong tụ
Lời giải:
Câu a) Tính điện tích:
Đổi: $C = 10\mu F = 10 \times 10^{-6}F = 10^{-5}F$
$$Q = C \cdot U = 10^{-5} \times 100 = 10^{-3}C = 1mC$$
Câu b) Tính năng lượng:
$$W = \frac{1}{2}CU^2 = \frac{1}{2} \times 10^{-5} \times (100)^2$$
$$W = \frac{1}{2} \times 10^{-5} \times 10000 = \frac{1}{2} \times 10^{-1} = 0.05J$$
Kết luận:
- Điện tích: $Q = 1mC$
- Năng lượng: $W = 0.05J = 50mJ$
III. TỤ ĐIỆN NỐI TIẾP
1. Sơ đồ mạch nối tiếp
Khi các tụ điện được mắc nối tiếp, chúng được nối liên tiếp nhau thành một chuỗi:
──┤├────┤├────┤├──
C₁ C₂ C₃
Đặc điểm:
- Các tụ mắc liên tiếp, bản âm của tụ này nối với bản dương của tụ kia
- Chỉ có một đường dẫn duy nhất cho dòng điện đi qua
2. Công thức tụ điện nối tiếp
📌 Công thức điện dung tương đương:
$$\boxed{\frac{1}{C_{td}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3} + …}$$
Đối với 2 tụ mắc nối tiếp:
$$\frac{1}{C_{td}} = \frac{1}{C_1} + \frac{1}{C_2} = \frac{C_1 + C_2}{C_1 \cdot C_2}$$
Do đó:
$$\boxed{C_{td} = \frac{C_1 \cdot C_2}{C_1 + C_2}}$$
Cách nhớ: “Tích chia tổng”
Trường hợp đặc biệt – n tụ giống nhau ($C_1 = C_2 = … = C_n = C$):
$$\boxed{C_{td} = \frac{C}{n}}$$
Nhận xét quan trọng:
- Điện dung tương đương khi nối tiếp luôn nhỏ hơn điện dung nhỏ nhất trong bộ: $C_{td} < C_{min}$
- Nối tiếp càng nhiều tụ → điện dung tương đương càng nhỏ
3. Các công thức khác cho nối tiếp
Điện tích:
Khi mắc nối tiếp, tất cả các tụ đều có cùng điện tích:
$$\boxed{Q_1 = Q_2 = Q_3 = Q_{td}}$$
Giải thích: Điện tích di chuyển từ nguồn qua các tụ nối tiếp, nên lượng điện tích trên mỗi tụ bằng nhau.
Hiệu điện thế:
Hiệu điện thế tổng bằng tổng hiệu điện thế trên từng tụ:
$$\boxed{U = U_1 + U_2 + U_3}$$
Với: $$U_i = \frac{Q}{C_i} = U \cdot \frac{C_{td}}{C_i}$$
Công thức tính $U_i$:
$$\boxed{U_i = U \cdot \frac{C_{td}}{C_i}}$$
Nhận xét: Tụ có điện dung nhỏ hơn sẽ chịu hiệu điện thế lớn hơn.
4. Ví dụ về tụ nối tiếp
Bài toán: Hai tụ điện $C_1 = 6\mu F$ và $C_2 = 3\mu F$ mắc nối tiếp với nhau, rồi đặt vào hiệu điện thế $U = 120V$. Tính:
a) Điện dung tương đương b) Điện tích trên mỗi tụ c) Hiệu điện thế trên mỗi tụ
Lời giải:
Câu a) Tính điện dung tương đương:
$$C_{td} = \frac{C_1 \cdot C_2}{C_1 + C_2} = \frac{6 \times 3}{6 + 3} = \frac{18}{9} = 2\mu F$$
Câu b) Tính điện tích:
Điện tích trên bộ tụ: $$Q_{td} = C_{td} \cdot U = 2 \times 10^{-6} \times 120 = 2.4 \times 10^{-4}C$$
Do mắc nối tiếp nên: $$Q_1 = Q_2 = Q_{td} = 2.4 \times 10^{-4}C = 0.24mC$$
Câu c) Tính hiệu điện thế:
$$U_1 = \frac{Q_1}{C_1} = \frac{2.4 \times 10^{-4}}{6 \times 10^{-6}} = 40V$$
$$U_2 = \frac{Q_2}{C_2} = \frac{2.4 \times 10^{-4}}{3 \times 10^{-6}} = 80V$$
Kiểm tra: $U_1 + U_2 = 40 + 80 = 120V = U$ ✓
Kết luận:
- Điện dung tương đương: $2\mu F$
- Điện tích trên mỗi tụ: $0.24mC$
- Hiệu điện thế: $U_1 = 40V$, $U_2 = 80V$
Nhận xét: Tụ $C_2$ nhỏ hơn nên chịu hiệu điện thế lớn hơn ($80V > 40V$)
IV. TỤ ĐIỆN NỐI SONG SONG
1. Sơ đồ mạch song song
Khi các tụ điện được mắc song song, các bản cùng cực được nối với nhau:
┌──┤├──┐
────┤ ├────
│ C₁ │
├──┤├──┤
│ C₂ │
└──┤├──┘
C₃
Đặc điểm:
- Tất cả các bản dương nối chung với nhau
- Tất cả các bản âm nối chung với nhau
- Hiệu điện thế giữa hai đầu mỗi tụ đều bằng nhau
2. Công thức tụ điện song song
📌 Công thức điện dung tương đương:
$$\boxed{C_{td} = C_1 + C_2 + C_3 + …}$$
Cách nhớ: Cộng trực tiếp các điện dung
Trường hợp đặc biệt – n tụ giống nhau ($C_1 = C_2 = … = C_n = C$):
$$\boxed{C_{td} = n \cdot C}$$
Nhận xét quan trọng:
- Điện dung tương đương khi song song luôn lớn hơn điện dung lớn nhất trong bộ: $C_{td} > C_{max}$
- Mắc song song càng nhiều tụ → điện dung tương đương càng lớn
3. Các công thức khác cho song song
Hiệu điện thế:
Khi mắc song song, tất cả các tụ đều có cùng hiệu điện thế:
$$\boxed{U_1 = U_2 = U_3 = U}$$
Giải thích: Các bản cùng cực nối chung nên có cùng điện thế, do đó hiệu điện thế giữa hai bản của mỗi tụ đều bằng nhau.
Điện tích:
Điện tích tổng bằng tổng điện tích trên từng tụ:
$$\boxed{Q_{td} = Q_1 + Q_2 + Q_3}$$
Với: $$Q_i = C_i \cdot U$$
Công thức tính $Q_i$:
$$\boxed{Q_i = C_i \cdot U}$$
Nhận xét: Tụ có điện dung lớn hơn sẽ tích điện tích nhiều hơn.
4. Ví dụ về tụ song song
Bài toán: Ba tụ điện $C_1 = 2\mu F$, $C_2 = 3\mu F$, $C_3 = 5\mu F$ mắc song song với nhau, rồi đặt vào hiệu điện thế $U = 100V$. Tính:
a) Điện dung tương đương b) Điện tích trên mỗi tụ c) Tổng điện tích trên bộ tụ
Lời giải:
Câu a) Tính điện dung tương đương:
$$C_{td} = C_1 + C_2 + C_3 = 2 + 3 + 5 = 10\mu F$$
Câu b) Tính điện tích trên mỗi tụ:
Do mắc song song nên: $U_1 = U_2 = U_3 = 100V$
$$Q_1 = C_1 \cdot U = 2 \times 10^{-6} \times 100 = 2 \times 10^{-4}C = 0.2mC$$
$$Q_2 = C_2 \cdot U = 3 \times 10^{-6} \times 100 = 3 \times 10^{-4}C = 0.3mC$$
$$Q_3 = C_3 \cdot U = 5 \times 10^{-6} \times 100 = 5 \times 10^{-4}C = 0.5mC$$
Câu c) Tính tổng điện tích:
Cách 1: Cộng điện tích từng tụ $$Q_{td} = Q_1 + Q_2 + Q_3 = 0.2 + 0.3 + 0.5 = 1.0mC$$
Cách 2: Dùng điện dung tương đương $$Q_{td} = C_{td} \cdot U = 10 \times 10^{-6} \times 100 = 10^{-3}C = 1.0mC$$
Kiểm tra: Hai cách cho kết quả giống nhau ✓
Kết luận:
- Điện dung tương đương: $10\mu F$
- Điện tích: $Q_1 = 0.2mC$, $Q_2 = 0.3mC$, $Q_3 = 0.5mC$
- Tổng điện tích: $1.0mC$
V. BẢNG CÔNG THỨC TỔNG HỢP
A. Công thức cơ bản
| Đại lượng | Công thức | Đơn vị |
|---|---|---|
| Điện dung | $C = \frac{Q}{U}$ | F (Farad) |
| Điện tích | $Q = C \cdot U$ | C (Coulomb) |
| Hiệu điện thế | $U = \frac{Q}{C}$ | V (Volt) |
| Năng lượng | $W = \frac{1}{2}CU^2 = \frac{1}{2}QU = \frac{Q^2}{2C}$ | J (Joule) |
B. Tụ điện phẳng
| Công thức | Biểu thức | Ý nghĩa |
|---|---|---|
| Điện dung | $C = \frac{\varepsilon \cdot \varepsilon_0 \cdot S}{d}$ | Phụ thuộc cấu tạo |
| Hằng số điện | $\varepsilon_0 = 8.85 \times 10^{-12}$ F/m | Hằng số vật lý |
C. Ghép tụ điện – So sánh chi tiết
| Tiêu chí | Nối tiếp | Song song |
|---|---|---|
| Sơ đồ | $──┤├────┤├──$ | $──||──$ (các tụ ghép song song) |
| Điện dung | $\frac{1}{C_{td}} = \sum \frac{1}{C_i}$ | $C_{td} = \sum C_i$ |
| Điện tích | $Q_i = Q_{td}$ (bằng nhau) | $Q_{td} = \sum Q_i$ (cộng lại) |
| Hiệu điện thế | $U = \sum U_i$ (cộng lại) | $U_i = U$ (bằng nhau) |
| $C_{td}$ so với $C_i$ | $C_{td} < C_{min}$ | $C_{td} > C_{max}$ |
D. Trường hợp đặc biệt
| Trường hợp | Nối tiếp | Song song |
|---|---|---|
| 2 tụ bất kỳ | $C_{td} = \frac{C_1 \cdot C_2}{C_1 + C_2}$ | $C_{td} = C_1 + C_2$ |
| n tụ giống nhau | $C_{td} = \frac{C}{n}$ | $C_{td} = n \cdot C$ |
| 3 tụ | $\frac{1}{C_{td}} = \frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}$ | $C_{td} = C_1 + C_2 + C_3$ |
E. Quy tắc nhớ nhanh
Ghép tụ điện NGƯỢC với ghép điện trở:
| Loại ghép | Điện trở | Tụ điện |
|---|---|---|
| Nối tiếp | $R_{td} = R_1 + R_2$ | $\frac{1}{C_{td}} = \frac{1}{C_1} + \frac{1}{C_2}$ |
| Song song | $\frac{1}{R_{td}} = \frac{1}{R_1} + \frac{1}{R_2}$ | $C_{td} = C_1 + C_2$ |
Ghi nhớ: Công thức ghép tụ HOÁN ĐỔI so với công thức ghép điện trở!
VI. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Công thức nền tảng nhất:
$$\boxed{Q = C \cdot U}$$
Cách nhớ: “Điện tích bằng Điện dung nhân Điện áp”
Từ công thức này suy ra TẤT CẢ các công thức khác!
Ghép tụ – Nhớ NGƯỢC với điện trở:
Nối tiếp tụ điện: $$\frac{1}{C_{td}} = \frac{1}{C_1} + \frac{1}{C_2}$$
Giống công thức ghép điện trở song song: $\frac{1}{R_{ss}} = \frac{1}{R_1} + \frac{1}{R_2}$
Song song tụ điện: $$C_{td} = C_1 + C_2$$
Giống công thức ghép điện trở nối tiếp: $R_{nt} = R_1 + R_2$
Cách nhớ: “Tụ điện làm NGƯỢC lại với điện trở”
Năng lượng tụ có hệ số $\frac{1}{2}$:
$$\boxed{W = \frac{1}{2}CU^2}$$
Cách nhớ: “Năng lượng tụ = NỬA C U bình”
Lưu ý: Đừng quên hệ số $\frac{1}{2}$!
Quy tắc nhanh cho 2 tụ nối tiếp:
$$C_{td} = \frac{C_1 \cdot C_2}{C_1 + C_2}$$
Cách nhớ: “Tích chia tổng”
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm công thức ghép tụ với điện trở
Sai:
- Nối tiếp tụ: $C_{td} = C_1 + C_2$ ❌
Đúng:
- Nối tiếp tụ: $\frac{1}{C_{td}} = \frac{1}{C_1} + \frac{1}{C_2}$ ✓
- Tụ điện NGƯỢC với điện trở!
❌ SAI LẦM 2: Quên hệ số $\frac{1}{2}$ trong công thức năng lượng
Sai:
- $W = CU^2$ ❌
Đúng:
- $W = \frac{1}{2}CU^2$ ✓
❌ SAI LẦM 3: Nhầm đơn vị μF, nF, pF
Sai:
- $C = 10\mu F$ → dùng thẳng $C = 10$ vào công thức ❌
Đúng:
- $C = 10\mu F = 10 \times 10^{-6}F = 10^{-5}F$ ✓
- Luôn đổi về Farad (F) trước khi tính!
❌ SAI LẦM 4: Quên đổi đơn vị diện tích và khoảng cách
Sai:
- $S = 100cm^2$ → dùng thẳng $S = 100$ vào công thức ❌
- $d = 2mm$ → dùng thẳng $d = 2$ vào công thức ❌
Đúng:
- $S = 100cm^2 = 100 \times 10^{-4}m^2 = 0.01m^2$ ✓
- $d = 2mm = 0.002m$ ✓
- Công thức tụ phẳng dùng đơn vị mét (m)!
3. Quy tắc kiểm tra nhanh
Đối với nối tiếp:
✓ $C_{td} < C_{min}$ (điện dung tương đương nhỏ hơn tụ nhỏ nhất)
✓ $Q_1 = Q_2 = Q_{td}$ (điện tích bằng nhau)
✓ $U_1 + U_2 = U$ (hiệu điện thế cộng lại)
✓ Tụ nhỏ chịu điện áp lớn: $C_1 < C_2 \Rightarrow U_1 > U_2$
Đối với song song:
✓ $C_{td} > C_{max}$ (điện dung tương đương lớn hơn tụ lớn nhất)
✓ $U_1 = U_2 = U$ (hiệu điện thế bằng nhau)
✓ $Q_1 + Q_2 = Q_{td}$ (điện tích cộng lại)
✓ Tụ lớn tích điện nhiều: $C_1 > C_2 \Rightarrow Q_1 > Q_2$
4. Quy trình giải bài tập
Dạng 1: Tính điện tích, năng lượng
Bước 1: Đổi đơn vị $C$ về Farad (F)
Bước 2: Tính điện tích: $Q = C \cdot U$
Bước 3: Tính năng lượng: $W = \frac{1}{2}CU^2$
Dạng 2: Ghép tụ nối tiếp
Bước 1: Tính $C_{td}$: $\frac{1}{C_{td}} = \frac{1}{C_1} + \frac{1}{C_2} + …$
Bước 2: Tính $Q_{td} = C_{td} \cdot U$
Bước 3: $Q_i = Q_{td}$ (điện tích mỗi tụ)
Bước 4: Tính $U_i = \frac{Q_i}{C_i}$
Dạng 3: Ghép tụ song song
Bước 1: Tính $C_{td} = C_1 + C_2 + …$
Bước 2: $U_i = U$ (hiệu điện thế mỗi tụ)
Bước 3: Tính $Q_i = C_i \cdot U$
Bước 4: $Q_{td} = \sum Q_i$
VII. BÀI TẬP MẪU
Bài 1: Tính điện tích và năng lượng cơ bản
Đề bài: Một tụ điện có điện dung $C = 20\mu F$ được tích điện đến hiệu điện thế $U = 200V$. Tính:
a) Điện tích trên mỗi bản tụ b) Năng lượng tích lũy trong tụ
Lời giải:
Câu a) Tính điện tích:
Đổi đơn vị: $C = 20\mu F = 20 \times 10^{-6}F$
$$Q = C \cdot U = 20 \times 10^{-6} \times 200$$ $$Q = 4 \times 10^{-3}C = 4mC$$
Câu b) Tính năng lượng:
$$W = \frac{1}{2}CU^2 = \frac{1}{2} \times 20 \times 10^{-6} \times (200)^2$$ $$W = \frac{1}{2} \times 20 \times 10^{-6} \times 40000$$ $$W = 0.4J$$
Kết luận:
- Điện tích: $4mC$
- Năng lượng: $0.4J$
Bài 2: Tụ điện phẳng
Đề bài: Một tụ điện phẳng có diện tích mỗi bản $S = 200cm^2$, khoảng cách giữa hai bản $d = 2mm$, điện môi là không khí. Tính điện dung của tụ?
Lời giải:
Bước 1: Đổi đơn vị
- $S = 200cm^2 = 200 \times 10^{-4}m^2 = 0.02m^2$
- $d = 2mm = 0.002m$
- Không khí: $\varepsilon = 1$
Bước 2: Áp dụng công thức tụ phẳng
$$C = \frac{\varepsilon \cdot \varepsilon_0 \cdot S}{d} = \frac{1 \times 8.85 \times 10^{-12} \times 0.02}{0.002}$$
$$C = \frac{1.77 \times 10^{-13}}{0.002} = 8.85 \times 10^{-11}F = 88.5pF$$
Kết luận: Điện dung của tụ là $88.5pF$
Bài 3: Hai tụ nối tiếp
Đề bài: Hai tụ điện $C_1 = 4\mu F$ và $C_2 = 12\mu F$ mắc nối tiếp, đặt vào hiệu điện thế $U = 100V$. Tính:
a) Điện dung tương đương b) Điện tích trên mỗi tụ c) Hiệu điện thế trên mỗi tụ
Lời giải:
Câu a) Điện dung tương đương:
$$C_{td} = \frac{C_1 \cdot C_2}{C_1 + C_2} = \frac{4 \times 12}{4 + 12} = \frac{48}{16} = 3\mu F$$
Câu b) Điện tích:
$$Q = C_{td} \cdot U = 3 \times 10^{-6} \times 100 = 3 \times 10^{-4}C$$
Do nối tiếp: $$Q_1 = Q_2 = 3 \times 10^{-4}C = 0.3mC$$
Câu c) Hiệu điện thế:
$$U_1 = \frac{Q}{C_1} = \frac{3 \times 10^{-4}}{4 \times 10^{-6}} = 75V$$
$$U_2 = \frac{Q}{C_2} = \frac{3 \times 10^{-4}}{12 \times 10^{-6}} = 25V$$
Kiểm tra: $U_1 + U_2 = 75 + 25 = 100V$ ✓
Kết luận:
- $C_{td} = 3\mu F$
- $Q_1 = Q_2 = 0.3mC$
- $U_1 = 75V$, $U_2 = 25V$
Bài 4: Ba tụ song song
Đề bài: Ba tụ điện $C_1 = C_2 = C_3 = 6\mu F$ mắc song song, đặt vào hiệu điện thế $U = 50V$. Tính:
a) Điện dung tương đương b) Tổng điện tích c) Năng lượng tổng
Lời giải:
Câu a) Điện dung tương đương:
$$C_{td} = C_1 + C_2 + C_3 = 6 + 6 + 6 = 18\mu F$$
Hoặc: $C_{td} = 3 \times 6 = 18\mu F$ (vì 3 tụ giống nhau)
Câu b) Tổng điện tích:
$$Q_{td} = C_{td} \cdot U = 18 \times 10^{-6} \times 50$$ $$Q_{td} = 9 \times 10^{-4}C = 0.9mC$$
Câu c) Năng lượng tổng:
$$W = \frac{1}{2}C_{td}U^2 = \frac{1}{2} \times 18 \times 10^{-6} \times (50)^2$$ $$W = \frac{1}{2} \times 18 \times 10^{-6} \times 2500 = 0.0225J = 22.5mJ$$
Kết luận:
- $C_{td} = 18\mu F$
- $Q_{td} = 0.9mC$
- $W = 22.5mJ$
Bài 5: Mạch hỗn hợp
Đề bài: Cho $C_1 = 2\mu F$ nối tiếp với bộ tụ ($C_2 = 3\mu F$ song song $C_3 = 6\mu F$). Đặt vào hiệu điện thế $U = 90V$. Tính điện dung tương đương của cả mạch?
Lời giải:
Bước 1: Tính song song $C_2$ và $C_3$
$$C_{23} = C_2 + C_3 = 3 + 6 = 9\mu F$$
Bước 2: Tính nối tiếp $C_1$ với $C_{23}$
$$C_{td} = \frac{C_1 \cdot C_{23}}{C_1 + C_{23}} = \frac{2 \times 9}{2 + 9} = \frac{18}{11} \approx 1.64\mu F$$
Kết luận: Điện dung tương đương của cả mạch là $\frac{18}{11}\mu F \approx 1.64\mu F$
VIII. KẾT LUẬN
Bài viết đã trình bày đầy đủ và chi tiết về công thức tụ điện:
Công thức cơ bản:
- Điện dung: $C = \frac{Q}{U}$ → $Q = CU$
- Năng lượng: $W = \frac{1}{2}CU^2 = \frac{1}{2}QU = \frac{Q^2}{2C}$
Tụ điện phẳng:
- $C = \frac{\varepsilon \cdot \varepsilon_0 \cdot S}{d}$
- $\varepsilon_0 = 8.85 \times 10^{-12}F/m$
Ghép tụ điện:
- Nối tiếp: $\frac{1}{C_{td}} = \sum \frac{1}{C_i}$, $Q_i = Q_{td}$, $U = \sum U_i$
- Song song: $C_{td} = \sum C_i$, $U_i = U$, $Q_{td} = \sum Q_i$
5 bài tập mẫu có lời giải chi tiết từng bước
Điểm cần ghi nhớ
📌 Công thức nền tảng: $Q = CU$ – từ đây suy ra tất cả!
📌 Ghép tụ NGƯỢC điện trở:
- Nối tiếp tụ ↔ Song song điện trở
- Song song tụ ↔ Nối tiếp điện trở
📌 Năng lượng có $\frac{1}{2}$: $W = \frac{1}{2}CU^2$ (đừng quên!)
📌 Đổi đơn vị:
- $1\mu F = 10^{-6}F$
- $1nF = 10^{-9}F$
- $1pF = 10^{-12}F$
📌 Kiểm tra nhanh:
- Nối tiếp: $C_{td} < C_{min}$, $Q$ bằng nhau, $U$ cộng lại
- Song song: $C_{td} > C_{max}$, $U$ bằng nhau, $Q$ cộng lại
Lời khuyên học tập
📌 Nhớ công thức gốc: $Q = CU$ là quan trọng nhất
📌 Phân biệt rõ: Ghép tụ NGƯỢC với ghép điện trở
📌 Luyện tập: Làm nhiều bài từ cơ bản đến nâng cao
📌 Kiểm tra đơn vị: Luôn đổi về F, C, V trước khi tính
📌 Vẽ sơ đồ: Giúp hình dung rõ cách ghép nối tiếp hay song song
📌 Kiểm tra kết quả: Dùng các quy tắc kiểm tra nhanh

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
