Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. HIỆN TƯỢNG KHÚC XẠ ÁNH SÁNG
- 1. Hiện tượng khúc xạ là gì?
- 2. Các khái niệm cơ bản
- 3. Quan sát thực tế
- II. ĐỊNH LUẬT KHÚC XẠ ÁNH SÁNG
- 1. Phát biểu định luật
- 2. Công thức định luật khúc xạ
- 3. Ý nghĩa công thức
- III. CHIẾT SUẤT CỦA MÔI TRƯỜNG
- 1. Chiết suất tuyệt đối
- 2. Bảng chiết suất một số môi trường
- 3. Chiết suất tỉ đối
- 4. Ví dụ tính toán
- IV. TÍNH CHẤT VÀ QUY LUẬT
- 1. Tính chất của hiện tượng khúc xạ
- 2. So sánh góc tới và góc khúc xạ
- 3. Quy tắc nhớ nhanh
- V. THÍ NGHIỆM VỀ ĐỊNH LUẬT KHÚC XẠ
- 1. Thí nghiệm cơ bản với bán trụ thủy tinh
- 2. Hiện tượng quan sát
- VI. ỨNG DỤNG CỦA ĐỊNH LUẬT KHÚC XẠ
- 1. Thấu kính
- 2. Lăng kính
- 3. Sợi quang
- 4. Giải thích hiện tượng tự nhiên
- 5. Công nghệ hiện đại
- VII. BÀI TẬP VẬN DỤNG
- VIII. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Lưu ý khi giải bài tập
- IX. KẾT LUẬN
I. HIỆN TƯỢNG KHÚC XẠ ÁNH SÁNG
1. Hiện tượng khúc xạ là gì?
Định nghĩa: Khi ánh sáng truyền từ môi trường trong suốt này sang môi trường trong suốt khác, tia sáng bị gẫy khúc (đổi hướng) tại mặt phân cách giữa hai môi trường. Hiện tượng này được gọi là hiện tượng khúc xạ ánh sáng.
Đặc điểm quan trọng:
- Xảy ra khi ánh sáng đi qua hai môi trường trong suốt khác nhau
- Tia sáng bị gẫy khúc (đổi hướng) tại mặt phân cách
- Ngoại trừ trường hợp tia sáng chiếu vuông góc với mặt phân cách
Ví dụ thực tế dễ thấy:
- Nhìn một cái que thẳng nhúng vào nước → que có vẻ bị gãy tại mặt nước
- Nhìn cá trong hồ nước → vị trí nhìn thấy khác với vị trí thực tế của cá
- Bỏ một đồng xu vào cốc nước → đồng xu có vẻ nằm nông hơn thực tế
2. Các khái niệm cơ bản
Để hiểu rõ hiện tượng khúc xạ, cần nắm vững các khái niệm sau:
Sơ đồ mô tả hiện tượng khúc xạ:
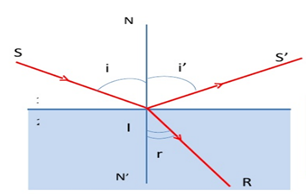
Các yếu tố cơ bản:
- Tia tới (SI): Là tia sáng chiếu đến mặt phân cách giữa hai môi trường
- Điểm tới (I): Là điểm gặp nhau giữa tia sáng và mặt phân cách
- Tia khúc xạ (IR): Là tia sáng đi vào môi trường thứ hai sau khi bị khúc xạ
- Pháp tuyến (NN’): Là đường thẳng vuông góc với mặt phân cách tại điểm tới I
- Góc tới (i): Là góc tạo bởi tia tới và pháp tuyến
- Góc khúc xạ (r): Là góc tạo bởi tia khúc xạ và pháp tuyến
- Mặt phẳng tới: Là mặt phẳng chứa tia tới và pháp tuyến
Lưu ý quan trọng:
- Góc luôn được đo từ tia sáng đến pháp tuyến, không phải đến mặt phân cách
- Pháp tuyến là đường thẳng ảo, giúp xác định các góc
3. Quan sát thực tế
Thí nghiệm đơn giản với que thẳng:
Cách làm:
- Lấy một cái que thẳng (hoặc bút chì, đũa)
- Đặt que nghiêng vào một cốc nước trong suốt
- Quan sát từ phía trên
Kết quả quan sát:
- Phần que trong nước và phần que ngoài không khí có vẻ không thẳng hàng
- Que có vẻ bị “gãy” tại mặt nước
- Góc gãy thay đổi khi thay đổi góc nghiêng của que
Giải thích:
- Ánh sáng phản xạ từ phần que trong nước bị khúc xạ khi đi ra không khí
- Do đó, mắt ta nhìn thấy ảnh của que bị lệch so với vị trí thực
Hiện tượng nhìn cá trong hồ:
Quan sát:
- Khi nhìn cá dưới nước, ta thấy cá ở vị trí nông hơn vị trí thực tế
- Vị trí cá có vẻ cao hơn so với vị trí thực
Nguyên nhân:
- Ánh sáng từ cá đi lên bị khúc xạ khi đi từ nước ra không khí
- Tia khúc xạ xa pháp tuyến hơn tia tới
- Mắt ta nhìn theo tia khúc xạ nên thấy ảnh ảo của cá cao hơn vị trí thực
Hiện tượng đồng xu trong nước:
Thí nghiệm:
- Đặt một đồng xu vào đáy cốc rỗng
- Lùi xa đến khi vừa không nhìn thấy đồng xu
- Giữ nguyên vị trí, đổ nước vào cốc
- Quan sát
Kết quả:
- Khi đổ nước vào, đồng xu lại xuất hiện trong tầm nhìn
- Đồng xu có vẻ nằm nông hơn so với thực tế
Giải thích:
- Do hiện tượng khúc xạ ánh sáng từ nước ra không khí
- Ảnh của đồng xu cao hơn vị trí thực của đồng xu
II. ĐỊNH LUẬT KHÚC XẠ ÁNH SÁNG
1. Phát biểu định luật
Định luật khúc xạ ánh sáng (còn gọi là Định luật Snell-Descartes) được phát biểu gồm hai phần:
📌 Phần 1 – Tính chất hình học:
“Tia khúc xạ nằm trong mặt phẳng tới (tức là mặt phẳng chứa tia tới và pháp tuyến) và ở bên kia pháp tuyến so với tia tới.”
Ý nghĩa:
- Cùng mặt phẳng: Tia tới, pháp tuyến và tia khúc xạ cùng nằm trong một mặt phẳng
- Khác phía: Tia tới và tia khúc xạ nằm ở hai phía của pháp tuyến
📌 Phần 2 – Công thức định lượng:
“Với hai môi trường trong suốt nhất định, tỉ số giữa sin của góc tới và sin của góc khúc xạ là một hằng số.”
Công thức toán học:
$$\frac{\sin i}{\sin r} = \text{hằng số}$$
Hoặc viết đầy đủ với chiết suất:
$$\boxed{n_1\sin i = n_2\sin r}$$
Trong đó:
- $i$: góc tới (góc giữa tia tới và pháp tuyến)
- $r$: góc khúc xạ (góc giữa tia khúc xạ và pháp tuyến)
- $n_1$: chiết suất của môi trường chứa tia tới
- $n_2$: chiết suất của môi trường chứa tia khúc xạ
Tên gọi:
- Định luật Snell (theo nhà toán học Hà Lan Willebrord Snellius, 1621)
- Định luật Snell-Descartes (thêm tên nhà triết học Pháp René Descartes)
- Định luật khúc xạ ánh sáng
2. Công thức định luật khúc xạ
Định luật khúc xạ có thể viết dưới nhiều dạng khác nhau, tùy theo đại lượng đã biết:
📌 Dạng 1 – Công thức Snell chuẩn:
$$\boxed{n_1\sin i = n_2\sin r}$$
Đây là dạng phổ biến nhất, dùng khi biết chiết suất của cả hai môi trường.
📌 Dạng 2 – Tỉ số sin góc:
$$\boxed{\frac{\sin i}{\sin r} = \frac{n_2}{n_1}}$$
Biến đổi:
- Từ $n_1\sin i = n_2\sin r$
- Chia cả hai vế cho $n_1\sin r$
- Được $\frac{\sin i}{\sin r} = \frac{n_2}{n_1}$
📌 Dạng 3 – Chiết suất tỉ đối:
$$\boxed{n_{21} = \frac{n_2}{n_1} = \frac{\sin i}{\sin r}}$$
Trong đó:
- $n_{21}$ là chiết suất tỉ đối của môi trường 2 đối với môi trường 1
- Đọc là: “en hai một”
Ý nghĩa: Chiết suất tỉ đối cho biết môi trường 2 chiết quang gấp bao nhiêu lần môi trường 1.
📌 Dạng 4 – Liên hệ với vận tốc:
Vì $n = \frac{c}{v}$, nên:
$$\frac{\sin i}{\sin r} = \frac{n_2}{n_1} = \frac{v_1}{v_2}$$
Trong đó:
- $v_1$: vận tốc ánh sáng trong môi trường 1
- $v_2$: vận tốc ánh sáng trong môi trường 2
3. Ý nghĩa công thức
Hiểu rõ ý nghĩa của công thức giúp dự đoán hướng đi của tia khúc xạ:
📍 Trường hợp 1: Từ môi trường chiết quang kém sang môi trường chiết quang hơn
Điều kiện: $n_1 < n_2$ (ví dụ: không khí → nước, không khí → thủy tinh)
Phân tích:
- Từ $n_1\sin i = n_2\sin r$ với $n_1 < n_2$
- Suy ra: $\sin i > \sin r$
- Do đó: $i > r$ (vì $0° < i, r < 90°$)
Kết luận:
- Góc khúc xạ nhỏ hơn góc tới: $r < i$
- Tia khúc xạ gần pháp tuyến hơn tia tới
- Tia sáng bị “kéo lại gần” pháp tuyến
Ví dụ:
- Không khí ($n_1 = 1$) → Nước ($n_2 = 1.33$): $n_1 < n_2$ → $r < i$
- Không khí ($n_1 = 1$) → Thủy tinh ($n_2 = 1.5$): $n_1 < n_2$ → $r < i$
📍 Trường hợp 2: Từ môi trường chiết quang hơn sang môi trường chiết quang kém
Điều kiện: $n_1 > n_2$ (ví dụ: nước → không khí, thủy tinh → không khí)
Phân tích:
- Từ $n_1\sin i = n_2\sin r$ với $n_1 > n_2$
- Suy ra: $\sin i < \sin r$
- Do đó: $i < r$
Kết luận:
- Góc khúc xạ lớn hơn góc tới: $r > i$
- Tia khúc xạ xa pháp tuyến hơn tia tới
- Tia sáng bị “đẩy ra xa” pháp tuyến
Ví dụ:
- Nước ($n_1 = 1.33$) → Không khí ($n_2 = 1$): $n_1 > n_2$ → $r > i$
- Thủy tinh ($n_1 = 1.5$) → Không khí ($n_2 = 1$): $n_1 > n_2$ → $r > i$
📍 Trường hợp 3: Tia sáng chiếu vuông góc
Điều kiện: $i = 0°$ (tia tới trùng với pháp tuyến)
Phân tích:
- Từ $n_1\sin i = n_2\sin r$
- Với $i = 0°$: $\sin 0° = 0$
- Suy ra: $\sin r = 0$
- Do đó: $r = 0°$
Kết luận:
- Tia sáng truyền thẳng, không đổi hướng
- Tia khúc xạ trùng với tia tới
Ứng dụng: Khi muốn ánh sáng không bị lệch, cần chiếu vuông góc với mặt phân cách.
III. CHIẾT SUẤT CỦA MÔI TRƯỜNG
1. Chiết suất tuyệt đối
Định nghĩa:
Chiết suất tuyệt đối (hay gọi tắt là chiết suất) của một môi trường là chiết suất tỉ đối của môi trường đó đối với chân không.
Công thức:
$$\boxed{n = \frac{c}{v}}$$
Trong đó:
- $n$: chiết suất tuyệt đối của môi trường (không có đơn vị)
- $c = 3 \times 10^8 \text{ m/s}$: tốc độ ánh sáng trong chân không
- $v$: tốc độ ánh sáng trong môi trường đó (m/s)
Ý nghĩa vật lý:
Chiết suất cho biết ánh sáng truyền trong môi trường đó chậm hơn bao nhiêu lần so với trong chân không.
Ví dụ:
- Chiết suất nước $n = 1.33$ → Ánh sáng trong nước chậm hơn 1.33 lần so với trong chân không
- Vận tốc trong nước: $v = \frac{c}{n} = \frac{3 \times 10^8}{1.33} \approx 2.26 \times 10^8$ m/s
Tính chất của chiết suất:
Tính chất 1: $n \geq 1$ với mọi môi trường
- Bằng 1 khi và chỉ khi môi trường là chân không
- Lớn hơn 1 với mọi môi trường vật chất
Tính chất 2: Môi trường chiết quang hơn có chiết suất lớn hơn
- Môi trường chiết quang hơn → $n$ lớn → $v$ nhỏ
- Ánh sáng truyền chậm hơn trong môi trường chiết quang hơn
Tính chất 3: Chiết suất phụ thuộc vào:
- Bản chất môi trường: Nước, thủy tinh, kim cương có chiết suất khác nhau
- Bước sóng ánh sáng: Ánh sáng đỏ và tím có chiết suất khác nhau trong cùng môi trường
- Nhiệt độ: Chiết suất giảm khi nhiệt độ tăng (thường không đáng kể)
2. Bảng chiết suất một số môi trường
Dưới đây là chiết suất của một số môi trường thông dụng (đối với ánh sáng vàng, ở nhiệt độ phòng):
| Môi trường | Chiết suất n | Vận tốc ánh sáng (×10⁸ m/s) |
|---|---|---|
| Chân không | 1.0000 | 3.00 |
| Không khí | 1.0003 ≈ 1 | ≈ 3.00 |
| Nước | 1.33 | 2.26 |
| Cồn (ethanol) | 1.36 | 2.21 |
| Dầu ăn | 1.47 | 2.04 |
| Thủy tinh | 1.5 (trung bình) | 2.00 |
| Thủy tinh crown | 1.52 | 1.97 |
| Thủy tinh flint | 1.6 – 1.7 | 1.76 – 1.88 |
| Kim cương | 2.42 | 1.24 |
| Băng | 1.31 | 2.29 |
Lưu ý:
- Với không khí, thường coi $n = 1$ để đơn giản hóa tính toán
- Kim cương có chiết suất rất cao → ánh sáng bị khúc xạ mạnh → tạo độ lấp lánh
- Thủy tinh có nhiều loại với chiết suất khác nhau (1.5 – 1.9)
3. Chiết suất tỉ đối
Định nghĩa:
Chiết suất tỉ đối của môi trường 2 đối với môi trường 1, ký hiệu $n_{21}$, là tỉ số giữa chiết suất tuyệt đối của hai môi trường:
$$\boxed{n_{21} = \frac{n_2}{n_1}}$$
Liên hệ với định luật khúc xạ:
Từ công thức $n_1\sin i = n_2\sin r$, ta có:
$$n_{21} = \frac{n_2}{n_1} = \frac{\sin i}{\sin r}$$
Tính chất của chiết suất tỉ đối:
Tính chất 1: Tính đối xứng $$n_{21} \cdot n_{12} = 1$$
Hoặc: $n_{21} = \frac{1}{n_{12}}$
Chứng minh: $$n_{21} = \frac{n_2}{n_1}, \quad n_{12} = \frac{n_1}{n_2}$$ $$n_{21} \cdot n_{12} = \frac{n_2}{n_1} \cdot \frac{n_1}{n_2} = 1$$
Tính chất 2: Liên hệ với vận tốc $$n_{21} = \frac{n_2}{n_1} = \frac{c/v_2}{c/v_1} = \frac{v_1}{v_2}$$
Ý nghĩa: Chiết suất tỉ đối bằng tỉ số nghịch của vận tốc.
4. Ví dụ tính toán
Ví dụ 1: Tính góc khúc xạ
Đề bài: Một tia sáng đi từ không khí vào nước với góc tới $i = 60°$. Tính góc khúc xạ. Biết chiết suất của nước $n_{nước} = 1.33$.
Lời giải:
Bước 1: Xác định dữ liệu
- Môi trường 1 (không khí): $n_1 = 1$
- Môi trường 2 (nước): $n_2 = 1.33$
- Góc tới: $i = 60°$
Bước 2: Áp dụng định luật khúc xạ $$n_1\sin i = n_2\sin r$$ $$1 \times \sin 60° = 1.33 \times \sin r$$
Bước 3: Tính $\sin r$ $$\sin r = \frac{\sin 60°}{1.33} = \frac{0.866}{1.33} \approx 0.651$$
Bước 4: Tính $r$ $$r = \arcsin(0.651) \approx 40.6°$$
Kết luận: Góc khúc xạ là khoảng $40.6°$.
Nhận xét: Vì $n_1 < n_2$ nên $r < i$ ($40.6° < 60°$), tia khúc xạ gần pháp tuyến hơn tia tới ✓
Ví dụ 2: Tính vận tốc ánh sáng
Đề bài: Chiết suất của thủy tinh là 1.5. Tính vận tốc ánh sáng trong thủy tinh.
Lời giải:
Từ công thức: $n = \frac{c}{v}$
Suy ra: $v = \frac{c}{n} = \frac{3 \times 10^8}{1.5} = 2 \times 10^8 \text{ m/s}$
Kết luận: Vận tốc ánh sáng trong thủy tinh là $2 \times 10^8$ m/s.
IV. TÍNH CHẤT VÀ QUY LUẬT
1. Tính chất của hiện tượng khúc xạ
a) Tính thuận nghịch của đường truyền ánh sáng:
Phát biểu: Nếu tia sáng đi theo đường SI → IR (từ môi trường 1 sang môi trường 2) thì tia sáng đi ngược lại theo đường IR → SI (từ môi trường 2 sang môi trường 1) cũng tuân theo định luật khúc xạ.
Chứng minh toán học:
Chiều thuận (1 → 2): $$n_1\sin i = n_2\sin r$$
Chiều ngược (2 → 1): Đổi vai trò các góc và môi trường $$n_2\sin r = n_1\sin i$$
Hai công thức giống hệt nhau → Tính thuận nghịch được chứng minh ✓
Ứng dụng: Khi thiết kế hệ quang học, có thể tính toán theo chiều thuận hoặc ngược đều được.
b) Tia khúc xạ nằm trong mặt phẳng tới:
Phát biểu: Tia tới, tia khúc xạ và pháp tuyến luôn cùng nằm trong một mặt phẳng (gọi là mặt phẳng tới).
Ý nghĩa: Hiện tượng khúc xạ là hiện tượng phẳng, chỉ cần khảo sát trong một mặt phẳng.
c) Tia khúc xạ và tia tới ở hai bên pháp tuyến:
Phát biểu: Tia tới và tia khúc xạ luôn nằm ở hai phía khác nhau của pháp tuyến tại điểm tới.
Lưu ý: Điều này phân biệt khúc xạ với phản xạ (trong phản xạ, tia phản xạ ở cùng phía với tia tới).
2. So sánh góc tới và góc khúc xạ
Để dự đoán nhanh hướng đi của tia khúc xạ, ta cần so sánh góc tới và góc khúc xạ:
📌 Trường hợp 1: Ánh sáng từ môi trường kém sang môi trường chiết quang hơn
Điều kiện:
- $n_1 < n_2$
- Môi trường 1 chiết quang kém hơn môi trường 2
Kết luận:
- $i > r$ (góc khúc xạ nhỏ hơn góc tới)
- Tia khúc xạ gần pháp tuyến hơn tia tới
- Tia sáng bị “kéo lại gần” pháp tuyến
Ví dụ cụ thể:
- Không khí → Nước: $n_1 = 1 < n_2 = 1.33$ → $r < i$
- Không khí → Thủy tinh: $n_1 = 1 < n_2 = 1.5$ → $r < i$
- Nước → Thủy tinh: $n_1 = 1.33 < n_2 = 1.5$ → $r < i$
Hình ảnh minh họa: Tia khúc xạ nghiêng về phía pháp tuyến
📌 Trường hợp 2: Ánh sáng từ môi trường chiết quang hơn sang môi trường kém
Điều kiện:
- $n_1 > n_2$
- Môi trường 1 chiết quang hơn môi trường 2
Kết luận:
- $i < r$ (góc khúc xạ lớn hơn góc tới)
- Tia khúc xạ xa pháp tuyến hơn tia tới
- Tia sáng bị “đẩy ra xa” pháp tuyến
Ví dụ cụ thể:
- Nước → Không khí: $n_1 = 1.33 > n_2 = 1$ → $r > i$
- Thủy tinh → Không khí: $n_1 = 1.5 > n_2 = 1$ → $r > i$
- Thủy tinh → Nước: $n_1 = 1.5 > n_2 = 1.33$ → $r > i$
Lưu ý đặc biệt: Khi $i$ đủ lớn, có thể xảy ra phản xạ toàn phần (không có tia khúc xạ).
📌 Trường hợp đặc biệt: Tia sáng chiếu vuông góc
Điều kiện: $i = 0°$ (tia tới vuông góc với mặt phân cách, trùng với pháp tuyến)
Kết luận:
- $r = 0°$
- Tia sáng truyền thẳng, không đổi hướng
- Tia khúc xạ trùng với tia tới và pháp tuyến
Ứng dụng: Để tránh hiện tượng lệch ảnh, cần đặt vật vuông góc với tia sáng.
3. Quy tắc nhớ nhanh
Để nhớ mối quan hệ giữa góc tới và góc khúc xạ, có thể dùng các quy tắc sau:
Quy tắc 1: “Kém sang hơn – Lại gần”
Ý nghĩa:
- Từ môi trường chiết quang kém → môi trường chiết quang hơn
- Tia khúc xạ lại gần pháp tuyến hơn
- $r < i$
Ví dụ: Không khí ($n=1$) → Nước ($n=1.33$): Tia khúc xạ gần pháp tuyến hơn
Quy tắc 2: “Hơn sang kém – Ra xa”
Ý nghĩa:
- Từ môi trường chiết quang hơn → môi trường chiết quang kém
- Tia khúc xạ ra xa pháp tuyến hơn
- $r > i$
Ví dụ: Nước ($n=1.33$) → Không khí ($n=1$): Tia khúc xạ xa pháp tuyến hơn
Quy tắc 3: Nhớ bằng hình ảnh
Hình ảnh: Tưởng tượng một người đi từ đường bê tông (dễ đi, nhanh) vào ruộng bùn (khó đi, chậm)
- Khi vào ruộng bùn, người sẽ tự động đi vuông góc với bờ ruộng để giảm quãng đường đi trong bùn
- Tương tự, ánh sáng từ không khí (nhanh) vào nước (chậm) sẽ lại gần pháp tuyến (gần vuông góc với mặt nước)
V. THÍ NGHIỆM VỀ ĐỊNH LUẬT KHÚC XẠ
1. Thí nghiệm cơ bản với bán trụ thủy tinh
Mục đích:
Kiểm chứng định luật khúc xạ ánh sáng và đo chiết suất của thủy tinh.
Dụng cụ thí nghiệm:
- Bán trụ thủy tinh (hoặc khối thủy tinh hình chữ nhật)
- Đèn chiếu tia sáng hẹp (laser hoặc đèn khe)
- Giá đỡ có chia độ (đĩa quang học)
- Thước đo góc (hoặc giấy kẻ ô vuông)
- Giấy trắng để đánh dấu đường đi của tia sáng
Tiến hành thí nghiệm:
Bước 1: Đặt bán trụ thủy tinh trên giá chia độ, mặt phẳng nằm sát giấy
Bước 2: Chiếu tia sáng vào mặt phẳng của bán trụ tại tâm O (tránh khúc xạ khi ra khỏi mặt cong)
Bước 3: Thay đổi góc tới $i$ (ví dụ: $0°, 30°, 45°, 60°$)
Bước 4: Đo góc khúc xạ $r$ tương ứng với mỗi góc tới
Bước 5: Lập bảng giá trị $i$, $r$, $\sin i$, $\sin r$, $\frac{\sin i}{\sin r}$
Bước 6: Tính giá trị trung bình của $\frac{\sin i}{\sin r}$ để tìm chiết suất
Bảng kết quả mẫu:
| Góc tới i | Góc khúc xạ r | sin i | sin r | n = sin i / sin r |
|---|---|---|---|---|
| 0° | 0° | 0 | 0 | – |
| 30° | 19.5° | 0.500 | 0.333 | 1.50 |
| 45° | 28.1° | 0.707 | 0.471 | 1.50 |
| 60° | 35.3° | 0.866 | 0.577 | 1.50 |
| Trung bình | 1.50 |
Kết luận từ thí nghiệm:
- Tỉ số $\frac{\sin i}{\sin r} \approx 1.5$ = hằng số → Xác nhận định luật khúc xạ
- Chiết suất thủy tinh: $n \approx 1.5$
2. Hiện tượng quan sát
Quan sát 1: Khi góc tới tăng, góc khúc xạ cũng tăng
- Nhưng tốc độ tăng của $r$ chậm hơn tốc độ tăng của $i$
- Lý do: $i$ luôn lớn hơn $r$ (vì ánh sáng từ không khí vào thủy tinh)
Quan sát 2: Khi $i = 0°$ → $r = 0°$
- Tia sáng chiếu vuông góc → truyền thẳng, không đổi hướng
- Xác nhận tính chất đặc biệt của khúc xạ
Quan sát 3: Tia khúc xạ luôn gần pháp tuyến hơn tia tới
- Vì ánh sáng từ môi trường chiết quang kém (không khí, $n=1$) vào môi trường chiết quang hơn (thủy tinh, $n=1.5$)
VI. ỨNG DỤNG CỦA ĐỊNH LUẬT KHÚC XẠ
1. Thấu kính
Nguyên lý:
Thấu kính hoạt động dựa trên hiện tượng khúc xạ ánh sáng qua các mặt cong.
Hai loại thấu kính:
- Thấu kính hội tụ: Dày giữa, mỏng rìa → hội tụ tia sáng
- Thấu kính phân kỳ: Mỏng giữa, dày rìa → phân kỳ tia sáng
Ứng dụng thực tế:
- Kính mắt: Kính cận (phân kỳ), kính viễn (hội tụ), kính lão (đa tròng)
- Máy ảnh: Hệ thống nhiều thấu kính để tạo ảnh rõ nét
- Kính hiển vi: Phóng đại vật nhỏ
- Kính thiên văn: Quan sát các thiên thể xa
- Kính lúp: Đọc sách, quan sát chi tiết nhỏ
2. Lăng kính
Nguyên lý:
Lăng kính là khối thủy tinh trong suốt có tiết diện tam giác. Ánh sáng bị khúc xạ hai lần khi đi qua lăng kính.
Hiện tượng tán sắc:
- Ánh sáng trắng qua lăng kính → phân tách thành nhiều màu (cầu vồng)
- Nguyên nhân: Chiết suất phụ thuộc vào bước sóng (màu sắc)
- Ánh sáng tím bị lệch nhiều nhất, ánh sáng đỏ bị lệch ít nhất
Ứng dụng:
- Máy quang phổ: Phân tích thành phần ánh sáng
- Đo chiết suất: Xác định chiết suất của vật liệu
- Trang trí: Hiệu ứng ánh sáng đẹp mắt
3. Sợi quang
Nguyên lý:
Sợi quang hoạt động dựa trên hiện tượng phản xạ toàn phần (liên quan mật thiết đến khúc xạ).
Cấu tạo:
- Lõi trong suốt (chiết suất cao)
- Vỏ bọc (chiết suất thấp)
- Ánh sáng truyền trong lõi, phản xạ toàn phần tại mặt tiếp xúc
Ứng dụng:
- Internet cáp quang: Truyền dữ liệu tốc độ cao
- Nội soi y học: Quan sát bên trong cơ thể
- Chiếu sáng trang trí: Đèn sợi quang
- Cảm biến: Đo nhiệt độ, áp suất
4. Giải thích hiện tượng tự nhiên
a) Ảo ảnh trên sa mạc (Hiện tượng Fata Morgana):
Mô tả: Người đi sa mạc thường thấy “vũng nước” ở xa, nhưng khi đến gần thì không có gì.
Giải thích:
- Lớp không khí sát mặt cát nóng hơn → chiết suất nhỏ hơn lớp trên
- Ánh sáng từ bầu trời bị khúc xạ liên tiếp qua các lớp không khí
- Tia sáng cong xuống rồi cong lên → tạo ảnh ảo của bầu trời trên mặt cát
- Người ta tưởng là nước phản chiếu bầu trời
b) Nhìn cá trong nước:
Mô tả: Vị trí cá nhìn thấy cao hơn (nông hơn) vị trí thực tế.
Giải thích:
- Ánh sáng từ cá đi lên bị khúc xạ khi ra không khí
- Tia khúc xạ xa pháp tuyến hơn (vì từ nước ra không khí)
- Mắt ta nhìn theo tia khúc xạ → thấy ảnh ảo cao hơn vị trí thực
Hệ quả: Khi bắn cá bằng súng, phải ngắm thấp hơn vị trí nhìn thấy.
c) Mặt trời mọc sớm và lặn muộn:
Mô tả: Thực tế mặt trời vẫn ở dưới đường chân trời nhưng ta đã thấy mặt trời.
Giải thích:
- Ánh sáng mặt trời bị khúc xạ qua các lớp khí quyển có mật độ khác nhau
- Tia sáng bị cong, đi theo đường cong thay vì đường thẳng
- Do đó ta thấy mặt trời sớm hơn và muộn hơn khoảng 2-3 phút
d) Cầu vồng:
Nguyên lý: Kết hợp khúc xạ, phản xạ toàn phần và tán sắc ánh sáng trong giọt nước.
5. Công nghệ hiện đại
Camera smartphone:
- Sử dụng hệ thống nhiều thấu kính (3-5 ống kính)
- Ống kính góc rộng, tele, macro → đều dựa trên nguyên lý khúc xạ
Kính thực tế ảo (VR):
- Thấu kính Fresnel để tạo ảnh ảo gần mắt
- Dựa trên khúc xạ ánh sáng qua thấu kính đặc biệt
Máy chiếu (Projector):
- Hệ thống thấu kính phóng to ảnh lên màn hình
- Khúc xạ qua thấu kính hội tụ
Kính thiên văn:
- Kính thiên văn khúc xạ dùng thấu kính để hội tụ ánh sáng
- Quan sát các thiên thể xa hàng triệu năm ánh sáng
VII. BÀI TẬP VẬN DỤNG
Dạng 1: Tính góc khúc xạ
Bài tập 1: Chiếu một tia sáng từ không khí vào nước với góc tới $45°$. Tính góc khúc xạ. Biết chiết suất của nước $n_{nước} = \frac{4}{3}$.
Lời giải:
Bước 1: Xác định dữ liệu
- Môi trường 1 (không khí): $n_1 = 1$
- Môi trường 2 (nước): $n_2 = \frac{4}{3}$
- Góc tới: $i = 45°$
Bước 2: Áp dụng định luật khúc xạ $$n_1\sin i = n_2\sin r$$ $$1 \times \sin 45° = \frac{4}{3} \times \sin r$$
Bước 3: Tính $\sin r$ $$\sin r = \frac{3\sin 45°}{4} = \frac{3 \times 0.707}{4} = \frac{2.121}{4} \approx 0.530$$
Bước 4: Tính góc $r$ $$r = \arcsin(0.530) \approx 32°$$
Đáp số: Góc khúc xạ là khoảng $32°$.
Nhận xét: Vì $n_1 < n_2$ (từ kém sang hơn) nên $r < i$ ($32° < 45°$), tia khúc xạ gần pháp tuyến hơn ✓
Dạng 2: Tính chiết suất của môi trường
Bài tập 2: Một tia sáng đi từ không khí vào một môi trường trong suốt với góc tới $60°$ và góc khúc xạ $30°$. Tính chiết suất của môi trường đó.
Lời giải:
Bước 1: Xác định dữ liệu
- Môi trường 1 (không khí): $n_1 = 1$
- Môi trường 2 (chưa biết): $n_2 = ?$
- Góc tới: $i = 60°$
- Góc khúc xạ: $r = 30°$
Bước 2: Áp dụng định luật khúc xạ $$n_1\sin i = n_2\sin r$$ $$1 \times \sin 60° = n_2 \times \sin 30°$$
Bước 3: Tính $n_2$ $$n_2 = \frac{\sin 60°}{\sin 30°} = \frac{0.866}{0.5} = 1.732$$
Bước 4: Nhận dạng môi trường $$n_2 \approx \sqrt{3} \approx 1.732$$
Đáp số: Chiết suất của môi trường là $\sqrt{3} \approx 1.732$ (có thể là một loại thủy tinh đặc biệt).
Dạng 3: Tính vận tốc ánh sáng trong môi trường
Bài tập 3: Chiết suất của nước là $\frac{4}{3}$. Tính vận tốc ánh sáng trong nước. Biết vận tốc ánh sáng trong chân không là $c = 3 \times 10^8$ m/s.
Lời giải:
Bước 1: Áp dụng công thức chiết suất $$n = \frac{c}{v}$$
Bước 2: Suy ra vận tốc $$v = \frac{c}{n} = \frac{3 \times 10^8}{4/3} = \frac{3 \times 10^8 \times 3}{4} = \frac{9 \times 10^8}{4} = 2.25 \times 10^8 \text{ m/s}$$
Đáp số: Vận tốc ánh sáng trong nước là $2.25 \times 10^8$ m/s hay $2,25 \times 10^8$ m/s.
Nhận xét: Ánh sáng trong nước chậm hơn trong chân không, đúng như lý thuyết ✓
Dạng 4: Bài toán tổng hợp – Khúc xạ qua nhiều môi trường
Bài tập 4: Một tia sáng truyền qua 3 môi trường: không khí ($n_1 = 1$) → thủy tinh ($n_2 = 1.5$) → nước ($n_3 = 1.33$). Góc tới ở môi trường 1 là $60°$. Tính góc khúc xạ cuối cùng ở môi trường 3.
Lời giải:
Phương pháp: Áp dụng liên tiếp định luật khúc xạ, hoặc dùng tính chất:
$$n_1\sin i_1 = n_2\sin i_2 = n_3\sin i_3$$
Bước 1: Áp dụng công thức liên tiếp $$n_1\sin i_1 = n_3\sin i_3$$ $$1 \times \sin 60° = 1.33 \times \sin i_3$$
Bước 2: Tính $\sin i_3$ $$\sin i_3 = \frac{\sin 60°}{1.33} = \frac{0.866}{1.33} \approx 0.651$$
Bước 3: Tính góc $i_3$ $$i_3 = \arcsin(0.651) \approx 40.6°$$
Đáp số: Góc khúc xạ ở môi trường nước là khoảng $40.6°$.
Lưu ý: Môi trường 2 (thủy tinh) không ảnh hưởng đến góc khúc xạ cuối cùng, chỉ cần biết $n_1$ và $n_3$.
Dạng 5: Bài toán ngược – Tìm góc tới
Bài tập 5: Một tia sáng đi từ thủy tinh ($n = 1.5$) ra không khí. Biết góc khúc xạ là $60°$. Tính góc tới.
Lời giải:
Bước 1: Xác định dữ liệu
- Môi trường 1 (thủy tinh): $n_1 = 1.5$
- Môi trường 2 (không khí): $n_2 = 1$
- Góc khúc xạ: $r = 60°$
- Góc tới: $i = ?$
Bước 2: Áp dụng định luật khúc xạ $$n_1\sin i = n_2\sin r$$ $$1.5 \times \sin i = 1 \times \sin 60°$$
Bước 3: Tính $\sin i$ $$\sin i = \frac{\sin 60°}{1.5} = \frac{0.866}{1.5} \approx 0.577$$
Bước 4: Tính góc $i$ $$i = \arcsin(0.577) \approx 35.3°$$
Đáp số: Góc tới là khoảng $35.3°$.
Nhận xét: Vì $n_1 > n_2$ (từ hơn sang kém) nên $i < r$ ($35.3° < 60°$), tia khúc xạ xa pháp tuyến hơn ✓
VIII. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Công thức cơ bản – Định luật Snell:
$$\boxed{n_1\sin i = n_2\sin r}$$
Cách nhớ:
“en một sin i bằng en hai sin r”
Hoặc viết thành thơ:
“n1 sin i, n2 sin r, bằng nhau thì mới là khúc xạ”
Công thức chiết suất:
$$\boxed{n = \frac{c}{v}}$$
Cách nhớ:
“en bằng xê chia vê” (n = c/v)
Hoặc:
“Chiết suất bằng tốc độ ánh sáng chân không chia tốc độ trong môi trường”
Quy tắc so sánh góc:
Từ kém → hơn: $r < i$ (gần pháp tuyến) Từ hơn → kém: $r > i$ (xa pháp tuyến)
Cách nhớ:
“Kém sang hơn – Lại gần”
“Hơn sang kém – Ra xa”
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm góc tới và góc khúc xạ
Cách phân biệt:
- Góc tới (i): Góc ở môi trường chứa tia tới (môi trường ban đầu)
- Góc khúc xạ (r): Góc ở môi trường chứa tia khúc xạ (môi trường sau)
Ví dụ: Không khí → Nước
- Góc tới: góc trong không khí
- Góc khúc xạ: góc trong nước
❌ SAI LẦM 2: Nhầm chiết suất $n_1$ và $n_2$
Quy tắc:
- $n_1$: chiết suất môi trường chứa tia tới
- $n_2$: chiết suất môi trường chứa tia khúc xạ
Kiểm tra: Luôn ghi rõ “môi trường 1” và “môi trường 2” trước khi tính toán.
❌ SAI LẦM 3: Quên điều kiện $n \geq 1$
Lưu ý:
- Chiết suất luôn lớn hơn hoặc bằng 1
- Nếu tính ra $n < 1$ → Sai ngay
❌ SAI LẦM 4: Nhầm so sánh góc khi thay đổi môi trường
Nhầm lẫn phổ biến:
- Từ không khí → nước: Tưởng $r > i$ (SAI!)
- Đúng: Từ không khí → nước: $r < i$ (vì từ kém sang hơn)
Cách tránh: Luôn kiểm tra $n_1$ so với $n_2$ trước khi kết luận.
❌ SAI LẦM 5: Đo góc từ mặt phân cách thay vì pháp tuyến
Lưu ý quan trọng:
- Góc luôn đo từ tia sáng đến pháp tuyến, KHÔNG phải đến mặt phân cách
- Nếu đề bài cho góc với mặt phân cách, phải đổi: góc với pháp tuyến = $90° -$ góc với mặt phân cách
3. Lưu ý khi giải bài tập
Lưu ý 1: Vẽ hình cẩn thận
- Vẽ rõ mặt phân cách, pháp tuyến
- Đánh dấu tia tới, tia khúc xạ
- Ghi rõ các góc $i$ và $r$
Lưu ý 2: Xác định đúng chiều truyền ánh sáng
- Từ môi trường nào sang môi trường nào?
- $n_1$ là gì, $n_2$ là gì?
Lưu ý 3: Với không khí, coi $n = 1$
- Trong hầu hết bài tập, chiết suất không khí $n_{kk} \approx 1$
- Để chính xác: $n_{kk} = 1.0003$, nhưng thường bỏ qua
Lưu ý 4: Khi $i = 0°$ (chiếu vuông góc)
- Tia sáng không đổi hướng: $r = 0°$
- Ánh sáng truyền thẳng qua mặt phân cách
Lưu ý 5: Đơn vị góc
- Có thể tính bằng độ (°) hoặc radian (rad)
- Máy tính phải để đúng chế độ (DEG hoặc RAD)
IX. KẾT LUẬN
Bài viết đã trình bày đầy đủ và chi tiết về định luật khúc xạ ánh sáng:
Hiện tượng khúc xạ:
- Ánh sáng bị gẫy khúc khi đi qua mặt phân cách giữa hai môi trường trong suốt
- Quan sát được qua nhiều hiện tượng thực tế: que nhúng nước, nhìn cá dưới hồ
Định luật khúc xạ (Định luật Snell-Descartes):
- Phần 1: Tia khúc xạ nằm trong mặt phẳng tới, khác phía với tia tới
- Phần 2: $n_1\sin i = n_2\sin r$
Chiết suất:
- Chiết suất tuyệt đối: $n = \frac{c}{v}$
- Chiết suất tỉ đối: $n_{21} = \frac{n_2}{n_1}$
Quy luật so sánh góc:
- Từ kém → hơn: $r < i$ (gần pháp tuyến)
- Từ hơn → kém: $r > i$ (xa pháp tuyến)
Ứng dụng:
- Thấu kính, lăng kính, sợi quang
- Giải thích hiện tượng tự nhiên
- Công nghệ hiện đại

ThS. Nguyễn Văn An
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Toán tại Edus
Trình độ: Cử nhân Sư phạm Toán học, Thạc sĩ Lý luận & Phương pháp dạy học môn Toán, Chức danh nghề nghiệp giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1, Chứng chỉ bồi dưỡng năng lực tổ trưởng chuyên môn
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT chuyên Trần Đại Nghĩa
