Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ LĂNG KÍNH
- 1. Lăng kính là gì?
- 2. Các đại lượng đặc trưng
- II. ĐƯỜNG ĐI CỦA TIA SÁNG QUA LĂNG KÍNH
- 1. Sơ đồ đường đi
- 2. Các bước tia sáng đi qua lăng kính
- 3. Quy ước và lưu ý
- III. CÔNG THỨC LĂNG KÍNH
- 1. Công thức khúc xạ tại các mặt bên
- 2. Công thức liên hệ các góc trong lăng kính
- 3. Công thức góc lệch
- 4. Điều kiện để có tia ló ra khỏi lăng kính
- 5. Ví dụ minh họa tổng hợp
- IV. TRƯỜNG HỢP LĂNG KÍNH GÓC NHỎ
- 1. Điều kiện góc nhỏ
- 2. Công thức đơn giản cho lăng kính góc nhỏ
- 3. Ví dụ về lăng kính góc nhỏ
- 4. Ứng dụng công thức góc nhỏ
- 5. So sánh góc lớn và góc nhỏ
- V. GÓC LỆCH CỰC TIỂU
- 1. Định nghĩa góc lệch cực tiểu
- 2. Công thức góc lệch cực tiểu
- 3. Ý nghĩa của góc lệch cực tiểu
- 4. Ví dụ tính góc lệch cực tiểu
- VI. QUANG PHỔ VÀ TÁN SẮC ÁNH SÁNG
- 1. Hiện tượng tán sắc ánh sáng
- 2. Quang phổ liên tục của ánh sáng trắng
- 3. Góc tán sắc
- 4. Ứng dụng của tán sắc ánh sáng
- VII. BẢNG CÔNG THỨC TỔNG HỢP
- A. Công thức chính (quan trọng nhất)
- B. Công thức lăng kính góc nhỏ
- C. Công thức góc lệch cực tiểu
- D. Điều kiện tia ló và góc giới hạn
- VIII. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Kiểm tra kết quả
- IX. BÀI TẬP MẪU
- X. KẾT LUẬN
- Tổng kết
- Lời khuyên học tập
I. GIỚI THIỆU VỀ LĂNG KÍNH
1. Lăng kính là gì?
Định nghĩa: Lăng kính là một khối chất trong suốt, đồng chất (thủy tinh, nhựa, nước…), được giới hạn bởi hai mặt phẳng không song song, cắt nhau theo một đường thẳng.

Cấu tạo cơ bản của lăng kính:
A (đỉnh)
/│\
/ │ \
/ │ \
/ │ \
/____|____\
B │ C
(cạnh đáy)
Các thành phần chính:
- Đỉnh (A): Là đỉnh của lăng kính, giao tuyến của hai mặt phẳng bên
- Cạnh đáy (BC): Cạnh đối diện với đỉnh A
- Góc chiết quang (A): Góc hợp bởi hai mặt bên của lăng kính, còn gọi là góc ở đỉnh
- Mặt bên (AB và AC): Hai mặt phẳng khúc xạ, nơi ánh sáng đi vào và đi ra
- Tiết diện thẳng: Mặt phẳng vuông góc với cạnh đỉnh (thường là tam giác ABC)
Đặc điểm:
- Chất liệu trong suốt: thủy tinh, nhựa, thạch anh…
- Đồng chất: cùng một loại vật liệu
- Hai mặt bên không song song (khác với bản mặt song song)
2. Các đại lượng đặc trưng
Để nghiên cứu lăng kính, chúng ta cần nắm vững các đại lượng vật lý sau:
| Đại lượng | Ký hiệu | Ý nghĩa |
|---|---|---|
| Góc chiết quang | $A$ | Góc ở đỉnh lăng kính (góc giữa hai mặt bên) |
| Chiết suất | $n$ | Chiết suất tuyệt đối của lăng kính (so với chân không) |
| Góc tới | $i_1$ | Góc giữa tia tới và pháp tuyến tại mặt AB |
| Góc khúc xạ thứ nhất | $r_1$ | Góc giữa tia khúc xạ và pháp tuyến tại mặt AB |
| Góc tới trong | $r_2$ | Góc giữa tia tới và pháp tuyến tại mặt AC (trong lăng kính) |
| Góc ló | $i_2$ | Góc giữa tia ló và pháp tuyến tại mặt AC |
| Góc lệch | $D$ | Góc hợp bởi tia tới và tia ló |
Lưu ý quan trọng:
- Môi trường bên ngoài thường là không khí có chiết suất $n_0 = 1$
- Chiết suất lăng kính: $n > 1$ (thường từ 1.5 đến 1.9)
- Góc chiết quang A thường nhỏ (từ 30° đến 90°, phổ biến là 60°)
II. ĐƯỜNG ĐI CỦA TIA SÁNG QUA LĂNG KÍNH
1. Sơ đồ đường đi
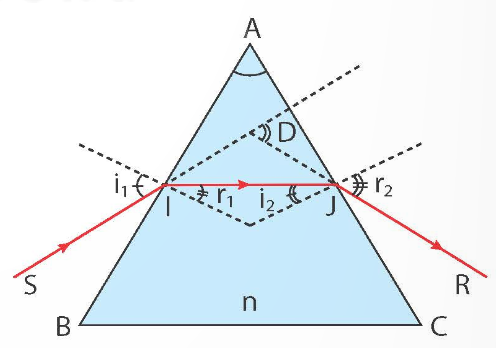
Giải thích sơ đồ:
- Tia sáng tới mặt AB tại điểm I với góc tới $i_1$
- Khúc xạ vào trong lăng kính với góc khúc xạ $r_1$
- Truyền trong lăng kính đến mặt AC tại điểm J
- Khúc xạ ra ngoài không khí với góc ló $i_2$
- Tia ló bị lệch so với phương ban đầu một góc D (góc lệch)
2. Các bước tia sáng đi qua lăng kính
Bước 1: Khúc xạ lần thứ nhất tại mặt AB (điểm I)
Tia sáng đi từ không khí (chiết suất $n_0 = 1$) vào lăng kính (chiết suất $n > 1$):
- Góc tới: $i_1$ (góc giữa tia tới và pháp tuyến tại I)
- Góc khúc xạ: $r_1$ (góc giữa tia khúc xạ và pháp tuyến tại I)
- Vì $n > n_0$ nên $r_1 < i_1$ (tia khúc xạ gần pháp tuyến hơn tia tới)
Bước 2: Truyền trong lăng kính
Tia sáng truyền thẳng trong lăng kính từ điểm I đến điểm J trên mặt AC.
Bước 3: Khúc xạ lần thứ hai tại mặt AC (điểm J)
Tia sáng đi từ lăng kính (chiết suất $n$) ra không khí (chiết suất $n_0 = 1$):
- Góc tới: $r_2$ (góc giữa tia tới trong lăng kính và pháp tuyến tại J)
- Góc ló: $i_2$ (góc giữa tia ló và pháp tuyến tại J)
- Vì $n > n_0$ nên $i_2 > r_2$ (tia ló xa pháp tuyến hơn tia tới)
Đặc điểm quan trọng: Tia ló luôn bị lệch về phía đáy của lăng kính (phía cạnh BC).
3. Quy ước và lưu ý
Quy ước về chiều dương của góc:
- Các góc được đo từ pháp tuyến
- Quy ước dương theo chiều kim đồng hồ (hoặc ngược chiều tùy giáo trình)
- Trong thực tế, ta thường chỉ quan tâm đến độ lớn của góc
Điều kiện thường gặp:
- Góc chiết quang A thường nhỏ: $A < 10°$ đến $15°$ (lăng kính góc nhỏ) hoặc $A \approx 60°$ (lăng kính chuẩn)
- Môi trường ngoài là không khí: $n_0 = 1$
- Chiết suất lăng kính: $n > 1$ (thủy tinh thường có $n \approx 1.5$ đến $1.9$)
Hiện tượng quan sát được:
- Tia sáng luôn bị lệch về phía đáy lăng kính
- Góc lệch D phụ thuộc vào góc tới $i_1$, chiết suất $n$, và góc chiết quang A
- Có một góc tới đặc biệt làm cho D đạt giá trị nhỏ nhất (góc lệch cực tiểu)
III. CÔNG THỨC LĂNG KÍNH
1. Công thức khúc xạ tại các mặt bên
Áp dụng định luật khúc xạ ánh sáng (định luật Snell-Descartes) tại mỗi mặt:
📌 Khúc xạ lần thứ nhất tại mặt AB:
$$\boxed{\sin i_1 = n \sin r_1}$$
Hoặc viết dưới dạng: $$n_0 \sin i_1 = n \sin r_1$$
Với $n_0 = 1$ (không khí)
Ý nghĩa:
- Tia sáng từ môi trường chiết quang kém (không khí) vào môi trường chiết quang hơn (lăng kính)
- $i_1 > r_1$ (tia khúc xạ bị gập lại gần pháp tuyến)
📌 Khúc xạ lần thứ hai tại mặt AC:
$$\boxed{n \sin r_2 = \sin i_2}$$
Hoặc viết dưới dạng: $$n \sin r_2 = n_0 \sin i_2$$
Với $n_0 = 1$ (không khí)
Ý nghĩa:
- Tia sáng từ môi trường chiết quang hơn (lăng kính) ra môi trường chiết quang kém (không khí)
- $i_2 > r_2$ (tia khúc xạ bị bẻ ra xa pháp tuyến)
2. Công thức liên hệ các góc trong lăng kính
📌 Công thức góc chiết quang:
$$\boxed{A = r_1 + r_2}$$
Chứng minh (hình học):
Xét tam giác IJK trong lăng kính (K là điểm bất kỳ trên cạnh đỉnh):
- Tại I: góc giữa tia khúc xạ và mặt AB là $r_1$
- Tại J: góc giữa tia tới trong và mặt AC là $r_2$
- Từ hình học tam giác: tổng các góc trong tam giác bằng 180°
- Sau khi phân tích hình học: $A = r_1 + r_2$
Ý nghĩa: Tổng hai góc khúc xạ trong lăng kính luôn bằng góc chiết quang A.
Ứng dụng: Biết A và $r_1$ thì tính được $r_2$ (hoặc ngược lại).
3. Công thức góc lệch
📌 Công thức tính góc lệch D:
$$\boxed{D = i_1 + i_2 – A}$$
Hoặc viết dưới dạng khác:
$$D = (i_1 – r_1) + (i_2 – r_2)$$
Chứng minh:
Từ hình học của đường đi tia sáng:
- Tại mặt AB: tia bị lệch một góc $(i_1 – r_1)$
- Tại mặt AC: tia bị lệch một góc $(i_2 – r_2)$
- Tổng góc lệch: $D = (i_1 – r_1) + (i_2 – r_2)$
- Biến đổi: $D = i_1 + i_2 – (r_1 + r_2) = i_1 + i_2 – A$
Ý nghĩa:
- $D > 0$: Tia ló luôn lệch về phía đáy lăng kính
- D phụ thuộc vào: góc tới $i_1$, chiết suất $n$, góc chiết quang $A$
- Khi thay đổi $i_1$, góc lệch D cũng thay đổi
4. Điều kiện để có tia ló ra khỏi lăng kính
Điều kiện cần thiết: Để có tia sáng ló ra khỏi mặt AC, góc tới $r_2$ phải nhỏ hơn góc tới giới hạn:
$$\boxed{r_2 < i_{gh}}$$
Công thức góc tới giới hạn:
$$\boxed{\sin i_{gh} = \frac{n_0}{n} = \frac{1}{n}}$$
(với môi trường ngoài là không khí, $n_0 = 1$)
Ý nghĩa:
- Nếu $r_2 < i_{gh}$: Có tia ló ra ngoài (khúc xạ bình thường)
- Nếu $r_2 = i_{gh}$: Tia ló là tiếp tuyến với mặt AC
- Nếu $r_2 > i_{gh}$: Xảy ra phản xạ toàn phần, không có tia ló
Ví dụ: Với lăng kính thủy tinh có $n = 1.5$: $$\sin i_{gh} = \frac{1}{1.5} = 0.667$$ $$i_{gh} = \arcsin(0.667) \approx 41.8°$$
Vậy để có tia ló: $r_2 < 41.8°$
5. Ví dụ minh họa tổng hợp
Bài toán: Một lăng kính có góc chiết quang $A = 60°$ và chiết suất $n = 1.5$. Một tia sáng đơn sắc tới mặt AB của lăng kính với góc tới $i_1 = 45°$.
a) Tính góc khúc xạ $r_1$ tại mặt AB
b) Tính góc tới $r_2$ tại mặt AC
c) Kiểm tra điều kiện có tia ló
d) Tính góc ló $i_2$
e) Tính góc lệch D
Lời giải:
Câu a) Tính $r_1$:
Áp dụng định luật khúc xạ tại mặt AB: $$\sin i_1 = n \sin r_1$$ $$\sin r_1 = \frac{\sin i_1}{n} = \frac{\sin 45°}{1.5}$$ $$\sin r_1 = \frac{0.707}{1.5} = 0.471$$ $$r_1 = \arcsin(0.471) \approx 28.1°$$
Câu b) Tính $r_2$:
Áp dụng công thức góc trong lăng kính: $$r_2 = A – r_1 = 60° – 28.1° = 31.9°$$
Câu c) Kiểm tra điều kiện có tia ló:
Tính góc tới giới hạn: $$\sin i_{gh} = \frac{1}{n} = \frac{1}{1.5} = 0.667$$ $$i_{gh} \approx 41.8°$$
So sánh: $r_2 = 31.9° < 41.8° = i_{gh}$
Kết luận: Có tia ló ra khỏi lăng kính ✓
Câu d) Tính $i_2$:
Áp dụng định luật khúc xạ tại mặt AC: $$n \sin r_2 = \sin i_2$$ $$\sin i_2 = n \sin r_2 = 1.5 \times \sin 31.9°$$ $$\sin i_2 = 1.5 \times 0.529 = 0.794$$ $$i_2 = \arcsin(0.794) \approx 52.5°$$
Câu e) Tính góc lệch D:
Áp dụng công thức góc lệch: $$D = i_1 + i_2 – A$$ $$D = 45° + 52.5° – 60° = 37.5°$$
Kết luận: Góc lệch là $D = 37.5°$ (tia ló lệch về phía đáy)
IV. TRƯỜNG HỢP LĂNG KÍNH GÓC NHỎ
1. Điều kiện góc nhỏ
Lăng kính góc nhỏ là trường hợp đặc biệt khi:
- Góc chiết quang A nhỏ: $A < 10°$ (hoặc $A < 15°$ theo một số tài liệu)
- Góc tới $i_1$ cũng nhỏ
Xấp xỉ góc nhỏ trong toán học:
Khi góc $\alpha$ nhỏ (đo bằng radian), ta có: $$\sin \alpha \approx \alpha$$ $$\tan \alpha \approx \alpha$$ $$\cos \alpha \approx 1$$
Lưu ý: Công thức xấp xỉ này chỉ chính xác khi góc đo bằng radian. Nếu góc đo bằng độ, cần đổi sang radian: $\alpha_{rad} = \alpha_{độ} \times \frac{\pi}{180}$
2. Công thức đơn giản cho lăng kính góc nhỏ
📌 Công thức góc trong (không đổi):
$$A \approx r_1 + r_2$$
(Công thức này vẫn đúng, không thay đổi)
📌 Công thức góc lệch đơn giản:
$$\boxed{D \approx (n – 1)A}$$
Chứng minh:
Xuất phát từ công thức khúc xạ:
- Tại mặt AB: $\sin i_1 = n \sin r_1$ → $i_1 \approx n r_1$ (góc nhỏ)
- Tại mặt AC: $n \sin r_2 = \sin i_2$ → $n r_2 \approx i_2$ (góc nhỏ)
Công thức góc lệch: $$D = i_1 + i_2 – A$$ $$D \approx n r_1 + n r_2 – A$$ $$D \approx n(r_1 + r_2) – A$$ $$D \approx nA – A$$ $$D \approx (n – 1)A$$
Ý nghĩa quan trọng:
- Góc lệch D tỉ lệ thuận với $(n – 1)$ và góc chiết quang A
- D không phụ thuộc vào góc tới $i_1$ (trong xấp xỉ góc nhỏ)
- Công thức rất đơn giản, dễ tính toán
3. Ví dụ về lăng kính góc nhỏ
Bài toán: Một lăng kính có góc chiết quang $A = 5° = 0.087$ rad và chiết suất $n = 1.6$. Tính góc lệch D.
Lời giải:
Phương pháp 1: Dùng công thức đơn giản (góc bằng độ) $$D \approx (n – 1)A = (1.6 – 1) \times 5° = 0.6 \times 5° = 3°$$
Phương pháp 2: Dùng công thức đơn giản (góc bằng radian) $$D \approx (n – 1)A = (1.6 – 1) \times 0.087 = 0.6 \times 0.087 = 0.052 \text{ rad}$$
Đổi sang độ: $D = 0.052 \times \frac{180}{\pi} \approx 2.98° \approx 3°$
Kết luận: Góc lệch $D \approx 3°$
4. Ứng dụng công thức góc nhỏ
Ứng dụng 1: Đo chiết suất
Từ công thức $D \approx (n – 1)A$, ta suy ra:
$$\boxed{n \approx 1 + \frac{D}{A}}$$
Phương pháp đo:
- Đo góc chiết quang A (bằng thước đo góc)
- Đo góc lệch D (bằng thực nghiệm với góc tới nhỏ)
- Tính chiết suất n theo công thức trên
Ví dụ: Lăng kính có $A = 8°$, đo được $D = 4°$. Tính n? $$n \approx 1 + \frac{4°}{8°} = 1 + 0.5 = 1.5$$
Ứng dụng 2: Thiết kế lăng kính
Khi cần một lăng kính có góc lệch D xác định, ta chọn:
$$\boxed{A \approx \frac{D}{n – 1}}$$
Ví dụ: Muốn góc lệch $D = 6°$, dùng thủy tinh có $n = 1.5$. Tính A? $$A \approx \frac{6°}{1.5 – 1} = \frac{6°}{0.5} = 12°$$
5. So sánh góc lớn và góc nhỏ
| Tiêu chí | Góc lớn | Góc nhỏ ($A < 10°$) |
|---|---|---|
| Công thức góc lệch | $D = i_1 + i_2 – A$ | $D \approx (n-1)A$ |
| Phụ thuộc $i_1$ | Có (phức tạp) | Không (gần đúng) |
| Độ chính xác | Chính xác | Xấp xỉ (sai số nhỏ) |
| Tính toán | Phức tạp, nhiều bước | Đơn giản, nhanh |
| Ứng dụng | Lăng kính chuẩn 60° | Đo chiết suất, thiết kế |
Khi nào dùng công thức góc nhỏ?
- A < 10°: Sai số < 1%
- A < 15°: Sai số < 2% (vẫn chấp nhận được)
- A > 15°: Nên dùng công thức chính xác
V. GÓC LỆCH CỰC TIỂU
1. Định nghĩa góc lệch cực tiểu
Góc lệch cực tiểu ($D_m$ hoặc $D_{min}$): Là giá trị nhỏ nhất của góc lệch D khi ta thay đổi góc tới $i_1$.
Hiện tượng quan sát:
- Khi tăng dần $i_1$ từ 0°, góc lệch D giảm
- D đạt giá trị nhỏ nhất $D_m$ tại một góc tới đặc biệt
- Sau đó, khi tiếp tục tăng $i_1$, góc D lại tăng
Điều kiện để D đạt cực tiểu:
$$\boxed{i_1 = i_2 \quad \text{và} \quad r_1 = r_2}$$
Ý nghĩa vật lý:
- Đường đi của tia sáng trong lăng kính đối xứng qua mặt phẳng phân giác của góc A
- Tia sáng truyền qua lăng kính theo đường “thuận lợi nhất”
2. Công thức góc lệch cực tiểu
📌 Khi D = $D_m$, ta có:
$$\boxed{r_1 = r_2 = \frac{A}{2}}$$
$$\boxed{i_1 = i_2 = i_m}$$
(ký hiệu $i_m$ là góc tới khi D cực tiểu)
📌 Công thức tính chiết suất từ $D_m$ và A:
$$\boxed{n = \frac{\sin\frac{A + D_m}{2}}{\sin\frac{A}{2}}}$$
Chứng minh:
Khi $D = D_m$, có $r_1 = r_2 = \frac{A}{2}$
Từ định luật khúc xạ tại mặt AB: $$\sin i_1 = n \sin r_1 = n \sin \frac{A}{2}$$
Từ công thức góc lệch: $$D_m = i_1 + i_2 – A = 2i_1 – A$$ (vì $i_1 = i_2$) $$i_1 = \frac{A + D_m}{2}$$
Thay vào: $$\sin \frac{A + D_m}{2} = n \sin \frac{A}{2}$$
$$\Rightarrow n = \frac{\sin\frac{A + D_m}{2}}{\sin\frac{A}{2}}$$
📌 Công thức tính $D_m$ từ n và A:
$$\sin\frac{A + D_m}{2} = n \sin\frac{A}{2}$$
$$D_m = 2\arcsin\left(n\sin\frac{A}{2}\right) – A$$
3. Ý nghĩa của góc lệch cực tiểu
Trong thực nghiệm:
- Góc lệch cực tiểu $D_m$ là giá trị dễ quan sát nhất (ổn định, không thay đổi nhanh khi xoay lăng kính)
- Dùng để đo chiết suất chính xác của lăng kính
Trong lý thuyết:
- Tại $D_m$, đường đi ánh sáng qua lăng kính đối xứng
- Đây là trạng thái “tối ưu” về mặt quang học
Ưu điểm phương pháp đo chiết suất bằng $D_m$:
- Chính xác cao (sai số nhỏ)
- Dễ thực hiện (tìm vị trí D nhỏ nhất)
- Không cần biết góc tới $i_1$ chính xác
4. Ví dụ tính góc lệch cực tiểu
Bài toán: Một lăng kính có góc chiết quang $A = 60°$ và chiết suất $n = 1.5$.
a) Tính góc lệch cực tiểu $D_m$
b) Tính góc tới $i_1$ khi D đạt cực tiểu
Lời giải:
Câu a) Tính $D_m$:
Áp dụng công thức: $$\sin\frac{A + D_m}{2} = n\sin\frac{A}{2}$$
Thay số: $$\sin\frac{60° + D_m}{2} = 1.5 \times \sin\frac{60°}{2}$$ $$\sin\frac{60° + D_m}{2} = 1.5 \times \sin 30°$$ $$\sin\frac{60° + D_m}{2} = 1.5 \times 0.5 = 0.75$$
Suy ra: $$\frac{60° + D_m}{2} = \arcsin(0.75) \approx 48.6°$$ $$60° + D_m = 97.2°$$ $$D_m = 97.2° – 60° = 37.2°$$
Câu b) Tính $i_1$:
Khi $D = D_m$: $$i_1 = \frac{A + D_m}{2} = \frac{60° + 37.2°}{2} = \frac{97.2°}{2} = 48.6°$$
Kết luận:
- Góc lệch cực tiểu: $D_m = 37.2°$
- Góc tới tương ứng: $i_1 = 48.6°$
VI. QUANG PHỔ VÀ TÁN SẮC ÁNH SÁNG
1. Hiện tượng tán sắc ánh sáng
Định nghĩa: Tán sắc ánh sáng là hiện tượng ánh sáng trắng (ánh sáng Mặt Trời, ánh sáng đèn sợi đốt) bị phân tách thành nhiều màu sắc khác nhau khi đi qua lăng kính.
Nguyên nhân:
- Chiết suất $n$ của chất làm lăng kính phụ thuộc vào bước sóng $\lambda$ của ánh sáng
- Mỗi màu sắc (tương ứng với một bước sóng) có chiết suất khác nhau
- Ánh sáng màu khác nhau bị lệch góc khác nhau
Quy luật:
- Ánh sáng tím: Bước sóng ngắn nhất → chiết suất lớn nhất ($n_{tím}$ lớn) → bị lệch nhiều nhất
- Ánh sáng đỏ: Bước sóng dài nhất → chiết suất nhỏ nhất ($n_{đỏ}$ nhỏ) → bị lệch ít nhất
Hệ quả: $$n_{tím} > n_{lam} > n_{chàm} > n_{lục} > n_{vàng} > n_{cam} > n_{đỏ}$$
$$D_{tím} > D_{lam} > D_{chàm} > D_{lục} > D_{vàng} > D_{cam} > D_{đỏ}$$
2. Quang phổ liên tục của ánh sáng trắng
Quang phổ: Dải màu thu được khi ánh sáng trắng đi qua lăng kính.
Thành phần 7 màu cơ bản (theo thứ tự từ ít lệch đến lệch nhiều):
Đỏ – Cam – Vàng – Lục – Lam – Chàm – Tím
(Có thể nhớ: Đừng Cóc Vì Làm Liệm Chó Tô – theo một số cách ghi nhớ)
Thứ tự độ lệch (từ ít đến nhiều): $$D_{đỏ} < D_{cam} < D_{vàng} < D_{lục} < D_{lam} < D_{chàm} < D_{tím}$$
Đặc điểm:
- Màu đỏ ở gần phía đỉnh lăng kính (lệch ít)
- Màu tím ở gần phía đáy lăng kính (lệch nhiều)
- Các màu chuyển đổi liên tục, không có ranh giới rõ ràng
3. Góc tán sắc
Định nghĩa: Góc tán sắc ($\delta$) là góc giữa tia màu đỏ và tia màu tím sau khi ló ra khỏi lăng kính.
$$\boxed{\delta = D_{tím} – D_{đỏ}}$$
Với lăng kính góc nhỏ:
Áp dụng công thức $D \approx (n – 1)A$ cho từng màu:
- $D_{tím} \approx (n_{tím} – 1)A$
- $D_{đỏ} \approx (n_{đỏ} – 1)A$
Góc tán sắc: $$\boxed{\delta \approx (n_{tím} – n_{đỏ})A}$$
Ý nghĩa:
- Góc tán sắc càng lớn, khả năng phân tách màu càng tốt
- $\delta$ tỉ lệ với hiệu chiết suất $(n_{tím} – n_{đỏ})$ và góc chiết quang A
Ví dụ: Lăng kính có $A = 10°$, $n_{đỏ} = 1.50$, $n_{tím} = 1.54$. Tính góc tán sắc?
$$\delta \approx (1.54 – 1.50) \times 10° = 0.04 \times 10° = 0.4°$$
4. Ứng dụng của tán sắc ánh sáng
Máy quang phổ lăng kính:
- Phân tích thành phần ánh sáng từ các nguồn (Mặt Trời, sao, ngọn lửa…)
- Xác định thành phần hóa học của các chất phát sáng
- Nghiên cứu cấu trúc nguyên tử và phân tử
Cầu vồng:
- Hiện tượng tán sắc ánh sáng Mặt Trời qua các giọt nước mưa
- Mỗi giọt nước đóng vai trò như một lăng kính nhỏ
- Cầu vồng có 7 màu theo thứ tự: Đỏ – Cam – Vàng – Lục – Lam – Chàm – Tím (từ ngoài vào trong)
Quang học sinh học:
- Phân tích mẫu máu, nước tiểu bằng quang phổ
- Chẩn đoán bệnh qua sự thay đổi quang phổ
Đo chiết suất theo bước sóng:
- Xác định đặc tính quang học của vật liệu
- Nghiên cứu tính chất vật liệu mới
VII. BẢNG CÔNG THỨC TỔNG HỢP
A. Công thức chính (quan trọng nhất)
| Tên công thức | Biểu thức | Ghi chú |
|---|---|---|
| Khúc xạ mặt AB | $\sin i_1 = n\sin r_1$ | Tia vào lăng kính |
| Khúc xạ mặt AC | $n\sin r_2 = \sin i_2$ | Tia ra khỏi lăng kính |
| Góc trong lăng kính | $A = r_1 + r_2$ | Tổng 2 góc khúc xạ trong |
| Góc lệch | $D = i_1 + i_2 – A$ | Góc lệch tổng quát |
B. Công thức lăng kính góc nhỏ
| Trường hợp | Công thức | Điều kiện |
|---|---|---|
| Góc lệch đơn giản | $D \approx (n-1)A$ | $A < 10°$ |
| Tính chiết suất | $n \approx 1 + \frac{D}{A}$ | Từ đo D và A |
| Góc tán sắc | $\delta \approx (n_{tím} – n_{đỏ})A$ | Tán sắc ánh sáng |
C. Công thức góc lệch cực tiểu
| Đại lượng | Công thức | Ý nghĩa |
|---|---|---|
| Điều kiện cực tiểu | $i_1 = i_2$, $r_1 = r_2 = \frac{A}{2}$ | Đường đi đối xứng |
| Tính chiết suất từ $D_m$ | $n = \frac{\sin\frac{A+D_m}{2}}{\sin\frac{A}{2}}$ | Đo n chính xác |
| Tính $D_m$ từ n | $D_m = 2\arcsin(n\sin\frac{A}{2}) – A$ | Thiết kế lăng kính |
D. Điều kiện tia ló và góc giới hạn
| Công thức | Biểu thức | Ý nghĩa |
|---|---|---|
| Góc tới giới hạn | $\sin i_{gh} = \frac{1}{n}$ | Từ lăng kính ra không khí |
| Điều kiện có tia ló | $r_2 < i_{gh}$ | Không phản xạ toàn phần |
| Giá trị $i_{gh}$ | $i_{gh} = \arcsin(\frac{1}{n})$ | Phụ thuộc chiết suất |
VIII. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Công thức góc trong lăng kính:
“A = tổng hai góc khúc xạ”
$$A = r_1 + r_2$$
Cách nhớ: Trong lăng kính, tổng hai góc khúc xạ luôn bằng góc chiết quang A.
Công thức góc lệch:
“D = tổng góc ngoài trừ góc trong”
$$D = i_1 + i_2 – A$$
Cách nhớ: Lấy tổng hai góc bên ngoài ($i_1$ và $i_2$) trừ đi góc bên trong (A).
Công thức góc nhỏ:
“D = hiệu chiết suất nhân góc A”
$$D \approx (n-1)A$$
Cách nhớ:
- $(n – 1)$ là hiệu giữa chiết suất lăng kính và không khí
- Nhân với góc chiết quang A
Công thức tán sắc:
“Tím lệch nhiều nhất, đỏ lệch ít nhất”
$$D_{tím} > D_{đỏ}$$ $$\delta = D_{tím} – D_{đỏ}$$
Cách nhớ: Màu tím có bước sóng ngắn, chiết suất lớn → lệch nhiều về phía đáy.
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm chiều góc lệch
Sai: Tia ló lệch về phía đỉnh lăng kính ❌
Đúng: Tia ló luôn lệch về phía đáy lăng kính ✓
❌ SAI LẦM 2: Quên điều kiện để có tia ló
Sai: Tia sáng luôn có tia ló ra khỏi lăng kính ❌
Đúng: Phải kiểm tra điều kiện $r_2 < i_{gh}$ ✓
Nếu $r_2 \geq i_{gh}$ → Phản xạ toàn phần, không có tia ló
❌ SAI LẦM 3: Dùng công thức góc nhỏ khi góc lớn
Sai: Áp dụng $D \approx (n-1)A$ với $A = 60°$ ❌
Đúng: Công thức góc nhỏ chỉ đúng khi $A < 10°$ (hoặc $< 15°$) ✓
❌ SAI LẦM 4: Nhầm thứ tự màu sắc trong quang phổ
Sai: Tím – Chàm – Lam – Lục – Vàng – Cam – Đỏ (ngược) ❌
Đúng: Đỏ – Cam – Vàng – Lục – Lam – Chàm – Tím (đúng thứ tự từ ít lệch đến lệch nhiều) ✓
❌ SAI LẦM 5: Quên đổi độ sang radian
Sai: Dùng $D \approx (n-1)A$ với A = 5° nhưng tính bằng radian ❌
Đúng: Nếu dùng radian, phải đổi: $A = 5° = 5 \times \frac{\pi}{180} \approx 0.087$ rad ✓
Hoặc tính trực tiếp bằng độ nếu công thức cho phép.
3. Kiểm tra kết quả
Kiểm tra 1: Góc lệch luôn dương
Tia sáng qua lăng kính luôn bị lệch về phía đáy: $$D > 0$$
Nếu tính ra $D < 0$ → Sai
Kiểm tra 2: Tổng góc trong
Luôn kiểm tra: $$A = r_1 + r_2$$
Nếu $r_1 + r_2 \neq A$ → Sai từ bước trước
Kiểm tra 3: So sánh góc khúc xạ
Khi ánh sáng đi từ không khí vào lăng kính: $$i_1 > r_1$$ (tia gập lại gần pháp tuyến)
Khi ánh sáng đi từ lăng kính ra không khí: $$i_2 > r_2$$ (tia bẻ ra xa pháp tuyến)
Kiểm tra 4: Điều kiện có tia ló
Luôn kiểm tra: $$r_2 < i_{gh} = \arcsin\left(\frac{1}{n}\right)$$
Nếu $r_2 \geq i_{gh}$ → Không có tia ló (phản xạ toàn phần)
IX. BÀI TẬP MẪU
Bài tập 1: Tính góc khúc xạ
Đề bài: Một lăng kính thủy tinh có chiết suất $n = 1.5$. Một tia sáng tới mặt AB của lăng kính với góc tới $i_1 = 60°$. Tính góc khúc xạ $r_1$ tại mặt AB.
Lời giải:
Áp dụng định luật khúc xạ tại mặt AB: $$\sin i_1 = n \sin r_1$$
$$\sin r_1 = \frac{\sin i_1}{n} = \frac{\sin 60°}{1.5}$$
$$\sin r_1 = \frac{0.866}{1.5} = 0.577$$
$$r_1 = \arcsin(0.577) \approx 35.3°$$
Đáp số: $r_1 \approx 35.3°$
Bài tập 2: Tính góc lệch
Đề bài: Lăng kính có góc chiết quang $A = 60°$. Tia sáng tới với góc tới $i_1 = 45°$ và ló ra với góc ló $i_2 = 50°$. Tính góc lệch D.
Lời giải:
Áp dụng công thức góc lệch: $$D = i_1 + i_2 – A$$
$$D = 45° + 50° – 60° = 35°$$
Đáp số: $D = 35°$
Nhận xét: $D > 0$ → Tia ló lệch về phía đáy ✓
Bài tập 3: Lăng kính góc nhỏ
Đề bài: Một lăng kính có góc chiết quang $A = 8°$ và chiết suất $n = 1.52$. Tính góc lệch D (dùng công thức góc nhỏ).
Lời giải:
Vì $A = 8° < 10°$, ta dùng công thức góc nhỏ: $$D \approx (n – 1)A$$
$$D \approx (1.52 – 1) \times 8°$$
$$D \approx 0.52 \times 8° = 4.16°$$
Đáp số: $D \approx 4.16°$
Bài tập 4: Đo chiết suất bằng góc lệch cực tiểu
Đề bài: Một lăng kính có góc chiết quang $A = 60°$. Đo được góc lệch cực tiểu $D_m = 40°$. Tính chiết suất n của lăng kính.
Lời giải:
Áp dụng công thức góc lệch cực tiểu: $$n = \frac{\sin\frac{A + D_m}{2}}{\sin\frac{A}{2}}$$
$$n = \frac{\sin\frac{60° + 40°}{2}}{\sin\frac{60°}{2}}$$
$$n = \frac{\sin 50°}{\sin 30°}$$
$$n = \frac{0.766}{0.5} = 1.532$$
Đáp số: $n \approx 1.532$
Bài tập 5: Tính góc tới giới hạn
Đề bài: Lăng kính có chiết suất $n = 1.6$. Tính góc tới giới hạn $i_{gh}$ để tia sáng có thể ló ra khỏi lăng kính.
Lời giải:
Áp dụng công thức góc tới giới hạn: $$\sin i_{gh} = \frac{1}{n}$$
$$\sin i_{gh} = \frac{1}{1.6} = 0.625$$
$$i_{gh} = \arcsin(0.625) \approx 38.7°$$
Đáp số: $i_{gh} \approx 38.7°$
Ý nghĩa: Để có tia ló, góc tới $r_2$ tại mặt AC phải nhỏ hơn $38.7°$.
Bài tập 6: Kiểm tra điều kiện tia ló
Đề bài: Lăng kính có $n = 1.5$ và $A = 60°$. Tia sáng khúc xạ vào lăng kính với góc $r_1 = 20°$. Hỏi có tia ló ra khỏi lăng kính không?
Lời giải:
Bước 1: Tính $r_2$ $$r_2 = A – r_1 = 60° – 20° = 40°$$
Bước 2: Tính góc tới giới hạn $$\sin i_{gh} = \frac{1}{n} = \frac{1}{1.5} = 0.667$$ $$i_{gh} = \arcsin(0.667) \approx 41.8°$$
Bước 3: So sánh $r_2$ và $i_{gh}$ $$r_2 = 40° < i_{gh} = 41.8°$$
Kết luận: Vì $r_2 < i_{gh}$, nên có tia ló ra khỏi lăng kính ✓
X. KẾT LUẬN
Tổng kết
Bài viết đã trình bày đầy đủ và chi tiết các công thức lăng kính cho chương trình Vật lý lớp 11:
4 công thức cơ bản:
- Khúc xạ mặt AB: $\sin i_1 = n\sin r_1$
- Khúc xạ mặt AC: $n\sin r_2 = \sin i_2$
- Góc trong: $A = r_1 + r_2$
- Góc lệch: $D = i_1 + i_2 – A$
Công thức góc nhỏ (quan trọng): $$D \approx (n-1)A$$
Công thức góc lệch cực tiểu: $$n = \frac{\sin\frac{A+D_m}{2}}{\sin\frac{A}{2}}$$
Điều kiện tia ló: $$r_2 < i_{gh}, \quad \sin i_{gh} = \frac{1}{n}$$
Tán sắc ánh sáng:
- 7 màu: Đỏ – Cam – Vàng – Lục – Lam – Chàm – Tím
- Góc tán sắc: $\delta = D_{tím} – D_{đỏ} \approx (n_{tím} – n_{đỏ})A$
Lời khuyên học tập
📌 Học thuộc 3 công thức chính – Đây là nền tảng để giải mọi bài tập
📌 Nhớ quy tắc: Tia sáng luôn lệch về phía đáy lăng kính
📌 Công thức góc nhỏ chỉ dùng khi $A < 10°$ (hoặc $< 15°$) – Không áp dụng cho lăng kính góc lớn
📌 Tán sắc: Nhớ thứ tự 7 màu và quy tắc “Tím lệch nhiều, đỏ lệch ít”
📌 Kiểm tra điều kiện tia ló: Luôn so sánh $r_2$ với $i_{gh}$ trước khi tính $i_2$
📌 Vẽ hình: Vẽ sơ đồ đường đi tia sáng giúp hình dung rõ hơn và tránh nhầm lẫn
📌 Làm nhiều bài tập: Luyện tập là cách tốt nhất để nắm vững công thức và phương pháp giải

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
