Chọn đến phần học sinh cần nhanh chóng thông qua mục lục bằng cách click đến phần đó
- I. GIỚI THIỆU VỀ GIAO THOA SÓNG
- 1. Giao thoa sóng là gì?
- 2. Phân loại giao thoa sóng
- 3. Đặc điểm chung của giao thoa
- II. GIAO THOA SÓNG CƠ (SÓNG MẶT NƯỚC)
- 1. Điều kiện giao thoa sóng cơ
- 2. Hiệu đường đi
- 3. Điều kiện cực đại (dao động mạnh)
- 4. Điều kiện cực tiểu (dao động yếu)
- 5. Số cực đại và cực tiểu trên đoạn nối hai nguồn
- 6. Khoảng cách giữa hai cực đại (hoặc cực tiểu) liên tiếp
- III. GIAO THOA ÁNH SÁNG – THÍ NGHIỆM YOUNG
- 1. Sơ đồ thí nghiệm Young (Thí nghiệm khe Y-âng)
- 2. Vị trí vân sáng
- 3. Vị trí vân tối
- 4. Khoảng vân (i) – CÔNG THỨC QUAN TRỌNG NHẤT
- 5. Số vân sáng và vân tối trên màn
- 6. Bước sóng ánh sáng đơn sắc
- 7. Bảng bước sóng và màu sắc ánh sáng
- IV. BẢNG CÔNG THỨC TỔNG HỢP
- A. Giao thoa sóng cơ
- B. Giao thoa ánh sáng (Thí nghiệm Young)
- C. Liên hệ các đại lượng trong giao thoa ánh sáng
- V. PHÂN BIỆT GIAO THOA SÓNG CƠ VÀ ÁNH SÁNG
- VI. MẸO VÀ LƯU Ý
- 1. Mẹo nhớ công thức
- 2. Các sai lầm thường gặp
- 3. Quy trình giải bài tập nhanh (4 BƯỚC)
- VII. BÀI TẬP MẪU
- VIII. ỨNG DỤNG THỰC TẾ
- IX. KẾT LUẬN
- Nguyên lý cơ bản cần nắm vững
- Lời khuyên học tập
I. GIỚI THIỆU VỀ GIAO THOA SÓNG
1. Giao thoa sóng là gì?
Định nghĩa: Giao thoa sóng là hiện tượng xảy ra khi hai sóng kết hợp gặp nhau, chồng chất lên nhau tạo ra những vùng dao động cực đại (dao động mạnh) và những vùng dao động cực tiểu (dao động yếu hoặc đứng yên).
Đặc điểm của hiện tượng giao thoa:
Vùng cực đại (dao động mạnh): Là những vùng mà hai sóng gặp nhau cùng pha, tăng cường lẫn nhau, tạo biên độ dao động cực đại. Trên mặt nước, đây là những vùng dao động mạnh. Với ánh sáng, đây là những vân sáng.
Vùng cực tiểu (dao động yếu): Là những vùng mà hai sóng gặp nhau ngược pha, triệt tiêu lẫn nhau, tạo biên độ dao động cực tiểu (có thể bằng 0). Trên mặt nước, đây là những vùng đứng yên hoặc dao động yếu. Với ánh sáng, đây là những vân tối.
Điều kiện để có giao thoa: Hai nguồn sóng phải là nguồn kết hợp, tức là:
- Cùng tần số (cùng chu kỳ T, cùng bước sóng λ)
- Độ lệch pha không đổi theo thời gian (cùng pha hoặc lệch pha một lượng cố định)
Nếu không thỏa mãn điều kiện này: Sóng chỉ chồng chất hỗn loạn, không tạo vùng cực đại và cực tiểu ổn định.
2. Phân loại giao thoa sóng
| Loại giao thoa | Môi trường truyền | Ví dụ thực tế |
|---|---|---|
| Giao thoa sóng cơ | Mặt nước, dây, không khí (âm thanh) | Hai nguồn dao động trên mặt nước tạo hoa văn giao thoa |
| Giao thoa ánh sáng | Chân không, không khí, thủy tinh, môi trường trong suốt | Thí nghiệm Young (khe Y-âng), màu sắc trên bong bóng xà phòng |
Sự khác biệt:
- Sóng cơ: Quan sát trực tiếp dao động mạnh/yếu
- Ánh sáng: Quan sát các vân sáng/tối trên màn
3. Đặc điểm chung của giao thoa
Xuất hiện vân (hoặc vùng) xen kẽ:
- Vân sáng (cực đại) và vân tối (cực tiểu) xen kẽ nhau
- Hoặc vùng dao động mạnh và yếu xen kẽ nhau
Tính đối xứng:
- Các vân/vùng phân bố đối xứng qua trục nối hai nguồn
- Vân trung tâm (k = 0) nằm ở vị trí đối xứng
Khoảng cách đều đặn:
- Khoảng cách giữa các vân liên tiếp bằng nhau (gọi là khoảng vân i)
- Khoảng cách giữa các cực đại (hoặc cực tiểu) liên tiếp không đổi
II. GIAO THOA SÓNG CƠ (SÓNG MẶT NƯỚC)
1. Điều kiện giao thoa sóng cơ
Để có hiện tượng giao thoa ổn định, hai nguồn sóng $S_1$ và $S_2$ phải là nguồn kết hợp:
Điều kiện 1: Cùng tần số
- Hai nguồn dao động với cùng tần số $f$ (hoặc cùng chu kỳ $T = \frac{1}{f}$)
- Cùng bước sóng $\lambda = \frac{v}{f}$ (với v là vận tốc sóng)
Điều kiện 2: Độ lệch pha không đổi
- Hai nguồn dao động cùng pha (lệch pha 0)
- Hoặc lệch pha một góc cố định không thay đổi theo thời gian
Nếu không thỏa mãn: Giao thoa không ổn định, các vùng cực đại/cực tiểu thay đổi liên tục, không quan sát được.
2. Hiệu đường đi
Định nghĩa: Hiệu đường đi là độ chênh lệch khoảng cách từ hai nguồn đến một điểm M bất kỳ.
Công thức:
$$\boxed{d = |d_1 – d_2| = |MS_1 – MS_2|}$$
Trong đó:
- $d$: hiệu đường đi (m)
- $d_1 = MS_1$: khoảng cách từ điểm M đến nguồn $S_1$ (m)
- $d_2 = MS_2$: khoảng cách từ điểm M đến nguồn $S_2$ (m)
Ý nghĩa vật lý: Hiệu đường đi quyết định độ lệch pha giữa hai sóng tại M, từ đó xác định M nằm ở cực đại hay cực tiểu.
Lưu ý:
- Hiệu đường đi luôn lấy giá trị tuyệt đối
- Đơn vị phải cùng hệ với bước sóng λ
3. Điều kiện cực đại (dao động mạnh)
Tại điểm M dao động với biên độ cực đại khi:
$$\boxed{d = k\lambda \quad (k \in \mathbb{Z})}$$
Hoặc viết đầy đủ:
$$|d_1 – d_2| = k\lambda$$
Trong đó:
- $k = 0, \pm1, \pm2, \pm3, …$ (số nguyên, gọi là bậc của cực đại)
- $\lambda$: bước sóng (m)
Ý nghĩa: Hiệu đường đi bằng số nguyên lần bước sóng → hai sóng đến M cùng pha → tăng cường lẫn nhau → dao động mạnh.
Các trường hợp:
- $k = 0$: Cực đại trung tâm (đối xứng, nằm trên đường trung trực của $S_1S_2$)
- $k = 1, -1$: Cực đại bậc 1
- $k = 2, -2$: Cực đại bậc 2
- …
4. Điều kiện cực tiểu (dao động yếu)
Tại điểm M dao động với biên độ cực tiểu (hoặc đứng yên) khi:
$$\boxed{d = \left(k + \frac{1}{2}\right)\lambda \quad (k \in \mathbb{Z})}$$
Hoặc viết:
$$|d_1 – d_2| = (2k + 1)\frac{\lambda}{2}$$
Trong đó:
- $k = 0, \pm1, \pm2, \pm3, …$ (số nguyên)
- $\lambda$: bước sóng (m)
Ý nghĩa: Hiệu đường đi bằng số lẻ nửa bước sóng → hai sóng đến M ngược pha → triệt tiêu lẫn nhau → dao động yếu hoặc đứng yên.
Các trường hợp:
- $k = 0$: $d = \frac{\lambda}{2}$ (cực tiểu bậc 1)
- $k = 1$: $d = \frac{3\lambda}{2}$ (cực tiểu bậc 2)
- $k = -1$: $d = -\frac{\lambda}{2}$ (giá trị tuyệt đối = $\frac{\lambda}{2}$)
5. Số cực đại và cực tiểu trên đoạn nối hai nguồn
Trên đoạn thẳng nối hai nguồn $S_1S_2$ có độ dài $L$, số cực đại và cực tiểu được xác định bởi:
Số cực đại:
Giải bất phương trình: $$-\frac{L}{\lambda} \leq k \leq \frac{L}{\lambda}$$
Đếm số giá trị $k$ nguyên thỏa mãn.
Số cực tiểu:
Giải bất phương trình: $$-\frac{L}{\lambda} \leq k + 0.5 \leq \frac{L}{\lambda}$$
Hoặc: $$-\frac{L}{\lambda} – 0.5 \leq k \leq \frac{L}{\lambda} – 0.5$$
Đếm số giá trị $k$ nguyên thỏa mãn.
Ví dụ: Hai nguồn cách nhau $L = 10$ cm, bước sóng $\lambda = 2$ cm. Tính số cực đại trên đoạn $S_1S_2$.
Lời giải:
Điều kiện cực đại: $$-\frac{10}{2} \leq k \leq \frac{10}{2}$$ $$-5 \leq k \leq 5$$
Các giá trị k nguyên: $k = -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5$
Đếm: 11 giá trị
Kết luận: Có 11 cực đại trên đoạn nối hai nguồn.
6. Khoảng cách giữa hai cực đại (hoặc cực tiểu) liên tiếp
Trên đường vuông góc với $S_1S_2$ đi qua trung điểm O, khoảng cách giữa hai cực đại (hoặc cực tiểu) liên tiếp được tính gần đúng:
$$\boxed{\Delta x \approx \frac{\lambda D}{L}}$$
Trong đó:
- $\Delta x$: khoảng cách giữa hai cực đại (hoặc cực tiểu) liên tiếp
- $\lambda$: bước sóng
- $D$: khoảng cách từ điểm khảo sát đến trung điểm hai nguồn
- $L$: khoảng cách giữa hai nguồn $S_1S_2$
Lưu ý: Công thức này chỉ đúng với xấp xỉ khi $D >> L$ (điểm khảo sát xa hai nguồn).
III. GIAO THOA ÁNH SÁNG – THÍ NGHIỆM YOUNG
1. Sơ đồ thí nghiệm Young (Thí nghiệm khe Y-âng)
Bố trí thí nghiệm:
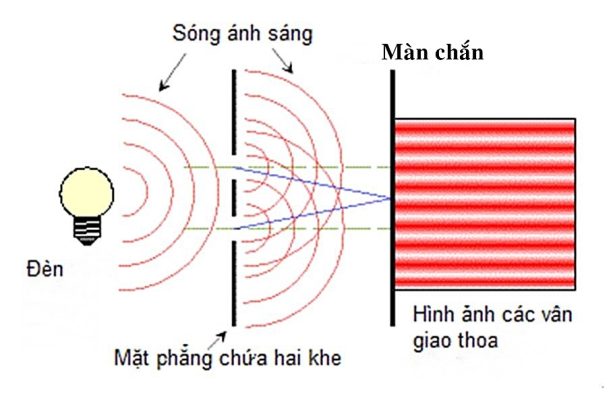
Các thành phần:
- S: Nguồn sáng đơn sắc (một màu, một bước sóng λ)
- F: Khe hẹp để tạo nguồn sáng kết hợp
- $S_1$, $S_2$: Hai khe hẹp song song, cách nhau khoảng $a$ (gọi là khoảng cách giữa hai khe)
- E: Màn quan sát đặt song song với mặt phẳng chứa hai khe, cách hai khe một khoảng $D$
- O: Điểm chính giữa màn, cách đều hai khe (vân sáng trung tâm)
Hiện tượng quan sát: Trên màn E xuất hiện các vân sáng và vân tối xen kẽ đều đặn, đối xứng qua O.
2. Vị trí vân sáng
Vân sáng (cực đại) xuất hiện tại những điểm M trên màn thỏa mãn:
$$\boxed{x = k\frac{\lambda D}{a} \quad (k \in \mathbb{Z})}$$
Hoặc viết theo khoảng vân:
$$x = ki$$
Trong đó:
- $x$: khoảng cách từ điểm M đến vân trung tâm O (có thể dương hoặc âm)
- $k = 0, \pm1, \pm2, \pm3, …$ (bậc của vân sáng)
- $k = 0$: Vân sáng trung tâm (vân sáng chính giữa, tại O)
- $k = 1, -1$: Vân sáng bậc 1 (hai bên vân trung tâm)
- $k = 2, -2$: Vân sáng bậc 2
- …
- $\lambda$: bước sóng ánh sáng (m)
- $D$: khoảng cách từ hai khe đến màn (m)
- $a$: khoảng cách giữa hai khe (m)
- $i = \frac{\lambda D}{a}$: khoảng vân
Lưu ý:
- Vân trung tâm ($k = 0$) luôn là vân sáng, nằm tại vị trí $x = 0$
- Các vân sáng phân bố đối xứng qua vân trung tâm
3. Vị trí vân tối
Vân tối (cực tiểu) xuất hiện tại những điểm M trên màn thỏa mãn:
$$\boxed{x = \left(k + \frac{1}{2}\right)\frac{\lambda D}{a} \quad (k \in \mathbb{Z})}$$
Hoặc:
$$x = (2k + 1)\frac{\lambda D}{2a}$$
Hoặc viết theo khoảng vân:
$$x = \left(k + \frac{1}{2}\right)i$$
Trong đó:
- $k = 0, \pm1, \pm2, \pm3, …$ (số nguyên)
Các vân tối:
- $k = 0$: Vân tối thứ nhất ($x = \frac{\lambda D}{2a} = \frac{i}{2}$)
- $k = 1$: Vân tối thứ hai ($x = \frac{3\lambda D}{2a} = \frac{3i}{2}$)
- …
Đặc điểm: Các vân tối nằm xen kẽ giữa các vân sáng.
4. Khoảng vân (i) – CÔNG THỨC QUAN TRỌNG NHẤT
Định nghĩa: Khoảng vân là khoảng cách giữa hai vân sáng liên tiếp (hoặc hai vân tối liên tiếp).
Công thức:
$$\boxed{i = \frac{\lambda D}{a}}$$
ĐÂY LÀ CÔNG THỨC CỐT LÕI CỦA GIAO THOA ÁNH SÁNG!
Trong đó:
- $i$: khoảng vân (m, cm, mm)
- $\lambda$: bước sóng ánh sáng (m)
- $D$: khoảng cách từ hai khe đến màn (m)
- $a$: khoảng cách giữa hai khe (m)
Ý nghĩa:
- Khoảng vân đặc trưng cho mức độ phân tán của vân giao thoa
- $i$ tỉ lệ thuận với $\lambda$ và $D$, tỉ lệ nghịch với $a$
- Bước sóng càng lớn → khoảng vân càng lớn
- Hai khe càng gần nhau → khoảng vân càng lớn
Từ công thức khoảng vân, ta có:
- Vị trí vân sáng bậc k: $x_k = ki$ (k = 0, ±1, ±2, …)
- Vị trí vân tối: $x_k = (k + 0.5)i$ (k = 0, ±1, ±2, …)
5. Số vân sáng và vân tối trên màn
Trên đoạn MN có độ dài L đối xứng qua vân trung tâm O:
Số vân sáng:
Điều kiện: $|x| \leq \frac{L}{2}$ và $x = ki$
$$|k| \leq \frac{L}{2i}$$
Số vân sáng một bên: $k_{max} = \left[\frac{L}{2i}\right]$ (phần nguyên)
Tổng số vân sáng: $$n_{sáng} = 2\left[\frac{L}{2i}\right] + 1$$
(Cộng 1 để tính cả vân trung tâm)
Số vân tối:
Điều kiện: $|x| \leq \frac{L}{2}$ và $x = (k + 0.5)i$
$$|k + 0.5| \leq \frac{L}{2i}$$
Tổng số vân tối: $$n_{tối} = 2\left[\frac{L}{2i} + 0.5\right]$$
Hoặc đơn giản: $n_{tối} = n_{sáng}$ hoặc $n_{tối} = n_{sáng} – 1$ (tùy trường hợp)
6. Bước sóng ánh sáng đơn sắc
Từ công thức khoảng vân, suy ra bước sóng:
$$\boxed{\lambda = \frac{ia}{D}}$$
Ứng dụng: Đây là phương pháp đo bước sóng ánh sáng chính xác trong phòng thí nghiệm.
Quy trình đo:
- Đo khoảng vân $i$ (bằng cách đo khoảng cách giữa nhiều vân rồi chia trung bình)
- Đo khoảng cách $a$ giữa hai khe
- Đo khoảng cách $D$ từ hai khe đến màn
- Tính $\lambda = \frac{ia}{D}$
7. Bảng bước sóng và màu sắc ánh sáng
| Màu sắc | Bước sóng λ (nm) | Bước sóng λ (m) |
|---|---|---|
| Đỏ | 640 – 760 | $(6.4 – 7.6) \times 10^{-7}$ |
| Cam | 590 – 640 | $(5.9 – 6.4) \times 10^{-7}$ |
| Vàng | 570 – 590 | $(5.7 – 5.9) \times 10^{-7}$ |
| Lục (xanh lá) | 500 – 570 | $(5.0 – 5.7) \times 10^{-7}$ |
| Lam | 460 – 500 | $(4.6 – 5.0) \times 10^{-7}$ |
| Chàm | 440 – 460 | $(4.4 – 4.6) \times 10^{-7}$ |
| Tím | 380 – 440 | $(3.8 – 4.4) \times 10^{-7}$ |
Lưu ý đổi đơn vị:
- $1 \text{ nm} = 10^{-9} \text{ m}$
- $1 \text{ μm} = 10^{-6} \text{ m} = 1000 \text{ nm}$
Ghi nhớ: Ánh sáng đỏ có bước sóng dài nhất, ánh sáng tím có bước sóng ngắn nhất.
IV. BẢNG CÔNG THỨC TỔNG HỢP
A. Giao thoa sóng cơ
| Đại lượng | Công thức | Điều kiện/Ghi chú |
|---|---|---|
| Hiệu đường đi | $d = |d_1 – d_2|$ | |
| Điều kiện cực đại | $d = k\lambda$ | $k = 0, \pm1, \pm2, …$ |
| Điều kiện cực tiểu | $d = (k+0.5)\lambda$ | $k = 0, \pm1, \pm2, …$ |
| Số cực đại trên $S_1S_2$ | $-\frac{L}{\lambda} \leq k \leq \frac{L}{\lambda}$ | Đếm số k nguyên |
| Khoảng cách cực đại liên tiếp | $\Delta x \approx \frac{\lambda D}{L}$ | Xấp xỉ khi D >> L |
B. Giao thoa ánh sáng (Thí nghiệm Young)
| Đại lượng | Công thức | Ghi chú |
|---|---|---|
| Khoảng vân ⭐ | $i = \frac{\lambda D}{a}$ | Quan trọng nhất |
| Vị trí vân sáng | $x = k\frac{\lambda D}{a} = ki$ | $k = 0, \pm1, \pm2, …$ |
| Vị trí vân tối | $x = (k+0.5)\frac{\lambda D}{a} = (k+0.5)i$ | $k = 0, \pm1, \pm2, …$ |
| Bước sóng | $\lambda = \frac{ia}{D}$ | Suy từ khoảng vân |
| Số vân sáng trên L | $n_{sáng} = 2\left[\frac{L}{2i}\right] + 1$ | L đối xứng qua O |
| Số vân tối trên L | $n_{tối} = 2\left[\frac{L}{2i} + 0.5\right]$ |
C. Liên hệ các đại lượng trong giao thoa ánh sáng
Từ công thức cốt lõi $i = \frac{\lambda D}{a}$, ta có thể suy ra:
$$\lambda = \frac{ia}{D}, \quad D = \frac{ia}{\lambda}, \quad a = \frac{\lambda D}{i}$$
Ứng dụng: Biết 3 trong 4 đại lượng ($i, \lambda, D, a$) → tính đại lượng còn lại.
V. PHÂN BIỆT GIAO THOA SÓNG CƠ VÀ ÁNH SÁNG
| Tiêu chí | Giao thoa sóng cơ | Giao thoa ánh sáng |
|---|---|---|
| Môi trường | Mặt nước, không khí, dây | Chân không, không khí, môi trường trong suốt |
| Đại lượng chính | Hiệu đường đi $d$ | Khoảng vân $i$ |
| Điều kiện cực đại | $d = k\lambda$ | $x = ki = k\frac{\lambda D}{a}$ |
| Điều kiện cực tiểu | $d = (k+0.5)\lambda$ | $x = (k+0.5)i$ |
| Quan sát | Dao động mạnh/yếu trên mặt nước | Vân sáng/vân tối trên màn |
| Ứng dụng | Âm thanh, sóng địa chấn | Quang học, đo bước sóng, giao thoa kế |
| Tần số | Thấp (Hz – kHz) | Rất cao ($10^{14}$ – $10^{15}$ Hz) |
Điểm giống nhau:
Đều cần nguồn kết hợp (cùng tần số, độ lệch pha không đổi)
Cực đại: hiệu đường đi = số nguyên lần λ
Cực tiểu: hiệu đường đi = số lẻ nửa λ
Hiện tượng có tính đối xứng
Khoảng cách giữa các vân/vùng liên tiếp đều đặn
VI. MẸO VÀ LƯU Ý
1. Mẹo nhớ công thức
Mẹo 1: Công thức cốt lõi giao thoa ánh sáng
$$\boxed{i = \frac{\lambda D}{a}}$$
Cách nhớ: “i đi trên a” → $i = \frac{…D}{a}$ (còn thiếu $\lambda$)
Hoặc: “Khoảng vân i tỉ lệ thuận với bước sóng λ và khoảng cách D, tỉ lệ nghịch với khoảng cách hai khe a”
Mẹo 2: Vân sáng – Vân tối
Vân sáng: k nguyên (0, 1, 2, 3, …) $$x = ki$$
Vân tối: k + 0.5 (nửa số nguyên) $$x = (k + 0.5)i$$
Cách nhớ:
- Sáng “tròn” → k nguyên
- Tối “lẻ” → k + 0.5
Mẹo 3: Điều kiện cực đại/cực tiểu
Cực đại (sáng): $d = k\lambda$ → nguyên lần bước sóng
Cực tiểu (tối): $d = (k + 0.5)\lambda$ → lẻ nửa lần bước sóng
Cách nhớ:
- Cùng pha (cực đại) → hiệu đường đi nguyên lần λ
- Ngược pha (cực tiểu) → hiệu đường đi lẻ nửa λ
2. Các sai lầm thường gặp
❌ SAI LẦM 1: Nhầm công thức sóng cơ và ánh sáng
Sai: Dùng $d = k\lambda$ cho giao thoa ánh sáng ❌
Đúng: Giao thoa ánh sáng dùng $x = ki = k\frac{\lambda D}{a}$ ✓
❌ SAI LẦM 2: Quên đổi đơn vị
Sai: Bước sóng λ = 600 nm, không đổi sang m khi tính ❌
Đúng:
- $\lambda = 600 \text{ nm} = 600 \times 10^{-9} \text{ m} = 6 \times 10^{-7} \text{ m}$ ✓
- Phải đổi tất cả về cùng đơn vị (thường là m hoặc cm)
❌ SAI LẦM 3: Nhầm vị trí vân sáng và vân tối
Sai: Vân sáng ở $x = (k + 0.5)i$ ❌
Đúng:
- Vân sáng: $x = ki$ (k nguyên) ✓
- Vân tối: $x = (k + 0.5)i$ (k + 0.5) ✓
❌ SAI LẦM 4: Quên k = 0 là vân trung tâm
Sai: Vân trung tâm là vân tối ❌
Đúng: Vân trung tâm (k = 0) LUÔN là vân sáng ✓
3. Quy trình giải bài tập nhanh (4 BƯỚC)
Bước 1: Xác định loại bài toán
- Giao thoa sóng cơ hay giao thoa ánh sáng?
- Tìm đại lượng nào: i, λ, vị trí vân, số vân, …?
Bước 2: Đổi tất cả về cùng đơn vị
- Bước sóng: nm → m
- Khoảng cách: mm → m hoặc cm
- Đảm bảo λ, a, D, i cùng đơn vị
Bước 3: Áp dụng công thức phù hợp
- Sóng cơ: Tính hiệu đường đi $d$, dùng $d = k\lambda$ hoặc $(k+0.5)\lambda$
- Ánh sáng: Tính khoảng vân $i = \frac{\lambda D}{a}$, rồi tính vị trí $x = ki$
Bước 4: Kiểm tra kết quả
- Đơn vị có hợp lý không?
- Vân sáng/tối có đúng với k đã cho không?
- Kết quả có hợp lý với đề bài không?
VII. BÀI TẬP MẪU
Bài tập 1: Giao thoa sóng cơ – Tìm số cực đại
Đề bài: Hai nguồn sóng kết hợp trên mặt nước cách nhau 10 cm, phát sóng có bước sóng 2 cm. Tìm số điểm dao động cực đại trên đoạn thẳng nối hai nguồn.
Lời giải:
Điều kiện cực đại trên đoạn $S_1S_2$: $$-\frac{L}{\lambda} \leq k \leq \frac{L}{\lambda}$$
Thay số: $$-\frac{10}{2} \leq k \leq \frac{10}{2}$$ $$-5 \leq k \leq 5$$
Các giá trị k nguyên thỏa mãn: $k = -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5$
Đếm: 11 giá trị
Đáp số: Có 11 điểm dao động cực đại trên đoạn nối hai nguồn.
Bài tập 2: Tính khoảng vân
Đề bài: Trong thí nghiệm Young về giao thoa ánh sáng, sử dụng ánh sáng đơn sắc có bước sóng $\lambda = 0.6 \text{ μm}$, khoảng cách giữa hai khe $a = 1 \text{ mm}$, khoảng cách từ hai khe đến màn $D = 2 \text{ m}$. Tính khoảng vân.
Lời giải:
Bước 1: Đổi đơn vị
- $\lambda = 0.6 \text{ μm} = 0.6 \times 10^{-6} \text{ m} = 6 \times 10^{-7} \text{ m}$
- $a = 1 \text{ mm} = 10^{-3} \text{ m}$
- $D = 2 \text{ m}$
Bước 2: Áp dụng công thức $$i = \frac{\lambda D}{a} = \frac{6 \times 10^{-7} \times 2}{10^{-3}}$$ $$= \frac{12 \times 10^{-7}}{10^{-3}} = 12 \times 10^{-4} \text{ m}$$ $$= 1.2 \times 10^{-3} \text{ m} = 1.2 \text{ mm}$$
Đáp số: Khoảng vân $i = 1.2 \text{ mm}$
Bài tập 3: Tính vị trí vân sáng
Đề bài: Trong thí nghiệm Young, khoảng vân đo được $i = 0.5 \text{ mm}$. Tính vị trí vân sáng bậc 3 so với vân trung tâm.
Lời giải:
Vị trí vân sáng bậc k: $$x = ki$$
Với k = 3: $$x_3 = 3 \times 0.5 = 1.5 \text{ mm}$$
Đáp số: Vân sáng bậc 3 cách vân trung tâm 1.5 mm.
Bài tập 4: Tính bước sóng
Đề bài: Trong thí nghiệm Young, khoảng cách giữa hai khe $a = 0.5 \text{ mm}$, khoảng cách từ hai khe đến màn $D = 1 \text{ m}$. Đo được khoảng vân $i = 1 \text{ mm}$. Tính bước sóng ánh sáng và cho biết ánh sáng có màu gì?
Lời giải:
Bước 1: Đổi đơn vị
- $a = 0.5 \text{ mm} = 0.5 \times 10^{-3} \text{ m}$
- $D = 1 \text{ m}$
- $i = 1 \text{ mm} = 10^{-3} \text{ m}$
Bước 2: Tính bước sóng $$\lambda = \frac{ia}{D} = \frac{10^{-3} \times 0.5 \times 10^{-3}}{1}$$ $$= 0.5 \times 10^{-6} \text{ m} = 5 \times 10^{-7} \text{ m}$$ $$= 500 \times 10^{-9} \text{ m} = 500 \text{ nm}$$
Bước 3: Xác định màu sắc
- $500 \text{ nm}$ nằm trong khoảng $500 – 570 \text{ nm}$
- Đây là ánh sáng lục (xanh lá cây)
Đáp số: Bước sóng $\lambda = 500 \text{ nm}$, ánh sáng màu lục (xanh lá).
Bài tập 5: Đếm số vân sáng
Đề bài: Trong thí nghiệm Young, khoảng vân $i = 0.4 \text{ mm}$. Trên màn quan sát có bề rộng $L = 8 \text{ mm}$ (đối xứng qua vân trung tâm). Hỏi trên màn có bao nhiêu vân sáng?
Lời giải:
Bước 1: Tính bán kính màn $$\frac{L}{2} = \frac{8}{2} = 4 \text{ mm}$$
Bước 2: Tính số vân sáng một bên $$k_{max} = \left[\frac{L/2}{i}\right] = \left[\frac{4}{0.4}\right] = [10] = 10$$
Bước 3: Tổng số vân sáng $$n_{sáng} = 2k_{max} + 1 = 2 \times 10 + 1 = 21$$
(Nhân 2 cho hai bên, cộng 1 cho vân trung tâm)
Đáp số: Có 21 vân sáng trên màn.
Bài tập 6: Xác định vân sáng hay vân tối
Đề bài: Trong thí nghiệm Young, khoảng vân $i = 0.5 \text{ mm}$. Tại điểm M cách vân trung tâm $x = 1.5 \text{ mm}$. Hỏi M là vân sáng hay vân tối bậc mấy?
Lời giải:
Tính tỉ số: $$\frac{x}{i} = \frac{1.5}{0.5} = 3$$
Vì kết quả là số nguyên (k = 3) → M là vân sáng bậc 3.
Đáp số: M là vân sáng bậc 3.
VIII. ỨNG DỤNG THỰC TẾ
1. Đo bước sóng ánh sáng
Phương pháp: Sử dụng thí nghiệm Young
- Đo khoảng vân $i$ (đo khoảng cách nhiều vân rồi chia trung bình)
- Đo khoảng cách hai khe $a$
- Đo khoảng cách đến màn $D$
- Tính $\lambda = \frac{ia}{D}$
Ưu điểm: Phương pháp đơn giản, chính xác cao, phổ biến trong phòng thí nghiệm.
2. Kiểm tra độ phẳng (Vân Newton)
Nguyên lý: Giao thoa trong lớp không khí mỏng giữa thấu kính và kính phẳng.
Hiện tượng: Xuất hiện các vân tròn đồng tâm.
Ứng dụng:
- Kiểm tra độ phẳng của bề mặt thấu kính
- Đánh giá chất lượng gia công quang học
3. Màng chống phản xạ
Nguyên lý: Phủ một lớp màng mỏng lên bề mặt thấu kính sao cho giao thoa giữa ánh sáng phản xạ từ hai mặt màng triệt tiêu nhau.
Điều kiện: Độ dày màng $d = \frac{\lambda}{4n}$ (với n là chiết suất màng)
Ứng dụng:
- Kính mắt chống phản xạ
- Ống kính máy ảnh
- Kính thiên văn, kính hiển vi
4. Holography (Ảnh ba chiều)
Nguyên lý: Ghi lại giao thoa giữa sóng vật và sóng tham chiếu từ laser.
Đặc điểm:
- Tạo ảnh 3D không cần kính đặc biệt
- Lưu trữ đầy đủ thông tin về biên độ và pha
Ứng dụng:
- Nghệ thuật, triển lãm
- Bảo mật (tem hologram trên tiền, thẻ)
- Y học, nghiên cứu khoa học
5. Màu sắc trên bong bóng xà phòng
Nguyên lý: Giao thoa ánh sáng trắng trong màng xà phòng mỏng.
Hiện tượng:
- Màu sắc thay đổi theo độ dày màng
- Các màu xen kẽ tạo hiệu ứng cầu vồng
Giải thích: Mỗi màu có bước sóng khác nhau → điều kiện giao thoa cực đại khác nhau → xuất hiện màu sắc khác nhau tại các vị trí khác nhau.
6. Giao thoa kế – Đo độ chính xác cực cao
Nguyên lý: Sử dụng giao thoa laser để đo khoảng cách.
Độ chính xác: Đến mức nanomét (nm = $10^{-9}$ m)
Ứng dụng:
- Đo độ dịch chuyển vi mô
- Phát hiện sóng hấp dẫn (LIGO)
- Kiểm tra kích thước linh kiện điện tử
- Đo độ biến dạng vật liệu
IX. KẾT LUẬN
Bài viết đã trình bày đầy đủ và chi tiết các công thức giao thoa sóng trong chương trình Vật lý lớp 12:
Giao thoa sóng cơ:
- Điều kiện cực đại: $d = k\lambda$
- Điều kiện cực tiểu: $d = (k+0.5)\lambda$
- Hiệu đường đi: $d = |d_1 – d_2|$
Giao thoa ánh sáng (Young):
- Khoảng vân: $i = \frac{\lambda D}{a}$
- Vị trí vân sáng: $x = ki$
- Vị trí vân tối: $x = (k+0.5)i$
- Bước sóng: $\lambda = \frac{ia}{D}$
Phân biệt hai loại giao thoa và các ứng dụng thực tế phong phú
Nguyên lý cơ bản cần nắm vững
Nguyên lý 1: Điều kiện giao thoa
- Hai nguồn phải cùng tần số và độ lệch pha không đổi (nguồn kết hợp)
Nguyên lý 2: Cực đại và cực tiểu
- Cực đại (vân sáng): Hiệu đường đi = số nguyên lần λ
- Cực tiểu (vân tối): Hiệu đường đi = số lẻ nửa λ
Nguyên lý 3: Khoảng vân
- Khoảng cách giữa hai vân sáng (hoặc hai vân tối) liên tiếp không đổi
- Bằng $i = \frac{\lambda D}{a}$
Lời khuyên học tập
📌 Học thuộc công thức cốt lõi: $i = \frac{\lambda D}{a}$ (quan trọng nhất)
📌 Phân biệt rõ sóng cơ và ánh sáng: Sóng cơ dùng hiệu đường đi $d$, ánh sáng dùng khoảng vân $i$
📌 Chú ý đổi đơn vị: Đặc biệt bước sóng từ nm → m
📌 Nhớ quy tắc vân sáng/tối:
- Vân sáng: k nguyên ($x = ki$)
- Vân tối: k + 0.5 ($x = (k+0.5)i$)
📌 Vân trung tâm: k = 0, LUÔN là vân sáng
📌 Luyện tập nhiều: Đặc biệt các dạng tính khoảng vân, vị trí vân, đếm số vân

Cô Trần Thị Bình
(Người kiểm duyệt, ra đề)
Chức vụ: Tổ trưởng chuyên môn Tổ Lý – Hóa – Sinh tại Edus
Trình độ: Cử nhân Sư phạm Vật lý, Hoá Học, Bằng Thạc sĩ, Chức danh nghề nghiệp Giáo viên THPT – Hạng II, Tin học ứng dụng cơ bản, Ngoại ngữ B1
Kinh nghiệm: 12+ năm kinh nghiệm tại Trường THPT Gia Định
